数学建模 停车距离问题教学过程

摘 要：数学建模是新课标中学科核心素养的一个重要部分，本文章主要是本人在上完一节数学建模课——“停车距离问题”之后进行反思与整理，将完整的教学过程及设计意图再一次进行展现。

关键词：数学建模;停车距离

一、 引入部分

（一）生活事故重现

开头语：很高兴来到温州育英和同学们一起来探讨数学问题，在座的有来自瑞安的同学吗？老师就是瑞安人，瑞安什么都好，就是有条隧道让我很不喜欢，每次回家经过老是堵车或发生事故，我们先通过一个视频一起感受下。

（二）观看视频

师：事故总是带来悲伤，相信大家都感到很惋惜，那我们怎么样可以减少或避免事故的发生呢？

刚才视频里有两段追尾的事故，大家觉得造成追尾的原因是什么呢？

注：抓住学生的回答，特别是有学生说到速度或距离的时候，如果都没有学生提出，就假装有。

生：速度太快，距离太近，那在一定的速度下，应该与前车保持多少距离才比较安全呢？

师：其实道路安全法有这么一条规定“当汽车行驶速度超过100公里/小时，与同车道前车距离要保持100米以上”。同学们觉得这100米是否合理呢？这节课我们就带着这个问题来研究下行车距离问题。

（三）引出课题

注：板书跟上“停车距离问题”。

二、 确定变量

（一）影响因素分析

师：影响行车距离的因素有哪些呢？板书影响因素。

注：口头提问，学生一起回答，板书记录关键因素，如速度、反应时间、摩擦力、制动力、空气阻力等。

师：大家觉得影响行车距离的最关键因素是什么？

师：今天我们就主要研究距离与速度之间的关系，那其他影响我们做如何处理呢？

师：很好，控制变量法，假设其他影响因素保持不变。

用红色粉笔圈出速度。

三、 建构模型

连接语：从刚才同学们对影响因素的分析中，我们大概也了解了汽车停止前的运动状态，大家看屏幕，一开始司机会有个反应阶段，对应的距离我们称为反应距离，接下来开始减速，对应的距离称为制动距离，合起来我们称停车距离。

问题1：在这样的运动状态下，能否建立距离d与速度v的函数关系式？

连接语：通过理论分析我们得到了距离d与速度v是一个二次关系，那我们现在可以解决开始的这个问题了吗？（反应时间和加速度不知道）很好，对不同的人，不同的环境，它们都是不一样的，那我们该怎么去估算它们呢？（数据，试验，调查）

很好，老师这里刚好有一组公路局公布的试验数据，大家请看屏幕。（介绍表格内容）请同学们根据这组数据，来估算α，β。

1～2分钟交流沟通，下去指导。

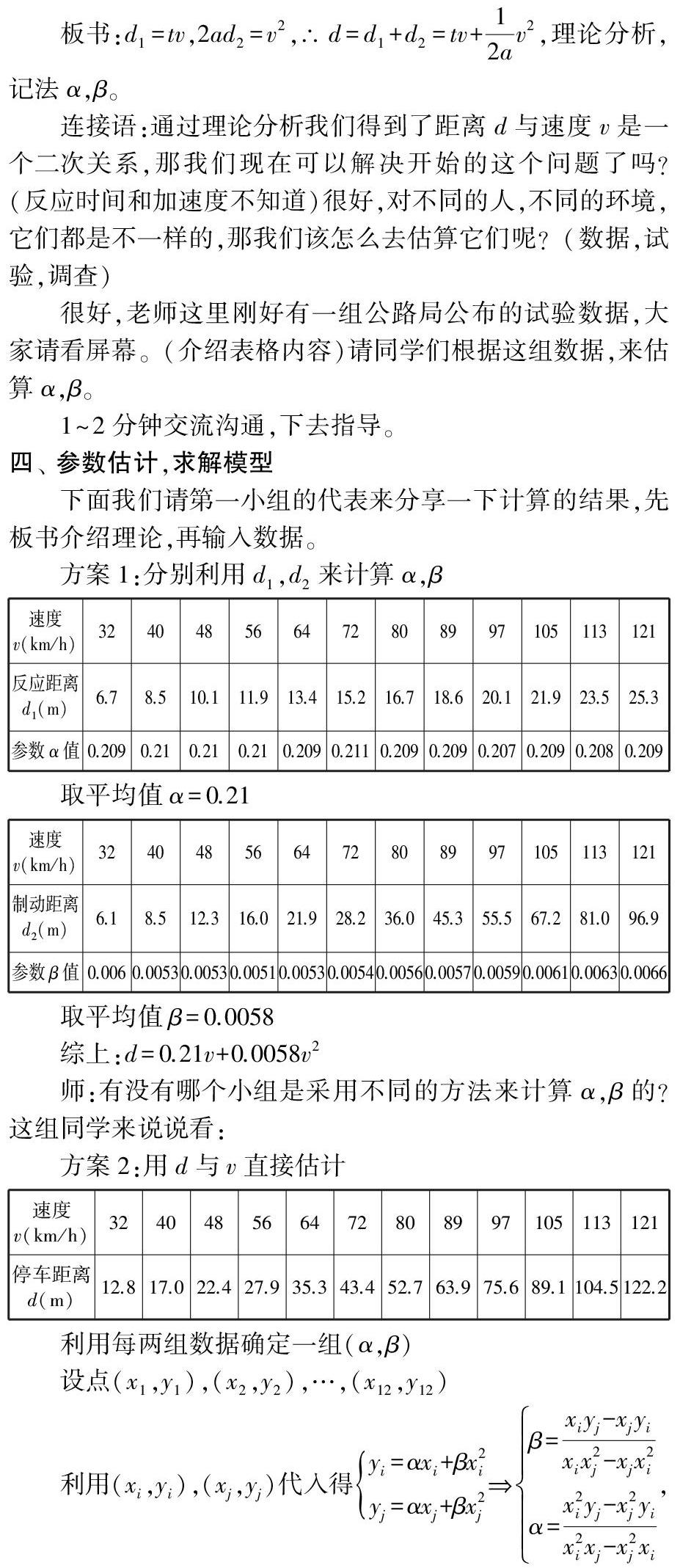
四、 参数估计，求解模型

下面我们请第一小组的代表来分享一下计算的结果，先板书介绍理论，再输入数据。

连接语：通过两种不同的参数估计方法，我们得到了两个不同的模型，现在我们能解决开始的那个问题了吗？

关键问题①80米离100米还有20米空间，为什么留这么长？

关键问题②100米真的够吗？你们就这么相信这两个模型啊，就不怕它们有大的误差吗？

师：那我们还是把模型算出来的值与真实试验值做下对比吧。

师：根据模型，应该说对100的预测应该还是比较准的，大家建构的模型很棒，为自己鼓鼓掌吧。

关键问题③现在路上超速驾驶的司机也常有，我们再利用模型预测一个吧，比如速度为128km/h，大家快速算一下。

师：两个模型分别是121.8和125.4，你们觉得保持多少距离比较安全啊？

师：其实老师一开始保留了一个公路局公布的数据，真实试验值多少呢？是141.4。

师：误差有点大，大家可以再看看这两个模型，速度比较小时，模型值与真实值是比较接近的，速度比较大时，误差似乎大起来了，那大家觉得这两个模型还适合用于高速的预测吗？

师：那你能否构建新的模型使得对低速与高速的预测误差都相对较小呢？

关键问题④要寻找新模型，首先我们肯定要先了解误差的来源，大家觉得为什么会有误差呢？

师：很好，模型的构建是基于理想化运动状态得到的;参数估计方法不同误差也会不同。

师：那我们就先从参数估计方法入手，大家觉得对高速的预测哪个模型可能会更好一点？

师：那我们就从这里入手，大家看导学单2，看数据特点，看能不能得到一些启发。

注：误差产生原因①模型本身是在理想化运动状态下得出来的;②参数估计不同也会有误差。

五、 优化模型

小组讨论，学生分享。

（一）调整参数估计方法

师：从数据上看，当选的组号比较大时，预测值比较大，组号比较小时，预测值比较小，我们组把数据分成两组，前六个为一组，后六个为一组，再通方案2方式分别估计出两组（α，β），进而得到两个模型。

师：看Excel表格，到此为止，我们通过不同的参数估计方法得到了3个模型，现在我们把数据通过图像呈现出来，让大家更加直观地感受下。

确实，模型3能相对精确的对低速和高速进行预测。

（二）调整模型类型

连接语：以上是根据数据的特点，通过调整参数估计方法来优化模型。我们再看刚才分析的误差产生的第二个原因，得到的模型是基于理想化运动状态，那我们看这个式子d=tv+12av2，在实际生活中，t和a一定是和v无关的常数吗？如果不是，那d与v还一定会是二次吗？那我们能否抛开理论，直接从数据出发重新去构建模型呢？

师：大家看数据，我们一般都是怎么样利用数据来判断两个量之间可能存在的函数关系的？好，那大家在坐标系下把点描描看，看有什么新的想法？

六、 总结

同学们，接下来我们来总结下这节课的内容，本节课我们是从一個实际情景里抽象出一个数学问题，然后通过分析影响因素确定了主要变量，然后先是从理论角度建构模型，再利用数据估算参数求解模型，然后解决问题，但在问题的解决过程中我们又发现了模型的不足，所以又通过细化数据改变参数估计方式优化模型，同时，我们又抛开理论直接从数据本身出发重新建构了新的模型，已达到我们的要求。这其实就是一个数学建模的过程。在整个建模的过程中，我们不禁会思考我们得到了这么多模型，到底哪个好，其实每个模型都有误差，但也都有它的价值，模型只有在一定条件下才是好模型，这也正如一位统计学家所说“all modles are wrong， but some modles are useful”。

参考文献：

[1]史宁中，王尚志.普通高中数学课程标准（2017版）解读[M].北京：高等教育出版社，2018.

作者简介：

杨云飞，浙江省温州市，浙江省温州中学。