一类不稳定时滞过程的内模控制器设计方法
2020-05-29刘立业
刘立业
(石家庄职业技术学院 电气与电子工程系,河北 石家庄 050081)
0 引言
时滞过程广泛存在于各种控制系统中,例如电力系统、气动与液压网络系统、化工控制过程系统、机器人控制系统等.时滞过程主要是由质量、能量和信息等各种物理信号传输的延时造成的,但也有些是由信号处理过程或误差累积引起的.其中,部分时滞系统不稳定且具有积分过程,例如水泵控制、液体储存器、连续搅拌反应釜、蒸馏塔等过程. 无论是在控制过程中还是在系统的内部状态中,时滞过程都会引起控制系统的消极动态响应,甚至不稳定.因此,不稳定时滞过程的控制能力、观测能力、鲁棒性、系统优化、自适应控制、极点配置、稳定性能分析和鲁棒稳定性等问题,引起了越来越多研究人员的关注.文献[1]提出了一种改进型的史密斯预测控制,主要用于不稳定时滞系统的控制,其核心思想是通过将基于线性二次型的最优控制引入到史密斯预测控制结构中,来改进不稳定时滞过程控制系统的动态性能.文献[2]研究了各种不同的不稳定时滞过程的动态特性,提出了一种基于直接分析法的改进PID(Proportional-Integral-Derivative)控制器的设计方法,通过仿真实验分析了不稳定时滞过程控制系统的超调量、响应时间、最大灵敏度等时域性能指标的变化特性,并验证了此方法的有效性.文献[3]利用主动抗干扰控制技术分析了不稳定时滞过程的动态特性,提出了一种二自由度的控制结构,用于分别控制系统的定值跟踪响应和抗干扰响应.这种控制结构的主要特点是利用控制系统所有的已知信息来整定主动抗干扰的控制器参数,并通过分析控制系统的鲁棒性和动态性能来验证方法的有效性.此外,一些新型的有关处理时滞过程的算法也正在研究中[4-5].
由于不稳定时滞过程的处理技术具有很强的工程实践意义,因此不稳定时滞过程相关控制技术的研究始终是科研和工程技术人员的研究热点和关注点.本文通过对不稳定时滞过程的零极点特性的分析,提出一种基于内模控制(Internal Model Control,简写为IMC)的不稳定时滞过程的控制方法.
1 问题描述
根据位于右半平面极点(Right Half Pole,简写为RHP)的个数,低阶不稳定时滞过程分为单极点不稳定时滞过程、双极点不稳定时滞过程和震荡不稳定时滞过程.为了便于讨论不稳定时滞过程的时域特性,本文选取一阶(单极点)不稳定时滞过程为研究对象.一阶不稳定时滞过程的传递函数如公式(1)所示.
(1)
公式(1)中,K表示增益,T表示时间常数,e-τs表示时滞过程,τ表示时滞时间,s表示拉普拉斯算子.由公式(1)可以分析出一阶不稳定时滞过程的主要特点,即具有一个右半平面极点1/T,如图1所示.
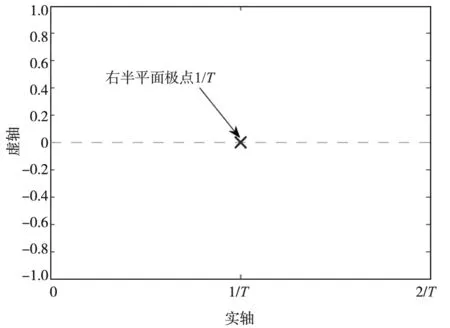
图1 一阶不稳定时滞系统的零极点图
由劳斯判据可知,系统稳定的充要条件是系统的所有极点必须位于左半平面,即特征方程的根必须具有负实部[6].由此可以判定,由公式(1)所表示的对象过程是开环不稳定的.图2为一阶不稳定时滞过程的开环单位阶跃响应曲线.分析曲线的时域性能可知,响应曲线的幅值呈指数增长,系统的动态性能指标均不满足要求,系统发散不可控.
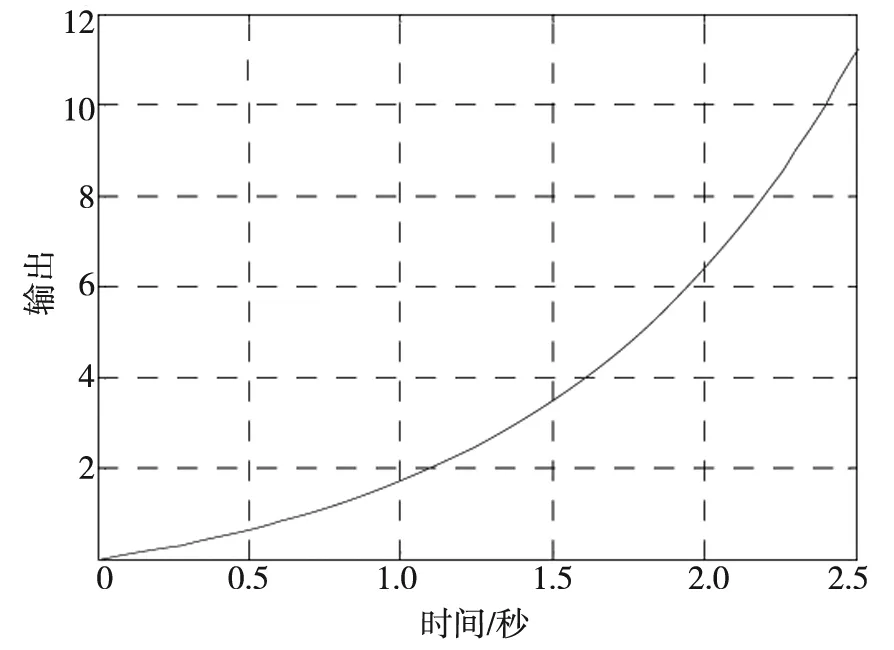
图2 一阶不稳定时滞过程的开环单位阶跃响应输出曲线
2 不稳定时滞对象的内模控制方法
根据分析得出的一阶不稳定时滞过程的时域特性,利用内模控制处理时滞环节的优势,通过设计合理的内模控制器的低通滤波器的结构与参数,来消除不稳定时滞过程的右半平面极点的消极影响.本文所设计的内模控制系统的结构示意图如图3所示.

图3 内模控制系统结构示意图
图3中,r(s),y(s)和d(s)分别表示一阶不稳定时滞对象控制系统的定值输入、响应输出和内部干扰量;Q(s),G(s)和Gm(s)分别表示一阶不稳定时滞对象控制系统的内模控制器、被控对象和匹配模型;s为拉普拉斯算子;R(s)表示等效反馈控制器.
由内模控制原理[7]可知,内模控制器的设计过程可以分为两步.
第一步,首先将被控对象分解成两部分,如(2)式所示.
Gm(s)=Gm+(s)Gm-(s).
(2)

第二步,由第一步分析可得,在内模控制器中引入低通滤波器后的公式如(3)所示.

(3)
(3)式中,

(4)
其中,在低通滤波器F(s)中,阶次n表示低通滤波器的阶数,阶次n的值为能够使内模控制器Q(s)真有理且可实现的最小数值,由于本文的研究对象为一阶不稳定带时滞过程,因此,二阶低通滤波就可以满足系统的鲁棒性要求,即n=2;λ表示时间常数,它是影响控制器性能的重要指标;α表示低通滤波器的零点,其设立的目的是为了消除不稳定时滞对象的右半平面极点对系统的影响.
当被控对象为公式(1)所示的对象时,由公式(2)至公式(4)可得其内模控制器的表达式为:
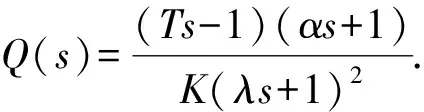
(5)
由图(3)可知,其等效反馈控制器的表达式如式(6)所示.
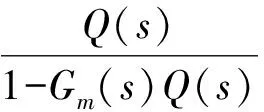

(6)
由公式(6)可知,等效反馈控制器的特征方程含有被控对象的右半平面极点.为消除其对控制系统的影响,应充分设计参数α,根据终值定理,可得公式(7).
(7)
由于公式(7)含有时滞项,不容易求α的解析解,因此采用一阶泰勒近似法处理时滞项,得(8)式.
e-τs≈1-τs.
(8)
将公式(8)代入公式(7),可得
(9)
化简求解可得α与λ的关系表达式,如公式(10)所示.
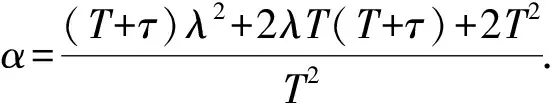
(10)
将公式(10)代入公式(6)中,可得到等效反馈控制器R(s)的解析表达式,进而可得到一阶不稳定时滞内模控制系统的开环传递函数P(s)的解析式,如公式(11)所示.
P(s)=G(s)·R(s)=
(11)
其中,β=(T+τ)λ2+2λT(T+τ)+2T2.
由一阶不稳定时滞内模控制系统的开环传递函数P(s)的解析式可以看出,在加入控制器后,原控制系统中的右半平面极点被抵消,这就消除了右半平面极点对控制系统稳定性的影响.
3 仿真结果与时域分析
针对公式(1)所给出的一阶不稳定时滞对象,为了便于计算并分析其结果,令T=2,K=1,τ=2,λ=0.5,则根据公式(10)可以求出α=14;将所有参数代入公式(5),可以得出该被控对象的内模控制器Q(s)的解析表达式,如(12)式所示.
(12)
与图1比较,一阶不稳定时滞过程实施内模控制前后的零极点变化情况如图4所示.

图4 一阶不稳定时滞过程内模控制系统零极点图
由图4可知,实施内模控制后一阶不稳定时滞过程具有两个共轭负极点和一个不影响系统动态性能的右半平面零点,而右半平面极点1/T已被抵消,因此,控制系统的动态性能满足稳定条件.
图5为不同时滞条件下一阶不稳定时滞过程的内模控制系统响应曲线.

图5 不同时滞条件下一阶不稳定时滞过程的内模控制系统响应曲线
从图5可以看出,单位阶跃输入响应内模控制系统分别在时滞时间增大5%,15%和25%时的输出响应曲线.分析输出曲线图可知,当系统模型误差较小时,不会对系统的动态性能造成严重影响;随着误差逐渐增大,控制系统的动态性能受到的影响也越来越大.
不同时滞条件下一阶不稳定时滞过程的内模控制系统的动态性能指标如表1所示.
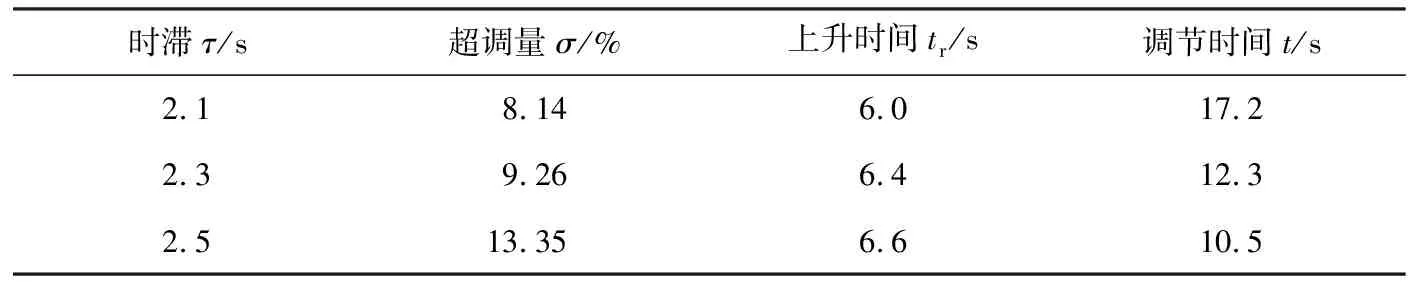
表1 不同时滞条件下一阶不稳定时滞过程的内模控制系统的动态性能指标
由表1可知,当不稳定时滞过程控制系统的时滞逐渐加大时,超调量变大,上升时间变化不明显,调节时间逐渐变小.这说明,不稳定时滞过程的内模控制系统能有效地抑制时滞过程对系统的影响.
4 结论
(1)本文所提出的控制方法适用于低阶不稳定时滞过程.高阶不稳定过程需要进行降阶处理后,再应用本文所提出的控制方法.
(2)通过设计内模控制中低通滤波器的结构和参数可以实现不稳定时滞过程的稳定控制.
(3)仿真结果表明,一阶不稳定时滞过程的内模控制系统的超调量明显增加时,上升时间相对变化不明显,调节时间明显变短,系统的动态性能指标能够满足控制系统的要求.
