大质量中子星可包含超子

王 红 岩

(北华大学 理学院, 吉林 吉林 132013)

中子星是宇宙中最致密的物质, 由于密度极高的物质不能在实验室制备, 因此对其内部极高密度下物质存在形态的认识具有极大不确定性[1].由致密物质组成的星体是传统中子星、超子星、夸克星或混合星取决于其内部结构.文献[2-4]通过天文观测发现了约2M⊙(M⊙为太阳质量,M⊙=1.989×1030kg)的中子星PSR J0348+0432((2.01±0.04)M⊙)和PSR J1614-2230((1.97±0.04)M⊙).由于构成大质量中子星内部的状态方程需足够硬, 因此已引起人们广泛关注[4-6], 双中子星系统中单个星体的质量约为(0.86～2.26)M⊙, 合并后的质量约为2.7M⊙[6-8].

平均场理论可用于描述中子星结构及中子星状态方程和质量半径的关系[9-13].将中子星的最大质量和相应半径的理论计算值与天文观测数据对照, 可确定中子星的合理相结构.理论计算表明, 仅含核子相结构的状态方程导致中子星的最大质量可达2M⊙[14-15].在考虑超子自由度后, 中子星的状态方程变软, 最大质量减小(约1.5M⊙), 与天文观测的小质量中子星((1.4～1.6)M⊙)一致[16-18].在观测到中子星PSR J1614-2230和PSR J0348+0432及双中子星合并GW170817后, 由于质量较大(约2M⊙)， 因此排除了超子相.在足够硬的核子状态方程引入超子自由度后, 其质量降低, 但不一定均小于2M⊙, 即大质量中子星可排除一部分传统中子星模型.中子星的最大质量由状态方程确定, 而状态方程的软硬程度依赖于平均场理论下核子参数组的选择[19].

为研究大质量中子星的相结构, 本文利用平均场理论, 用7个参数组(NLSH,NL3,NL2,GL1,GL2,GL3,GL85)计算有无超子两种情形下的状态方程和质量半径关系, 并分析超子耦合常数χ对中子星质量的影响.通过状态方程及超子耦合常数研究大质量中子星中存在超子相的可能性[20].

1 理论模型及计算公式

利用相对论平均场理论(RMFT)研究强子层次大质量中子星的结构和性质.在RMFT下处于β平衡强子物质的Lagrange密度[21]为

其中B表示重子八重态n,p,Λ,Σ-,Σ0,Σ+,Ξ-,Ξ0.在平均场近似中, 由式(1)可得强子和介子的运动方程.自洽求解强子和介子的运动方程、β平衡条件及电荷中性条件, 最后得到奇异强子物质中子星的能量密度和压强分别为

由能量密度和压强即可出中子星的状态方程.

利用中子星结构广义相对论静态流体力学Tolman-Oppenheimer-Volkoff(TOV)方程[9]可求解中子星的质量和半径关系为

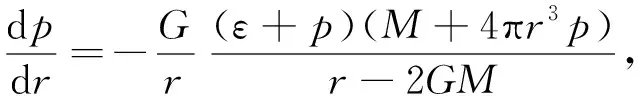
(4)

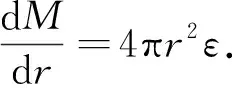
(5)

将状态方程作为输入量, 求解TOV方程, 即可得中子星的质量和半径关系为

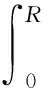
(6)

在相对论平均场理论中, 重子通过交换标量介子和矢量介子相互作用, 介子-核子间存在相互耦合作用(gσN,gωN,gρN), 超子-介子间也存在相互耦合作用(gσH,gωH,gρH).定义超子-介子耦合常数与核子-介子耦合常数的比为超子(相对)耦合常数[15,21]：

且令χσ=χω=χρ=χ.本文选取超子耦合常数χ=0.4～1.0, 研究χ对状态方程和质量半径关系的影响.

2 结果与讨论

利用相对论平均场理论, 用7个参数组(NLSH,NL3,NL2,GL1,GL2,GL3,GL85)计算状态方程和质量半径的关系, 研究不同参数组对中子星质量的影响, 并对有无超子两种情形进行对比.7个参数组得到的中子星状态方程如图1所示; 7个参数组得到中子星质量和半径的关系如图2所示.其中 阴影区为J1614-2230和J0348+0432的脉冲星带, 黑点为中子星的最大质量.由图1和图2可见, 不同核子参数组对中子星的质量和半径均有影响.用3个参数组NLSH,NL3，NL2计算得到的状态方程相对较硬, 质量相对较大, 其中用NLSH参数组计算得到的质量最大, 状态方程最硬.用4个参数组GL1,GL85,GL2，GL3得到的状态方程相对较软, 质量相对较小.用7个参数组计算得到的质量均大于等于2M⊙, 即在J1614-2230和J0348+0432脉冲星带及以上.

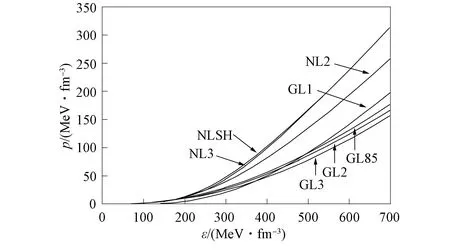
图1 7个参数组得到的中子星状态方程Fig.1 Equations of state of neutron star obtained by seven parameter sets

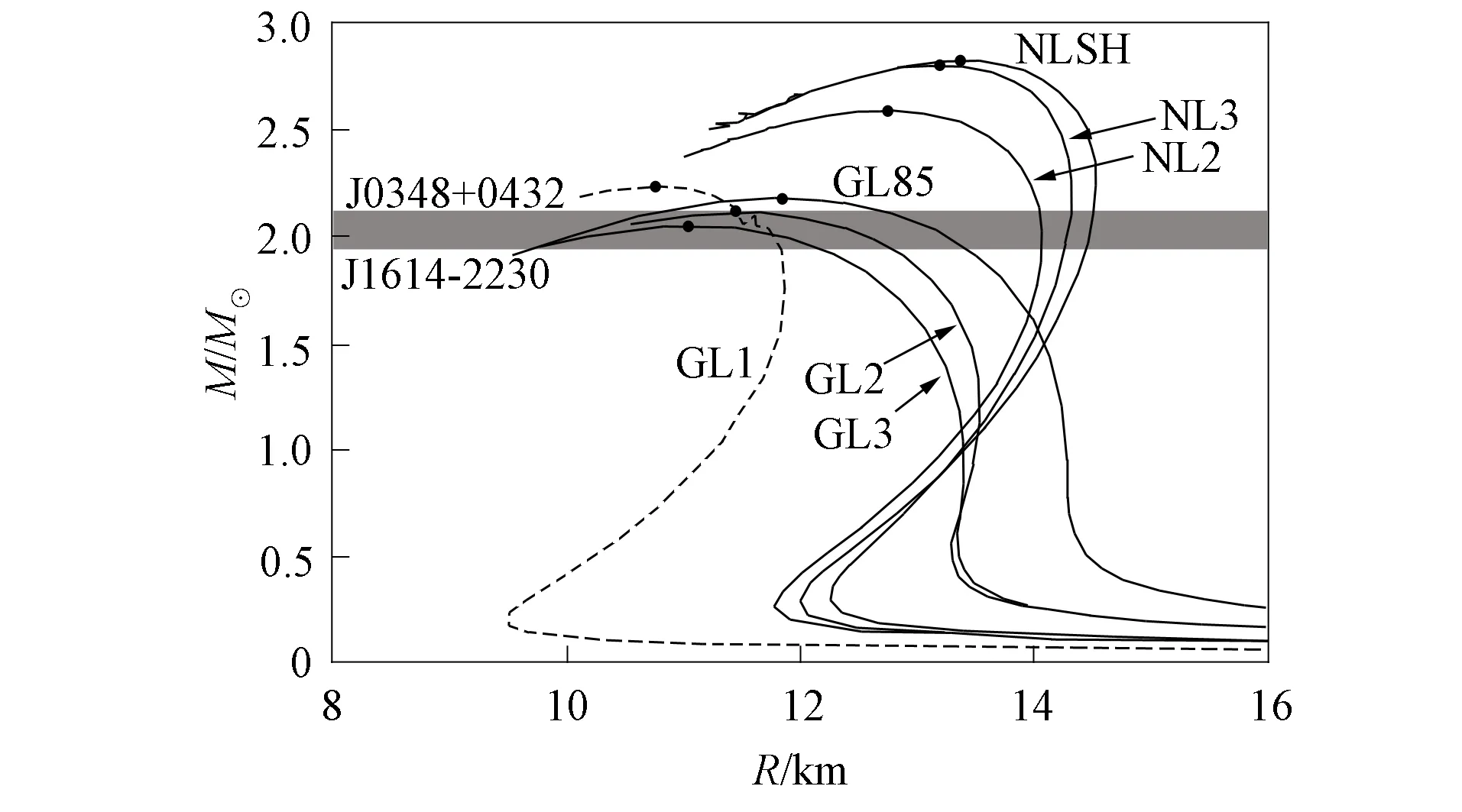
图2 7个参数组得到中子星质量和半径的关系Fig.2 Mass-radius relationship of neutron star obtained by seven parameter sets

考虑超子并选取超子耦合常数χ=1.0, 用7个参数组给出质量和半径的关系, 结果如图3所示, 其中黑点为中子星的最大质量.比较图2和图3可见, 超子降低了中子星的最大质量, 与理论计算结果相符, 但7个参数组的结果差别较大, 与3个相对较硬状态方程对应的中子星最大质量均大于2M⊙, 即均在J1614-2230和J0348+0432脉冲星带以上, 与4个相对较软状态方程对应的中子星最大质量均小于2M⊙, 即均在J1614-2230和J0348+0432脉冲星带以下.表明大质量中子星可存在超子相, 由参数组状态方程的相对硬度决定.

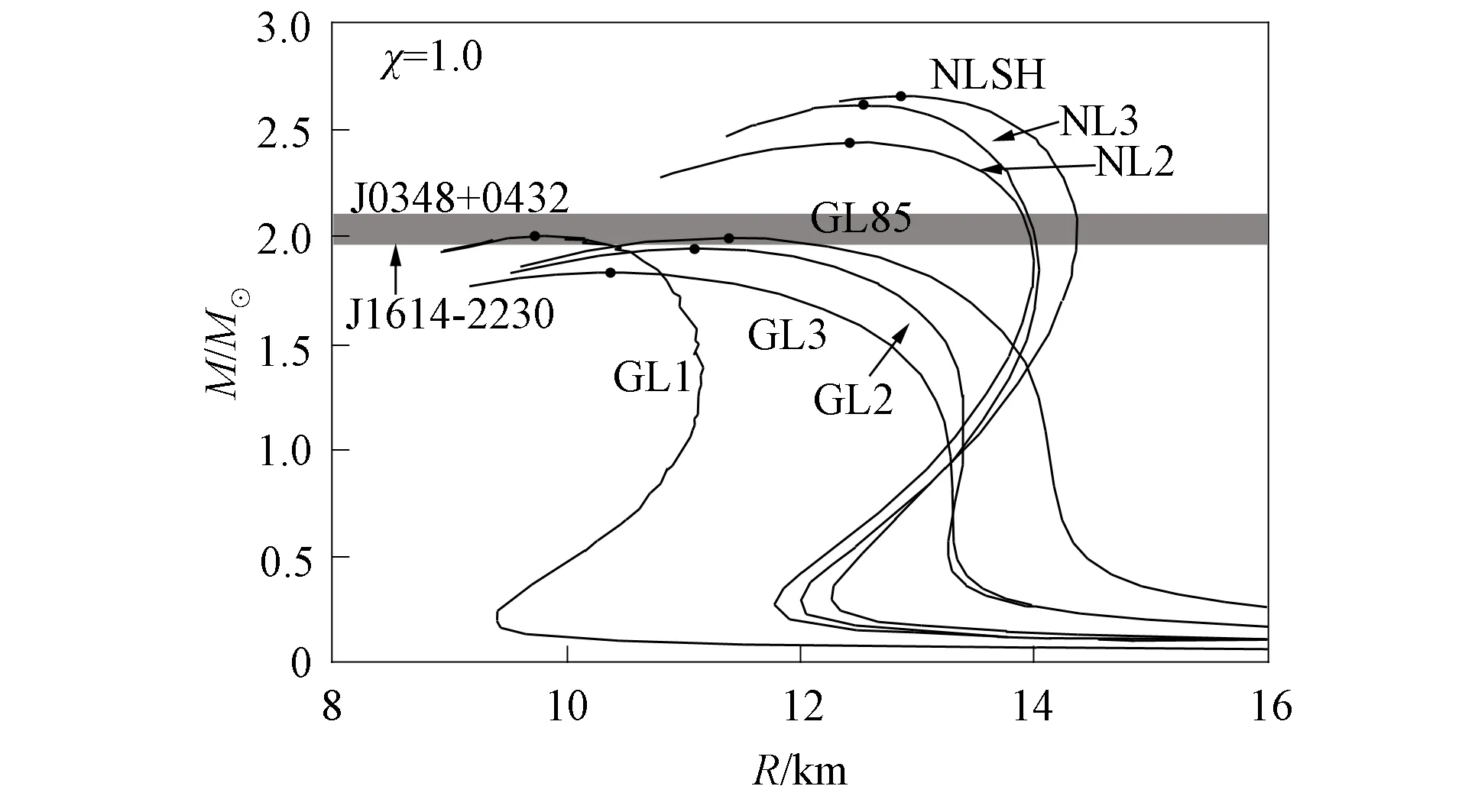
图3 7个参数组在χ=1.0时得到 中子星质量和半径的关系Fig.3 Mass-radius relationship of neutron star obtained by seven parameter sets at χ=1.0

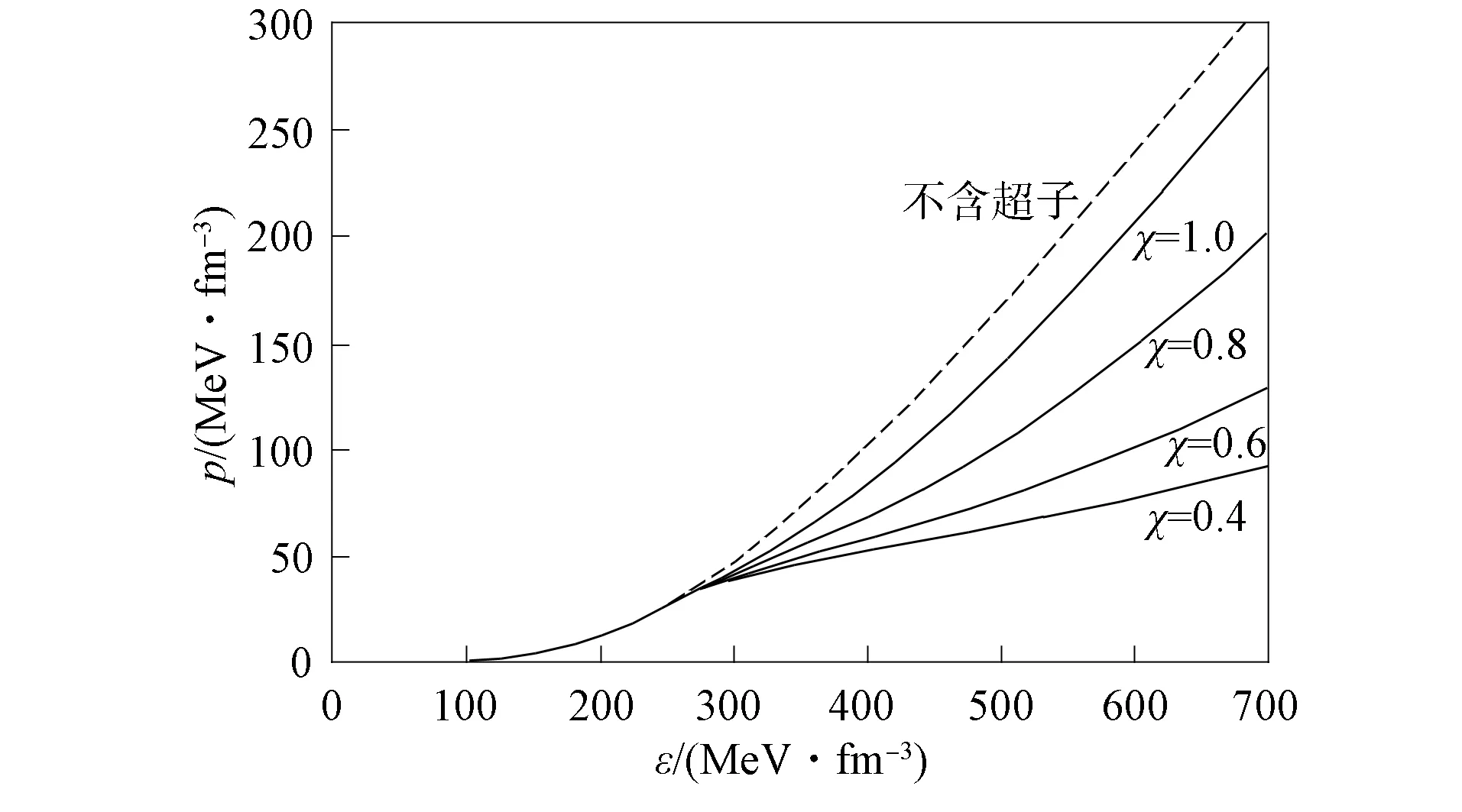
图4 NLSH参数组在不同超子耦合 常数下的中子星状态方程Fig.4 Equations of state of neutron star for NLSH parameter set with coupling constants of hyperons

NLSH参数组在不同超子耦合常数下的中子星状态方程如图4所示.NLSH参数组在不同超子耦合常数下中子星质量和半径的关系如图5所示； GL85参数组在不同超子耦合常数下中子星质量和半径的关系如图6所示.其中阴影区为J1614-2230和J0348+0432的脉冲星带.由图4～图6可见: 随着超子耦合常数的增大, 中子星的状态方程变硬, 最大质量变大, 半径减小； NLSH参数组在χ≥0.6下获得了大质量中子星, 质量在J1614-2230和J0348+0432脉冲星带以上; GL85参数组仅在χ=1.0下得到大质量中子星, 即大质量中子星的最大质量依赖于超子耦合常数.在状态方程相对较硬的条件下, 选择强耦合常数可得到大质量的中子星, 因此大质量中子星可包含超子相.

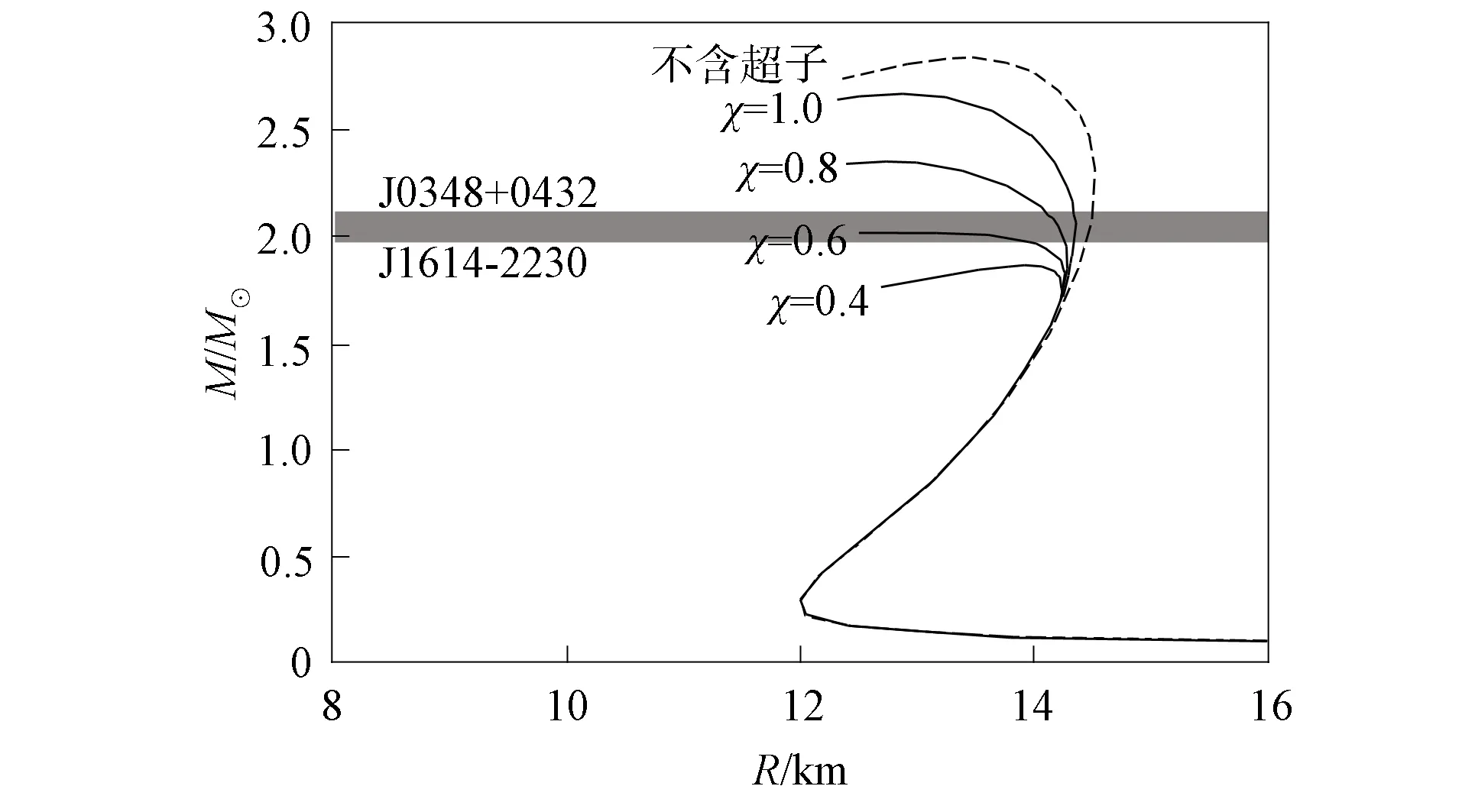
图5 NLSH参数组在不同超子耦合 常数下中子星质量和半径的关系Fig.5 Mass-radius relationship of neutron star for NLSH parameter set with coupling constants of hyperons

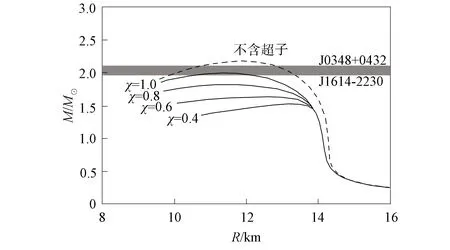
图6 GL85参数组在不同超子耦合 常数下中子星质量和半径的关系Fig.6 Mass-radius relationship of neutron star for GL85 parameter set with coupling constants of hyperons

综上所述, 本文研究了大质量中子星状态方程和质量半径的关系.结果表明: 用7个参数组均可获得大于2M⊙的中子星, 按状态方程的软硬程度可分为状态方程较硬(NLSH,NL3,NL2)和状态方程较软(GL1,GL85,GL2,GL3)两组; 在考虑超子自由度后, 用较硬状态方程计算得到的中子星最大质量仍大于2M⊙, 用较软状态方程计算得到的中子星最大质量小于2M⊙, 即大质量中子星依赖于参数组； 随着χ的增强, 中子星的状态方程变硬, 最大质量变大; NLSH参数组当χ≥0.6时获得了大质量中子星, GL85参数组仅在χ=1.0时得到大质量中子星, 即大质量中子星可包含超子, 但依赖于超子耦合常数的强弱.因此选择硬的状态方程和强超子耦合常数可获得大质量中子星.