一类非Newton流方程整体解的存在唯一性
2020-05-29徐建军袁洪君
徐建军, 袁洪君
(吉林大学 数学学院, 长春 130012)
0 引 言
目前, 关于可压缩Navier-Stokes方程整体解的研究已取得了很多成果: Matsumura等[1]证明了三维可压缩Navier-Stokes方程初值在某个平衡态附近小扰动时整体强解的存在唯一性, 并得到了解的长时间性态; Hoff[2-3]得到了小能量情形下二(三)维可压缩等熵Navier-Stokes方程整体弱解的存在性; Lions[4]在绝热指数γ适当大的条件下(当维数N=2时要求γ≥3/2, 当维数N=3时要求γ≥9/5), 利用弱收敛方法得到了弱解的整体存在性, Feireisl等[5]将其推广到γ≥N/2的情形; Wang等[6]采用迭代的方法研究了一类密度较小且初始值满足相容性条件的非Newton流体方程, 得到了其整体强解的存在唯一性; Huang等[7]证明了一类初始密度含真空的等熵Navier-Stokes方程Cauchy问题小能量整体古典解的存在性; Huang等[8]研究了一类小能量三维可压缩Navier-Stokes方程, 在初始值光滑时, 得到了其经典解的存在唯一性, 在初始值不连续的情形下, 得到了其整体弱解的存在性; Fang等[9]利用能量估计及迭代的技巧证明了一类具有大初值的非Newton流方程经典解的整体存在唯一性; Yuan等[10]证明了一类初始密度含真空的Navier-Stokes方程Cauchy问题小能量整体强解的存在唯一性, 并研究了解的长时间性态.
本文考虑如下一维带外力项的可压缩非Newton流体方程:
具有初边值条件
其中: 未知函数ρ=ρ(x,t),u=u(x,t),π(ρ)=aργ(a>0,γ>1)和f=f(x,t,u)分别被定义为密度、速度、压力和外力;Ω∶=(0,1);p∈(5/3,2); 初始密度ρ0≥0.
1 主要结果
函数f=f(x,t,y)∈C1([0,1]×[0,+∞)×(-∞,+∞))满足如下条件:

本文在外力f满足条件(5)-(7)的情形下证明如下结果:
定理1假设5/3 (8) 和相容性条件 (9) 并且有如下长时间行为: (10) 整体存在性(即定理1)主要通过对局部解的整体估计得到, 故这里给出问题(1)-(4)局部强解的结果[11]. 对于初边值问题(1)-(4), 下面给出先验估计.令T>0为固定时间, (ρ,u)为问题(1)-(4)在Ω×(0,T]上的光滑解, 其中问题(1)-(4)的初始值(ρ0,u0)满足条件(8)-(9). 为方便, 定义一些简化符号如下: 其中: 1≤p≤∞;k∈. 引理1假设(ρ,u)为初边值问题(1)-(4)在Ω×(0,T]上的光滑解, 则有 (11) 其中C0为常数. 引理1的证明类似于文献[10], 故略. 对Ω×(0,T]上初边值问题(1)-(4)的光滑解, 当5/3 (12) (13) (14) 其中m1,m2均为正常数, 则在假设E0≤ε及σ(t)∶=min{1,t}的条件下, 如下估计成立: (15) (16) (17) 证明: 分四步证明. 1)ux的Lp-范数估计. 首先利用式(1), 将式(2)化为 (18) (19) 利用分部积分、u|∂Ω=0及边界条件(4)可得 (20) 再次利用分部积分、式(1)以及边界条件ut|∂Ω=0, 有 (21) 将式(20),(21)代入式(19), 有 先对式(18)两边同乘以u, 并作用∂x, 有 (23) 然后对方程(18)作用 ∂t, 可知 (24) 将式(23),(24)相加, 并处理右端项, 有 (25) 将式(26)两端乘以σm2, 并关于x在Ω上积分, 利用分部积分及Cauchy-Schwarz不等式, 可得 3) ‖ux‖∞的估计及式(15),(16)的证明. 令 (28) 则由式(1)知 (29) 由式(28),(29)直接可推得 (30) (31) (32) 从而 (33) 因此, 由F的定义式(28)可知 (34) 由积分中值定理, 在区间(0,1)中存在一点ξ, 使得 从而有 (35) 利用式(30)~(32),(35), 由Hölder不等式及Cauchy-Schwarz不等式, 有 (36) 由式(36)可得 将式(37)代入式(22), 并关于时间在[0,t]上积分, 利用式(11)~(13)、m1≥1及(3p-3)m1≥m2, 可得 又由于 (39) (40) 故由式(36)及式(11)~(13), 可知 从而有 由式(36)可得 从而有 4) ‖ρ‖∞的估计. 引理2(Zlotnik不等式) 假设函数y满足 Dty(t)≤f(y)+Dtb(t)于[0,T],y(0)=y0, (44) 其中:f∈C();y,b∈W1,1(0,T).如果f(∞)=-∞, 且 |b(t2)-b(t1)|≤N0+N1(t2-t1) 对所有的0≤t1 引理2的证明类似于文献[12]中引理1.3的证明, 故略. 引理3的证明参见文献[10]. 由式(1)知 Dtρ≤-ρux, (45) 其中Dtρ=ρt+ρxu. 利用式(44)处理-ρux, 由式(45)、引理2和引理3, 可得 (46) 考虑如下两种情形. 情形① 0 (47) 由式(47)联立式(36), 可得 由m1+m2<3p-2且5/3 且有 利用式(48),(49), 有 (50) 情形②σ(T) 在该情形下, 通过计算有 其中当σ(T) (51) 进一步有 取N1和N0如下: 注意到 至此, 命题2证毕. 考虑解(ρ,u)的高阶导估计, 类似文献[10]中的证明方法可得如下结果: 引理4如下不等式成立: 根据命题1知, 存在T*>0, 使得初边值问题(1)-(4)在Ω×(0,T*]上有唯一的强解(ρ,u).由先验估计、命题2和引理4可将局部强解(ρ,u)延拓到全局.由式(8)可知, 存在T1∈(0,T*], 使得式(12)~(14)对T=T1成立.令 T*=sup{T|式(12)~(14)成立}. (52) 对任意0<τ (53) 为证明式(10), 将方程(1)两端乘以aγργ-1, 有 πt+uπx+γπux=0. (54) 将式(54)与qπq-1在Ω×(1,∞)上做内积可得 (55) (57) (58) 把式(56)~(58)代入式(55), 可知 (59) 下面给出速度的衰减估计, 借助式(36),(16),(17), 有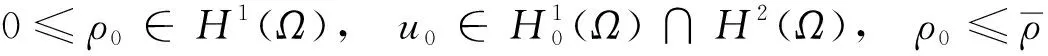
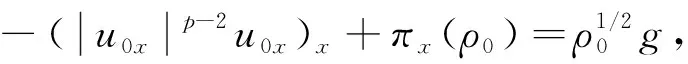
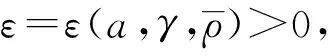


1.1 先验估计

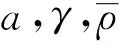
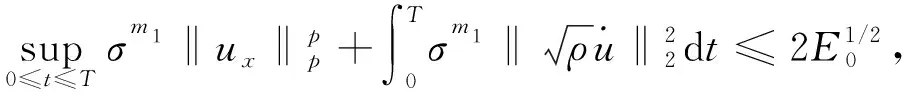
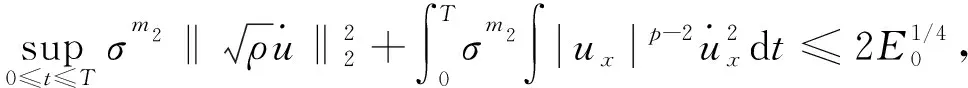


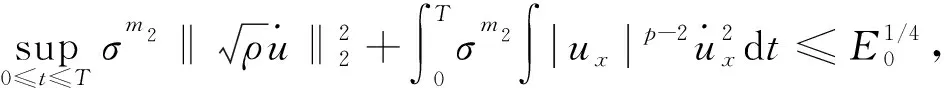



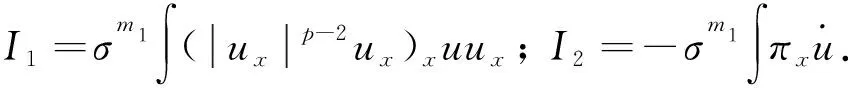

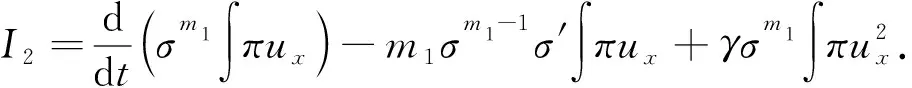
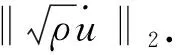


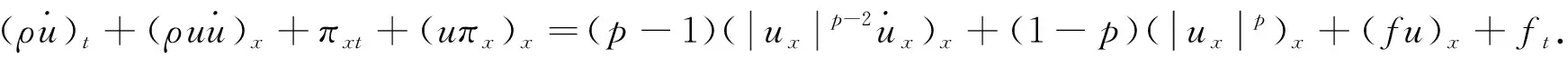

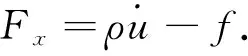
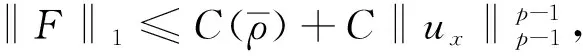
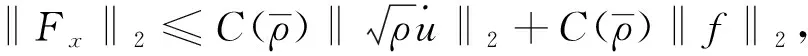
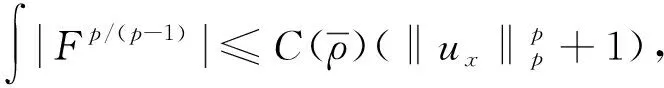

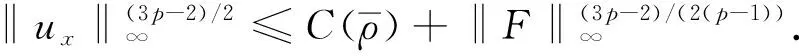
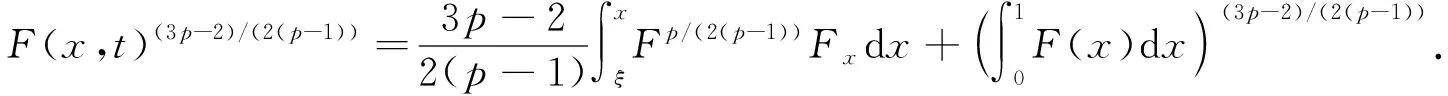

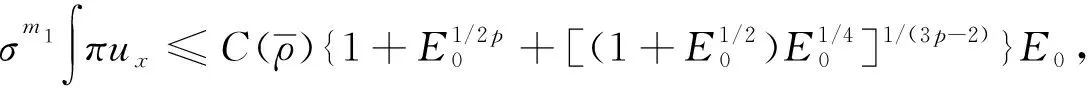
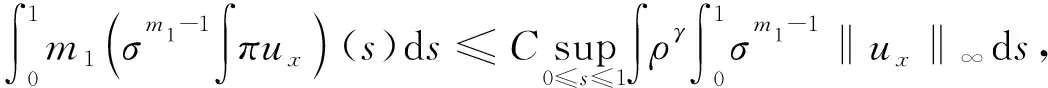
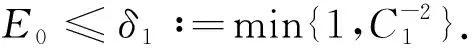
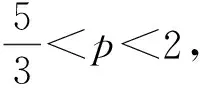
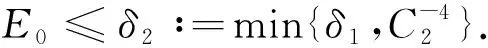

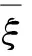

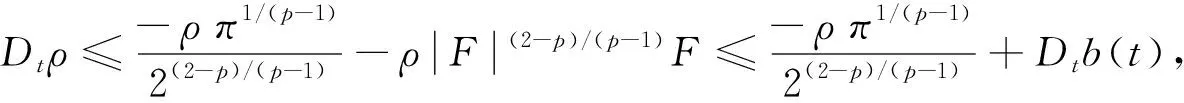




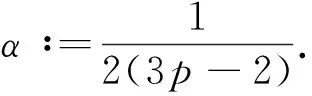

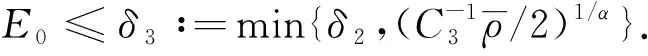
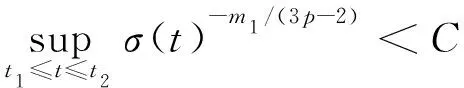

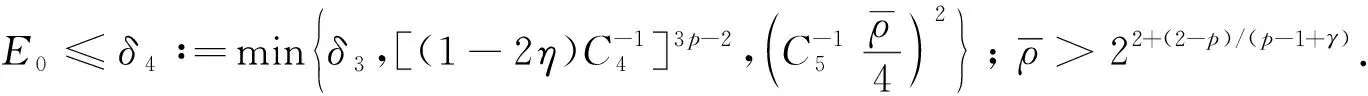

1.2 定理1的证明