基于频率的钢构件失稳监测研究
2020-08-28何法伟董永灿王寒冯颖合肥工业大学土木与水利工程学院安徽合肥230009
何法伟 ,董永灿 ,王寒 ,冯颖 (合肥工业大学土木与水利工程学院,安徽 合肥 230009)
0 前言
钢材具有优良的材料特性,是目前工程建设领域的主要材料之一。钢构件在使用过程中的失稳将导致重大事故,因此对其进行失稳监测具有重大意义。钢构件在失稳过程中,它的特征参数(如一阶固有频率)会发生显著的变化[2],当这种变化到达一定程度时,钢构件就会失去原来的稳定状态即失稳。分析钢构件失稳前频率的变化特征,能为其失稳监测提供依据。
1 轴心受压杆件的振动频率
压杆的稳定性分析存在多种方法,本文从结构动力学的角度对于理想的轴心压杆进行动力学分析,以两端铰支压杆为例,推导出两端铰支情况下的压杆各阶自振频率表达式,再引入材料力学中长度系数μ[1],用相当长度μl来表示不同杆端约束下的杆长,从而将铰支情况下的压杆各阶频率表达式[3]推广到其他约束情形下的压杆各阶频率表达式。

图1 压杆动力分析模型

分离变量可以得到:
由此得到两个独立的方程:

从上式可以看出,轴向力作用下的体系仍在做简谐振动。
引入参数α和g得:

则(3)式中第二式可写为:

为了求解式(5)令其振型 φ(x)=Derx,所以式(5)简化为:

求解得到4个根为:
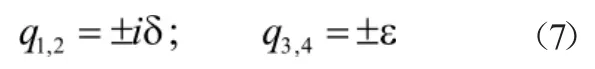
中间引入的参数δ和ε为:

将 φ(x)=Derx代入,得:

对于两端简支的压杆,其边界处的挠度和弯矩均为零,根据此边界条件可得:
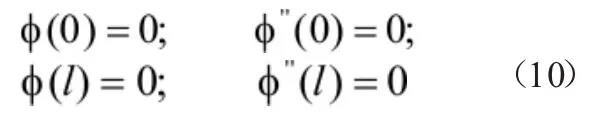
所以得到频率方程为:

简支压杆n阶自振频率:
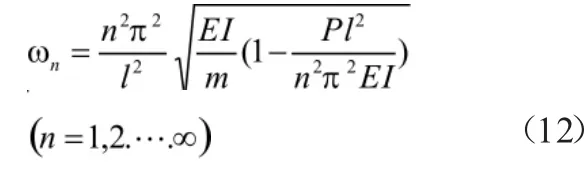
而对于不同的杆端约束情况,引入上文提到的长度系μ,则任意杆端约束下的压杆各阶频率表达式:
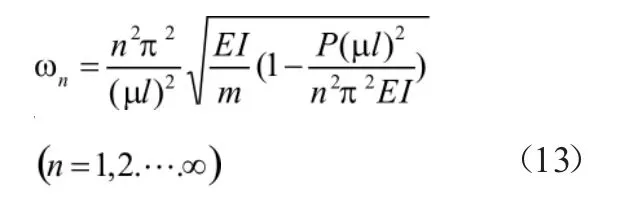
对于压杆的一阶固有频率而言,式(13)可简化为:

以两端铰支压杆为例(μ=1),做出ω-P间关系如图2所示。

图2 两端铰支压杆ω-P理论关系
由图2可知,随着杆端轴向压力不断增大,杆件的一阶固有频率不断减低,当轴向压力增至附近P=Pcr时,一阶固有频率降至0,此时认为压杆处于失稳状态,这为基于频率进行钢构件失稳监测提供理论依据。
2 有限元分析
利用Ansys软件建模,采用BEAM3单元网格划分为50格单元,进行预应力下的模态分析,提取结构的一阶频率,有限元模型如图3所示。

图3 有限元建模模型

图4 四种不同杆端约束下的压杆模型
用Ansys分别模拟两端铰支、一端固结一端无约束、一端固定另一端铰支,两端固定这四种杆端约束条件下的压杆模型,如图4所示。
由后续的分析可知4种杆件在轴向力的作用下,它们频率的变化特征是存在共性的,故首先对两端铰支压杆进行数值模拟。
在Ansys中建立如图3所示模型,并施加如图4所示的约束和荷载,构件L=1m,H=0.05m,B=0.03m,ρ=7800kg/m3,泊松比为 0.03,材料弹性模量E=2.06e11,采用BEAM3单元,网格划分为50份,模态提取一阶频率,加载结果如下表所示。

图5 两端铰支杆件加载示意图
两端铰支杆件在轴向力作用下一阶频率的变化
从表1中的数据可以看出两端铰支杆件在轴向力作用下,随着轴向压力的增大,一阶固有频率会降低。在低荷载处,压杆的一阶固有频率随荷载的增加降低较为缓慢,但在高荷载处压杆的一阶固有频率会随着荷载的增加急剧地下降[4],如图6所示。由欧拉临界公式可以算的该压杆失稳的临界压力为228728N,从表1中也可看出,当轴向压力趋向其欧拉极限时,一阶固有频率趋向于0,即压杆由稳定状态趋向失稳状态。
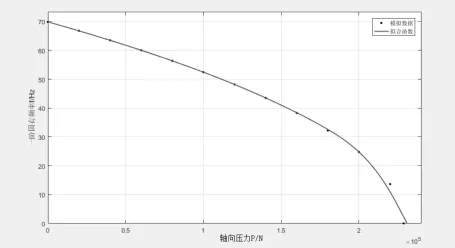
图6 两端铰支压杆ω-P的关系
将压杆的轴向压力同一阶固有频率的二次方进行函数拟合,如图7所示。

图7 两端铰支压杆ω2-P的关系

图8 其余三种压杆ω-P和ω2-P的关系
由图7中拟合函数可知,两端铰支杆件在轴力作用下,结构的轴向压力同一阶固有频率呈二次方线性关系,且数值模拟出的数据点同拟合的一次函数有相当高的重合度。
其余3种约束情况亦进行同两端铰支压杆相同的模拟分析步骤,将3种状况下模拟得来的数据绘制在同一幅图中,如图8所示。
为了分析的方便,每种约束情况的压杆的截面形状以及弹性模量等数据均相同,唯一的改变量就是压杆的长度,即每种约束的压杆μl相同且都等于1m,这样它们的欧拉极限就都在228728N附近。
数据1为一端固结另一端无约束压杆,L=0.5m;数据2为一端固定另一端铰支压杆,L=1.5m;数据3为两端固定压杆,L=2m。
根据图8可以分析出其他几种杆端约束下压杆的一阶固有频率变化特征同两端铰接压杆一阶固有频率的变化特征相同,轴向压力同一阶固有频率呈二次方线性关系,当轴向压力趋近欧拉极限时,压杆一阶固有频率趋于零,压杆失稳。
3 基于频率的失稳监测
本文采用加速度计(拾振器)来实现受压钢构件的频率测定,将加速度传感器安装在钢构件上,测定结构物在振动时的加速度,通过对加速度积分求位移,利用振幅的衰减关系求解结构的固有频率等动力特性参数。加速度计的特点是重量轻、体积小,因此测量值受振动自身影响较小,可以较为方便的布设在轴心受压构件上,能够满足单一受压钢构件的测量要求。
在测量时,加速度计需要和测定点直接接触,同时需要采用专用配线连接加速度计和中央记录单元,需要相关的信号放大处理及降噪处理等措施来保证测量精度。将记录的测量信息由动态信号分析仪处理输出频率等振动参数,配合微型处理器(如单片机)等对钢构件失稳情况进行判断,若发生失稳则发出警告,则可以达到失稳监测的目的。由于在高荷载处压杆的一阶固有频率会随着荷载的增加急剧的下降,为避免受压构件失稳丧失承载力对结构整体失稳造成影响,需要当ω≤ω'(ω'≥0)时就进行预警,ω'的设定需要结合材料的特性进行进一步的研究。
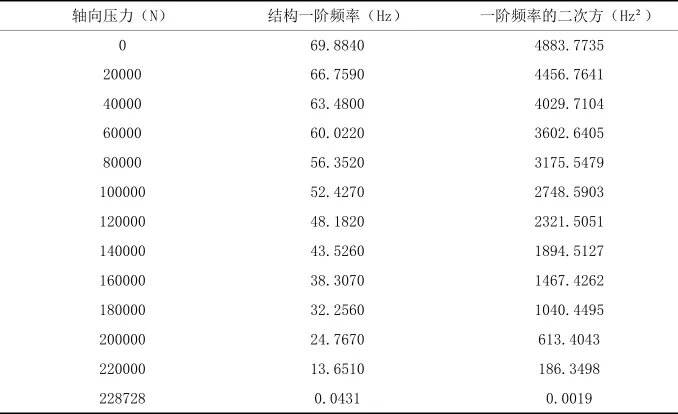
两端铰支杆件在轴向力作用下一阶频率的变化
基于频率的失稳监测流程如图9所示。
4 结语
失稳监测对钢结构的安全具有重大意义,钢结构在失稳过程中所表现的轴向压力同频率的特征关系对钢结构的监测具有非常重要的理论指导作用。从上述的分析中可以得出如下几个结论:
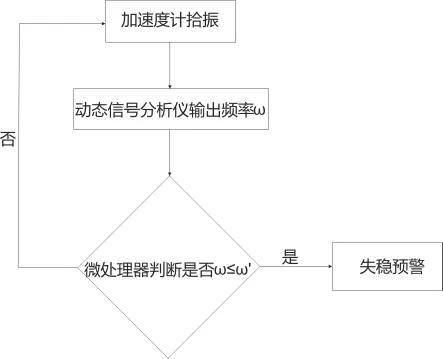
图9 基于频率监测流程图
①钢结构的一阶固有频率同轴向压力有关,随着压力的增大而减小,当结构发生曲屈失稳时,一阶固有频率降低到0;
②一阶固有频率在低荷载区降低较为缓慢,而在高荷载区下降迅速,即在临界失稳的状态,结构的一阶固有频率会急剧地降低至0;
③不论何种杆端约束形式的压杆,其轴向压力同一阶固有频率呈二次方成线性关系。
