基于第一性原理计算的镍基单晶高温合金掺杂的机器学习研究
2020-05-29吴雨沁
肖 斌 吴雨沁 刘 轶
(1.上海大学理学院物理系,上海 200444; 2.上海大学材料基因组工程研究院,上海 200444;3.上海大学钱伟长学院,上海 200444)
高通量实验、高通量计算和材料数据分析是材料基因组工程研发方法的三大要素[1- 2]。机器学习是针对材料数据进行挖掘分析、描述复杂材料构效关系的重要手段。材料的数据来源有实验[3]、计算[4]或数据库。基于密度泛函理论(density functional theory, DFT)的第一性原理计算有助于深入理解微观机制、发现新材料,但由于昂贵的计算成本限制了其在时间和空间上及考察的构型种类和数量上的应用。第一性原理计算可以通过高通量的方式系统地研究大量的材料体系和构型,由此产生的计算数据可进一步与机器学习建模结合,使得更为高效的材料性质预测成为可能。因此将高通量计算和机器学习方法相结合能够加速材料的计算研究。
Curtarolo等[5]、Meredig等[6]、Carrete等[7]、Faber等[8- 9]、Seko等[10]、Deml等[11]和Ward等[12]使用成分信息构建数据集,对不同的物理性质进行预测,其优点是简单灵活且适用面广。但需要大量的DFT计算数据才能构建较为准确的机器学习模型,且材料经常有同素异构现象,即相同成分有多种晶型的“简并”,其性质也可能有所差别。因而仅依据成分信息构造描述因子进行机器学习预测具有很大局限性。Togo等[13]、Kong等[14]、Jong等[15]和Ward等[16]开始引入全局结构信息进行建模,预测目标也是全局的材料性质,如材料的形成能或内聚能。但目前能够针对局部晶体结构的描述因子和材料局部性能的机器学习预测研究还较少见。
为了预测材料的局部性质,需要能够描述晶体局部成分和结构特征的描述因子。本文以晶体掺杂元素位点置换为例,提出了“成分- 结构”描述因子模型(composition- structure model, CS model),可同时考虑晶体结构的局部成分和结构特征。CE模型将掺杂元素作为中心参考位点,以其第一、二近邻原子作为环境,构建基于二维成分- 结构描述因子矢量的机器学习模型,描述合金元素掺杂引起的体系局部能量和结构变化。通过将元素的基础性质投影到“成分- 结构”模型上构建描述因子,并分别使用支持向量回归(support vector regression, SVR)方法和随机森林(random forest, RF)方法进行机器学习训练建模和预测。重点是在“已知”合金元素掺杂数据的基础上训练构建机器学习模型,预测“未知”新元素掺杂引起的局部结构和能量变化。
1 计算方法
1.1 掺杂元素占位的第一性原理计算
本文使用第一性原理VASP[17]软件对镍基单晶高温合金掺杂元素的置换占位构型进行系统的DFT计算。以稳定状态下的晶格常数分别建立了γ相和γ′相的2×2×2超胞模型。考虑各体系中置换元素的第一、二近邻,分别在γ相和γ′相中建立了2种和4种不等效置换位点对。考虑了镍基单晶高温合金中常见的11种合金化元素M(Al, Co, Cr, Hf, Mo, Ni, Re, Ru, Ta, Ti, W)。这些合金化元素在6种不等效位点对上共构成451种置换构型体系。在2×2×2超胞模型计算中,体系的晶格常数固定,离子位置进行充分弛豫,电子再进行自洽计算得到体系总能量。DFT计算中采用广义梯度近似GGA- PBE泛函和PAW赝势,截断能为400 eV,能量收敛精度为10-5eV;离子弛豫时K点间隔为0.047 Å-1,电子自洽计算时K点间隔为0.028 Å-1。
几何优化计算获得各置换构型体系总能量后,通过式(1)、式(2)分别计算了双位点置换体系模型的单位点置换能(single- site substitution energy,ESS)和单个置换位点体系弛豫前后第一近邻局部平均键长变化量(change of local mean bond length, <Δd>)。
ESS= (Eα+M+EMO)- (Eα+MO+EM)
(1)
<Δd>=1/12∑ ( |ri′-ro′ |- |ri-ro| )
(i=1,2,…,12)
(2)
式(1)中:MO、M分别为置换位点置换前、后的元素;α为体系去除置换位点处原子的部分,α+M为置换后体系,α+MO为置换前体系;EMO、EM分别为置换前、后元素的体相单原子能量;ESS为单位点置换能,Eα+M为置换后体系的总能,Eα+MO为置换前体系的总能。式(2)中,<Δd>为体系弛豫前后单个置换位点第一近邻的局部平均键长变化量;参考置换位点的第一近邻共有12个原子,ro为体系弛豫前参考位点的坐标,ri为体系弛豫前参考位点的第一近邻原子中第i个原子的坐标;ro′为体系弛豫后参考位点的坐标,ri为体系弛豫后参考位点的第一近邻原子中第i个原子的坐标。
1.2 机器学习描述因子模型构建
通过将元素基础性质投影至局部几何结构构建描述因子,元素的基础性质见表1[18]。基于置换元素的主体与环境的局部相互作用这一物理思想,设计了“成分- 结构”模型,将体系的局部成分与结构信息纳入特征构建。同时为了与仅使用成分构建机器学习模型相比较,考虑置换位点及其第一、二近邻原子构成的局部团簇的元素成分,构建了成分描述因子模型。

表1 用于构建机器学习描述因子的元素和单质体相的基础性质Table 1 Elementary properties of elements and simple substance for constructing machine learning descriptors
本文采用Python中的scikit- learn模块[19]进行机器学习。使用random forest (RF)和suport vector regression (SVR)算法进行机器学习建模。分别使用11种元素体系中的含其中10种元素的数据集作为训练集,分别对含第11种元素的数据进行独立预测。训练机器学习模型时采取5折交叉验证,使用网格搜索方法优化超参数。以决定系数(R2)和平均绝对误差(MAE)作为机器学习模型性能的评分指标。因每次划分数据均为随机过程,为了数据分析的统计意义,每个阶段的机器学习均进行了20次取样,并对20次取样结果进行平均,即得到平均
2 结果与讨论
本文根据成分- 结构(CS)和成分(C)描述因子进行机器学习建模,使用random forest (RF)和suport vector regression (SVR)算法分别预测了11种掺杂合金元素在γ相和γ′相中的单位点置换能(ESS)和局部平均键长变化(<Δd>),最后根据R2与MAE讨论比较各机器学习模型的预测精度。
2.1 单位点置换能(ESS)
对所研究的11种合金化元素的单位点置换能分别进行机器学习预测,预测结果的R2和MAE统计如图1所示。根据CS模型构建描述因子,使用SVR和RF对γ相训练集进行预测的R2分别在0.96(CS- SVR)和0.98(CS- RF)以上,γ′相训练集的R2分别在0.91和0.96以上;使用C模型构建描述因子,使用SVR和RF对γ相训练集进行预测的R2分别在0.94(C- SVR)和0.97(C- RF)以上,γ′相训练集的R2分别在0.84和0.93以上。使用CS- SVR和CS- RF机器学习模型对γ相训练集进行预测的MAE分别在42和44 meV以下,γ′相训练集的MAE分别在82和79 meV以下;使用C- SVR和C- RF机器学习模型对γ相训练集进行预测的MAE分别在64和68 meV以下,γ′相训练集的MAE分别在185和137 meV以下。由此可见,无论是γ相还是γ′相,根据“成分- 结构”CS模型构建的描述因子比成分C模型具有更高的机器学习预测精度。在使用CS描述因子的机器学习中,SVR和RF方法的预测精度接近,说明CS描述因子对机器学习算法的选择不敏感。但在使用C描述因子的机器学习中,SVR和RF方法的预测精度差异较大,如C- RF比C- SVR对γ′相数据集的预测精度要高。总的来说,对γ相数据集的预测精度比γ′相要高,这可能与γ′相中的占位构型数量更多、复杂度更高有关。
对独立测试集的预测结果进行分析:使用CS- SVR方法预测时,γ相中Ru、W、Ta、Re和Cr等元素的R2分别达到0.96、0.88、0.87、0.85和0.83,置换能MAE分别为102.5、159.9、192.8、212.3和179.9 meV,而Al、Co、Hf、Mo、Ni和Ti等元素的R2均在0.80以下,且MAE更大;γ′相中Re、Hf和Ta等元素的R2分别为0.82、0.79和0.75,置换能MAE分别为219.1、227.6和194.1 meV,而其他8种元素的R2均在0.60以下,Al元素具有最小的R2(-4.65)和最大的MAE(1 560.6 meV)。使用CS- RF方法预测时,γ相中W、Cr、Re和Ni等元素的R2分别达到0.86、0.86、0.85和0.84,MAE分别为169.2、173.1、185.4和178.0 meV,其他7种元素的R2均在0.80以下,Ti元素的R2仅为-0.46,MAE为675.2 meV;γ′相中Co、W、Ta和Re等元素的R2分别达到0.89、0.80、0.79和0.76,MAE分别为174.0、211.1、207.5和243.1 meV,其他7种元素的R2均在0.75以下,Ti元素的R2为-0.46,MAE为569.9 meV。
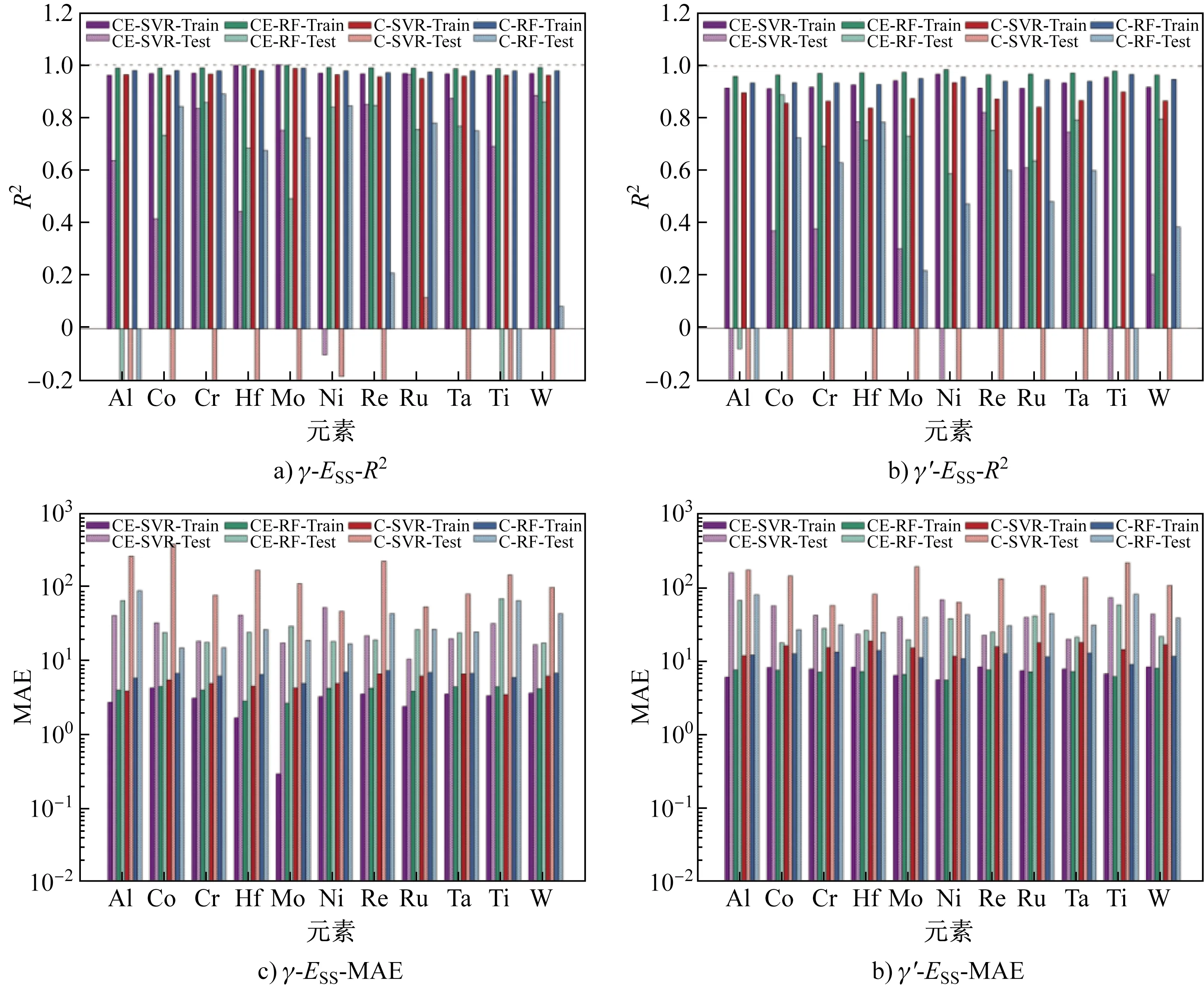
图1 单位点置换能机器学习预测结果(a,b分别为对γ相和γ′相中11种元素进行预测的R2,其中R2值小于-0.2时截断;c,d分别为对γ相和γ′相中11种元素进行预测的MAE)Fig.1 Prediction of machine learning for the ESS(a and b are the R2 of γ and γ′ phase for the eleven alloying elements, respectively, the R2 is truncated to -0.2 if it is smaller than -0.2; c and d are the MAE of γ and γ′ phase for the eleven alloying elements, respectively)
根据C描述因子构建机器学习模型,使用C- SVR方法预测时,γ相中所有元素的预测结果精度均比CS描述因子的低,Ru元素的R2最大仅为0.12,Ni元素的MAE最小,为453.0 meV;γ′相中所有元素的R2均为负值,Cr元素的MAE最小,达到560.4 meV。使用C- RF方法预测时,γ相中Cr、Ni和Co等元素的R2分别为0.89、0.84和0.84,置换能MAE分别为145.1、164.0和145.1 meV,其他8种元素的R2均在0.80以下,Al元素R2仅为-1.10,MAE达到864.2 meV;γ′相中Hf和Co等元素的R2分别达到0.78和0.73,MAE分别为240.9和262.2 meV,其他9种元素的R2均在0.65以下,Ti元素仅为-0.80,MAE达到794.4 meV。
使用RF方法对W元素的ESS进行预测,结果如图2所示。对W元素在γ相和γ′相的预测,使用CE模型进行数据挖掘时,其训练集和测试集的R2差值比使用C模型构建数据集时要小,表明使用CE模型构建数据集进行预测具有更小的过拟合度。同时,CE模型测试集的MAE相比C模型的更低 (γ相:169.2 meV vs 422.0 meV,γ′相: 211.1 meV vs 377.9 meV)。γ相的预测精度要高于γ′相,这可能是因为γ′相数据的复杂度高于γ相。

图2 使用RF方法对W元素的ESS进行机器学习预测与DFT结果的比较(a,c分别为γ相和γ′相中使用CS描述因子构建机器学习模型的预测结果;b,d分别为γ相和γ′相中使用C描述因子构建机器学习模型的预测结果)Fig.2 Comparison of the ESS of W- containing system obtained by machine learning and DFT (a and c are the results of γ and γ′ phase whose datasets constructed by the CS model, respectively; b and d are the results of γ and γ′ phase whose datasets constructed by the C model, respectively)
2.2 局部平均键长变化(<Δd>)
对局部平均键长变化<Δd>预测结果的R2和MAE统计如图3所示。使用CS- SVR和CS- RF对γ相训练集预测的R2均在0.99以上,γ′相训练集的R2分别在0.97和0.98以上;使用C- SVR和C- RF对γ相训练集预测的R2均在0.99以上,γ′相训练集的R2分别在0.94和0.98以上。使用CS- SVR和CS- RF对γ相训练集预测的MAE分别在0.8×10-3和1.0×10-3Å以下,γ′相训练集的MAE均在2.1×10-3Å以下;使用C- SVR和C- RF对γ相训练集预测的MAE分别在1.3×10-3和1.1×10-3Å以下,γ′相训练集的R2分别在4.2×10-3和2.1×10-3Å以下。

图3 局部平均键长变化<Δd>机器学习预测结果(a,b分别为对γ相和γ′相中11种元素进行预测的R2,其中R2值小于-0.2时截断;c,d分别为对γ相和γ′相中11种元素进行预测的MAE)Fig.3 Prediction of machine learning for the <Δd>(a and b are the R2 of γ and γ′ phases for the eleven alloying elements, respectively, the R2 is truncated to -0.2 if it is smaller than -0.2; c and d are the MAE of γ and γ′ phase for the eleven alloying elements, respectively)
对独立测试集的预测结果进行分析:使用CS- SVR机器学习模型预测时,γ相中Mo元素的R2达到0.90,MAE为4.3×10-3Å,而其他10种元素的R2均在0.77以下,且MAE更大;γ′相中Ta元素的R2为0.86,MAE为9.4×10-3Å,而其他10种元素的R2均在0.65以下,其中Co元素的R2最小(-11.89),MAE最大(80.6×10-3Å)。使用CS- RF机器学习模型预测时,γ相中Co、Mo和W等元素的R2分别达到0.97、0.95和0.94,MAE分别为2.4×10-3、2.5×10-3和2.8×10-3Å,其他8种元素的R2均在0.90以下,其中Ti元素的R2仅为-0.85,MAE为16.0×10-3Å;γ′相中W和Ni等元素的R2分别达到0.89和0.86,MAE分别为6.3×10-3和6.2×10-3Å,其他9种元素的R2均在0.84以下,Co元素的R2为-0.41,MAE为20.3×10-3Å。
使用C- SVR机器学习模型预测时,γ相中所有元素的预测结果精度较低,其中Mo元素的R2最大,为0.77,Cr元素的MAE最小,为15.6×10-3Å;γ′相中Mo元素的R2最大,为0.84,MAE最小,为8.8×10-3Å。使用C- RF机器学习模型预测时,γ相中Ti、Mo、W、Co和Ru等元素的R2分别为0.98、0.97、0.95、0.94和0.93,MAE分别为1.61×10-3、1.8×10-3、2.8×10-3、2.9×10-3和2.7×10-3Å,其他6种元素的R2均在0.90以下,Ta元素的R2为-0.36,MAE达到15.9×10-3Å;γ′相中Mo、W和Re等元素的R2分别达到0.97、0.92和0.91,MAE分别为3.7×10-3、5.5×10-3和6.2×10-3Å,其他8种元素的R2均在0.90以下,其中Hf元素的R2仅为-0.06,MAE达到26.4×10-3Å。
使用RF方法对W元素的<Δd>机器学习预测结果如图4所示。对W元素在γ相和γ′相中的预测,CS机器学习的训练集和测试集的R2差值比C机器学习的要小,表明使用CS描述因子构造机器学习模型比C描述因子的过拟合更小。同时,独立测试集的预测结果表明,CS机器学习模型预测的MAE相比C机器学习模型的更低(γ:2.8 vs 2.8×10-3Å,γ′: 6.3 vs 5.5×10-3Å)。
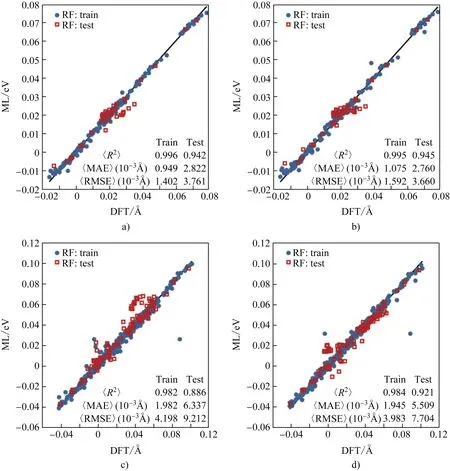
图4 使用RF方法对W元素的<Δd>进行机器学习预测和DFT结果比较(a,c分别为γ相和γ′相中使用CS机器学习模型的预测结果;b,d分别为γ相和γ′相中使用C机器学习模型的预测结果)Fig.4 Comparison of the <Δd> of W- containing system obtained by machine learning and DFT (a and c are the results of γ and γ′ phase whose datasets constructed by the CS model, respectively; b and d are the results of γ and γ′ phase whose datasets constructed by the C model, respectively)
2.3 合金元素置换能的机器学习预测
根据CS描述因子构建机器学习模型,使用RF对γ相和γ′相的置换能ESS的预测结果(CS- RF)MAE比CS- SVR方法的更小。使用CS- RF方法对γ相和γ′相的ESS的预测MAE结果统计如图5所示。

图5 使用CS- RF方法对γ相和γ′相中11种合金元素置换能预测的MAEFig.5 MAE of ESS for the eleven alloying elements in the γ and γ′ phases predicted by the CS- RF method
结果表明,使用随机森林(RF)方法对γ相和γ′相单位点置换能(ESS)进行CS机器学习建模时(CS- RF),W、Co、Mo、Re、Cr、Ta和Hf等元素的预测误差均小于300 meV, Ni和Ru元素的MAE在300~500 meV之间,Ti和Al元素的预测误差均大于500 meV。在11种合金元素中,使用CS- RF方法对Al元素的预测误差较大,且不同预测结果的误差变化大,而对W元素的预测误差相对较小且变化小。
综上所述,对不同掺杂元素的置换能的预测精度不一定相同,表明测试集中的预测元素与训练集中其他10种元素的平均性质的差异性不同:差异越小,预测误差也越小。置换能预测误差较大的合金元素是核外壳层p电子的Al和早期过渡族金属元素Ti,表明这些元素的性质与其他的中- 后期过渡族金属元素差异较大。预测误差较大时,不适合作为定量预测新元素性质的方法,该误差本身反映了预测元素与已知元素间性质的差异性或相似性。
3 结论
本文证明了通过将机器学习与第一性原理计算相结合能够加速对多元合金的新掺杂元素的局部能量和结构变化的有效预测。提出了适合描述晶体局部成分和结构的“中心- 环境”(CS)模型,将元素的基础性质投影到“中心- 结构”模型上构建描述因子,进而构建机器学习预测模型。对镍基单晶高温合金中常见的11种合金元素的单位点和双位点置换能及局部平均键长变化进行了预测。结果表明,使用成分- 结构信息描述因子构建的机器学习模型比传统的仅使用成分信息的机器学习模型具有更高的预测精度和鲁棒性。基于第一性原理的对新掺杂元素的能量和几何结构的机器学习预测有助于新型多元合金的成分设计。
