论整体序列音乐的接受困境——借助信息论“熵与冗余”的科学论证

沈 伟

1945年以降，整体序列主义从诸多音乐流派中脱颖而出，迅速席卷西方艺术音乐界，音乐创作霎时变为了学术研究。公众被漠视，作曲家则为其创作的合法性而理直气壮——“这种音乐充其量只不过是专门家的音乐，或由专门家写给专门家的音乐”。(1)〔美〕巴比特：《谁在乎你听不听？》，蔡良玉译，杨儒怀校，《中央音乐学院学报》，1998年第2期，第64页。倘若极赋音乐素养的听者能够从《月迷彼埃罗》中得到审美愉悦，恐怕他也会对《结构I》保持缄默。整体序列音乐的“语言”如此晦涩，以至于受过多年正统训练的专业音乐学习者都开始怀疑，其面对的这些文本是否由自己所熟知的“字母”组成。正如格林伯格所言：“前卫艺术对自身的不断专业化，它最好的艺术家乃是艺术家的艺术家，最好的诗人乃是诗人的诗人这一事实，已经疏远了不少以前能够欣赏雄心勃勃的文学艺术的人，现在他们已不愿，或无法获得一窥艺术奥秘的机会。”(2)〔美〕克莱门特·格林伯格：《艺术与文化》，沈语冰译，桂林：广西师范大学出版社，2015年，第9页。

不可否认，对于整体序列音乐这类在20世纪具有广泛影响力的先锋音乐，其在音乐接受方面存在的诸多问题，一直以来都令人们困惑不解。然而，整体序列音乐何以令人如此难以接受和理解？人们何以会对这种音乐产生巨大的疑惑甚至排斥？是否具有某些较为科学的方法或原理来解释这种令人困惑的音乐及现象？是本文所要尝试回答的问题。

一、熵与冗余——导致困惑的可能性

美国音乐学家伦纳德·迈尔(Leonard B.Mayer，1918—2007)于1967年出版的《音乐、艺术与观念——二十世纪文化中的模式与指向》是一部深入探讨20世纪音乐文化及其趋势动向的恢弘巨著。(3)〔美〕伦纳德·迈尔：《音乐、艺术与观念——二十世纪文化中的模式与指向》，刘丹霓译，上海：华东师范大学出版社，2014年。该书不乏许多富有理论价值、可付诸实践的创见，其中就包含本文接下来要详细讨论的两个重要概念——“熵”(entropy)与“冗余”(redundancy)。

“熵”与“冗余”这对概念均来自信息论。前者在现当代普通信息论基础教材中被定义为：“随机变量的平均不确定度的度量”；(4)〔美〕科弗、托马斯：《信息论基础》，阮吉寿、张华译，北京：机械工业出版社，2007年，第7页。后者表示：“多余的信息”。迈尔之所以要借用这两个看似和音乐毫不相干的概念，实则是要探究高度复杂的实验音乐的接受问题。以“冗余”为例，迈尔列举弦乐或木管独奏奏鸣曲的例证来做解释：“此类作品中，和弦并不以完整形式奏出，旋律‘线条’则以最精简的材料通过心智被建构出来。”(5)同注③，第16页。并且强调，冗余绝非贬义，它对于音乐各方面的学习与理解不可或缺：既能够帮助我们理解不完整的音乐事件，使聆听过程中短暂的思维停顿成为可能，又可以抵抗噪音。此外，他还将“冗余”分为感知冗余、风格冗余、以及作曲技术冗余等多种类型。最终，迈尔通过阐述论证得出结论——实验音乐由于包含极低的冗余而显得无比复杂且难以接受。(6)迈尔所言“实验音乐”(experimental music)泛指整体序列音乐、偶然音乐以及电子音乐等兴盛于20世纪50—60年代那些高度复杂且具有实验性的音乐。

然而，迈尔在《音乐、艺术与文化》中却并未对这两个概念进行刨根问底式的探究或对其理论观点进行实例分析式的论证。虽然以上两点丝毫不会影响迈尔对该研究领域做出的突出贡献，但因其所涉及的概念实属科学范畴，倘若不进行严谨的概念梳理与实际的分析论证，恐怕将难以增添其理论观点的信服度。因此，本文首先将从这两点出发，对“熵与冗余”这一对概念进行必要的解释，并在前人的研究基础上做进一步探究，最终是要论证迈尔理论观点的科学性与有效性。

(一)信息论中的两个概念——熵与冗余

“熵”这一概念最初源自物理学(热力学)。一般认为，熵的概念于1865年由德国物理学家克劳修斯(R.Clausius，1822—1888)提出，并用此来度量热力学过程的不可逆程度。1877年，奥地利物理学家玻尔兹曼(L.E.Boltzmann，1844—1906)说明了熵的微观意义，把熵作为物质系统内部无序程度的量度。然而，这一概念在信息论中的界定远非如此明晰。

20世纪中叶，美国科学家、信息论创始人克劳德·香农(Claude E.Shannon，1916—2001)将“熵”这一概念引入到信息论中。他在《通信的数学理论》(AMathematicalTheoryofCommunication，1948)中写道：“H(熵，译者注)……作为信息、选择和不确定性的度量，在信息论中起着核心作用。”(7)Claude E.Shannon，“A Mathematical Theory of Communication”，reprinted with corrections from The Bell System Technical Journal，July，October，1948，p.11.可以看出，香农对“熵”的定义并不仅限定于单一范畴，而是涵盖了“信息(information)、选择(choice)和不确定性(uncertainty)”三方面因素。但悉心观察不难发现，在普遍观念中，“信息”与“不确定性”似乎是一对截然相反的概念。通常认为，当我们获得了某种“信息”，便是消除了某种“不确定性”，而香农却在此将二者等同于一物。此外，当时另一位信息论领域的重要科学家沃伦·韦弗(Warren Weaver，1894—1978)也持相同观点：“唯一符合人们因自然需求而为‘信息’设定的量，正是热力学中的‘熵’。”(8)Warren.Weaver，“Recent Contributions to The Mathematical Theory of Communication”，ETC：A Review of General Semantics，September，1949，p.7.然而，美国数学家、控制论创始人诺伯特·维纳(Norbert Wiener，1894—1964)却提出：“信息量是一个可以看作几率的量的对数的负数，它实质上就是负熵。”(9)〔美〕诺伯特·维纳：《控制论：或关于在动物和机器中控制和通讯的科学》，郝季仁译，北京：科学出版社，1985年，第65页。

“熵”在信息论中的定义之所以如此混杂，其原因在于香农对“信息”一词的界定：香农信息论中的“信息”，实质上是指“信源”(information source)发出的包含各种可能性的总信息量。而人们普遍却仅仅将总信息量中有意义的那一部分称为“信息”，更准确地说，称之为“消息”(message)。因此，“熵”在信息论中用以表示无序、无意义、不确定性的信息量，被称为“信熵”(无意义信息)；而那些有序、有意义、确定性的信息量则被称为“消息”(有意义信息)。但即便如此，维纳所言“信息是负熵”该作何解释？首先，需要强调，维纳所说的“信息”是指“有意义信息”(消息)；其次，前文已经阐明，“信熵”是对无序、无意义、不确定性的度量，它与“信息”(消息)成反比：确定性(信息)的增加，就意味着不确定性(信熵)的消除(二者数量相等，意义相反)。因此，可以说，“负熵”与“信息”成正比——“信息”增加的量等同于“信熵”失去的量——即“信息是负熵”。为便于理解，下面将举例进行说明(见例1、例2)。

例1.

信熵100%

信源总量100%

例2.

信熵50% 信息(负熵)50%

信源总量100%

如上所示，以一条由十二个半音构成的序列为“信源总量”，假定获取信息的目标为任意调上的一个清晰完整的终止式，那么在这个限定下，例1所呈现的无序程度或不确定性最大，其信熵函量为100%。而在例1序列的基础上重新调整音的顺序后(例2)，其后半部分显然呈现出C调D—T进行，那么这一部分作为有意义信息，其信息函量为50%。根据前面提到的定义(信息增加的量等同于信熵失去的量)，进而证实——信息即是负熵。

相对于含义复杂的“熵”，信息论中“冗余”这一概念则较易于理解。首先，需要大致了解一下信息论的信息传输原理——通信系统的传输过程：信源发送消息到发送端(transmitter)，发送端将消息编码成适合信道(channel)传输的信号(signal)发出，经过噪音源(noise source)干扰，最终由接收端(receiver)接收信号并译码为消息发送给信宿(destination)。具体参见图1(10)图片引自Claude E.Shannon，“A Mathematical Theory of Communication”，reprinted with corrections from The Bell System Technical Journal，July，October，1948，p.11.。

图1.

由于噪音对信道的干扰，初始的消息不可能被全然保留且毫无误差地传送到信宿(消息接收的对象)。但现实的情况是，即便消息是不完整的，接受对象往往也能够捕捉其意义。对此唯一的解释是——信息中存在不同程度的冗余。或者说，在一条消息中，通常同时存在“必不可少的信息”与“多余重复的信息”。对于那些多余的信息，韦弗认为：“称其为冗余是合理的……因为即便缺少了它，消息基本上仍是完整的，或者至少已经形成了。”(11)Warren.Weaver，“Recent Contributions to The Mathematical Theory of Communication”，ETC：A Review of General Semantics，September，1949，p.7.此外，香农指明：“如果信源已经有了一定的冗余，并且在与信道匹配时没有试图消除它，那么这种冗余将有助于对抗噪音。”(12)同注⑩，p.24。这也正是为什么一则消息或一个音乐片段，在缺失了一些字或音时，我们仍然可以领会其意义。

虽然前文已经解释了“熵”与“冗余”这一对概念在信息论中的意义，但诘问接踵而至——信息论在实际的音乐作品分析中是否具有可行性？以及如何证明迈尔理论观点的科学性与有效性？对于这类诘问，本文接下来将分别作答。

(二)信息论分析的具体实践

在信息论中，“熵”与“冗余”不仅是两个用以理解的概念，它们实质上是可以进行科学度量的函量。由于下文涉及具体音乐作品的“信息论分析”(information theory analyses)，故在此对“熵”与“冗余”的数学运算公式进行必要的介绍。首先，香农用概率统计的方法给出“熵”的定义：(13)关于“熵”数学公式的详细内容可参见Claude E.Shannon，“A Mathematical Theory of Communication”，reprinted with corrections from The Bell System Technical Journal，July，October，1948，p.11.

其中，H为“熵”(单位为：bit)；∑(sigma)为求和符号，表示从i开始，相加到n；p(probability)为概率；log(logarithm)为对数(底数为2)；由于p必须满足0≤P≤1，且log p为负数，所以∑前需加上负号(-)，H才能成为正值。

根据香农对“冗余”的定义：“一个信源的熵与它所能达到的最大值之比(且仍然被限制在相同的符号内)被称为‘相对熵’……一减去相对熵就是‘冗余’。”(14)Claude E.Shannon，“A Mathematical Theory of Communication”，reprinted with corrections from The Bell System Technical Journal，July，October，1948，p.14.因此，“冗余”的数学表达式为(Hm为最大熵，或称Hmax.，其方程式为Hm=logN)：

乔尔·科恩(Joel E.Cohen，1944—)于1962年在一篇题为《信息论与音乐》(InformationTheoryandMusic)(15)Joel E.Cohen，“Information Theory and Music”，Behavioral Science，7(April，1962)，pp.137-163.的论文中，阐述、评价与总结了自20世纪中叶信息论创立以降，借用信息论的方法对音乐进行分析研究(从数学、心理学、美学等多个角度)的诸多实践与假说。单从数学统计分析的方面来说，列哈伦·希勒(Lejaren Hiller，1924—1994)与卡尔弗特·比恩(Calvert Bean，1928—)在随后的一份研究中(发表于1966年)体现出重要的开创性意义——文章开篇直言：“到目前为止，几乎没有人具体地检验信息论的概念是否确实提供了某种对音乐结构重要细节的定量度量。在此，我们将演示该理论在传统音乐形式研究中的初步应用。”(16)Lejaren Hiller，Calvert Bean，“Information Theory Analyses of Four Sonata Expositions”，Journal of Music Theory，Vol.10，No.1，Spring，1966，pp.96-137，p.97.目前国际上与信息论相关的音乐文献偏少，鲜有就某一项专题而开展的深入系统的研究，较为新近(2010)且涉及具体音乐作品(韦伯恩)的有美国爱荷华大学研究生院的一篇学位论文，但该文主要是从信息熵的角度探讨“音乐时间与可预测性之间的关系”，参见：Sarah Elizabeth Culpepper，Musical Time and Information Theory Entropy，Graduate College of The University of Iowa，2010，p.2.虽然希勒与比恩的这篇文章成文于1966年，但其仍具有较高的学术及理论价值且与本文的研究课题密切相关，故本文对相关论题的探索将以该文为研究基础。这篇文章主要是对如下四首钢琴奏鸣曲的呈示部进行信息论分析：

1.莫扎特《C大调钢琴奏鸣曲》(Mozart，PianoSonatainCMajor，K.545，1788)

2.贝多芬《e小调钢琴奏鸣曲》(Beethoven，PianoSonataineMinor，Op.90，1814)

3.贝尔格《b小调钢琴奏鸣曲》(Berg，PianoSonatainbMinor，Op.1，1908；revised 1920)

4.亨德米特《G大调钢琴奏鸣曲》(Hindemith，PianoSonataNo.2inGMajor，1936)

首先，作者假定音乐信息测量的最大值为12——即平均律中的十二个半音(八度不改变其性质)。在此基础上又分为不包含等音的“12音”体系与包含等音的“21音”体系(不计以重升、重降记号标记的等音)，每首作品都同时使用以上两种划分体系，并且采用两种计数方法：1.计数方法A，仅计算音符的数量；2.计数方法B，以十六分音符为一个单位，根据音符时值的递增而递增(十六分音符=1；八分音符=2；附点八分音符=3；四分音符=4；以此类推)，计算与音符相对应的时值数量。其次，作者根据曲式结构将每首作品划分为五个部分，分别对应奏鸣曲呈示部的主题、连接、副题、发展、终止。最后，使用信息论各类方程式计算得出每部分相应结果，再相加取平均值。

研究结果表明，上述四首钢琴奏鸣曲呈示部的“冗余”分别为(采用“12音”体系；计数方法A)：Mozart 26.6%；Beethoven 16.2%；Berg 1.6%；Hindemith 6.3%。可以看出，越是偏离调性且形式内容越复杂的作品，其冗余越低。因此，这份重要的研究证明，采用信息论的方法测量音乐作品的冗余具有一定的可行性与有效性。

二、信息论分析的初步尝试

鉴于希勒与比恩的这份研究仅将研究对象限定在调性音乐范围内，并没有涉及无调性与序列音乐，故笔者尝试在前人的研究基础上使用实例分析的方式对“实验音乐由于包含极低的冗余而显得无比复杂且难以接受”这个论题做进一步论证。

笔者从浪漫派、无调性以及序列音乐三类风格中各挑选出一首作品，采用信息论的方法对三首作品的“冗余”进行了分析考察，其中无调性与序列音乐作为主要研究对象，浪漫派作品作为对比与参照。考虑到计算的复杂程度与信息论分析的完整性，本文所选曲目均为短小精炼的钢琴小曲，篇幅不超过22小节，演奏时长不超过1分钟。曲目如下：

1.舒曼《童年情景》(Schumann，ScenesfromChildhood，Op.15 No.1，1838)

2.勋伯格《六首钢琴小曲》(Schoenberg，6LittlePianoPieces，Op.19 No.5，1911)

3.施托克豪森《钢琴曲III》(Stockhausen，PianoPieceIII，1952)

(一)分析的方法与步骤

本文使用的信息论分析方法直接借鉴了希勒与比恩的研究。首先，假定音乐信息测量的最大值为12(八度不改变音的性质)，设N=12，则最大熵Hm=logN=log212=3.585bit(保留小数点后三位)；其次，采用不包含等音的“12音”体系，统一以音名加升记号(#)表示非基本音级，以实际音高为基准，记谱为非升号各音根据等音原则做调整(例如bD记为#C，bbF记为#D)；最后，分别采用上文所述两种不同的计数方法(A/B)对每首作品进行统计分析，再通过各类方程式计算得出结果(由于每首乐曲的篇幅都十分简短，故进行整体计算，不做段落划分)。具体分析步骤如下：

计数方法A

1.统计每首作品的音符数量：计入音符实际出现数量，不计音符时值与改变音符时值的各种演奏记号(例如断奏或延音记号)，使用延音线的音符无论延长多少均计1个单位；

2.统计十二个半音在每首作品中出现的概率(各音数量与音符总和之比)；

3.使用方程式运算得出每首作品的熵值；

4.使用方程式运算得出每首作品的冗余。

计数方法B

1.统计每首作品中与音符相对应的时值数量：以十六分音符为基本单位1，根据二等分原则递增或递减(例如八分音符=2，三十二分音符=0.5)，连音符与基本音符等同，不计改变音符时值的各种演奏记号(例如断奏记号、延音记号)，使用延音线的音符根据延长内容计入相应时值；

2.统计十二个半音在每首作品中出现的概率(各音时值数量与时值总和之比)；

3—4方法同A。

统计分析后的详细数据参见表1—3。

表1.舒曼《童年情景》

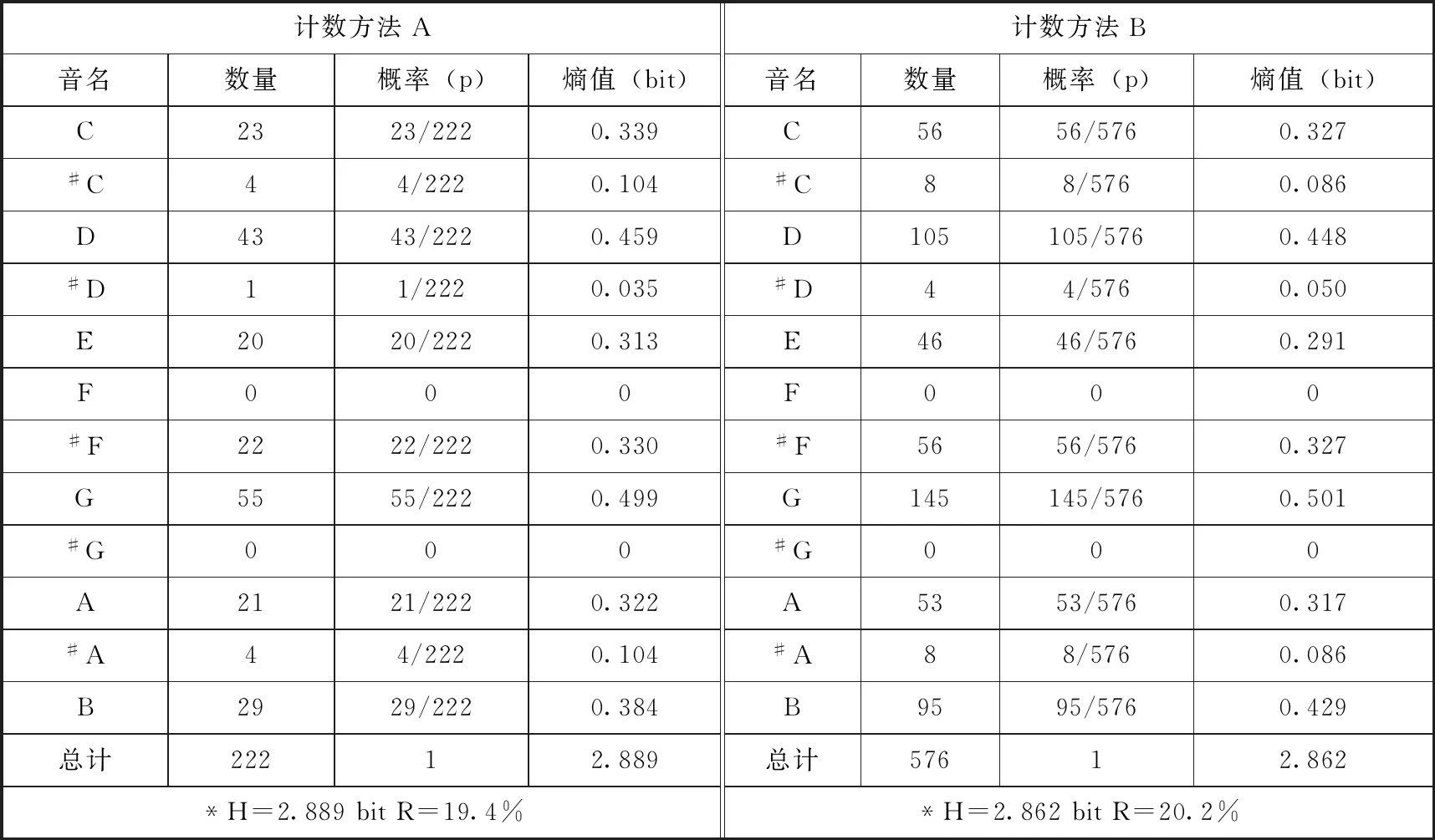
计数方法A计数方法B音名数量概率(p)熵值(bit)音名数量概率(p)熵值(bit)C2323/2220.339C5656/5760.327#C44/2220.104#C88/5760.086D4343/2220.459D105105/5760.448#D11/2220.035#D44/5760.050E2020/2220.313E4646/5760.291F000F000#F2222/2220.330#F5656/5760.327G5555/2220.499G145145/5760.501#G000#G000A2121/2220.322A5353/5760.317#A44/2220.104#A88/5760.086B2929/2220.384B9595/5760.429总计22212.889总计57612.862*H=2.889bitR=19.4%*H=2.862bitR=20.2%

表2.勋伯格《六首钢琴小曲》

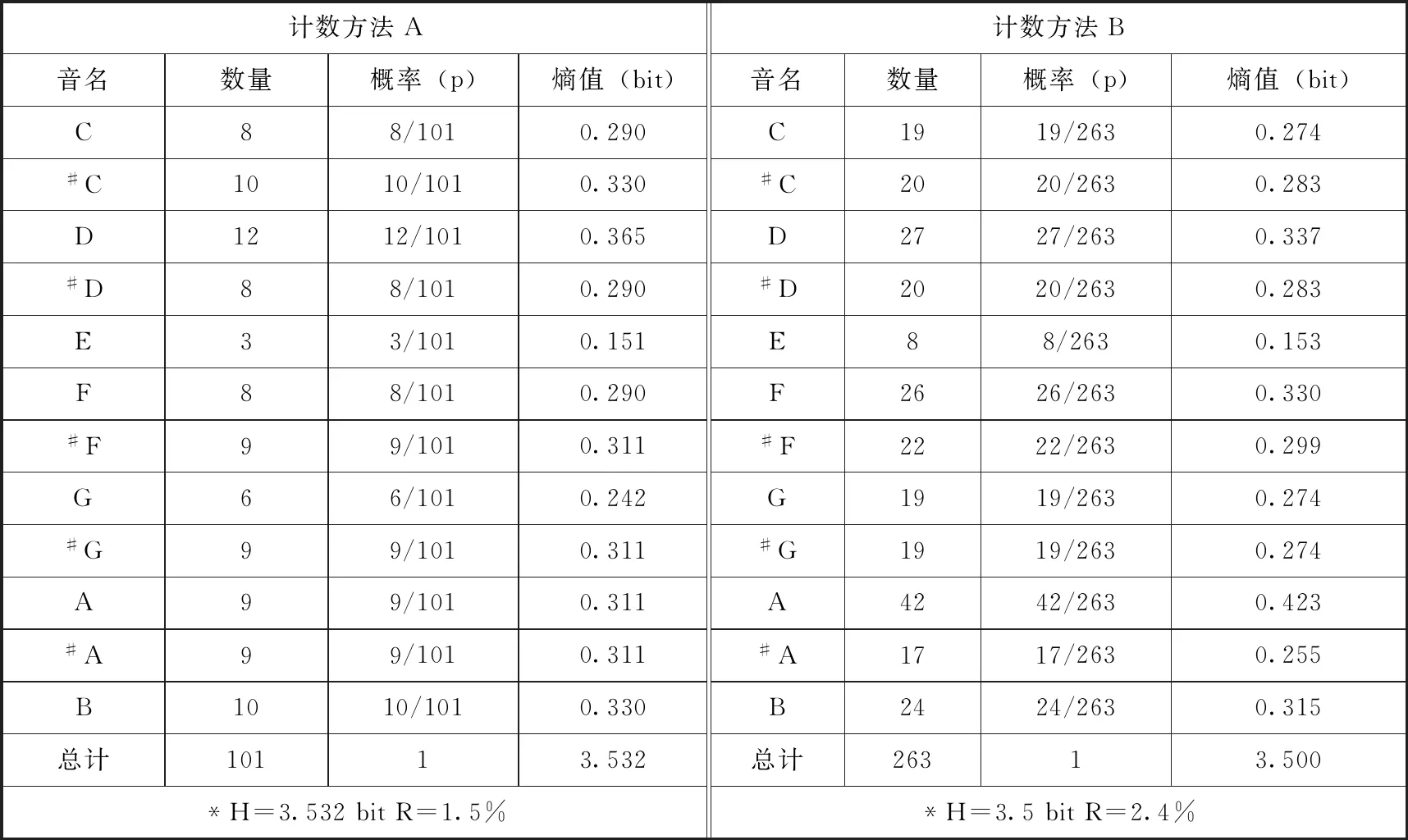
计数方法A计数方法B音名数量概率(p)熵值(bit)音名数量概率(p)熵值(bit)C88/1010.290C1919/2630.274#C1010/1010.330#C2020/2630.283D1212/1010.365D2727/2630.337#D88/1010.290#D2020/2630.283E33/1010.151E88/2630.153F88/1010.290F2626/2630.330#F99/1010.311#F2222/2630.299G66/1010.242G1919/2630.274#G99/1010.311#G1919/2630.274A99/1010.311A4242/2630.423#A99/1010.311#A1717/2630.255B1010/1010.330B2424/2630.315总计10113.532总计26313.500*H=3.532bitR=1.5%*H=3.5bitR=2.4%

表3.施托克豪森《钢琴曲III》

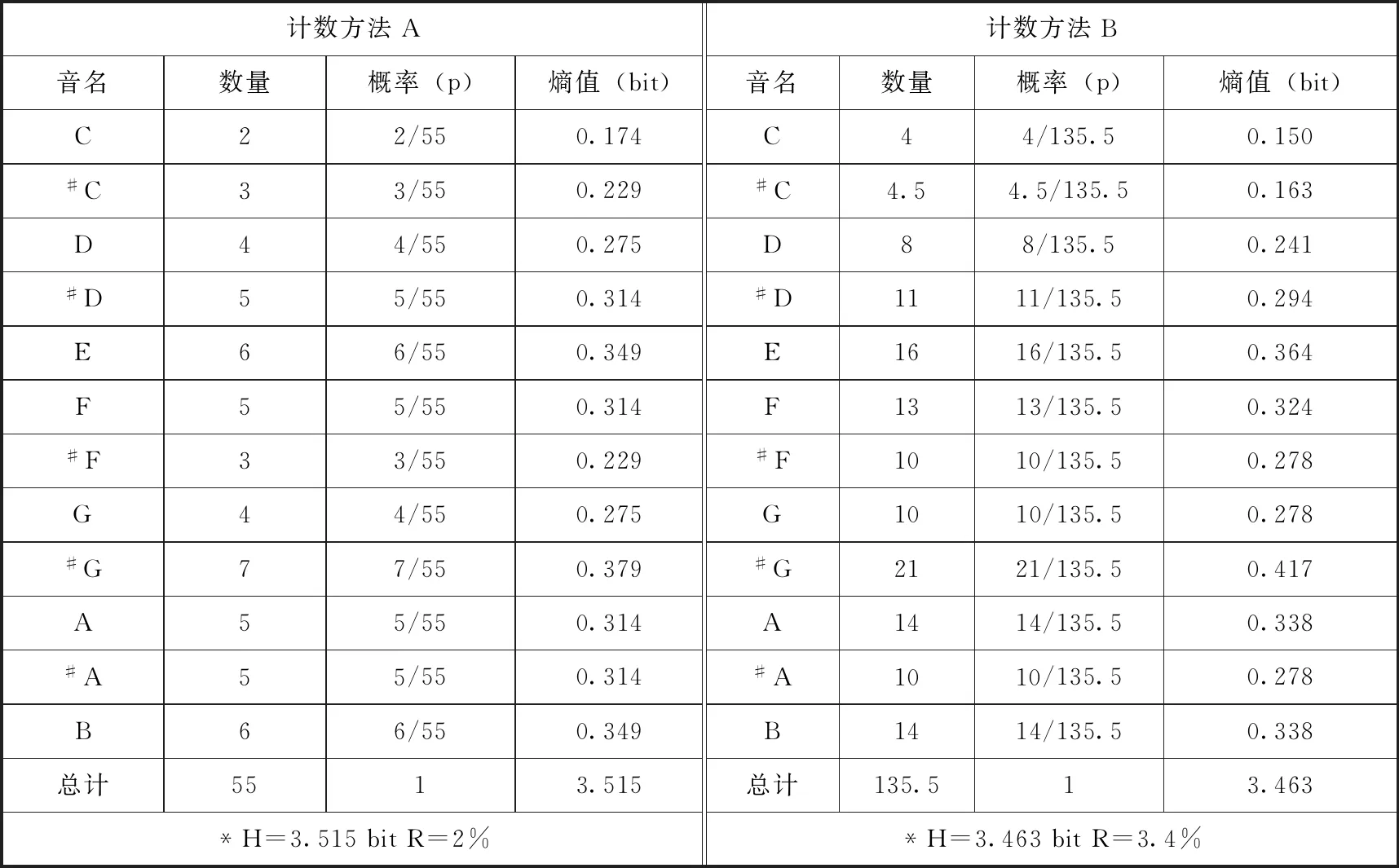
计数方法A计数方法B音名数量概率(p)熵值(bit)音名数量概率(p)熵值(bit)C22/550.174C44/135.50.150#C33/550.229#C4.54.5/135.50.163D44/550.275D88/135.50.241#D55/550.314#D1111/135.50.294E66/550.349E1616/135.50.364F55/550.314F1313/135.50.324#F33/550.229#F1010/135.50.278G44/550.275G1010/135.50.278#G77/550.379#G2121/135.50.417A55/550.314A1414/135.50.338#A55/550.314#A1010/135.50.278B66/550.349B1414/135.50.338总计5513.515总计135.513.463*H=3.515bitR=2%*H=3.463bitR=3.4%

关于信息论分析的具体计算过程，笔者将以施托克豪森《钢琴曲III》为例(采用计数方法A)进行演示：首先，将表3中所统计的与十二个半音相对应的概率p(2/55、3/55、3/55……6/55)的数据代入信息熵H的方程式进行运算：

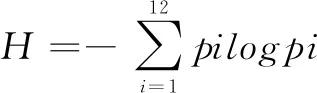
经过计算，得出该作品的熵值为3.515 bit，再将熵值代入冗余R方程式进行运算，最终得出施托克豪森《钢琴曲III》的冗余为2%：

(二)分析的结果

笔者通过两种计数方法的统计分析，最终得出三首作品的分析结果为(表4—5)：

表4.分析结果(计数方法A)

作曲家舒曼勋伯格施托克豪森熵值2.889bit3.532bit3.515bit冗余19.4%1.5%2%

表5.分析结果(计数方法B)

作曲家舒曼勋伯格施托克豪森熵值2.862bit3.5bit3.463bit冗余20.2%2.4%3.4%

这一结果表明：无论是勋伯格的无调性音乐，还是施托克豪森的序列音乐，二者的冗余程度均远远低于舒曼的作品(只有不足4%的冗余)，由此可以推断，导致无调性与序列音乐复杂且难以理解的原因(或可能性)之一，在于两者具备一个相同的特性——极低的冗余。(17)通过观察表1中的统计数据不难发现，舒曼的作品通篇未出现F和#G两音(及其等音#E、bA)，而G与D则分别出现55、43次(计数方法A)——毋庸置疑，G、D作为该作品(G大调)的两个支柱音受到了频繁使用。这一因素直接决定了一部音乐作品冗余的程度：由于“熵”在等概率中最大，因而当无调性与序列音乐尽可能“平均”运用十二个半音时，其熵值将远高于“不平均”对待十二个半音的调性音乐。然而，出乎意料的是，在听觉和形式上更加复杂多变的序列音乐(施托克豪森)，其冗余竟略高于勋伯格的无调性钢琴小品。不但如此，通过对比其他作品的分析结果可以看出，施托克豪森的这首序列音乐作品的冗余不仅高于无调性音乐，甚至高于极端半音化的有调性音乐。在希勒与比恩的研究中，冗余程度最低的作品是贝尔格钢琴奏鸣曲Op.1(仅1.6%冗余)，该曲虽然不是一首无调性或序列音乐作品，但因其极端半音化的音乐特征，使得作品的调性几近崩溃，十分接近无调性音乐风格。然而，这首乐曲传达出的丰富细腻的音乐性以及令人难忘的主题动机与其极低的冗余不甚相称，至少从听觉层面来说，勋伯格与贝尔格的这两部作品的可理解性要略高于施托克豪森。那么，到底是何种因素导致这一令人费解的现象？

三、信息论分析的结论

针对上述分析结果中的困惑——施托克豪森序列音乐作品的冗余高于勋伯格无调性与贝尔格半音化音乐作品，笔者认为，这首先与信息论分析的局限性以及音乐自身的特殊性相关。在前人的信息论分析与本文的初步尝试中，研究对象(音乐材料)的具体分析主要涉及“音高”层面，即便“计数方法B”在一定程度上对“时值”进行了统计分析(实际上并不具备可靠的有效性)，但在“音色”和“力度”方面，所有研究均未对此展开详细深入的考察。原因有二：1.目前尚无一套能够科学有效地对音乐材料的“时值”“力度”以及“音色”层面进行统计分析的信息论分析方法(纵使有这种方法，其可行性与有效性也应当受到质疑)；2.音乐自身存在特殊性。一部音乐作品是由音高、时值、力度、音色等诸多元素组合而成的综合体，它是作为一个完整的个体被感知。其中，核心元素是“音高”，其他元素必须与音高相结合才具有真实效用，任何脱离音高的统计分析都将以失败告终。因此，当研究的范畴仅涉及“音高”层面时，序列音乐的冗余比无调性音乐略高也就不足为奇了。然而，关键的问题在于，整体序列音乐是否——正如它从听觉上所体现的那样——较之以往任何音乐都更加难以理解，具有更低的冗余？笔者认为，答案是肯定的。虽然信息论分析存在一定的局限性，但其原理的真实有效性是无可撼动的，它对于问题的探索有着极为重要的指导意义。对此，笔者将结合信息论的某些原理与迈尔的某些观点对该论点进行阐述。

伦纳德·迈尔在《音乐、艺术与观念》的第三部分中，详细考察了高度复杂的实验音乐的理论与实践问题。关于整体序列音乐，作者指出：“通常，似乎音乐的预先组织和安排越彻底，它在感知上的模式化和组织性就越弱。”(18)〔美〕伦纳德·迈尔：《音乐、艺术与观念——二十世纪文化中的模式与指向》，刘丹霓译，上海：华东师范大学出版社，2014年，第291页。这一观点切实反映了人们对这类音乐的听觉感受。普遍来说，一部严格意义上的整体序列音乐至少预先设定了音高、时值以及力度的序列。但对于非序列音乐而言，一部音乐作品的音高、时值以及力度的安排与使用主要取决于音乐自身的发展逻辑和创作者的实际需要。当这些音乐元素被人为地控制限定后，音乐并非变得井然有序，而是成为一团杂乱无章、令人无法捉摸的“有声编码”。然而，何以产生如此这般后果？若要回答这一诘问，就需要借助信息论中的某些原理来解释。

根据信息论中“熵”的定律——熵是对无序、无意义、不确定性的度量，熵与信息(消息)成反比——可以得出：一部音乐作品的熵越大，其信息量就越少；信息量越少，其冗余就越低。进而可以推断，一部音乐作品中无序、无意义、不确定性的内容越多，其冗余就越低。前文已阐明，非序列音乐中的各个音乐元素(音高、时值、力度)是按照长期以来逐步发展成熟的音乐写作模式(即某种被人们称为写作“常规”或“惯例”的作曲模式)结合创作者的主观意识进行择选的，其中每项音乐元素都已经形成一套复杂精密的系统，所有元素都在创作者有意识的感知下操作运行，以有序的形态在确定性的方式下达到有意义的目的(19)此处所言“有意义”并非指某种现实“功用”或“价值”，而是指音乐元素的组织符合某种写作惯例。——即建构一部符合特定作曲模式的独立完整的音乐作品。实际上，这些音乐元素本身是一个为符合不同时期人们对音乐的审美感知而不断转向“有序”的发展过程。虽然这一过程在20世纪逐渐瓦解，但不可否认，即使是无调性音乐，其中仍然具有许多“有序”的成分，因为作曲家此时并没有完全控制音乐中任何一项元素。即便极端半音化的音乐和无调性音乐在“音高”层面有着不同程度的无序与不确定性，但作曲家仍然可以借助时值与力度的变化使音乐获得张力，从而体现出某种音乐上的“情绪”。这解释了为何贝尔格的钢琴奏鸣曲只有1.6%的冗余，但其仍具有丰富的音乐性。相比较而言，整体序列音乐虽然事先预设了各个音乐元素的序列，但音乐在发展过程中却是随机、不确定且无法预测的(对于“共性写作时期”某些技巧娴熟的作曲家而言，一部音乐作品在未写出之前其部分或完整形象可能就已经被预见)，原因在于预设序列的方法消除了人的参与——即创作者不再对音乐元素进行符合创作主体或他人审美感知的艺术化处理。因此，整体序列音乐中的音乐元素呈现出的是一种“无序”状态——即其音高、时值、力度等各个音乐元素的熵值极高、冗余极低。这使得此类音乐产生不了传统调性音乐甚至无调性音乐的那种音乐结果(或效果)，几乎无法唤起听者的感知认同，即便音乐中出现某些令人们感到“似曾相识”的片段，这也并非作曲家有意为之——其仅仅是作品中各音乐元素的“偶然结合”。

另一方面，伦纳德·迈尔从感知心理学的角度解释了上述问题。迈尔指出：“由于音高是现象性的，在给定一个相对稳定的时间模式时，便有可能将一个音高序列的移位、倒影或逆行感知为与原型类似……但时值模式却不能……尽管其他声音要素(力度、音色、触键等等)的序列化包含着一种理论上的排序，这种排序同样不会诉诸感知。”(20)〔美〕伦纳德·迈尔：《音乐、艺术与观念——二十世纪文化中的模式与指向》，刘丹霓译，上海：华东师范大学出版社，2014年，第291页。笔者认为，产生这种现象的原因在于：1.各音乐元素之间具有不同的特性，其中音高的特性最为显著、最能刺激人的感知，而其他音乐元素的刺激性较弱且需要诉诸音高才能发挥效用；2.听者通常不会孤立地关注音乐中的个别元素，而是将音乐作为一个整体去聆听。此外，迈尔认为：“我们对特定的经验和事物加以理解和记忆，是将之看作来自或偏离某些范式，这些范式是我们容易且高效地对大量信息进行‘编码’和记忆的方法。缺少了这些范式，记忆和感知将永远陷于充满孤立细节的不可理解的混乱中。”(21)同注，第294页。迈尔所言“范式”，是指音乐中的旋律模式、节奏组合、和弦进行、模仿对位、曲式结构等一系列独特且具有典范意义的形式，这些范式正是笔者在前面提到的“长期以来逐步发展成熟的音乐写作模式”中的各个组成部分。因此，一旦音乐中的各元素被毫无关联地组织起来(需要强调，音乐元素的组织与逻辑性相关，并不受独立性影响)，那这将超出听者的“信道容量”(channel capacity)——即超出听者的感知范畴。对此有一个清晰的例证：当我们同时聆听两首无论体裁、风格都不尽相同的乐曲时(即便是听者非常熟悉)，往往表现为或仅能专注于其中一首(有可能两首相互转移注意力)；或面对一团“陌生的”音响浑然不知所措。然而，无论一首赋格曲的声部多么繁复，我们在聆听时却不会觉得混乱无章。原因正如前文所言，当音乐材料(或元素)并非由创作者有意识地按照某种音乐逻辑进行组织时，其产生的音乐结果将不被人们所感知。

至此，本文通过借鉴伦纳德·迈尔及其他研究者的理论观点和成果、吸收了信息论中的某些原理并采用信息论的方法进行了实例分析与对比论证后，最终认为：整体序列音乐因其音高、时值、力度等各个音乐元素极低的冗余程度，导致其形式结构极端无序而复杂，超出一般性的音乐感知范畴，难以被听者理解与接受。

(附言：本文的指导教师是班丽霞教授，特此感谢！)