“五例”教学法引领几何核心概念深度理解

吴火桂

摘要：在几何核心概念的教学中，教师可尝试运用易良斌老师提出的“五例”教学法，即范例、正例、特例、反例、错例，以促进学生对几何问题的深度理解。

关键词：几何核心概念;“五例”教学法;深度理解

初中学生开始几何内容的学习后，总体成绩出现下滑的现象，从一定程度上反映出学生对几何知识的不适应。出现这种情况的根本原因是学生无法深入理解几何领域的核心概念。此外，教师对几何核心概念的教学过于技术化，体现几何核心内容特质的教学技术有待加强。

基于上述分析，笔者认为需要提出一种适应几何教学方式的概念教学，以促进学生对几何核心概念的理解，而举例便是一种让学生更好地理解和掌握数学抽象内容的手段。基于此，我们运用易良斌老师提出的“五例”教学法，即范例、正例、特例、反例、错例，以促进学生对几何问题的深度理解。

一、对“五例”教学法的基本认识

对“五例”的具体说明如下：范例，是指提供给学生学习用的样本例子、示范例子;正例是从正面说明命题、定义成立的例子;反例是从反面说明命题、定义不成立的例子;特例是位于特殊位置、特殊点、特定背景下的例子;错例是指学生经常犯错的例子，充分利用错例资源，激发学生积极参与。

要做好“五例”的教学，教师须站在理解数学的高度上，不但要对数学整个的知识体系有充分的理解，还要对数学传递给学生的文化有充分的理解，更要发挥数学在培养人的方面的作用。教师要以学生为主体，了解每个学生的最近发展区，因材施教，差异教学，让每一位学生都有所成长。教师不但要对教材的内容有充分的理解，还要能根据学生的实际情况对教材做一定的拓展，创造性地使用教材。

二、对“五例”教学法的价值分析

（一）正例，提升核心概念理解的严谨性

正例又称肯定例证，指包含着概念或规则的本质特征和内在联系的例证，本文指从正面论证论点的例子。正例是一种让学生更快更好地理解和掌握抽象数学内容的手段。教师应根据教学需要，选择和运用有效的、合适的例子来说明教学内容，以促进学生理解知识。

正例例证是非常有必要的。在数学中，有些公理、定理是不需要或者不必要进行直接证明的，但是有些定理只有进行了证明才能够让学生掌握。教材中也有很多定理的证明要求学生来完成，而学生的证明能力又非常有限，这个时候需要教师利用正例进行例证。

（二）反例，提升核心概念理解的辨识性

反例，又称否定例证。从反例的角度去分析，有利于发展学生思维的全面性和思维的深刻性，同时使其对整个概念的认识更清晰，能够快速地识别、辨别概念。数学中的一些命题，很难直接说明它的正确性，此时可举反例去论证。反例能增加学生思维理解的深度。

（三）错例，提升核心概念理解的深刻性

错例是一种重要的课堂生成性资源。错例能让学生的理解水平提高到更高层次，使其能够对概念有更为清晰的认识。错例可以是来自学生生成的，也可以是教师在教学设计时“有意而为之”的。教师要充分利用好错例，让学生从另一个角度加深对知识的理解。

（四）特例，提升核心概念理解的广阔性

特例在几何教学中有着广泛的应用。学生如果能够把特例弄清楚，就具有了把一些可研究的问题变为一般化的问题，或者把一般化的问题特例化的能力。

（五）范例，提升核心概念理解的直观性

范例是提供给学生示范用的例子。通过范例，学生能够明确地知道所要研究的内容，能够清晰地知道所要研究内容的来源。同时，通过范例支架的搭建，可以让学生对核心概念有更为直观的理解。范例是问题、建议等片段性支架根据某个主题的汇总和集合，它可以帮助学生对几何概念进行分析，完善推理过程，帮助学生积极思维。

三、“五例”教学法教学设计案例

“五例”教学设计主要有五个教学环节，即搭脚手架、进入情境、独立探索、合作交流、尝试运用，每个教学环节中都可能用到“五例”。下面以“浙教版”八下4.1“多边形（第1课时）”为例，突出“五例”在这一课时当中的教学实践。

环节一：搭脚手架。

本节的多边形知识是三角形相关知识的应用与推广，由三角形的概念类比可以得到四邊形的概念。教师要让学生知道：求四边形的内角和可以转化为三角形问题。这样可以为后续的多边形、特殊四边形（如平行四边形、梯形）等知识的学习做准备。同时，教师还应激发学生对数学问题中蕴含的内在规律进行探索的兴趣，培养与发展学生知识迁移的能力。因此，脚手架的搭建可以利用三角形的有关知识进行，而三角形便是多边形的一个特例。

环节二：进入情境。

问题1：出示学生自己制作的三角形、四边形、五边形的风筝。

师：同学们，这些风筝看起来是什么形状呢？它们是如何构成的？

教师通过学生自己制作的风筝，让学生回顾三角形的定义，从而据此推出四边形、五边形的定义。学生学习了多边形后，自然而然地能够理解“三角形、四边形、五边形等都是多边形的特例”。

环节三：独立探索。

在这一环节，学生需要用一种最为直观的方式验证猜测出的“四边形的内角和为360°”这一结论。于是有学生这样做：在一张纸上任意画一个四边形，剪下这个四边形的四个角，把它们拼在一起（四个角的顶点重合），可以看出这四个角构成一个周角。也有学生采用测量的方式，但是有一定的误差，在教师的引导下，用几何画板进行验证。

环节四：合作交流。

在环节1，通过特殊的拼图和几何画板的测量，学生猜测到四边形的内角和为360°，但是如何用数学的语言进行证明？在课堂教学中，教师进行适当的教学提示：能不能把四边形的知识转化为所学过的三角形的知识进行解决？教师先给出一个范例。学生从中受到了启发，懂得了转化思想在解决四边形的内角和问题中的应用。学生与学生之间相互交流，思维碰撞，也能用正例来证明四边形的内角和为360°。

环节五：尝试运用。

1.四边形风筝的四个内角∠A，∠B，∠C，∠D的度数之比为1：1：0.6：1， 求它的四个内角的度数。

分析：看到四个角的比例，这是利用了四边形的什么性质呢？学生很容易想到是利用四边形的内角和为360°。不妨设参数x，再根据四边形内角和为360°，得到关于x的一元一次方程，解得x，即得到四个内角的度数。

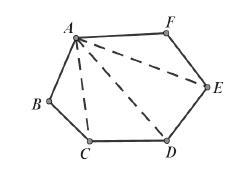
特例：探索六边形的内角和和外角和。

解：连接AC，AD，AE，得到△ABC，△ACD，△ADE，△AEF，从而得到六边形的内角和为720°，每个内角和相邻的外角构成一对平角，这些平角的和为1080°，平角的和减去内角和为360°，因此六边形的外角和为360°。

在教学过程中，“五例”教学并不是单独存在的，而是有机结合、互为支撑，组成课堂教学的五个部分，但使用的先后顺序可以根据实际情况进行调整。在“五例”教学中，对于一个概念而言，要达到更深层次的理解，正例、范例、反例、错例、特例往往可以综合使用。可以把“五例”应用于某个具体的教学片段，也可以在一个课时的教学中综合使用，对教师和学生对数学核心概念的深度理解起到积极的助推作用。

（责任编辑：韩晓洁）