立足“章首语”，教好“章引言课”

立足“章首语”，教好“章引言课”——以苏教版高中数学新教材为例石志群（江苏省泰州市教研室，225300）

摘要：苏教版高中数学新教材的章首语，是基于“章引言课”的基本构想（目标）设计的。由此出发，对章引言课的教学建议有：发现解决章首语提出的初始问题的问题链，得到本章内容框架;多角度认识章首语给出的基础结论，形成本章知识系统;联想章首语给出的类比对象，设计本章内容架构;运用章首语提出的思想方法，确定本章研究框架。

关键词：高中数学;章引言课;教材;章首语

传统的数学教学中，往往是一节课一个情境，使得数学内容之间缺少联系。比如，教学“三角函数”一章（主题或单元），由跳水中的旋转动作、钟表的校正等引入任意角，由角度制引入弧度制，由锐角三角函数引入任意角的三角函数……各小节（课时）的内容孤立地存在。其结果是学生的知识结构散点化，数学能力得不到有效提升，数学观念难以系统形成。

“章引言课”（基于主题或单元教学整体设计理念的教材中一章的起始课）的基本构想（目标）是：让学生在一章内容的学习之初，就能了解本章内容的背景，经历发现问题、提出问题的过程，明确本章内容的逻辑起点。在此基础上，经历概略性问题的解决过程，建构本章内容的整体研究背景、研究方法、知识体系以及价值观念、思想方法，从而促使学生全面、系统地认识本章内容。

苏教版高中数学新教材（2019年版）的章首语正是基于这样的构想设计的。引导学生认真研读章首语，从整体视角认识一章的知识结构，为本章的学习提供恰当的“先行组织者”，是非常有必要的。本文由此出发谈谈对章引言课的教学建议，以供参考。

一、发现解决章首语提出的初始问题的问题链，得到本章内容框架

有些章首语基于一定的现实背景，提出了本章初始的“大问题”（主问题）。通过对大问题的概略性研究，可以发现解决大问题的系列子问题（具有逻辑关系的问题链），由此可以得到本章的内容框架（研究的核心内容、目标定位）。这就是章引言课的基本形态。

例如，必修第二册第9章《平面向量》的章首语为：

冬天到了，大雪过后，白雪皑皑。如果你穿上滑雪板，站在被雪覆盖的、平滑的斜坡上（如图1），你会感到有一个力拉着你向下滑行。而且，斜坡越陡，这个力就越大，下滑的加速度也越大。

同样地，把木块放置在光滑的斜面上（如图2），木块将向下滑动。斜面的坡度越大，木块下滑的加速度也越大。

这些运动中含有哪些物理量？

用怎样的数学模型刻画这些物理量？

怎样运用这样的数学模型去解决问题？

通过对滑雪原型的物理模型（斜面上放置的木块）的受力、运动状态分析，可以得到力、加速度、速度、位移等物理量。通过对这些物理量的数学抽象，可以引出本章第1节内容——“向量概念”。

类比数量，可以确定第1节研究的主要内容：什么叫向量（概念）、相等向量（同一性标准）？向量之间有什么关系？……

数学对象，尤其是“量”（如数量），都能进行运算。而物理中的力有合力、位移有合位移……也就是说，向量也能进行运算。由此引出本章第2节内容——“向量运算”。

类比数量，以力、位移等为原型，从合力、合位移等可以概括出向量的加法、减法运算;由加数相同时的特殊加法想到相等的向量的加法，可以得到向量的“乘法”运算（数与向量相乘）;由数与数相乘想到向量与向量相乘，那么可以找到怎样的物理原型？由此可以建立怎样的向量乘法运算？

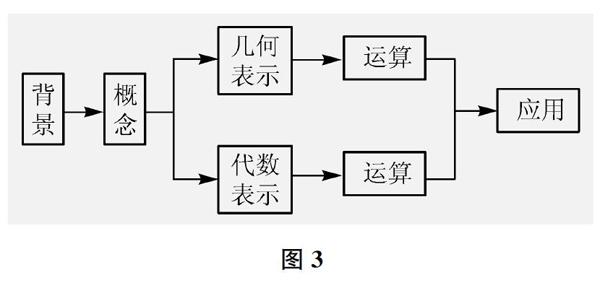
向量既有大小，又有方向，说明其除了几何特征，还有代数特征，那么如何用代数语言刻画（表示）向量？在这种代数语言下，向量的关系、运算如何刻画（表示）？这便是本章第3节内容——“向量基本定理及坐标表示”。

从向量的原型（来源）和向量的特征分析，向量可以在哪些方面有所应用？这便是本章第4节内容——“向量应用”。

……

至此，本章的知识体系自然形成了（见图3）。

与此同时，本章知识建构的方法也基本明确：通过对物理原型进行数学抽象，形成相应的概念、表示、运算等。

这里需要说明的是，因为只是概略性的研究，所以，框架中的内容不能过细，不能将后续具体内容的教學放在引言课上展开。要根据过程展开的需要确定研究到什么层次，例如“向量概念”中需要研究哪些内容是可以讨论的——如“什么是向量”“向量如何表示”“向量的同一性（相等向量）”“向量的关系”等内容，但这些内容具体是什么是不需要研究的。

二、多角度认识章首语给出的基础结论，形成本章知识系统

有些章首语基于一定的知识背景，给出了本章的基础结论（核心关系）。从不同的角度认识（推演）这一结论（关系），便可以形成本章的知识系统（具有逻辑联系、体现内在关联的一组知识内容及其结构）。这也是章引言课的基本形态。

例如，必修第一册第4章《指数与对数》的章首语为：

在初中，我们就知道了

a-n=1an（a≠0，n∈N）。

这样，指数幂的概念中，指数的范围就从正整数拓展到了负整数。自然地，我们想知道：指数幂中的指数的范围能否再拓展呢？

例如，a12有意义吗？

设想将整数指数运算aman=am+n（m、n∈Z）进行推广。

令m=n=12，得

a12·a12=（a12）2=a12×2=a=a12+12。

这说明，如果将a12看成一个数，那么它是a的平方根。用同样的思路，我们可以获得anm（m、n∈N，m≠0）的意义。

这样，我们将指数幂ab中指数b的范围从正整数推广到负整数、分数。

更一般地，

对一般的实数b，ab的意义是什么？

这一章首语给出了本章研究的核心问题（指数幂中的指数的范围能否再拓展）、基础结论（aman=am+n）以及研究案例和思路。由此出发，可以先看a13、a14、a15……（即分子为1的分数指数幂），就要知道什么叫3次方根、4次方根等，需要对“根式”进行推广。有了这样的基础，就可以对一般的分数指数幂进行意义建构，并进一步将指数b推广到一般的实数。既然当b为任意实数时，ab都有意义，那么，若ab=N，则b与a、N之间的关系是什么？——对数。

于是，本章的知识系统形成了（见图4）。

类似、相关地，必修第一册第6章《幂函数、指数函数与对数函数》的章首语如下：

等式23=8给出了三个数2、3、8之间的一种关系，用符号抽象后可表示为

ab=N。

在ab=N中，如果给定a、b、N中的两个数，那么ab=N就成为以另一个数为未知数的方程，如：

23=x，

x3=8，

2x=8。

对此，我们已分别学习了乘方、开方运算和对数运算。

进一步，在ab=N中，如果只给定a、b、N三个数中的一个数，那么ab=N就成为另两个数之间的“函数关系”，如：

x3=y，

2x=y，

2y=x。

上述x、y的关系中，可得到怎样的函数模型？

这些函数有哪些性质和应用？

这一章首语给出的本章研究的核心问题是由幂的关系式可以得到怎样的函数模型，基础结论是ab=N。

三、联想章首语给出的类比对象，设计本章内容架构

有些教学内容与之前的教学内容存在较强的相似性，如立体几何与平面几何、空间向量与平面向量。这些内容的章首语便给出了可以类比的学习对象。相应的章引言课便可以引导学生联想、类比对象，运用知识体系的内在关系，设计本章内容架构。

例如，选择性必修第二册第6章《空间向量》的章首語为：

在《数学（必修）第二册》中，我们学习了平面向量，研究了平面向量的运算、平面向量基本定理及平面向量的坐标表示，运用平面向量知识解决了数学和物理中的一些问题。然而，在现实生活中，许多涉及大小和方向的问题不仅出现在平面中，也经常出现在空间中。例如，吊车吊载物体，飞机降落，火箭发射……

空间向量是如何运算的？

怎样用向量解决空间图形的相关问题？

基于这一章首语，本章引言课的教学思路非常明确。平面向量中研究了哪些问题？平面向量有哪些应用？类比到空间向量，其知识架构自然就明确了：空间向量的概念、表示（几何表示与代数表示）、运算（几何形式与代数形式）、应用。平面向量可以用来研究平行、垂直等位置关系，求距离、角等数量，空间向量自然也要研究这些问题。于是，空间向量的内容架构就是将平面向量的相应内容“平移”过来。教学时，将这个“平移”过程交给学生就行了（具体过程不再赘述）。

四、运用章首语提出的思想方法，确定本章研究框架

数学的知识体系与其思想方法是密切相关的。有些章首语便提出了相关的研究思想方法，相应的章引言课便可以引导学生运用思想方法，获得研究思路，确定本章研究框架。

例如，必修第一册第3章《不等式》的章首语为：

在自然界和社会生活中，存在着大量的相等关系、不等关系、函数关系。我们曾经用等式（包括方程）刻画一些相等关系，用不等式刻画一些不等关系，用函数刻画一些函数关系，研究了等式、不等式、函数所具有的性质，并应用这些性质去解决问题。

在研究的过程中，我们看到，相等关系与不等关系是紧密联系的。例如，一元一次方程ax+b=0与一元一次不等式ax+b>0，在结构、性质、解法等方面就具有很大的相似性。

我们还看到，等式、不等式、函数之间也是紧密联系的。例如，一元一次方程ax+b=0、一元一次不等式ax+b>0与一次函数y=ax+b之间具有“统一性”：从函数观点看，一元一次方程ax+b=0的解就是一次函数y=ax+b的图像与x轴交点的横坐标，一元一次不等式ax+b>0的解集就是一次函数y=ax+b的图像在x轴上方部分的所有点的横坐标x所成的集合。

当然，我们还会遇到更多的、更一般的涉及不等关系的问题。面对新的问题，我们可以尝试利用上述解决问题的方法，去分析问题、解决问题。例如，

不等式具有哪些性质？

怎样从函数观点解决不等式、方程的问题？

基于这一章首语，本章引言课的教学要引导学生通过回顾反思的方式，从结构、性质、解法等方面研究一元一次方程、一元一次不等式及一次函数之间的关系，并由这种关系明确本章要研究的内容：等式研究了哪些内容？不等式是否要研究相应的内容？已经研究了哪些不等式？还可以研究哪些不等式？研究一元一次方程时运用的思想方法是什么？研究其他类型的方程是否可以运用这种思想方法？研究不等式问题是否可以运用这种思想方法？……最终，确定本章的研究框架。

参考文献：

[1] 任念兵.高中数学中观教学设计：现状、问题与对策[J].教育研究与评论（中学教育教学），2018（9）.

[2] 丁菁，刘明.新课标视角下的数学引言课教学——以“不等式”为例[J].教育研究与评论（中学教育教学），2018（6）.