复杂采空区充填开采对地面建筑的影响研究

2020-05-28刘焕春于建新焦华喆赵武胜

金属矿山 2020年4期

刘焕春于建新焦华喆赵武胜

（1.河南理工大学安全科学与工程学院，河南焦作454000；2.河南省地下工程与灾变防控重点实验室，河南焦作454000；3.中国科学院武汉岩土力学研究所，湖北武汉 430071）

深部采动覆岩移动规律与控制是采矿学科的基本研究内容之一，众多研究学者对岩层移动与地表沉陷规律进行了研究，取得了大量的研究成果[1-2]。金属矿山由于矿体的赋存状态及开采方法的特殊性，与煤矿地下开采存在较大不同[3-5]。任伟中等[6]通过地质力学模型试验，分析了在厚覆盖层条件下地表陷落特征随不同开采水平的变化规律。Villegas T等[7]将Kiirunavaara矿山开采引起的地表变形随时间的变化划分为3个阶段，并指出地表出现裂缝之前的应变扩展可能损害土木结构；并采用有限元和离散元软件分析了开采对上盘破裂位置、破裂角以及上下盘的稳定性[8]。王运敏等[3]研究发现地表沉降与水平移动具有较强的一致性，整体变化趋势具有阶段性的快速增加与趋缓的特点。崩落法上覆岩层冒落对于缓解深部开采高应力、保证足够覆盖岩层厚度、控制岩层移动具有重要作用。Xia等[9]通过实际监测得出程潮铁矿地下采矿引起的地表变形规律，与深部岩层移动密切相关。李庶林等[10]结合多通道微震监测、双力偶点源理论、地表深钻孔探测3种手段，得到了大红山铁矿采用无底柱分段崩落法开采不同时期高应力区、开裂带和崩落带的发展过程。宋许根等[4]依据实际监测结果，结合岩层移动机制，对塌陷发生以后不同时期、不同区域内的地表变形与扩展规律进行了分析，探讨了降雨对地表变形与岩层移动的影响。陆玉根等[5]认为金属矿山采用崩落法大规模深部开采后在地表形成了一个以裂隙为引导的塌陷区，明显存在崩落带和裂隙带，弯曲变形带不明显，但其岩层变形过程仍具有“三带”破坏特征。金属矿山地下开采引起的地表塌陷主要采用现场实测、数值分析和相似模拟等方法进行研究，取得了一定的研究成果，保证了矿山开采的安全。但对于地表存在需要保护建筑物的情况，是不允许具有较大塌陷和变形的。而在开展现场监测时，首先采用数值方法对岩体变形及沉降规律进行把握是极有必要和指导意义的。

江西省内某金属矿山采空区悬空面积大，地下空间复杂，矿柱分布不均，地表充填站位于采空区上方，一旦发生较大规模的矿柱崩塌、顶板大面积冒顶或上覆岩层的错动，将直接威胁地面建筑的安全，甚至造成重大灾害事故、产生严重的经济损失和恶劣的社会后果。因此，为保证矿山安全生产，本项目利用大型有限元分析软件ABAQUS对复杂采空区充填开采影响下的地表沉降规律以及充填站的稳定性进行研究。

1 工程概况

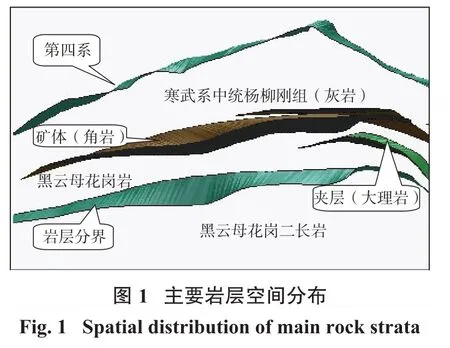
该金属矿山位于江西省境内，矿体赋存于燕山晚期细粒黑云母花岗岩体与杨柳岗组含炭硅泥质灰岩的接触带上，呈似层状、倒转置锅型产出，并随接触带产状的变化而变化，主要分布在0～24线间的1 200 m范围内。矿体埋深40～300 m，矿体及顶底盘围岩较稳定，水文地质条件简单，矿体岩层分布如图1所示。矿山采用地下方式开采，采用平硐开拓，铲运机装载，机车运输，采矿方法为留不规则点柱、条柱的全面法，类似于房柱法，采场静空跨度10～30 m不等，井下矿柱分布不均，部分顶板暴露面积过大，矿体回采多沿底板掘进，许多采空区顶部矿体残留，开采难度极大，为避免资源的浪费，合理安全有效地开采残余矿体，采用充填法对顶部残矿进行开采。地表充填站标高682.0 m，在10～12线之间，位于采空区上方，占地面积3 726 m2，充填站位置、采空区范围及矿柱分布如图2所示。

2 数值模型

2.1 修正Mohr-Coulomb理论模型

在描述岩土材料的强度特性和破坏行为方面，Mohr-Coulomb强度理论得到了广泛应用[11]。本项目采用文献[12]的修正Mohr-Coulomb模型，可以避免数值计算的发散和收敛的缓慢。

修正的Mohr-Coulomb屈服准则的表达式为

其中：

式中，σ1＞σ2＞σ3为主应力；c、φ分别表示黏聚力和内摩擦角；σm为平均应力为等效应力；J2、J3分别为应力偏量第二不变量和第三不变量；sx=σm-σy，sy=σy-σm，sz=σz-σm；θ为Lode角。

采用分段函数来描述K(θ)，具体表达式为

式中，

取θT=25°，|θ|≤θT时，在ρ平面屈服函数迹线不做处理，和经典的Mohr-Coulomb准则一致，而当|θ|＞θT时，对屈服函数的迹线进行光滑处理。

经过四十余年的发展，以氮肥为起点的云天化集团取得了令人瞩目的成就，同时也面临着国家宏观政策、安全环保形势、市场竞争环境、农业需求等诸多方面的变化与挑战。为了适应这些新变化、新挑战，云天化主动进行战略布局的调整，围绕“绿色科技服务现代农业”的理念，积极探索转型升级的新思路、新道路。

取塑性势函数与屈服函数的表达式一致，即：

式中，φ为膨胀角，其中K(θ)也与φ有关，表达式与屈服函数中的K(θ)类似。若φ=φ，则为关联流动；若φ≠φ，称为非关联流动，而当φ=0时塑性变形时材料的体积不发生变化。

2.2 三维模型建立

根据山体等高线和采空区内矿柱分布，建立10～12线间灰岩—矿体、矿体—花岗岩、采空区、矿柱的三维山体模型，如图3所示。计算模型长约400 m，充填站距左侧边界150 m，距右侧边界250 m；模型宽度范围为10～12线约100 m，模型底部高程为500 m，山顶最高处高程约790 m。采用四面体单元对计算模型进行离散，生成计算网格，模型共生成单元约90 000个。

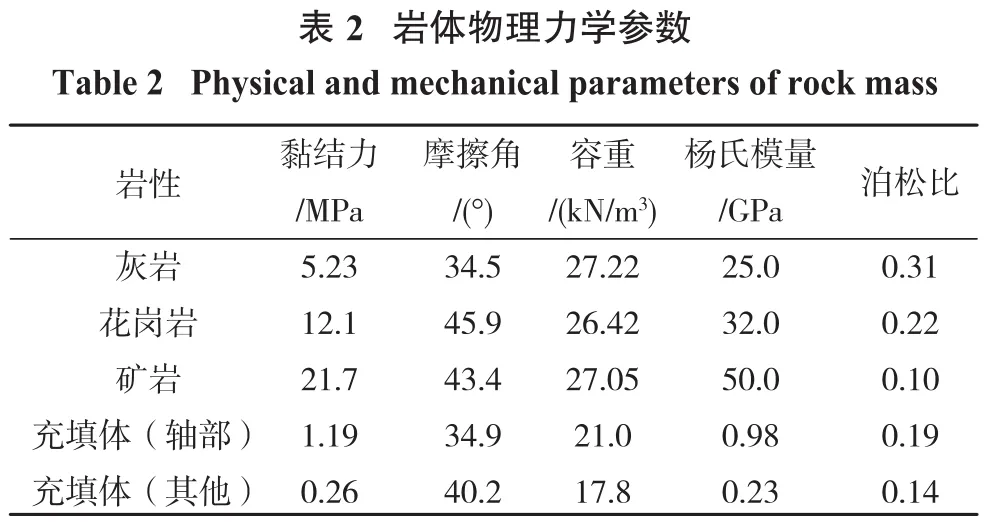
模型采用THM耦合4节点轴对称减缩积分单元，由于矿体开挖引起的位移主要是竖直方向位移，因此，在计算过程中，除山体上表面外，其余5个面施加法向约束。计算区域内矿柱的具体参数如表1所示，矿山岩体的物理力学参数如表2所示。

矿区地应力测试得到的最大水平主应力、最小水平主应力和垂直主应力随深度H（单位为m）的线性回归方程为

由于山体为不规则地表，无法通过常规方法施加地应力。为此，采用ABAQUS中子程序SIGINI通过编程进行施加，具体过程[13]如下。

根据山体表面的形状，拟合山顶标高方程，得到不同位置处山顶标高；根据山顶标高，得到不同位置处的埋深；根据地应力测试结果，计算得到该位置处的3个主应力；将主应力转化到局部坐标系中，在局部坐标系下施加初始应力。最终，山体内部形成沿着山体坡面方向分布的初始应力场，其中竖直方向上的正应力分布如图4所示。

根据矿体开挖及充填的顺序，数值计算共分5步：①地应力平衡，施加原岩应力，在岩体中形成原岩应力场；②底部开挖，根据矿体开挖顺序首先模拟底部矿体的开挖，预留矿柱；③底部充填，底部开挖完成后，对底部进行分层充填；④上部开挖，充填完成后，对上部矿体进行开挖；⑤采空区充填，上部矿体开挖完成后，对采空区进行充填。

3 模拟结果分析

计算结果中的符号说明：+表示应力为拉应力，位移与坐标轴同向，如在采场底板表示底鼓，顶板表示下沉，采场侧帮表示位移向采空区移动。-表示应力为压应力，位移与坐标轴反向。x方向代表平行于勘探线方向，y方向代表垂直勘探线方向，z向代表竖直方向。

3.1 岩体应力与位移变化

矿体开挖后，岩体主应力分布和位移变化如图5与图6所示。从图5中可以看出，开挖引起了山体应力调整，开挖充填完成后岩体几乎全部受压，在采空区顶板与矿柱出现了明显的应力集中，矿柱及顶板部位x方向最大拉应力均小于5.0 MPa。岩体中y方向应力较其他2个方向调整最小，但在矿柱部位出现了少量拉应力区。从竖直方向应力的分布可以看出，矿柱在竖直方向主要承受压应力，矿体开挖导致上覆岩层的应力向矿柱转移，矿柱承受了很大的竖向压应力，最大压应力达到了63 MPa。

从图6可以看出，矿体开挖后，在x方向（平行于勘探线方向）上部岩体向采空区移动，地表的变形表现为采空区左侧向右侧移动，x方向最大位移出现在采空区的左上方，最大位移量约6.2 mm。矿岩位移状态中，垂直位移比水平位移重要的多，因为过量的垂直位移将直接导致顶板的冒落，因此，该部分主要对顶板的垂直位移进行分析。在z方向（竖直方向），矿体开挖导致顶板下沉与底鼓，矿体顶板最大下降量约18.2 mm，充填在一定程度上减小了底鼓量，最大底鼓量约3.9 mm。

3.2 矿柱受力及变形分析

矿体开挖后矿柱受力如图7所示，矿柱受压缩变形如图8所示。在2个水平方向上，矿柱出现了拉应力，最大拉应力约1.2 MPa；在竖直方向上，矿柱主要承受压应力，且表现为采空区中部的矿柱受力大，采空区边界处的矿柱受力小，竖直方向最大压应力约63 MPa。由于山体与开挖体的不对称性，在矿体开挖过程中引起了矿柱的水平位移，但矿柱在2个水平方向上的位移量较小，最大水平位移量不足1.5 mm。由于上覆岩体向下移动、底板向上移动，矿柱竖向位移远大于水平方向位移，越靠近采空区中部、矿柱尺寸越小，矿柱的压缩量越大，最大竖向压缩量约15.58 mm。

3.3 地表变形规律

为了分析矿体开挖及采空区充填作用下地表的变形情况，以充填站为中心，布置如图9所示的A、B2类监测线，其中沿山坡方向布置 5 条（A-50、A-25、A0、A+25、A+50），相邻监测线间距25 m；在垂直山坡方向布置 7 条（B-60、B-40、B-20、B0、B+20、B+40、B+60），相邻监测线间距20.0 m。A类监测线上的位移变化如图10所示，B类监测线上的位移变化如图11所示。

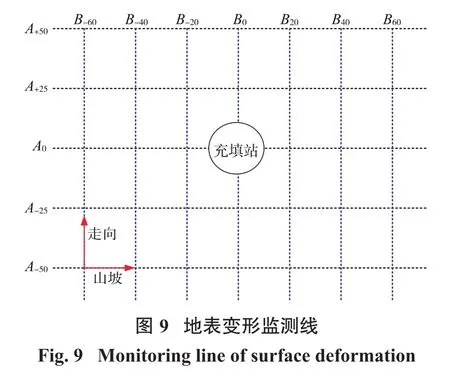
从图10可以看出，沿山坡方向，5条监测曲线上x方向的位移变化趋势相同。在充填站左侧（山脚侧）120 m的位置处，地表x方向位移接近于零；随着监测点靠近充填站，x方向的位移不断增加，监测站位置处x方向位移约为4.0 mm；地表x方向位移最大值约6.0 mm，出现在充填站右侧（山顶侧）40 m的位置。由于计算模型在y方向尺寸的限制，地表y方向的位移较小，最大约0.6 mm。沿山坡方向，在充填站左侧（山脚侧）120 m的位置处，地表z方向位移接近于零；随着监测点沿山坡向上，z方向的位移不断增加，监测站位置处地表z方向位移约为2.6 mm；在充填站右则120 m以后，地表z方向的位移趋于稳定，最大值约15.0 mm。

从图11可以看出，矿体开挖及采空区充填后，越靠近山脚，地表x方向的位移越小，越靠近山顶，地表x方向的位移越大。不同监测线之间，地表x方向的位移变化曲线基本一致。充填站处地表x方向最大位移约4.0 mm。由于计算模型在y方向尺寸的限制，充填站附近地表y方向的位移较小，最大约0.15 mm。矿体开挖及采空区充填后，地表z方向位移与x方向位移变化趋势相同。即：越靠近山脚，地表z方向的位移越小，越靠近山顶，地表z方向的位移越大。充填站处地表x方向最大位移约2.8 mm。