基于微型塌落筒和稠度漏斗的膏体充填料浆流变参数预测研究
2020-05-28裴佃飞宋泽普齐兆军姜海强吴再海
裴佃飞 宋泽普 齐兆军, 姜海强,3 吴再海
(1.山东黄金集团有限公司,山东济南250100;2.山东黄金集团有限公司充填工程实验室,山东莱州261441;3.深部金属矿山安全开采教育部重点实验室,辽宁沈阳110000)
随着矿山逐渐进入深井开采时代和绿色矿山理念的提出,充填采矿法在金属矿山生产中得到越来越广泛的应用,其中全尾砂膏体充填因其在技术和经济上的优势成为矿山充填的发展趋势。充填料浆的管道输送是全尾砂膏体充填的一个重要环节,而影响和决定其输送的一个重要因素是料浆的流动特性。全尾砂膏体料浆是一种非牛顿结构流体,流变学理论是研究其流动性能的有效手段,而屈服应力和塑性粘度是描述流体流变性质的关键指标,不仅直接决定着材料组分配比、充填系统设计,还影响着充填后膏体的机械强度。
目前充填料浆流变参数的测定主要依赖于实验室流变仪测试[1-2],而矿山现场不具备相应测试条件,因此其工程适用性较差。为了得到更为便捷的膏体料浆流变测试方法,国内外学者开展了大量的研究工作,得到了许多有益的成果。例如,Murate[3]通过研究新拌混凝土首次构建了塌落度与屈服应力圆锥塌落筒关系模型,之后Christensen[4]对该模型进行了修正;Pashias[5]构建了赤泥浆体的塌落度和屈服应力圆柱塌落筒关系模型;Clayton等[6]对圆锥塌落筒模型和圆柱塌落筒模型进行了试验验证,得出圆柱模型预测材料屈服应力的准确性更高;Tan[7]提出了微型塌落度测试膏体屈服应力测试程序,得到高度可重复的试验结果。郭亚兵[8]利用不同高度、不同直径的圆柱仪进行了对比试验,结果表明了塌落度试验所得到的屈服应力值与粘度计测定的精确屈服应力值吻合度良好;李亮等[9]依据圆锥塌落筒模型和圆柱塌落筒模型基础理论简化了模型计算公式。另外有相关研究采用V型槽测试自密实混凝土流动性能及采用Marsh漏斗测试粘稠液体流动性,通过流出时间度量评价[10-13]。然而,上述研究对象主要为水泥基充填料浆,尚未有针对采用C料作为胶结料的充填料浆的研究。目前,山东胶东半岛很多矿山为了降低充填成本、提高充填质量,普遍采用C料作为充填胶结料。此外。以往研究主要针对屈服应力,尚未有关于料浆塑性粘度的简单有效的测评方法。
鉴于上述问题,本研究采用2种不同微型塌落筒(锥形筒和柱形筒)测试料浆塌落度,结合流变测试结果确定最优塌落筒形状和尺寸,并在此基础上构建了无量纲塌落度—屈服应力关系模型。同时,鉴于V型槽及Marsh漏斗测试料浆流动性的适用性较差,采用自制稠度漏斗测试充填料浆流出时间,结合流变仪测试结果,构建料浆塑性粘度—流出时间关系模型。相关研究结果可以为现场充填料浆流变参数的高效准确评测提供一定参考。
1 试验材料
1.1 试验尾砂
试验尾砂为山东某金矿全尾砂,试验前进行脱水和烘干。采用激光粒度仪对其粒径分布进行测试,结果如图1所示。该尾砂-20 μm颗粒体积含量为25%,平均粒径176 μm,中值粒径为92 μm,不均匀系数Cu=24.08,曲率系数Cc=0.85,尾砂颗粒粗细差异较大,中间粒径颗粒缺少,级配不均。该尾砂比重2.65 g/cm3,比表面积3 470 cm2/g,物相组成比较单一,主要为石英和云母。

1.2 胶凝材料
胶凝材料为该矿山自主配制生产的胶凝材料,经测试该胶凝材料的比重为2.79 g/cm3,容重为0.97 g/cm3,其他性能参数见表1。

?
1.3 拌合水
试验所用拌合水为该矿充填用水,比重为1.03 g/cm3,pH值为7.9。
2 试验方案与试样制备
2.1 试验方案
(1)微型塌落筒优选。基于Murate锥形塌落筒模型和Pashias柱形塌落筒理论模型,通过对比分析不同形状尺寸塌落筒(见表2)测试试验料浆塌落度计算得到的屈服应力与流变仪测试结果,优选出最佳微型塌落筒。试验料浆质量浓度分别为70%、72%、74%、76%、78%、80%,灰砂比分别为1∶4、1∶10、1∶15、1∶20。

?
(2)料浆流变参数和流出时间测试。采用最优微型塌落筒和自制稠度漏斗测试上述不同配比料浆塌落度和流出时间,结合流变仪测试得到的料浆流变参数(剪切屈服应力和粘度),构建屈服应力—塌落度和塑性粘度—流出时间关系模型。
2.2 试样制备
搅拌前,先将称量好的尾砂和胶凝材料手动混合均匀,然后加入拌合水利用NJ-160型搅拌机进行搅拌,搅拌具体流程为:低速(转速140 r/min)搅拌120 s,停15 s之后高速搅拌(转速258 r/min)120 s停机,最后将料浆转移至烧杯中进行流变测试。
3 测试方法
3.1 流变测试
采用Brookfield RSR-SST流变仪,配备VT-40-20型浆式转子(φ20 mm×40 mm)。采用控制剪切速率模式(CSR)进行流变参数测试,具体测试流程为:以100 s-1的剪切速率恒定剪切100 s;随即在100 s内剪切速率匀速降低至0 s-1,如图2所示。
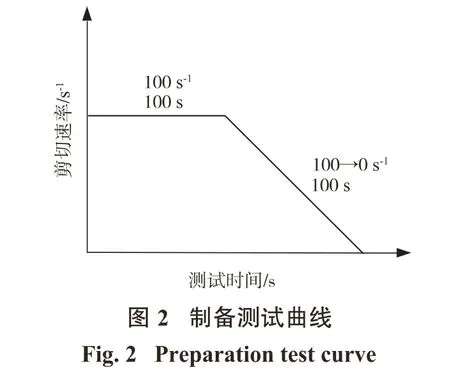
基于测试的料浆流动曲线特点,采用Herschel-Bulkley模型(见式(1))对流动曲线进行拟合,得到料浆的流变参数。

式中,τ为剪切应力,Pa;τ0为屈服应力,Pa;η为塑性粘度,Pa·sn;γ为剪切速率,s-1;n为流变指数。
3.2 塌落度测试
采用4种不同形状尺寸的微型塌落筒进行试验(如图3所示),具体形状尺寸参数见表2。试验前先用湿布润湿试验平台和塌落筒,之后将塌落筒放置于试验平台中心,参考ASTM C143混凝土塌落度标准试验程序,将制备好的料浆分3次倒入塌落筒,每次倒入塌落筒1/3体积料浆,用捣棒适当捣实、刮平,随后垂直均匀提起塌落筒,等待3 s后对料浆塌落高度进行测量。
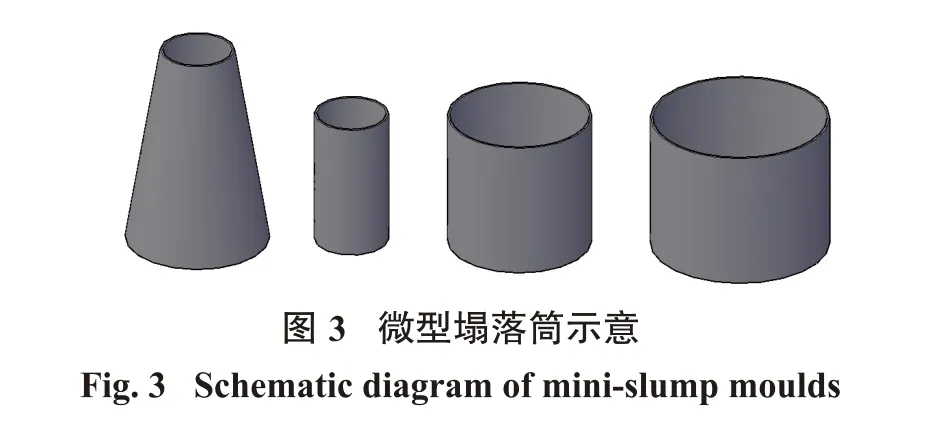
3.3 流出时间测试
由于目前没有专门针对充填料浆流出时间的测试装置和方法,基于充填料浆的特有性质,本试验采用自制漏斗进行流出时间测试(如图4所示)。测试前将漏斗调整水平,封闭底口,将制备好的料浆均匀倾入漏斗内,直至料浆装满漏斗并刮平(料浆体积1 725 ml左右),开启底口,使浆体自由流出,记录浆体全部流出的时间t。

4 结果与分析
4.1 塌落筒形状与尺寸影响
试验采用不同形状尺寸的塌落筒进行测试,且不同料浆的物理性质不同,为了统一对比不同坍落度值和屈服应力值,将测试得到的塌落度和屈服应力无量纲化。无量纲变量定义如下:

式中,h'为无量纲塌落度;h为测试坍落度,mm;H为塌落筒高度,mm;τ'为无量纲屈服应力;τ为流变仪测试屈服应力,Pa;ρ为料浆密度,g/cm3;g为重力常数;H'为料浆高度,mm。
试验得到无量纲屈服应力和无量纲坍落度关系如图5所示。

由图5可知,对于柱形塌落筒,当无量纲屈服应力在0~0.2之间时(无量纲塌落度大于0.25时),不同柱形塌落筒的测试结果相近,且通过Pashias柱形模型计算结果与流变仪测试结果相关性较好,其中柱形2#塌落筒测试结果与Pashias柱形模型相关性最优;当无量纲屈服应力大于0.2时,柱形3#塌落筒测试得到的屈服应力略小于柱形2#塌落筒的测试结果,但差距不大,而柱形1#塌落筒测试结果与前两者比较偏小,相比于流变仪测试结果,Pashias柱形模型计算值偏小。对于锥形塌落筒,其测试结果相比于柱形塌落筒测试结果及Murate锥形模型计算结果都要偏大,且锥形塌落筒测试结果与Murate锥形模型计算结果偏差较大。
由试验数据看出柱形塌落筒对料浆屈服应力的测试精度要优于锥形塌落筒,这与相关学者的研究结果试一致[6-12]。通过对比不同高径比柱形塌落筒测试结果,高径比为1.49(柱形1#)时不同配比料浆测试结果稳定性较差,因为太大的高径比会导致料浆圆柱体的坍塌而不是流动,同时,柱形塌落筒太小的高径比将导致料浆圆柱体仅有小程度的塌落,从而使屈服应力值测量范围很小。
由于屈服应力和塌落度是在无量纲处理后进行对比的,因此塌落筒的高度会对试验结果产生影响。有关研究认为塌落筒高度的增大可以提高料浆屈服应力测试精度,参考Clayton[7]的研究结果,当柱形塌落筒的高度为75 mm、102 mm、120 mm时(高径比1),塌落筒测试屈服应力结果和流变仪测试屈服应力结果出现偏离的应力值分别为250 Pa、350 Pa、500 Pa,当柱形塌落筒高度为200 mm时,塌落筒测试结果与流变仪测试结果无偏差,但试验用料量较大(6 280 ml)。矿山膏体充填料浆质量浓度一般小于等于76%,对应的屈服应力不大于350 Pa。
综合测试精度、材料用量因素,尺寸为φ100 mm×100 mm的柱形塌落筒为最优形状尺寸。
4.2 屈服应力—塌落度关系模型
基于柱形2#塌落度筒测得无量纲塌落度和对应无量纲屈服应力数据进行拟合,得到屈服应力—塌落度关系模型如下:

该拟合的残差平方和为0.003 37,相关系数为0.963 9,拟合参数的标准误差分别为0.053 04、0.048 34、0.013 48,说明拟合效果良好。为了进一步验证该模型的可靠性,对灰砂比1∶4,质量浓度70%、72%、74%、76%、78%、80%的料浆进行塌落度测试,利用式(4)计算得到相应的屈服应力,并与流变仪测试结果进行对比,结果如图6所示。由图6可知,当试验料浆质量浓度不大于76%时,通过式(4)计算的料浆屈服应力与流变仪测试的屈服应力基本吻合;当料浆质量浓度为78%、80%时,拟合公式计算值明显偏离流变仪测试值,且料浆质量浓度越大,测试结果偏差越大。上述结果表明本模型适用范围为0~0.1无量纲屈服应力料浆。

4.3 料浆塑性粘度测试
不同浓度和灰砂比料浆的粘度和相对应的流出时间关系如图7所示。可知,当料浆质量浓度一定时,随着灰砂比的降低,料浆塑性粘度增大,料浆骨料尾砂粒径分布不均匀,-20 μm含量达到25%,形成的料浆较致密,塑性粘度大,添加胶凝材料填充了料浆的空隙,并使料浆中的游离水转化为包裹尾砂颗粒的结合水,减小了尾砂颗粒之间的摩擦,相当于起到了润滑的效果,料浆更加均匀,使得料浆塑性粘度减小。相同质量浓度时,随着料浆灰砂比的改变,料浆流出时间与其塑性粘度呈负相关关系。当料浆质量浓度增大,其塑性粘度随料浆质量浓度的变化规律性不强,但料浆的流出时间急剧增加,当质量浓度增大到78%时,料浆已经不能流出测试漏斗。
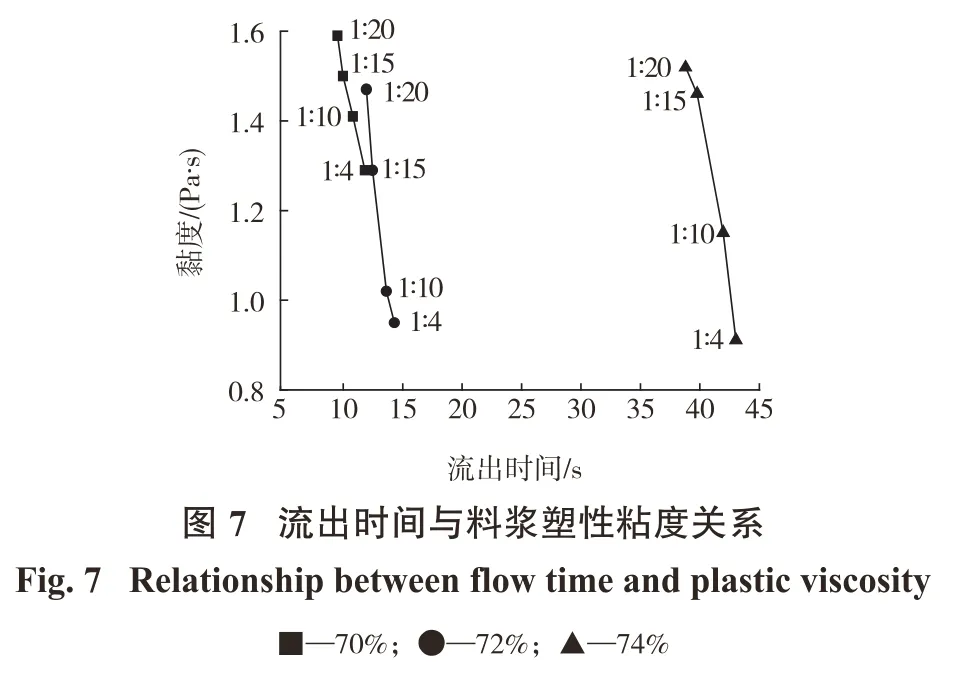
基于上述分析可知料浆流出时间随质量浓度与灰砂比变化的大致趋势,但通过此次试验料浆塑性粘度与其流出测试漏斗时间关系的规律性不强,这与试验操作误差及数据处理流变模型的选择也有一定关系,有待进一步研究。
5 结 论
通过一系列试验探索了膏体充填料浆塌落度—屈服应力和流出时间—塑性粘度间的关系,主要得到如下结论:
(1)圆柱微型塌落筒相对于圆锥微型塌落筒能更准确评测料浆屈服应力,柱形塌落筒的最优尺寸为φ100 mm×100 mm。
(2)基于柱形塌落筒构建了无量纲屈服应力—塌落度关系模型,该模型适用范围为无量纲屈服应力值在0~0.1的料浆。
(3)尝试探索了充填料浆塑性粘度与流出测试漏斗时间的关系,结果表明相同质量浓度时,随着料浆灰砂比的改变,料浆流出时间与其塑性粘度呈负相关关系;当料浆质量浓度增大,其塑性粘度随料浆质量浓度的变化规律性不强,有待进一步调整测试工具和方式进行系统测试。
