基于横向安全距离模型的主动避障算法
2020-05-28胡朝辉黄顺霞杜展鹏高鹤萱
胡朝辉,黄顺霞,杜展鹏,郭 星,高鹤萱
(1.湖南大学,汽车车身先进设计制造国家重点实验室,长沙 410082; 2.湖南湖大艾盛汽车技术开发有限公司,长沙 410000)
前言
主动避障系统能实时监测行车安全状态,及时提供安全警告和操作控制,达到规避危险的目标,提高行车主动安全性。目前,主动避障算法主要基于纵向安全距离模型建立,未考虑移动目标的横向运动特性。因此,本文中以横向移动目标为研究对象,建立一种横向安全距离模型,并提出一种基于横向安全距离模型的主动避障算法。
安全距离模型是避障系统功能实现的基础,主动避障系统中用于研究或实际应用的安全距离模型,大多基于传统的3大类安全距离模型,即基于车辆制动过程的安全距离模型、基于车头时距的安全距离模型和驾驶员预瞄安全距离模型。文献[1]中以“碰撞时间倒数”为评价指标,建立了基于危险系数的分级安全距离模型,具有较好的驾驶员特性。文献[2]中以控制车辆最小安全距离为最终目的,针对不同工况提出具体的估算模型,得出了一种最小安全车距控制模型。文献[3]中考虑了路面附着系数、坡道角等因素,提出改进的安全距离模型。文献[4]中融合了基于制动过程和车头时距的安全距离算法,根据速度阈值选取距离模型。然而,上述安全距离模型中没有考虑移动目标的横向运动特性,对于横向移动目标的主动避障存在一定的局限性。
本文中利用横向移动目标的横向相对位置和速度修正避障距离,建立横向安全距离模型;在车辆对外界环境感知信息的基础上,根据横向安全距离模型判断行车状态,完成主动避障算法设计。本文中提出的避障算法还包括以下功能:(1)能够实时监测移动目标的停留情况,降低移动目标随机移动特性对避障性能的影响;(2)能够根据路面峰值附着系数设定最大制动减速度,充分利用当前行驶路面避障,并适时调整制动控制强度,以适应不同路况的主动避障行驶。
1 实时路面附着系数估算
路面附着系数的估算方法主要有Cause-Based[5]和 Effect-Based[6-7]两类。Cause-Based主要利用加装传感器测量路面类型参数和路面状态参数,通过估算模型获取路面附着系数,具有一定的预测性,但成本高,使用条件限制大。Effect-Based根据路面变化引起的整车响应估算路面附着系数,主要是基于轮胎响应或基于车辆动力学响应,成本低,适用范围广,鲁棒性好等,对主动安全系统发挥着重要作用[8]。本文中基于Effect-Based,利用车辆动力学响应特性,根据获取的本车状态参数,估算路面附着系数。
假设行驶路面平直,采用1/4车辆模型作受力分析(见图1)。
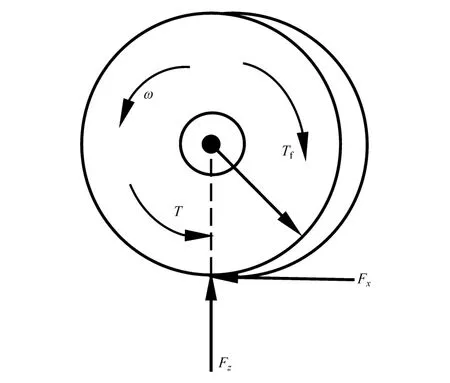
图1 1/4车辆模型

根据附着系数的定义式:

整理式(1)和式(2),可得当前行驶路面的附着系数:

式中:Fx为地面纵向反作用力(制动时为负);Fz为地面法向反作用力;J为车轮转动惯量;Tf为车轮滚动阻力;ω为车轮角速度;T为驱动力矩(制动时为负);R为车轮滚动半径。
2 横向安全距离模型
根据车辆传感器实时获取移动目标横穿马路的相对位置、速度,预估移动目标在横穿马路的时间段内车辆是否可达其目标位置,建立安全距离Dd:

式中:H为车道宽度;v0为横向移动目标横穿马路的横向速度;v车为自车行驶速度;D0为安全间距。在不采取避障制动措施的条件下,保证移动目标安全通过后,自车距移动目标的最小纵向间距如图2所示。
避障时,满足车辆自身的制动约束条件,建立避障系统的制动距离Ds:

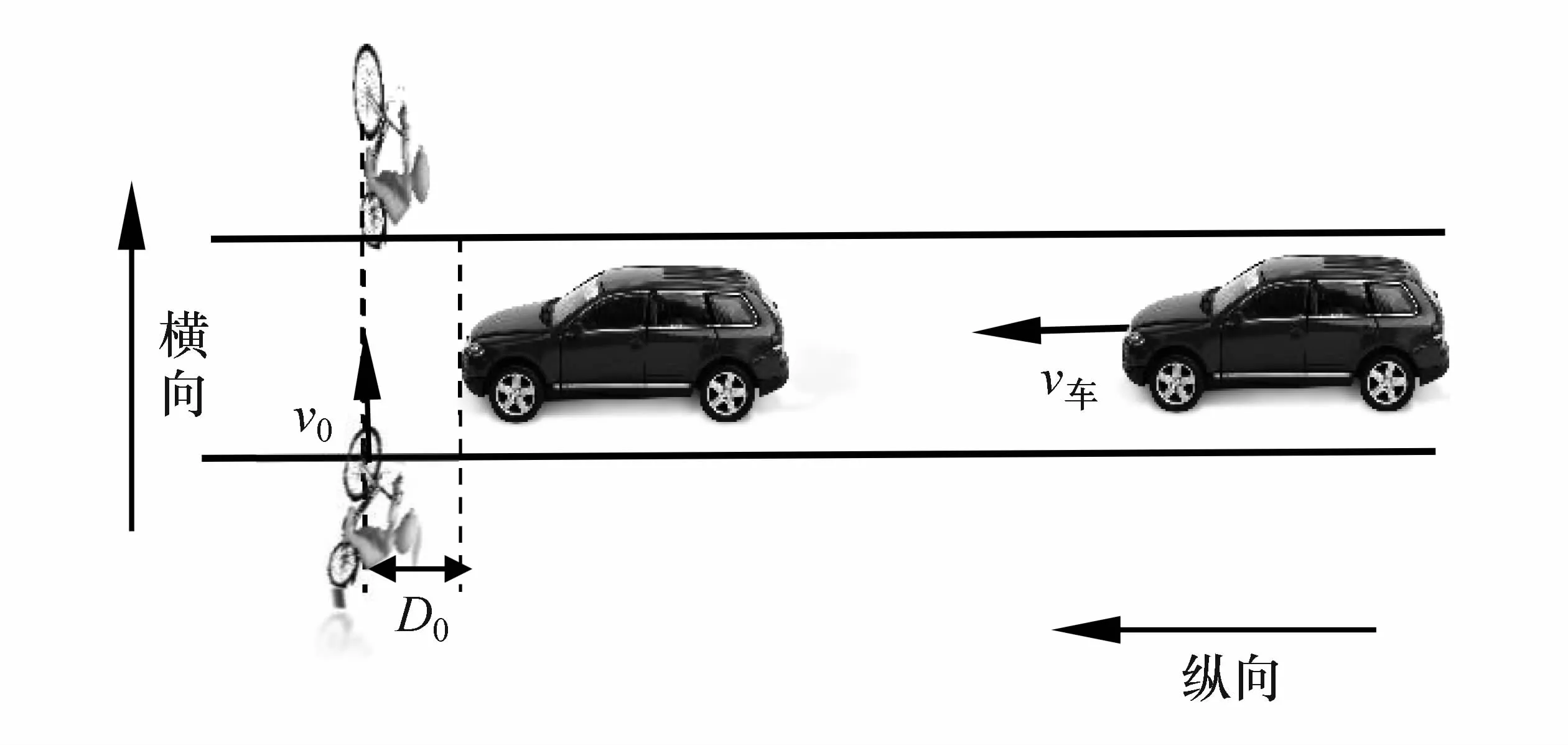
图2 横纵向示意图
式中:a车为自车减速度;d0为最小保持间距,在采取避障制动措施的条件下,保证移动目标安全的最小纵向间距。
根据安全距离Dd、制动距离Ds建立横向安全距离模型,安全距离Dd决定避障系统制动切入时机,制动距离Ds决定避障系统施加的目标制动减速度。
3 主动避障控制策略
3.1 避障逻辑
避障逻辑部分利用建立的横向安全距离模型计算阈值Dd、Ds,判断行车危险状况,实现避障系统的分级处理。
根据车载传感器获取的信息,判断本行车道内是否存在横向移动目标,不存在时保持当前状态行驶;存在时,须根据横向安全距离模型计算的阈值Dd、Ds,判断检测获取的间隔距离D是否可保障横向移动目标安全穿越马路,当D>Dd,即满足行车安全时,继续以当前状态行驶;否则表明间隔距离D不能满足横向移动目标安全穿越马路的需求,避障系统进一步根据间隔距离D与阈值Ds的关系,采取相应的制动措施;满足D≤Ds时,避障系统控制车辆进入紧急制动工况,车辆以最大制动减速制动;否则控制车辆进入减速工况,以舒适减速值减速行驶。其避障逻辑流程图如图3所示。
3.2 减速度
检测到目标对象时,避障系统依据安全距离模型计算的阈值确定目标减速度,控制相应执行器完成避障。避障过程中,施加适应于当前行驶路面的目标减速度,不仅可提高避障的效率,且也会提高驾驶舒适性。
制动过程中,地面制动力FXb、制动器制动力Fμ与地面附着力Fφ满足图4所示关系:

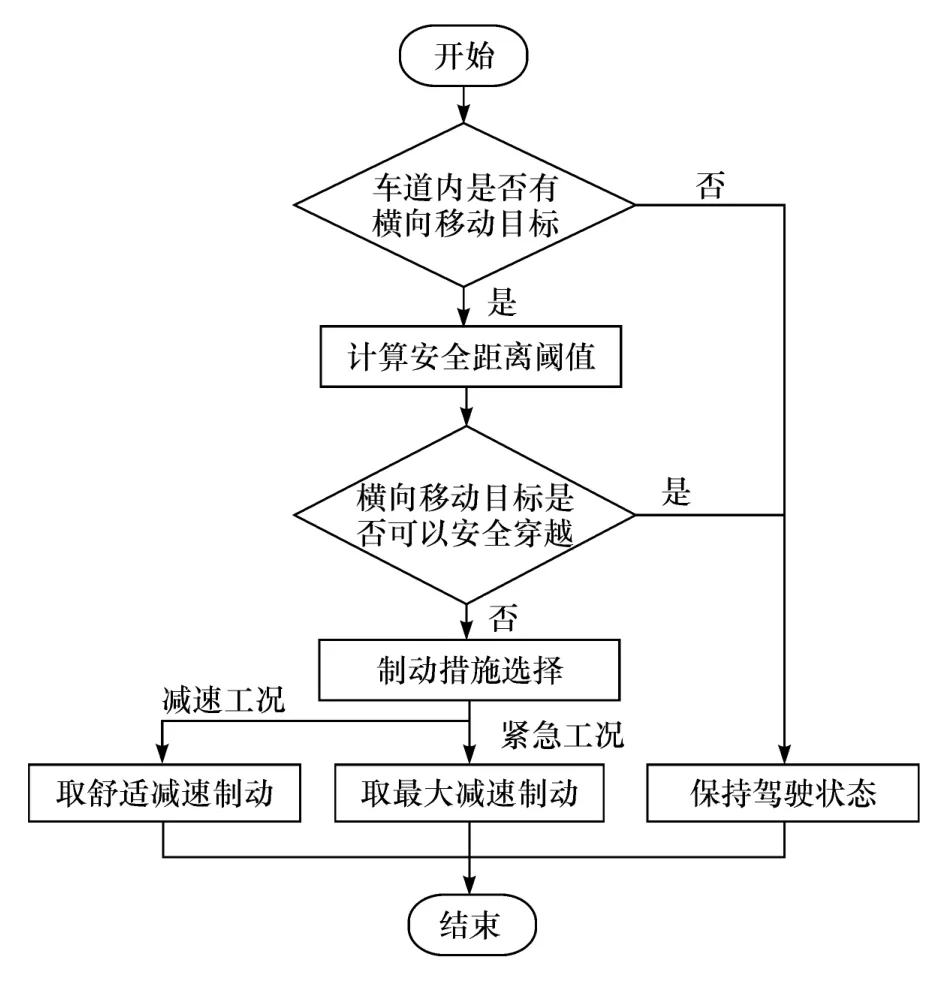
图3 避障逻辑流程图
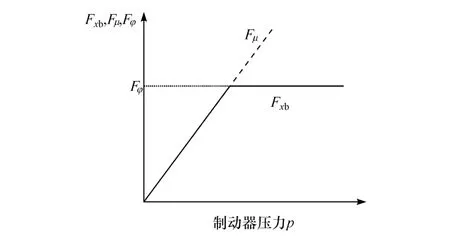
图4 FX b、Fμ、Fφ关系曲线
故制动时,制动减速度a车受路面条件约束,满足

式中:G为汽车重力;μmax为行驶路面的峰值附着系数;g为重力加速度。
3.2.1 舒适减速度
当避障系统进入减速工况时,要求以目标减速度控制车辆减速避障,在保障移动目标安全横穿马路的基础上,提高自车行驶舒适性。
文献[9]中调研了北京、上海、广州、武汉、重庆和汕头6个城市的汽车行驶工况,各行驶工况下最大减速度统计值如表1所示。文献[10]中分析125名驾驶员在正常行车中的经验数据,获得98%的驾驶员行车减速度不会超过-2.17 m/s2,而当减速度达到-3~-4 m/s2时会引起人体的不适。本文中将主动避障在减速行驶时的舒适减速度设为-2 m/s2。
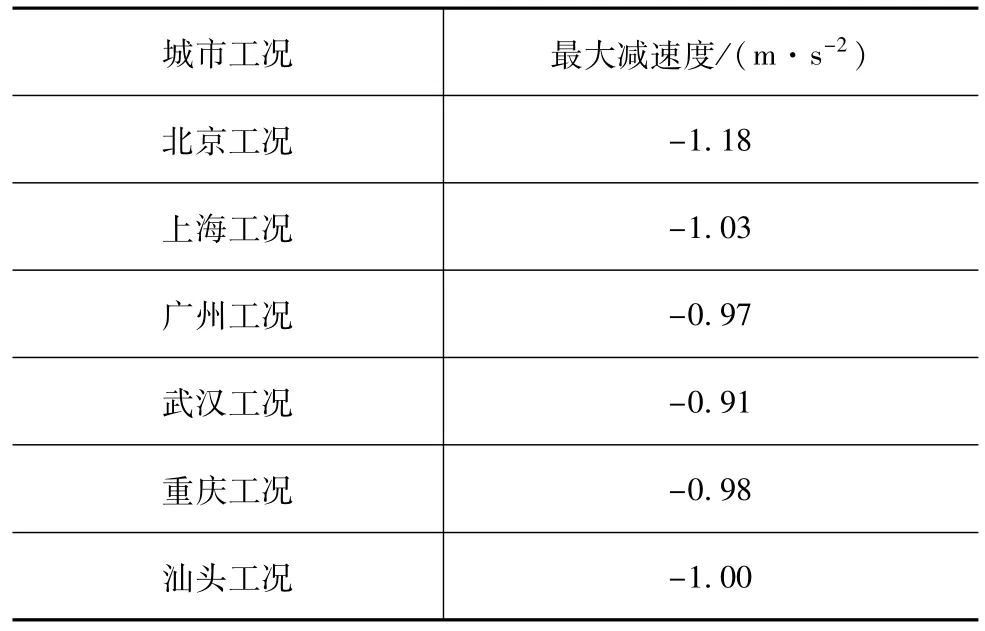
表1 6种城市行驶工况下最大减速度统计值
即间隔距离 D满足 Ds<D≤Dd时,取 a车=-2 m/s2作为减速行驶的目标减速度,实现减速工况下的主动避障行驶。
3.2.2 最大减速度
当避障系统进入紧急制动工况时,要求以当前行驶路面的最大减速度为目标减速度制动,以获取最大地面制动力,即a车=μmaxg。
利用行驶路面与Burckhardt轮胎模型在典型路面相似度的特征值来估算当前行驶路面的峰值附着系数[11],其定义为

式中:μ1max、μ2max分别为所选 Burckhardt轮胎模型中两条典型路面的峰值附着系数;μ1、μ2分别为所选Burckhardt轮胎模型中两条典型路面在当前滑移率所对应的附着系数;α、β为相似特征值。
式(8)~式(10)满足:

其仿真结果表明,路面峰值附着系数的估算误差控制在5%左右。本文中利用该辨识算法,估算当前行驶路面的峰值附着系数。
由式(3)可获取当前行驶路面的附着系数μ,根据车轮滑移率定义式可估算当前行驶路面的滑移率s。
制动时,滑移率s满足

驱动时,滑移率s满足

根据当前行驶路面的滑移率、附着系数,选取两条相似Burckhardt轮胎模型中典型路面的μ-s曲线,根据式(8)~式(10)和式(13)估算当前行驶路面的峰值附着系数,其估算模型如图5所示。
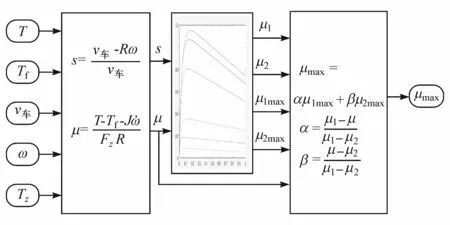
图5 路面峰值附着系数估算模型
即间隔距离D满足D≤Ds时,车辆进入紧急避障工况,根据当前行驶路面的估算峰值附着系数获取最大制动减速度a车=μmaxg,实现紧急避障工况下的主动避障行驶。
3.3 避障策略算法
横穿马路的移动目标参与交通的随机性强,考虑到横穿停留等不确定因素,在避障策略中加入移动目标的停留检测,当移动目标停留马路时,避障系统直接进入制动状态的判断,加快系统响应,以确保横向移动目标的安全。
考虑不同季节天气影响的多变行驶路况,避障减速工况的舒适减速度可能不满足当前行驶路面附着条件,如在附着率低的冰雪路面减速避障。在避障策略中引入制动强度的判定,根据估算的路面峰值附着系数,判断避障逻辑分级处理获取的制动减速度值是否满足当前行驶工况制动强度的要求,适时调整制动强度,提高避障行驶安全。
围绕避障逻辑,加入停留检测及制动强度判定,制定整车主动避障策略算法,其系统整体架构如图6所示。
4 验证与结果分析
骑行者横穿是一种典型的横向交通模型,本节将骑行者作为横向移动目标,验证本文提出的基于横向安全距离模型主动避障算法的有效性。
4.1 搭建仿真工况
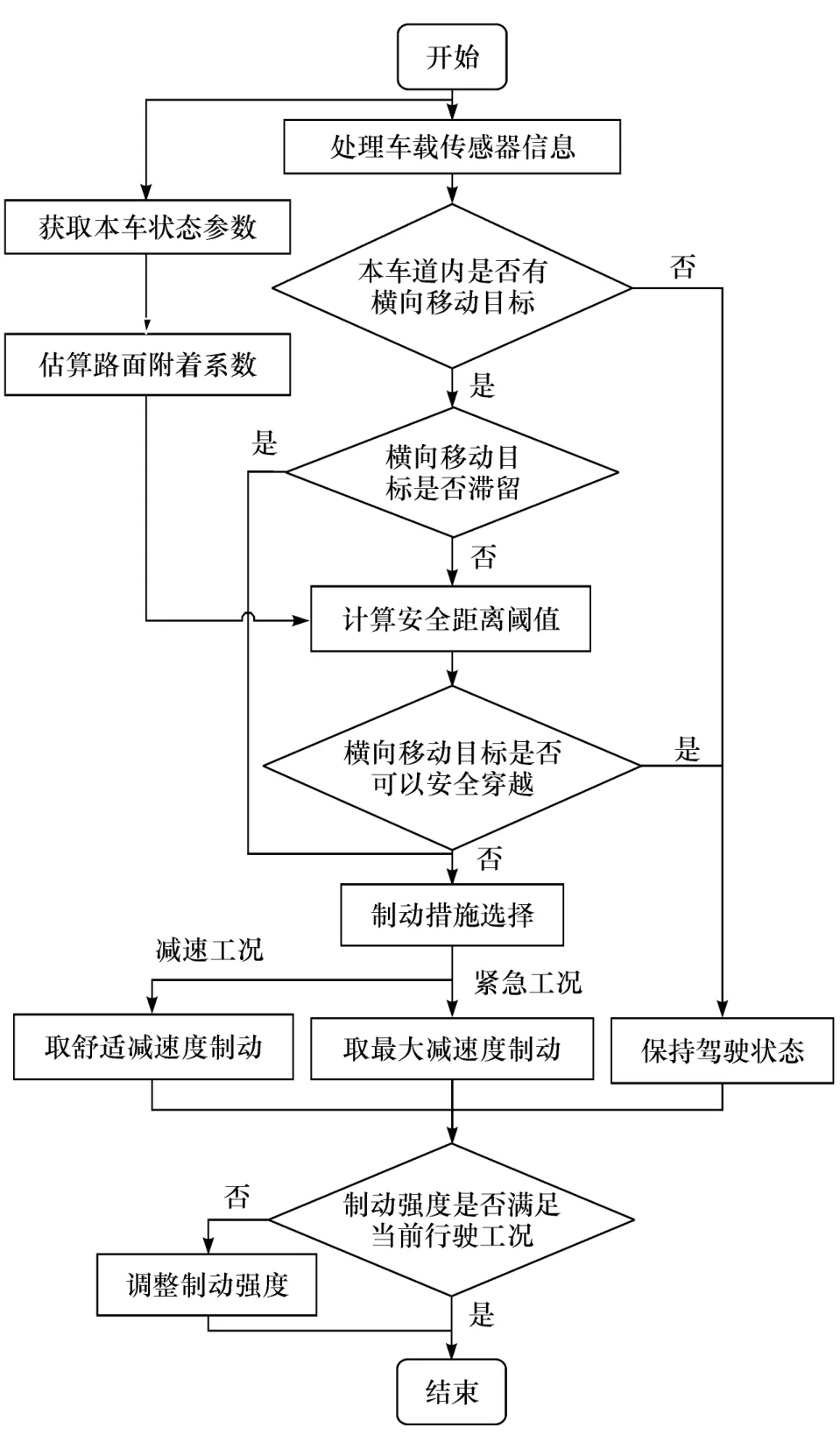
图6 系统整体架构
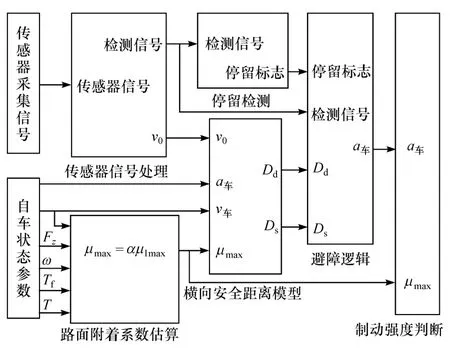
图7 避障策略模型
基于Simulink模块搭建避障算法模型,如图7所示。该模型主要由信号处理、路面附着系数估算、横向安全距离模型、停留检测、避障逻辑处理和制动强度判断等模块组成。信号处理模块主要处理避障控制系统的输入量,主要是对传感器采集信号和本车状态参数的滤波处理;路面附着系数估算模块根据估算算法完成当前路面峰值附着系数的估算;横向安全距离模型依据信号处理模块输出量计算避障判断阈值;避障逻辑处理模块根据预设避障逻辑判断行车危险状况,实现避障系统的分级处理,获取避障目标减速度;停留自检模块主要负责监测移动目标横穿马路的状态;制动强度判断模块修正低附着路况的制动强度,提高避障行车安全。
为预测、仿真车辆对外界环境的感知和车辆的碰撞检测,在PreScan中构建仿真场景,获取横向移动目标在模拟交通场景中的检测信号及自车的操纵(转向、制动、加速)响应量。基于 PreScan自带的AEB系统示例构建仿真场景,为满足碰撞场景,在EuroNCAP_AEB_VRU_nearside_adult示例基础上,将Actors中对象Human Textured改换为Cyclingcyclist,并将 Cyclingcyclist的 Speed Profile加入 1.5 s的延时,修改自车Objectcon figuretion中的 control项,加入本文避障算法,传感器模型等设置参数与EuroNCAP_AEB_VRU_nearside_adult仿真示例保持一致。打开Simulink仿真模式,完成PreScan与Simulink联合仿真连接,在自车模型中加入避障策略模型,建立PreScan与Simulink的联合仿真。
为获取路面附着系数估算模块所需的本车状态参数,根据PreScan Actors中添加的车辆类型,设置CarSim仿真页面的车辆参数和仿真工况,建立Car-Sim与Simulink联合仿真,将估算模块所需的自身状态参数导入Simulink控制模型,并将模型输出的操纵控制量导入CarSim仿真,更新车辆行驶状态参数。
在 Simulink中完成 PreScan/Simulink/CarSim联合仿真模型的连接,如图8所示。
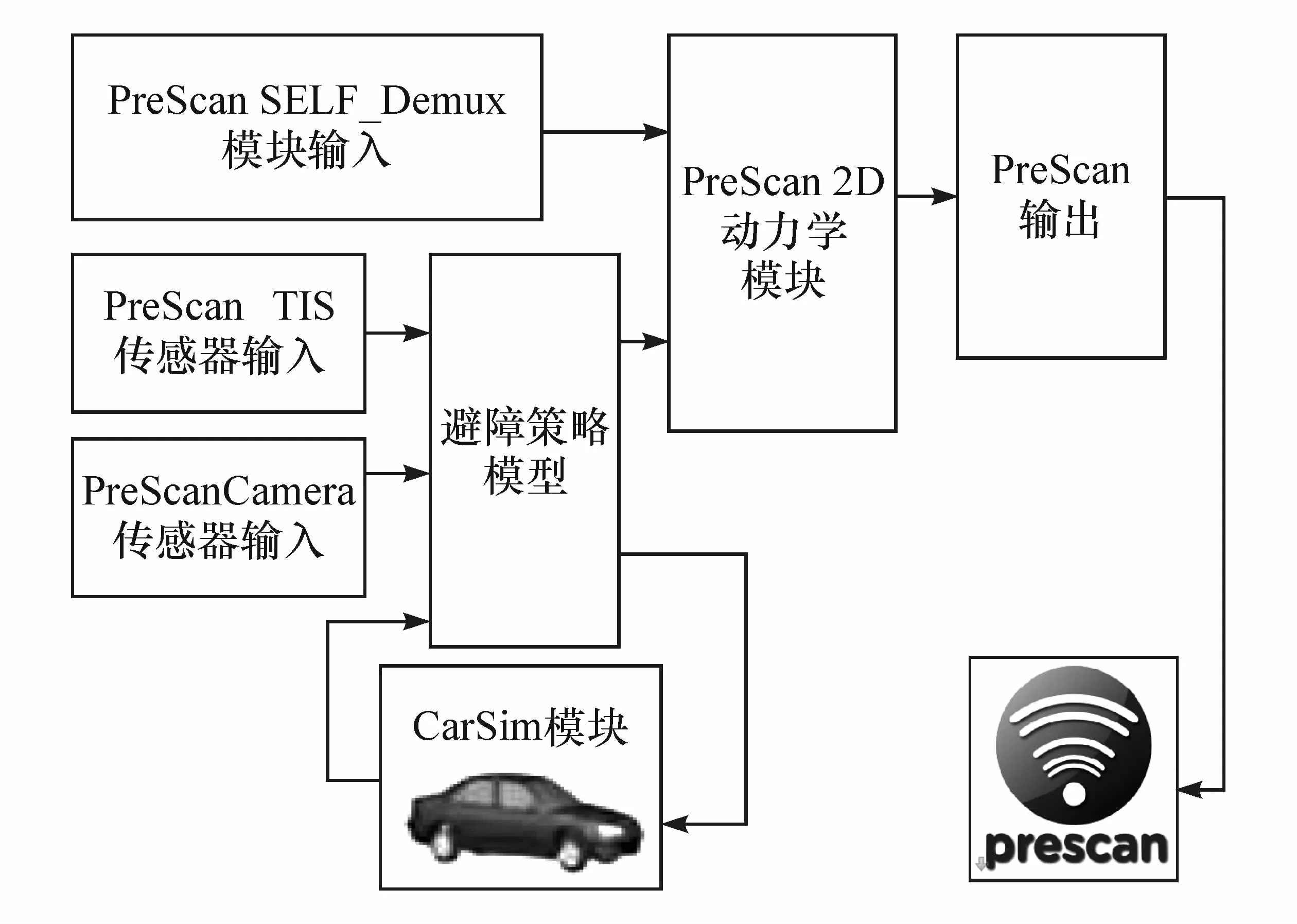
图8 联合仿真模型
4.2 仿真结果分析
构建仿真场景中,自车以15 m/s的速度在车道内直线匀速行驶,1.5 s后,骑行者以4.5 m/s横穿马路,若不采取制动措施,在5.36 s时发生碰撞,运行过程中,自车的速度、减速度曲线如图9所示。
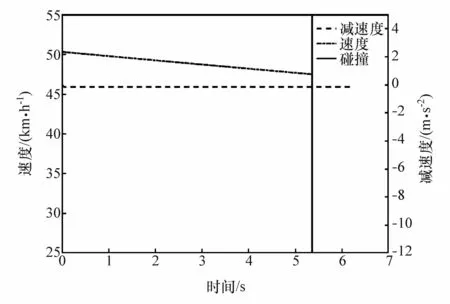
图9 无避障控制下自车的速度、减速度曲线
在仿真模型中加入主动避障算法,仿真结果显示:本车以15 m/s的速度在车道内行驶到4.84 s时,检测到横向穿越马路的骑行者,车辆进入紧急制动状态。运行过程中,自车的速度、减速度曲线如图10所示,自车的制动压力值如图11所示,图12为D、阈值Ds和Dd关系曲线。由图可见,当t=4.84 s时,Ds=13.54 m,Dd=13.93 m,D=7.01 m,根据避障算法可知,在4.84 s时,间隔距离不满足骑行者横穿马路的需求,车辆进入紧急制动状态,应以最大制动压力150 Pa制动避障,即仿真结果符合避障算法设计。
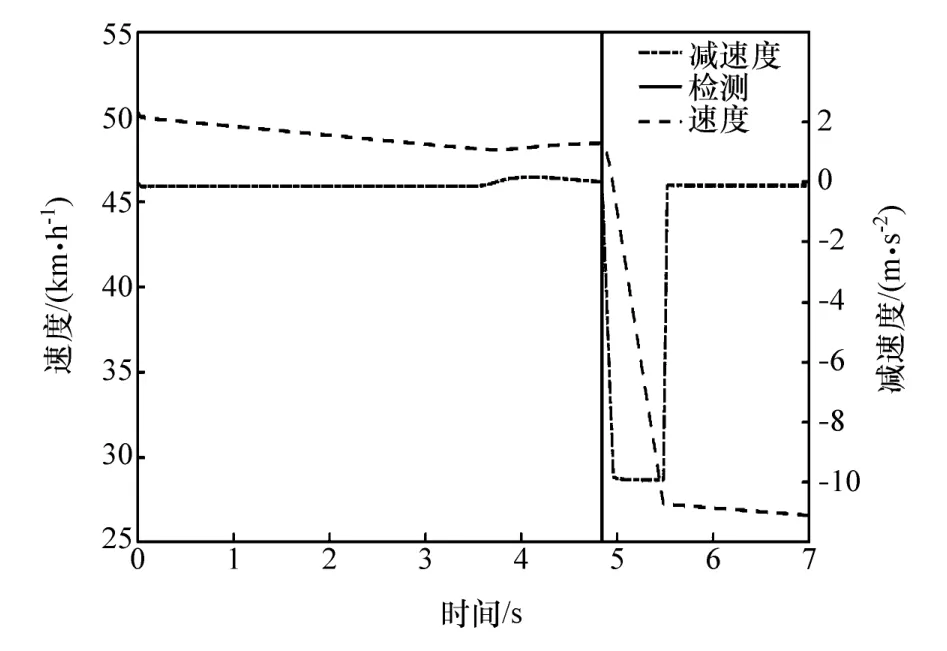
图10 主动避障算法控制下自车的速度、减速度曲线
在该仿真场景中加入基于时距的PreScan示例避障算法,运行仿真。图13显示了避障过程中自车速度、减速度变化趋势,图14为示例避障算法控制下自车的制动压力曲线。由图可见,在t=4.84 s时车辆以最大制动压力150 Pa制动,避免与骑行者碰撞。
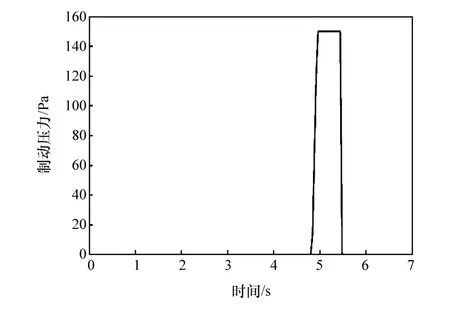
图11 主动避障算法控制下自车的制动压力曲线
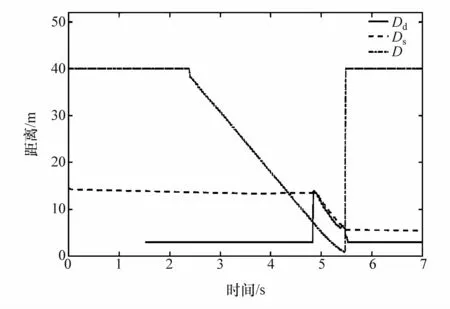
图12 间隔距离D、阈值D s和D d关系曲线
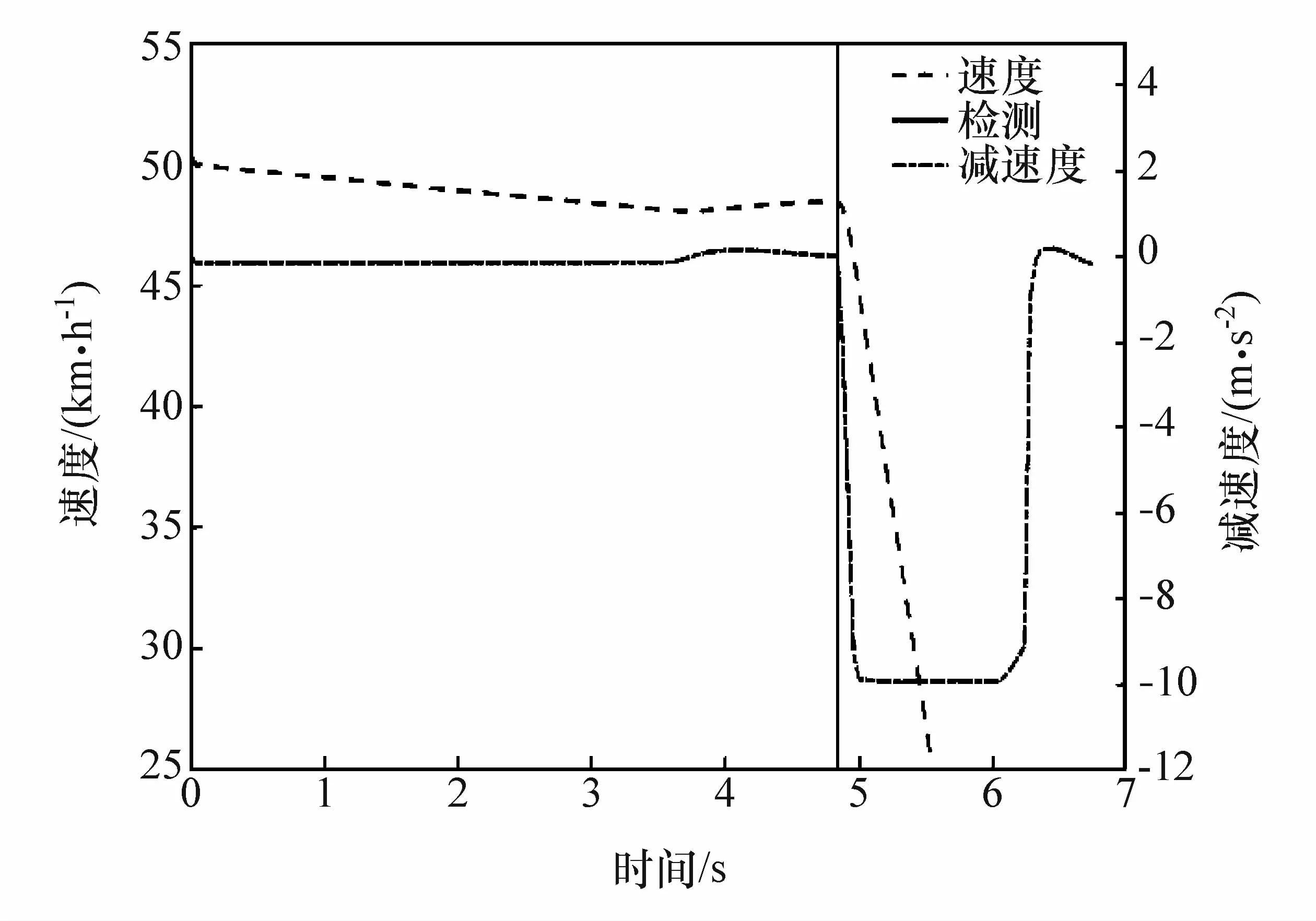
图13 示例避障算法控制下自车的速度、减速度曲线
由仿真结果可知,在主动避障算法或基于时距的PreScan示例算法控制下,车辆都可避免与骑行者碰撞,且本文提出的基于横向安全距离的主动避障系统,可达到与示例算法相同的制动效果,并在检测到骑行者通过后可主动控制制动返回,完成避障系统的主动控制。
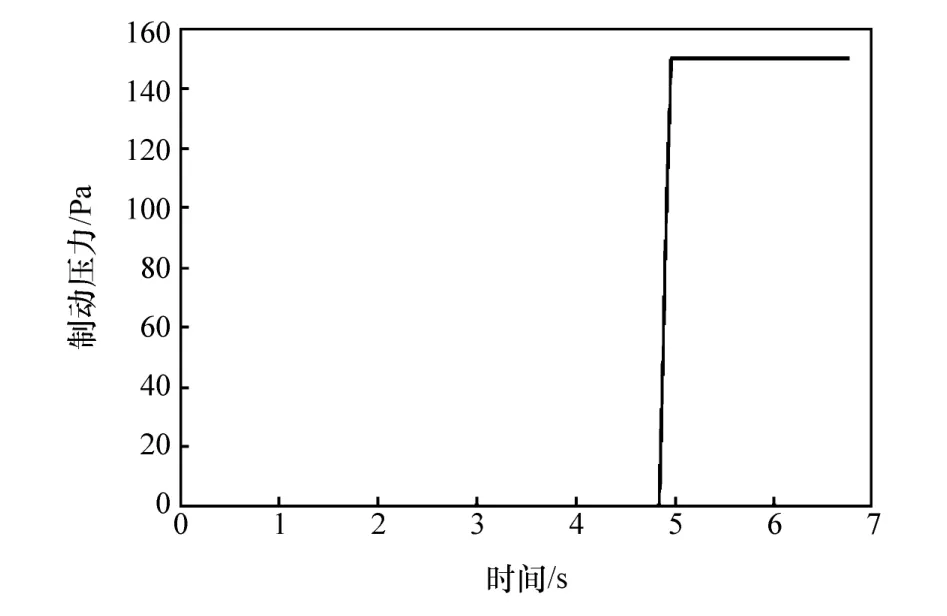
图14 示例避障算法控制下自车的制动压力曲线
5 结论
本文中利用移动目标横穿马路的速度、相对位置,建立横向安全距离模型,并提出一种基于横向安全距离模型的主动避障算法。同时,对移动目标进行停留检测,修正移动目标随机移动特性对避障控制的不确定性影响;引入路面附着系数,减小道路条件对汽车制动性能的影响。
以典型横向移动目标— 骑行者作为研究对象,利用PreScan/Simulink/Carsim联合仿真验证避障算法的有效性。仿真结果表明:本文中提出的基于横向安全距离模型的主动避障算法能有效避免与骑行者碰撞,并在检测到骑行者通过后可主动控制制动返回,完成避障系统的主动控制,提高行车的主动安全性。
