不同雷诺数下车辆队列尾车发动机舱盖气动特性研究*
2020-05-28戴文童李启良李卓明常艺菲杨志刚
戴文童,李启良,李卓明,常艺菲,杨志刚
(1.同济大学,上海地面交通工具风洞中心,上海 201804; 2.博格华纳(中国)投资有限公司,上海 200241;3.上海市地面交通工具空气动力与热环境模拟重点实验室,上海 201804)
前言
随着智能车和车联网技术的发展,高速行驶下的近距离跟车行驶将成为可能[1],因此有必要对不同车辆队列结构和存在相对运动下的空气动力学问题进行研究,以明确车辆队列运行与单车行驶的差异。
国内研究人员对超车的空气动力学问题进行过一些研究。傅立敏等[2]使用有限递增法将动态过程离散,模拟了两辆Ahmed body的超车工况,探究了纵向相对距离对两车气动特性的影响。研究发现,超车车辆从被超车后一倍车长到超过被超车一倍车长的过程中,被超车的阻力系数、侧向力系数和横摆力矩系数曲线均呈谐波形状;作用在汽车上的侧向力和横摆力矩都对汽车的横向稳定性有着重要的影响。胡兴军等[3]使用分区动网格构建动态计算域,结合雷诺应力模型模拟了两辆Ahmed body在横向间距为0.25、0.50和1.00倍车宽下的超车行驶工况下的流动特性发现,在同样超车条件下,被超车的气动力系数比超车车辆变化剧烈,变化幅度更大;在不同的横向间距工况下,横向间距越小车辆间气动干扰越大,气动力系数变化越剧烈,变化幅度也越大。为了探究相对车速对非定常流场的影响,吴允柱等[4]采用动网格技术实现了两辆Ahmed body超车过程中外流场的三维非定常模拟。研究结果表明,相对车速对主超车的影响较小,对被超车的影响较大;被超车的侧向力系数和横摆力矩系数随两车相对车速增加呈线性增加的趋势;在相同的相对速度下,绝对速度较低的两辆车在超车过程中产生的非定常气动影响更大。国外研究者同样关注车辆队列的气动特性,文献[5]和文献[6]中采用缩比模型风洞试验研究发现,车辆队列中单车的气动阻力与车辆的相对位置、跟车数量、前车的尾部结构等因素有关。通过对Ahmed body、长方体等简化模型车辆队列中的流动进行数值模拟发现,随着车辆间距增大,前车尾流的发展更加充分,涡量增大[7-8]。
车辆队列行驶在减阻的同时也产生了新的空气动力学问题,当两辆或多辆汽车以较小的间距高速行驶时,各车流场相互间的干扰非常强烈,使流场表现出明显的非定常特性。气流的非定常脉动能激发车身板件的振动并辐射噪声,影响汽车的振动与噪声性能。汽车发动机舱盖由于直接与前车非定常尾流相作用,容易产生振动与变形[9-10]。
以往研究表明,与单车运行相比,车辆队列运行对应流场更加复杂,气动力等气动特性因素产生了显著变化。为加深理解车辆队列运动的流场,明确两车间的流动特性,探明车辆队列运行的雷诺数效应,本文中选取车辆队列中典型工况,模型风洞试验与数值仿真相结合,分别研究缩比模型和实车模型车辆队列气动特性,重点关注雷诺数不同导致车辆队列间流场结构和尾车发动机舱盖气动特性的差异。
1 数值仿真方法
1.1 缩比模型
基于上海地面交通风洞中心气动 声学风洞真实结构尺寸,建立1∶15缩比模型。为了减少网格数、节省计算资源,截取全回路风洞中的部分作为缩比汽车模型仿真边界。整个计算域包含收缩段、喷口、试验段、收集口和扩散段,如图1所示。试验段的长、宽和高分别为1.517、1.185和0.818 m,喷口宽度和高度分别为0.433和0.283 m,喷口距收集口0.99 m。仿真汽车模型为两厢轿车,其比例为1∶18以满足两个模型在试验段中的布置和较小阻塞比的要求。

图1 缩比模型计算域示意图
分别采用HYPERMESH和STARCCM+完成计算域内面网格和体网格划分。所有表面划分成三角形面网格。位于后视镜表面的面网格最小尺寸为0.2 mm。发动机舱盖表面网格大小为0.5 mm,其他车身表面的网格尺寸大约为0.7~1.5 mm。外边界的面网格尺寸较大。收缩段面网格尺寸为15 mm,试验段地面和四周网格分别为8和20 mm,扩散段为15 mm。面网格总数约为180万个。为更好地求解近壁面非定常流动,在生成边界层网格时取无量纲壁面距离y+为1,增长率为1.2,共计生成12层,总厚度为1 mm。对于重点关注的前、后车附近流动区域,特别是前车尾流区域,进行网格加密,以期更精确地求解其流场。采用 TRIMMER和PRISM LAYER的体网格生成方式共计生成2 500万个体网格,图2为Y=0截面的网格分布示意图。

图2 Y=0截面网格分布
采用Realizable k-ε湍流模型对计算域进行定常流动求解。收缩段入口设置为速度入口,设定数值可以满足喷口出口风速为30 m/s。以模型车长作为参考长度,该风速对应雷诺数为4.9×105。扩散段出口设置为自由出口。使用基于不可压缩的求解器与隐式SIMPLE压力和速度耦合算法进行求解。迭代5 000步能满足收敛。采用WALE亚格子模型的大涡模拟进行非定常流动求解。以定常流动结果作为非定常流动计算的初始条件。以0.5 ms的时间步长,迭代2 000个时间步即能使流动进入动态变化阶段,然后继续以0.5 ms为时间步长进行采样,共采集了3 s的流动数据,即6 000个时间步。
1.2 实车模型
将实车模型放置在无限大空间的计算域中,如图3所示。计算域长为11倍车长L,宽为7倍车宽W,高为6倍车高H。前车头部距入口边界的长度为3L。
模型面网格尺寸最小位于后视镜表面,最大位于长方体计算域的上边界和左右边界,尺寸分别为3和160 mm。发动机舱盖表面面网格尺寸为8 mm,其他车身表面面网格尺寸约为10~15 mm。为了避免地面区域网格长细比过大,将地面设置为移动地面从而避免在地面生成边界层网格。车身表面创建总厚度为1.75 mm的边界层网格,边界层网格增长率为1.2,共生成8层。前后车附近区域进行网格加密,整个计算域创建约2 800万的体网格。

图3 实车模型计算域
采用与缩比模型相同的湍流模型进行定常和非定常流动仿真。上边界和左右边界设置为对称边界。入口设置为速度入口,给定入口速度为30 m/s。以实车模型车长作为参考长度,该风速对应雷诺数为8.8×106。出口设置为压力出口,给定压力为0。
2 仿真与试验对比
由于无法在全尺寸风洞内进行车辆队列行驶的气动试验,为验证本文数值计算方法的正确性,在结构相同的1∶15缩比模型风洞进行试验。使用压力传感器测量车辆队列尾车表面6个测点的表面静压,使用表面传声器测量发动机舱盖测点的表面压力脉动,测点分布如图4所示。P1~P6分别对应发动机舱盖、前风窗、前侧窗、后侧窗、车顶和尾窗,F1测点为发动机舱盖压力脉动测点,其位置与P1点关于Y=0平面对称。

图4 模型风洞及测点布置
根据所测得的发动机舱盖表面静压,计算表面静压系数,其定义为

式中:Cpi和pi分别为表面静压系数和表面静压;pref和p0d分别为参考点的静压和动压。风洞试验段压力平衡口的中心位置被设置为压力参考点,因其与外界大气相通,参考压力为0。喷口出口处的动压p0d=ρv2/2。ρ和 v分别为流体的密度和喷口出口流速。
图5(a)为喷口风速为 30 m/s、两车间距 0.3L时试验与仿真的6个测点压力系数对比。由图可见,数值仿真结果与试验结果趋势基本相同,数值相差不大。图5(b)为0.3L纵向间距下,前车侧向偏移0.6W工况中试验与仿真测点压力系数对比。与前一工况相比,仿真结果比试验结果略微偏小,但两者曲线的总体走向趋势基本相同。

图5 试验与仿真测点压力系数对比
图6 给出了发动机舱盖测点试验和仿真的压力脉动频谱图。由图可见,非定常仿真能捕捉到约76 Hz的主峰,频谱变化趋势与试验吻合。通过图5和图6的数值仿真与试验结果对比可确认本文采用的数值仿真方法是有效的。

图6 纵向间距0.3L,试验和仿真发动机舱盖测点压力脉动频谱
3 车辆队列定常气动特性对比
3.1 纵向相对位置
实车模型和缩比模型尾车发动机舱盖的表面静压分别用入口速度和喷口风速进行归一化处理以得到静压系数云图,如图7所示。在发动机舱盖主要区域缩比模型的静压系数要略微高于实车模型。实车模型发动机舱盖前端陡直区边缘处呈现为明显的高压区,而缩比模型的前端陡直区域的静压系数与后部主要区域相比变化不大。这表明与缩比模型相比,从发动机舱盖后端到前端,实车模型表面静压梯度更大。
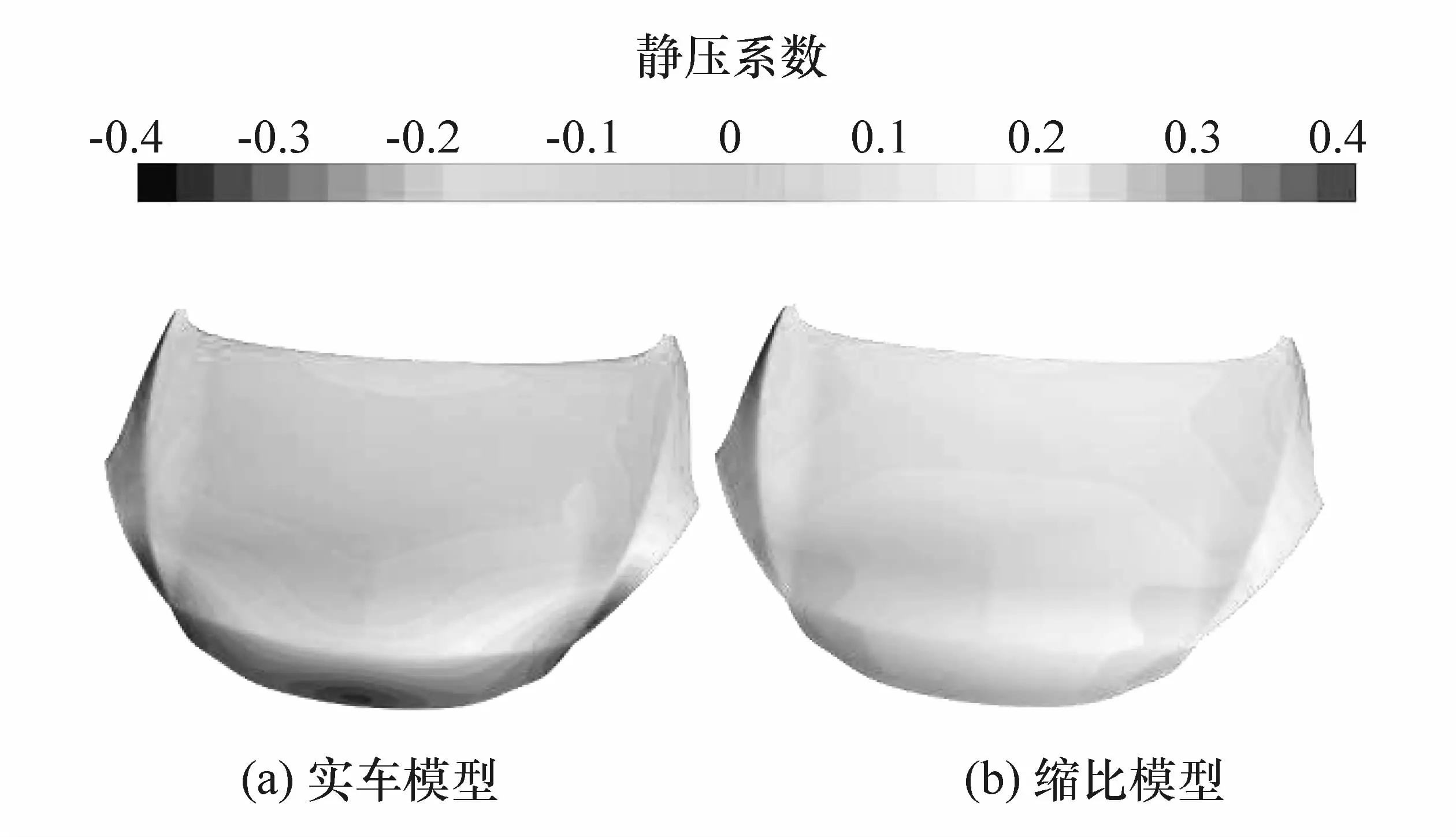
图7 尾车发动机舱盖表面静压系数
发动机舱盖表面静压和其附近的速度场紧密相关。图8为两种模型Y=0平面的速度场云图。由图可见,缩比模型前车尾部有一个明显的涡旋区域。从尾部上端扰流板延长线到发动机舱盖前端和从底部延长线到尾车进气端表现为两条明显的低速轨迹。在实车模型中,沿前车尾部上端扰流板依然有一条向下后方延伸的低速尾迹,但该尾迹尚未延伸到发动机舱盖前端便开始加速;前车尾部底部的低速尾迹并未沿来流方向延伸而是向上偏离且较短。对比两种模型,可发现在前车尾部下端,实车模型的速度要明显高于缩比模型;而在发动机舱盖主要平面附近的区域内,两种模型的速度分布比较相近。
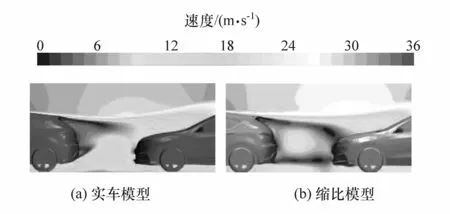
图8 Y=0平面速度云图
图9 为两种模型中Z=0.45H(H为模型车高,该高度对应平面与发动机舱盖前端陡直处边沿平齐)平面速度云图。由于雷诺数的差异,前后车之间的间隔区域呈现出完全不同的流动结构。从形状上来看,实车模型前车尾部两侧对称的片状低速区可视为用平面截断两侧尾涡所得;而中间速度较高的区域表示从底部径直流向发动机舱盖上方的气流。从低速区的长短可以判断,缩比模型尾涡相对尺度的大小要大于实车模型。同时,从前车尾迹扩散程度来看,缩比模型尾迹明显扩散得更开,而实车模型的上下两条尾迹线几乎平行。这可推断出,缩比模型的两车间隔区域整体呈现出更高的静压,从而推动两侧的来流向两侧扩散。

图9 Z=0.45H平面速度云图
3.2 横向相对位置
图10 为纵向间距0.3L、前车侧向偏移0.6W时发动机舱盖表面静压系数云图。图中两种模型静压在空间的分布非常接近。发动机舱盖前端陡直区为明显正高压区,后部主要表面为负压区,其中在左侧棱角区域更加明显。图11为两种模型Y=0平面的速度云图。由图可见,发动机舱盖前端陡直区与驻点位置接近,速度接近0,静压较高。对比两种模型的速度场可以发现,在两车间隔区域的底面附近,缩比模型的速度更低,沿Z轴方向的速度梯度更大。

图10 前车偏移0.6W时发动机舱盖表面静压系数

图11 Y=0平面速度云图
图12 为Z=0.45H平面的速度场云图,两种模型最大的不同在于前车的尾迹区。实车模型由于后车对气流的阻挡作用,在前车尾部后车近端形成了一片低速的死水区,而该区域随着远离后车的方向越来越小。而缩比模型这一低速区域在前车尾部后车远端依然很明显,这表明缩比模型前车尾迹区的速度要低于实车模型。同时,从尾迹区边界的形状来看,实车模型呈现出先收缩再缓慢扩散的趋势,而缩比模型则是始终呈现明显的扩散趋势。

图12 Z=0.45H平面速度云图
4 车辆队列非定常气动特性对比
4.1 纵向相对位置
图13为尾车发动机舱盖表面压力脉动均方根值云图。由图可见,两种模型的最强脉动均发生在发动机舱盖前端陡直边沿的两侧,并沿着发动机舱盖由前向后逐渐降低。此边沿处处受到两侧脱落涡的直接碰撞且伴随着流动分离。从该区域的脉动等值线来看,缩比模型的脉动等值线更加平滑,而实车模型的脉动等值线变化更加无规律。这是因为在不同雷诺数下,尾部涡的相对尺度不同导致的。在发动机舱盖后部平滑区域,缩比模型的脉动强度要高于实车模型,这可能是因为缩比模型中涡的相对尺度更大。同时,在实车模型中,由于前车底部流出的气流速度更大,尾涡区较短,尾迹上扬导致气流带着涡旋向发动机舱盖上方直接流过而没有发生碰撞。故发动机舱盖主要平滑区域脉动强度较低。
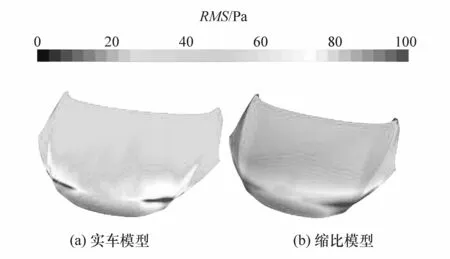
图13 尾车发动机舱盖表面压力脉动均方根值云图
发动机舱盖表面的压力脉动源于流场的压力脉动。图14为两种模型某一时刻Y=0平面(左图)和Z=0.45H平面(右图)非定常脉动压力云图。图中脉动压力数值是通过某一时刻非定常的压力减去平均压力而得到。图中可明显看到前车尾部上端扰流板和底部发生涡脱落现象,形成相邻两涡之间脉动方向始终相反。在实车模型中,可以发现上部扰流板处脱落的涡尺度增长非常迅速,且在离尾部很近的地方便开始破裂;下部脱落的涡受到压力梯度的影响呈斜向上移动的趋势,并与上部涡的运动相互干扰,在两车间隔的中间区域的脉动呈现出一种很混沌的状态。而在缩比模型中,可以发现其尾涡的相对尺度要明显高于实车模型,且在两车间隔区域,两侧涡的干扰并不特别剧烈。两车间隔区域涡的运动并非简单的移动,而是一个由涡破裂、涡配对和涡融合构成的复杂过程。刚刚脱落形成的涡除向前移动外,还受到压力梯度的影响立即破裂成较小的涡,之后又与附近的小涡配对融合成较大的涡。在不断变化和移动的过程中,一些涡撞击到发动机舱盖表面,造成了瞬间的压力脉动增长。
4.2 横向相对位置
前车侧向偏移0.6W时发动机舱盖表面压力均方根云图如图15所示。脉动较强的位置集中在右侧和远端靠近雨刮槽的位置。左侧大部分表面为低脉动区。发动机舱盖右侧的脉动来源于前车尾部后车近端一侧的尾涡,而雨刮槽位置处的脉动来源于该处本身的流动分离。对比两种模型的脉动云图可见,两者脉动强弱区域的分布基本相同,但实车模型在左侧的脉动强度更低一些,且在某位置脉动能量的分布比较混乱。这可能与网格相对精度和较高雷诺数下涡的相对尺度与运动状态不同有关。

图15 尾车发动机舱盖表面脉动压力均方根值云图
图16 为该工况下 Y=0平面(左图)和 Z=0.45H平面(右图)上的脉动压力场。由图可见,当前车侧向偏移0.6W时,尾车Y=0平面(左图)与前车不会相交,故此平面上尾车所面对的来流与自由来流相似,脉动压力较低。发动机舱盖表面除了后端与雨刮槽连接的拐角处因为大分离而产生的局部表面压力脉动,其他区域的脉动强度较低。从Z=0.45H平面(右图)看,前车尾部后车近端一侧脱落的涡能作用到尾车发动机舱盖的一侧区域,由于缩比模型中前车尾涡的相对尺度更大,能作用到发动机舱盖更大的相对面积。对比两种模型,可以发现在实车模型中后车近端一侧的前车尾涡有整体向远端一侧收缩的趋势,而缩比模型则不明显。这是因为实车模型中,两车间隔的绝对尺度要远大于缩比模型。在两种模型来流速度几乎相同的情况下,两车间隔的绝对尺度越大,流线弯曲所需的压力梯度就越小,故气流更多地从前后两车中间绕过,其流动轨迹也影响了涡的运动。

图16 前车偏移0.6W时脉动压力场对比
5 结论
对典型纵向和横向相对位置的车辆队列运动进行了定常和非定常的数值仿真,得到了这些工况下发动机舱盖表面压力的定常和非定常气动特性。同时对计算域的Y轴和Z轴截面的平均速度场、脉动压力场进行了对比,得到了在不同雷诺数下尾车发动机舱盖与流场所表现的不同特征,结论如下。
(1)使用从喷口入口到收集口出口的计算域,采用Realizable k-ε湍流模型可以得到较准确的发动机舱盖表面的定常静压,使用大涡模拟能够比较准确地捕捉到发动机舱盖表面的脉动压力。
(2)对于典型相对位置工况,实车模型与缩比模型在前车尾迹区的流动特征有一定区别。在定常条件下,两种模型发动机舱盖表面静压分布基本相同。在Y轴截面上,实车模型的前车尾迹比缩比模型更加上扬,底部区域速度更快;在Z轴截面上,缩比模型的尾涡相对尺度更大,且几何上尾迹区扩散程度更高。而在非定常条件下,实车模型由于前车尾涡相对尺度较小,扩散得更充分,尾迹区涡的分布状态更加混沌,发动机舱盖表面脉动能量的分布更加混乱。
(3)当前车无偏移时,受到尾涡撞击的作用,尾车发动机舱盖脉动能量集中在前端陡直处。当前车偏移一定量时,受到一侧尾涡作用的部分发动机舱盖表面压力脉动依然剧烈。已经暴露在自由来流中、脉动能量最高的位置是后端与雨刮槽连接处的拐角,该处存在明显的流动分离,且在Y轴平面内产生一对旋向相反沿风窗玻璃向上运动的涡。
(4)涡在两车间隔区域的运动并非简单的移动,而是一个由涡破裂、涡配对和涡融合构成的复杂过程。刚刚脱落形成的涡除向前移动外,还受到压力梯度的影响而破裂成较小的涡,之后又与附近的小涡配对融合成较大的涡。在不断变化和移动的过程中,一些涡撞击到发动机舱盖表面,造成了压力脉动的增大。
