模糊测度的零连续性
2020-05-27谭浔晓张承坤徐鹤萍李军
谭浔晓,张承坤,徐鹤萍,李军
(中国传媒大学数据科学与智能媒体学院,北京 100024)
1 引言
1954 年,法国数学家G.Choquet提出了容度(capacity)的概念,定义了一种基于容度的非线性积分,现称为Choquet积分[4]。1974年日本学者Sugeno提出了模糊测度和模糊积分的概念[16],用于模糊数学中的模糊评判。所谓Choquet容度或模糊测度是通过公理定义在某个集合系统上的一类特殊的集合函数,不要求可加性。因此,它是概率测度的推广,在不同领域分别被称为容度、模糊测度、非可加测度、单调测度和非可加概率等,见文献[4],[5],[12],[14],[16]和[17](本文中我们将统称为模糊测度)。上世纪七十年代以来,模糊测度的研究日益受到人们的重视。特别是近二十多年,人们在模糊测度和相应的非线性积分研究领域取得了丰富成果(见文献[5],[6],[7],[10],[15]和[17])。
由于模糊测度失去了经典测度(或概率)理论中赖以生存的可加性,因此,经典测度理论中的许多结果在模糊测度理论中已不再成立。为了将经典测度理论中的结果推广到模糊测度情形,需要对模糊测度附加一些新的结构,即讨论具有一些特殊结构特性的模糊测度,如:次可加性、超可加性、上(下)连续性、序连续性、零可加、弱零可加、上(下)自连续性和正则性等。在一定的条件下,经典测度的许多重要结果在模糊测度空间上得到了有效的推广(见文献[5],[6],[7],[10],[15],[17],[20])。
基于模糊测度的非线性积分,如Choquet积分[4],Sugeno积分[16],Shilkret积分[15],泛积分(参见文献[19],Sugeno积分和Shilkret积分是它的特例)以及近几年引入的凹积分[7]是几类重要的非线性积分。对这些积分的研究人们也取得了丰硕的成果。经典勒贝格积分的基本性质和许多重要定理也被推广到了非线性积分理论中(见文献[6],[7],[14],[17])。

本文中,我们将进一步讨论模糊测度的零连续性,它是与上(下)连续性、序连续性和上(下)自连续性不同的结构特性。我们给出一些例子说明模糊测度的零连续性与其它几个常见的结构特性,如:上(下)连续性、序连续性、零可加性和弱零可加性之间的关系。我们将看到模糊测度的零连续性是比下连续性更弱的一个条件。我们将要证明:如果模糊测度是零连续的,那么上述的积分的唯一性对于一般的泛积分(从而对于Sugeno积分和Shilkret积分)和Choquet积分也是成立的。因此,先前得到的相关结果得到了进一步推广。最后,我们利用可测函数的收敛性刻画模糊测度的零连续性,给出零连续性的几个等价条件。
2 预备知识


f=0a.e.于A(当X=A时,简记为f=0a.e.);如果μ({x∈X:f=+∞}∩A)=0,则称f在A上几乎处处有限,记作f<∞a.e.于A(当X=A时,简记为f<∞a.e.)。

(1)若μ(φ)=0且μ(X)>0;



在许多文献中,模糊测度也被称为容度、单调测度、非可加测度或非可加概率。
我们陈述以下一些概念(参见文献[5][9][14][17]).
模糊测度μ称为


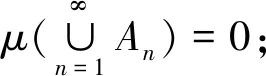






当⊕=+,即泛加法等于通常的算术加法时,上述“次泛可加”、“泛可加”和“σ-泛可加”分别退化为经典测度论中的次可加、有限可加和σ-可加概念。
明显地,单调测度的零可加性和可数弱零可加性均蕴含着弱零可加性;σ-泛可加性蕴含着泛可加性和可数弱零可加性。
性质2.1如果μ是次泛可加的,那么μ是零可加的,从而μ也是弱零可加的。

μ(A∪B)≤μ(A)⊕μ(B)
=μ(A)⊕0
=μ(A).
另一方面,由μ的单调性μ(A∪B)≥μ(A),故
μ(A∪B)=μ(A).
因此μ是零可加的。
性质证毕。
性质2.2如果μ是σ-泛可加的,那么μ是下连续的。
证明:与经典测度相应结论的证明类似。
3 模糊测度的零连续性
下面我们回顾模糊测度的零连续的概念(参见文献[1])。

以下例子说明不是每个单调测度都是零连续的。


明显地,我们有以下性质
性质3.1如果模糊测度μ是下连续的,那么μ是零连续的。
然而性质3.1的逆命题不一定为真。以下例子说明单调测度的零连续条件确比下连续条件弱。
例3.2设X=(自然数集),=(X),令定义μ:→[0,1]如下:

的当且仅当μ同时是零连续和弱零可加的。
由性质2.2可得:
性质3.2如果模糊测度μ是零连续的,那么模糊测度μ就是弱零可加的。
性质3.3如果μ是σ-泛可加的,那么μ是零连续的。从而μ的σ-泛可加性蕴含着μ的零连续性。
性质3.4[1]如果μ是弱零可加和强序连续的,那么μ是零连续的。
性质3.5如果μ是零可加和序连续的,那么μ是零连续的。
注1.以下例子说明强序连续性和弱零可加性没有必然的蕴含关系。
例3.3设X=(自然数集),=(X),令定义集函数μ:→[0,1]如下:


不难看出,上述例3.3中的单调测度μ是零连续的(从而,由性质3.2可知μ是可数弱零可加的)。注意μ不是强序连续的;同时注意到例3.1中的单调测度μ不是零连续的,但不难验证它是强序连续的。即说明零连续性和强序连续性没有必然的蕴含关系。
注2.零连续性与弱零可加性没有必然的蕴含关系。
例3.4设X=(自然数集),=(X),定义定义单调测度μ:→[0,1],如下:
其中符号|A|表示集合A中元素的个数。容易看出μ是弱零可加的。不难验证,单调测度μ不是零连续的。


那么μ是零连续的。但μ不是弱零可加的(从而也不是零可加的)。
注3.零连续性与零可加性也没有必然的蕴含关系。
下面我们回顾最优测度的概念(参见文献[7]).


μ(A∪B)≥μ(A)⊕μ(B).

性质3.7μ是零连续的当且仅当μ⊕是零连续的。
4 泛积分的唯一性
下面我们回顾非负可测函数的泛积分的定义.

和Shilkret积分[15]:
泛积分有以下基本性质(可参见文献[11][13][17][18]).



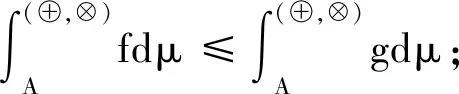
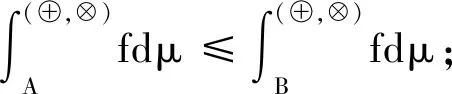



证明:(1)参见文献[17]。
(2)令
An=μ({f>1/n}∩A)=0,n=1,2,3,…,
那么
由性质4.1,对每一个n=1,2,…,可得
即
由泛乘法的公理性质(参见文献[17])可得μ(An)=0,n=1,2,3,…。因为μ是零连续的,所以μ({f>0}∩A)=0,即f在A上几乎处处为零。
定理证毕。
作为定理4.1的特例,我们即可得到文献[13][16]中的结果:
推论4.2[17]若μ是下连续的,则

定理4.1表明在模糊测度是零连续的假定下,

5 Choquet积分的唯一性
Choquet积分是一类重要的非线性积分,它的定义如下(见文献[4][14][17]):

其中右边的积分是关于α的黎曼积分,α∈[0,∞)。
Choquet积分有以下基本性质(可参见文献[15][17]).




对于Choquet积分也有与泛积分类似的结果。


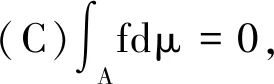
证明:(1)见文献[15][17]。
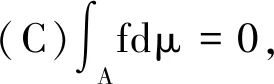
由假设μ是零连续的,从而μ({x:f(x)>0}∩A=0。即得f=0 a.e.于A.
定理证毕。
作为定理5.1的特例,我们即可得到文献[17]中的结果:

由定理4.1和5.1可得以下结果:

(1)f在A上几乎处处等于零,即f=0 a.e.于A;

最后我们利用可测函数的收敛性刻画单调测度的零连续性,给出零连续性的几个等价条件。
定理5.2设(X,A,μ)是一个单调测度空间,以下几个条件等价:
(1)μ是零连续的;




证明:我们仅证(1)⟺(2),其余可类似证明。

(2)⟹(1):任取{An}⊂A,An↗A,且μ(An)=0,n=1,2,...。令fn=XAn,f=XA(XAn,XA分别表示An和A的特征函数),那么fn=0 a.e.且fn↗f,由条件(2)有f=0 a.e.,即XA=0 a.e.,亦即μ(A)=0。
证毕。
6 结论
本论文中,我们讨论了模糊测度的零连续性,正象我们已经看到的,模糊测度的零连续性是比下连续性更弱的一个条件。在零连续的条件下我们证明了勒贝格积分的唯一性对于一般的泛积分和Choquet积分仍然成立(定理4.1和5.1)。这样,作为泛积分特例的Sugeno积分和Shilkret积分也有相同的结果。因此,人们先前得到的相关结果(参见文献[17])得到了进一步推广。最后,我们揭示了模糊测度的零连续性和可测函数的收敛性之间有紧密联系(定理5.2)。
再进一步的研究中,我们将问题的讨论集中到凹积分[7]的情形,考察凹积分的相关性质。
