基于特征模型融合的相关滤波跟踪算法
2020-05-27吴雨秋李朝晖
吴雨秋,李朝晖
(中国传媒大学信息与工程学院,北京 100024)
1 引言
计算机视觉中的一项很重要的内容是视觉目标跟踪,同时它也是交互式视频的前提。视觉目标跟踪技术融合了图像处理、模式识别、人工智能、自动控制等多个领域的技术,也是进行智能机器人研究的重要技术之一,因此目标跟踪算法的研究具有重要的理论意义和实际价值。基于相关滤波跟踪算法以其大大提升跟踪能力和良好的实时性等两大优势成为目前最主流的基础框架,也是近年来实际应用最广泛的跟踪算法。并且,此算法还有很大的发展前景。目前,有很多研究者还在通过不断优化和改进基于相关滤波的跟踪算法框架的各个部分来提升其跟踪的性能。
对视频序列里感兴趣的目标区域相关滤波器会产生相应的峰值,而对目标背景的影响值会比较低。所以,相关滤波器可以被作为检测器来使用。2010年Bolme[1]利用相关滤波器原理提出了误差最小平方和滤波器(MOSSE),同时为了更好地实现目标跟踪,创造了一种自适应的训练方法。这种方法充分展示了相关滤波器在视觉跟踪中的突出表现。2014年Henriques[2]等在机器学习岭回归框架下学习滤波器,利用循环矩阵和快速傅里叶变换(FFT)加速,并将核技巧(kelnel trick)融入学习框架,将多通道的 HOG 特征替代单通道的灰度特征,提高了滤波器的判别能力,提出一种核相关滤波跟踪器(KCF),不加入核技巧的为DCF,之后很多学者提出的算法都是基于KCF/DCF的。
Li等提出尺度自适应多特征跟踪器(SAMF)[3],采用灰度特征、CN 特征和 HOG 特征串联,提升了跟踪器的整体性能。Bertinetto等人提出了利用HOG特征和全局颜色直方图特征的Staple[4]算法,此算法利用了两种互补的特征。HOG特征通过相关滤波器产生响应图,通过颜色直方图产生直方图概率模型,之后融合两种模型的响应图,估计目标位置的变化。两者结合能够很好的解决目标发生形状改变和光照的改变的问题。Ma C等利用CNN模型前、后项卷积层的特点提出了CF2[5]算法,算法利用后向卷积特征应对目标的外形问题,可以减少模型偏移的发生;同时采用前向卷积层中的特征来对模板进行准确定位。此算法将提取卷积神经网络(CNN)特征应用到跟踪器中,采用多层相关滤波响应图共同来确定目标位置,使得跟踪结果更加准确。Danelljan M提出了综合SRDCF[21]深度算法和SRDCFdecon[22]深度算法的C-COT[6]算法,将DeepSRDCF中的单层特征变为多层特征,进行连续的空间域插值,生成多分辨率的特征图变得更加容易,对目标的定位也更加精准。
综上所述,图像特征的选择对跟踪效果有很大影响。虽然基于相关滤波目标跟踪的研究已经取得了显著的成果并且得到了广泛的应用,对于实际应用来说,仍然面临许多复杂问题,例如目标外观发生形状变化、快速运动及跟踪出现偏移等,这些问题会对跟踪性能产生严重影响。本文针对相关滤波目标跟踪中目标形变和快速运动的问题提出解决方案。
2 基于相关滤波的目标跟踪基本算法
基于相关滤波的目标跟踪一般框架[10]如图1所示,包括:1)根据序列第1帧标定的目标位置提取一个图像块,将它进行训练以初始化相关滤波器。2)对于当前帧,根据前一帧的目标位置提取候选图像块的特征,用余弦窗平滑边缘信息。3)将处理后的特征进行离散傅里叶变换(FFT)来与相关滤波器相乘。4)通过傅里叶逆变换(IFFT)得到响应图,响应图中最大值所对应的坐标位置即被认为是目标的新位置。5)根据新的目标框进行特征提取,更新相关滤波器。

图1 相关滤波算法基本框架[10]
下面将对相关滤波算法作详细说明。
目前跟踪算法主流的思想是基于检测的跟踪,对输入的图像序列进行样本采集,以目标位置为基础,离目标近的被标记为正样本,远离目标的标记为负样本。大部分算法给正样本的标签设置为1,负样本设置为0,以此完成训练样本的标记。这种方法对离目标位置远的负样本和离目标位置近的负样本一样看待,没有考虑每个负样本权重的问题。而相关滤波器算法则采用岭回归的方法,使样本标签为[0,1]范围的不同数值,从而不同距离的样本得到不同的权重。也就是样本离目标越近,其权重越接近1,离目标越远,权重值越趋向于0。
根据机器学习理论可知,判别式模型的样本训练过程就是一个最小化损失函数的过程,即使分类函数f(x)=WTx依据一定的方法使损失最小。W是分类器系数,如果损失函数使用均方误差,则这个过程可以如下表示:
(1)
式中,x为训练样本特征,y为其样本的标签,i为样本号,λ为规则因子。对其求偏导,得到一般解:
W=(XHX+λI)XHy
(2)
式中,XH是X的厄米特转置,如果矩阵是实矩阵,则有XH=XT。其中,X是由基样本循环移位得到的循环矩阵,具有以下性质:
(3)
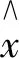
(4)
式中,⊙是矩阵的点乘,将其带入(2-6)式可得频域表达式:
(5)
核函数可以实现样本x从低维到高维φ(x)的非线性映射,所以系数可写成如下表达方式:
W=∑αiφ(xi)
(6)
这时候优化问题就从求W变成求α了,因此回归函数的表达方式是:
(7)
该式的解为:
α=(K+λI)-1y
(8)
式中,K是核循环矩阵,Kij=κ(xi,xj)。I是单位矩阵,向量y的元素是yi,κ是核函数。
则可在傅里叶域内快速求得:
(9)
完成了滤波器的训练之后,就可以用已训练好的模型对目标位置进行预估了。采集测试样本给滤波器,得到响应图,相关滤波器的响应输出如下:
(10)
训练和测试的样本都由基础样本循环移位得到,因此构建核矩阵KZ,并使用高斯核变成循环矩阵,接上式可得:
f(z)=α(KZ)Τ
(11)
式中,f(z)是测试样本z所有的循环移位得到的样本的输出响应。其频域表示为:
(12)
测试响应f(z)的最大值的位置,就被认为是预测的目标位置。式(9)用来对分类器做训练,式(12)用来实现目标检测,这两个式子是相关滤波算法的两个重要公式。

(13)
(14)
式中,t表示当前帧序号,η表示学习率。
3 基于特征模型融合的相关滤波跟踪算法
相关滤波类算法属于模板类方法,此类方法当目标发生形变时,容易出现跟踪失败的问题。并且相关滤波类算法也存在边界效应问题,当目标移动过快时容易跟踪失败。而颜色直方图特征能够解决目标变形的问题,并且对目标快速运动不敏感。针对上述问题,本文通过融合两种模型的特征响应图,即基于直方图的特征概率模型图和基于相关滤波模版的响应模型图,之后根据融合模型估计目标位置的变化,确定目标位置。
3.1 目标特征模型的建立
优良的特征是实现良好跟踪的基础,深度学习方法得出的深度特征比传统的手工特征(HOG、灰度、CN、Harris等)更加精确。而相关滤波的核心思想是将计算转化到频域,相比于传统方法,跟踪速度得到了大幅度的提升。为了结合两种方法的优点,人们开始将深度学习引入到相关滤波中。本文选取提取深度特征的相关滤波算法CF2作为基本框架,分别建立深度特征滤波模型和颜色直方图特征概率模型。
本文利用VGG[11]网络提取目标得到深度特征,由于低层特征有较高的分辨率能进行精准定位,高层特征含更多语义信息能进行范围定位,因此分别提取高低两层的卷积特征;同时提取颜色直方图,生成直方图概率模型;从而建立特征目标融合模型。
3.1.1 深度特征滤波模型
卷积神经网络相关算法是近年来计算机视觉领域的研究热点之一,大量科研人员投身其中并提出了一系列模型结构。VGG-Nets是由英国牛津大学著名研究组VGG提出,由于其良好的泛化能力,其在ImageNet[12]数据集上的与训练模型被广泛应用于诸多计算机视觉相关问题。
相比于传统特征,由深度神经网络提取出的卷积特征拥有较强的抗干扰性,在图像分类算法的比赛中获得了突破性的成果。由此大量基于CNN的跟踪器也相继被提出。顶层卷积层得到的是更抽象、更高层次的语义特征,可以更好地区分对象的类别,而且能够很好地应对目标发生形变和遮挡得问题,不过对同类对象的区分效果就比较差。较低层的卷积层得到的特征更详细,更适合用来对目标进行定位,但是对改变外观的对象鲁棒性差。如图2中所示,左图为VGG-Net的conv3层输出的特征,高亮区域表示目标位置的所在的区域范围,所以可以看到目标的轮廓还是比较清晰的,在conv5层,则得到的特征含有更多的语义信息。

图2 VGG-Net输出特征图[11]
本文采用CNN网络提取特征,CNN网络采用由英国牛津大学提出VGG-Net,使用在ImageNet上面已经训练好的模型VGG-19,该网络由16个卷积层和3个全连接层组成。此网络模型使用ImageNet数据集中的130万张图像进行训练,拥有更深的架构,能够提供更多级别的深度特征,图像分类方面的大部分先进成果都是基于此模型实现的。
由于多层卷积的计算,使深度特征的提取比较耗时,所以本文只提取VGG-19的conv3-4和conv5-4两层特征,之后将这两个层特征分别经过相关滤波器得到不同的响应图,接着将两个滤波响应图进行加权融合,得到融合之后的响应图即为根据相关滤波算法预测的目标位置。
3.1.2 颜色直方图特征概率模型
由于相关滤波跟踪算法为了减少边缘的信息的干扰加了余弦窗来平滑边缘,使图像信息更接近于目标信息,但是当物体快速运动时,意味着在跟踪过程中下一帧目标的位置偏离搜索中心太远,在这种情况下给样本加余弦窗就会损失部分目标信息。这就是相关滤波算法的边界效应问题,此问题带来的影响就是当目标移动过快时容易出现跟踪失败。而且相关滤波算法也属于模板类方法,当目标发生形变也容易造成跟踪失败。
解决目标变形问题的方法是采用对形状变化不敏感的特征,解决快速运动问题的方法则是采用对运动变化不敏感的特征,而颜色直方图刚好能够解决快速运动和目标变形的这两个问题。相关滤波器是从循环移位学习的,而颜色直方图丢弃每个像素的位置,对于循环移位是不变的,所以可以利用颜色直方图解决此问题。
本文借鉴DAT[14]算法,统计前景目标和背景区域的颜色直方图并归一化,得到前景和背景的颜色概率模型,用贝叶斯方法判别每个像素属于前景的概率,得到像素级颜色概率图,再加上边缘相似颜色物体抑制就能得到颜色直方图特征概率模型了。
为了区分目标像素X∈O与目标周围的背景像素,在输入图像I上采用基于颜色直方图的贝叶斯分类器。令H)Ω(b)表示在区域Ω∈I上计算的非标准化直方图H的第b个bin中。另外,让bX表示分配给I(X)的颜色分量的bin。给定矩形目标区域O(即初始边界框注释或当前跟踪器假设)及其周围区域S,则就可以应用贝叶斯规则来获得位置x处目标的似然性:
(15)
3.2 特征模型融合跟踪算法整体流程
本文设计的跟踪算法的流程图,如图3所示,对于输入的一帧图像,首先提取一块搜索区域,搜索区域的大小为目标框的2.8倍。之后分为两个部分,一部分提取VGG-19的卷积3-4层和5-4层的特征,两层卷积特征分别经过相关滤波器得到两个滤波响应图,分别设为r3-4和r5-4。另一个部分对搜索区域进行前景和背景的颜色直方图统计,之后利用贝叶斯估计得到目标概率图,设为p。最后将两部分得到的响应图进行加权求和,就得到了融合图,设为s,融合图最大值的位置即为最终确定的目标位置。如果不是最后一帧,则进行相关滤波器和贝叶斯模型的更新,继续进行跟踪。
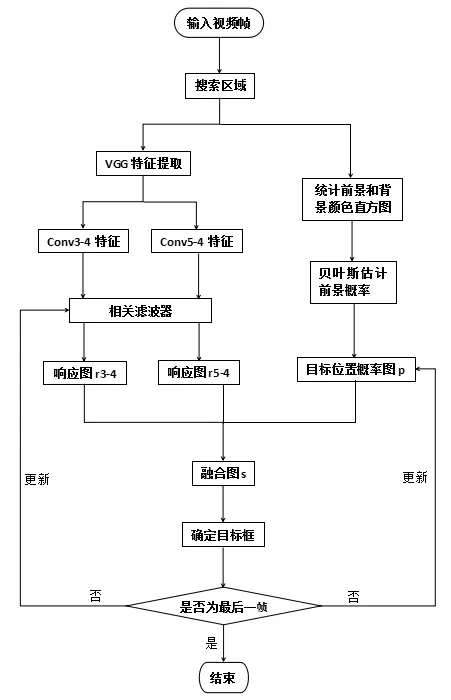
图3 算法整体流程图
在特征模型融合时,对两个响应图的权重进行了设置,由于深度神经网络提取的图像卷积特征的相关滤波模型能够更精确地确定目标位置,特征越深响应区域越小。对于跟踪任务来说,重点在于确定目标位置,所以r3-4和r5-4分别设置权重值为1和0.25,得到响应加权图r。而颜色直方图特征概率模型用来弥补相关滤波的目标形变问题,同时避免边界效应,所以设定响应加权图r和颜色直方图特征概率图p的权重值分别为0.8和0.2。
权重计算公式如下:
r(x,y)=r3-4(x,y)+ 0.25 × r5-4(x,y)
(16)
s(x,y)=0.8 × r(x,y)+ 0.2 × p(x,y)
(17)
4 实验结果及分析
4.1 实验数据集介绍
VOT[15]数据集是评价目标跟踪方法的重要数据集之一,已经成为了跟踪领域顶会必须拿出的指标。VOT benchmark主要提供了三个部分:(1)提供了可靠的公开测试数据集;(2)规定了测试评价方法;(3)提供了可靠地评价系统。此数据集包含60个测试序列,为了达到更好的准确度以固定标准对所有序列进行了双精度标注。对每一个序列都标注出该序列的六种视觉属性:目标动作变化、遮挡、目标尺寸变化、相机移动、未退化、光照变化。该数据集提供了有关真实值的更为丰富的信息,便于研究设计更高精确度的跟踪算法,更能反映问题,已有上百个算法在此数据库上进行了公开测试,所以本文选取VOT作为测试平台。
该数据集通过期望平均覆盖率(Expected average overlap,EAO)评估跟踪算法的精确度(Accuracy)和鲁棒性(Robustness)。EAO是指跟踪器在一个序列上的非重置重叠的期望值,是VOT评估跟踪算法精度的最重要指标,值越高表示算法的性能越好。
准确率是指跟踪器在一个序列下跟踪的平均重叠率(两矩形框的相交部分面积除以两矩形框的相并部分的面积)。用来评价跟踪器的准确度,数值越大,准确度越高。它借用了交并比(Intersection-over-Union,IoU)定义,某序列第t帧的准确率定义为:
(18)
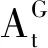
鲁棒性是指一个序列下跟踪失败的次数,当重叠率为0时认为是跟踪失败。用来评价跟踪器的稳定性,数值越大,稳定性越差。鲁棒性的计算公式。定义F(i,k)为第i个跟踪器在第k次重复中失败的次数。所以鲁棒性定义为:
(19)
4.2 实验结果分析
本文将测试结果即测试序列每帧的跟踪结果提交到VOT Challenge数据库进行测试后可得到相关性能指标。我们称本文改进算法为improved,图4显示算法在VOT 2016数据集中的测试结果,横轴坐标为序列长度,纵轴显示EAO值。红色曲线显示了本文改进算法的期望平均覆盖率EAO值随序列长度改变的变化,黄色曲线则为CF2算法的EAO值测试结果。由图可知,本文改进算法的EAO值一直高于CF2算法,可见本文改进算法一直优于CF2算法,尤其对于短时跟踪来说,改进算法表现出明显的优势。
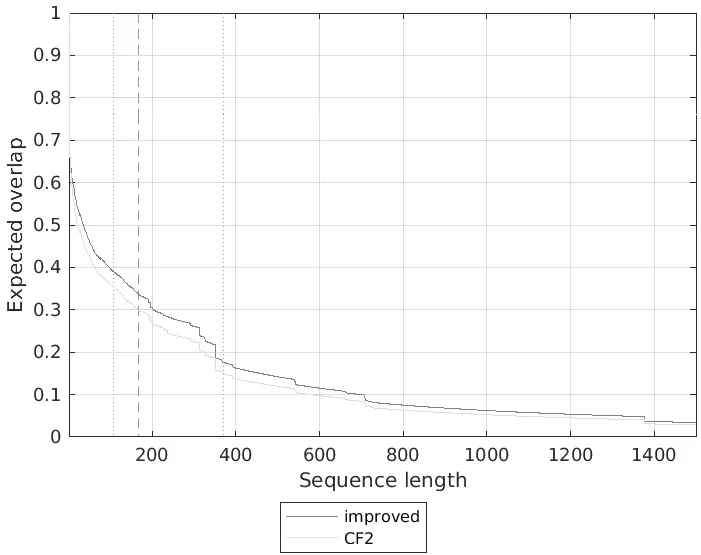
图4 EAO曲线图
表1展示了跟踪结果的数值排名表,Expected overlap列显示的是EAO的综合数值,改进算法的期望平均覆盖率为0.2655,而原算法的期望平均覆盖率为0.2543,可见本文改进算法比原算法跟踪的期望平均覆盖率更高。Accuracy列和Robustness列分别展示了EAO的两个评价指标,即精确度和鲁棒性的值,可以看到改进算法的精确度为1.03,而原算法的精确度为1.02,由此可知本文算法的精确度更高,不过改进算法的鲁棒性不如原算法。
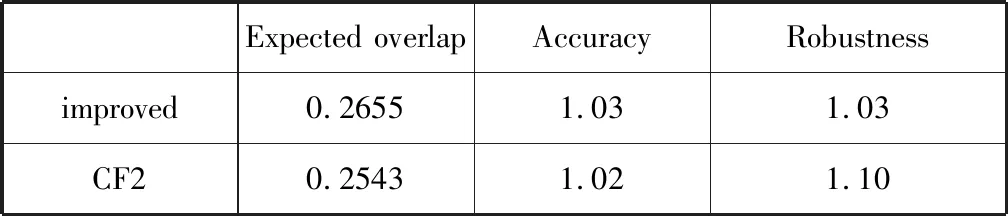
表1 EAO跟踪结果数值表
为了进一步测试本文算法的性能,我们分别对不同属性的序列进行跟踪测试。如图5所示,展示了六种属性的EAO值,从左往右,从上到下,依次是动作变化、遮挡、尺寸变化、相机移动、未退化、光照变化属性。可见当图像序列表现出动作变化、尺寸变化、相机移动、未退化的属性时,改进算法表现优异,而这些属性正好是造成边界效应的原因,所以实验证明融合的特征模板可以有效地解决相关滤波算法的边界效应问题。并且通过比较图中的数据可见,本文算法对于短时跟踪情况比CF2算法性能更突出,可以认为本文算法更适合短时间跟踪。
为了更直观的体现算法的改进效果,我们分别从主观和客观两方面对比具体序列的跟踪效果。表2对比了本文算法和CF2算法在VOT 2016数据集部分测试序列的精确度的客观评价结果,而表3为本文算法和CF2算法在VOT 2016数据集部分测试序列测试结果的可视化示意图,根据示意图做主观评价,红色的框表示官方给定的目标位置真值框,绿色的框表示两种算法跟踪的结果框。由图表中可以看到本文算法具体的改进结果,具体证明了改进算法的有效性。
例如,对于视频序列hand来说,本文算法的精确度为0.544,而CF2算法的精确度为0.452。在可视化图中,可以看到在第23帧时,两算法都能正确跟踪目标,但是由于目标运动过快,在第47帧时,CF2算法已经不能准确的进行跟踪了,到了第66帧时CF2算法丢失目标,然而本文算法能够一直正确跟踪目标,并保持较高的跟踪精确度。由此可以得出结论,本文算法能够解决边界效应问题。
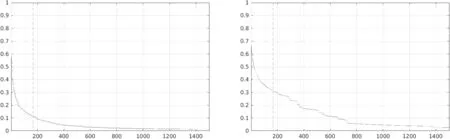
(1)动作变化 (2)遮挡
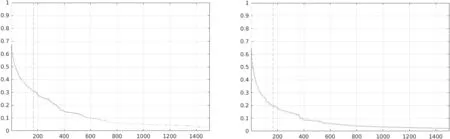
(3)尺寸变化 (4)相机移动
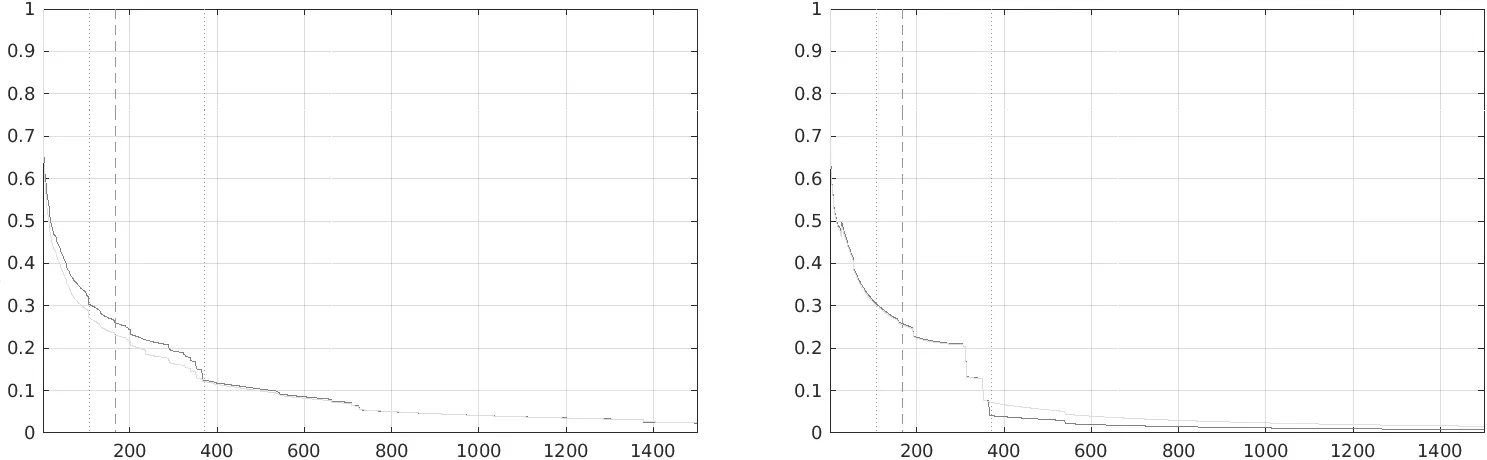
(5)未退化 (6)光照变化图5 六种属性的EAO曲线图
表2 VOT 2016数据集部分测试序列测试结果

序列精确度Pedestrian1Handball2Bolt1gloveSinger3matrixhandimproved0.7170.4860.4660.5100.2540.5400.544CF20.7030.4640.3960.5010.1670.5130.452序列精确度Pedestrian2basketballFish1sheepSoccer2girlBirds1improved0.5330.6520.4230.6340.5320.6100.490CF20.4690.6460.4140.6260.4850.6010.459
对于视频序列Singer3来说,改进算法的精确度为0.354,而CF2算法的精确度为0.167。在第5帧时两算法能够正确跟踪目标,当是到第66帧时,目标发生尺寸和形状上的改变,影响了两算法的跟踪结果,到了第113帧的时候,目标又发生形变,此时CF2算法跟踪目标失败,但是本文算法能够正常并稳定的进行跟踪。由此可得出结论:本文算法能够应对目标形变的问题。

表3 VOT 2016数据集部分测试序列测试结果示意图
5 结论
本文针对基于相关滤波的跟踪算法具有边界效应的问题,提出一种基于特征模型融合的相关滤波目标跟踪算法。该算法利用卷积神经网络提取深度特征,进行相关滤波操作,得到响应图模型,同时利用传统的特征提取方式,提取颜色直方图特征概率图进行模型融合,用来弥补相关滤波算法的边界效应问题和模板类方法不能有效处理目标变形的问题。实验证明,本文算法利用较复杂的VOT数据集测试时仍可达到较为稳定的跟踪效果,并且能够提高目标跟踪的性能,达到较为理想的跟踪的效果。
尽管本文的改进算法可解决相关滤波跟踪的一些问题,并能达到较好的跟踪效果。但是由于作者水平有限以及工作时间的限制,算法还存在着一些不足,如不能有效处理目标变形的问题,且对于有光照变化的场景准确率不高,需进一步研究。
