封闭式独立柱三面板广告牌的面板极值风压

郭魁 戴益民 袁养金

摘要：目前存在的三面板广告牌形式板间存在板间缝隙，为研究缝隙对面板极值风压系数的影响，本文以模型面板1为研究对象，主要研究了模型面板1上不同区域的极小值风压系数和极大值风压系数特性，分析了板间缝隙对面板1不同区域的极值风压系数的影响。堵缝使得上风向极小值风压系数显著增大并在40°风向角附近达到最大值，缝隙的存在增大下风向边缘区域的极小值风压系数，而面板中部区域基本不受缝隙的影响。

关键词：三面板;板间缝隙;极值

0 引言

我国独立柱三面板广告牌面板结构均为非封闭式，这類结构形式的广告牌相邻面板间的高速间隙流会对第三块面板内表面受较大的风荷载作用，为了减少间隙流对面板在风荷载作用下的影响，本文通过封闭式独立柱三面板广告牌刚性模型测压试验，来研究其风压分布规律。顾明，韩志惠等，指出广告牌面板边缘处的平均风压要比其他区域大，立柱负面面板表面出现较大的脉动值。汪大海等独立柱双面板及三面板广告牌进行了刚性模型测压试验和气弹性模型测力风洞试验。在Kareem和Winterstein等研究的基础上，采用Hermite矩方法计算面板非高斯测点的极值风压，给出了面板风压分区及对应的设计参数，Ding等比较分析类非高斯风荷载效应的三种极值计算方法。

1 实验简介

1.1 风洞及风场模拟

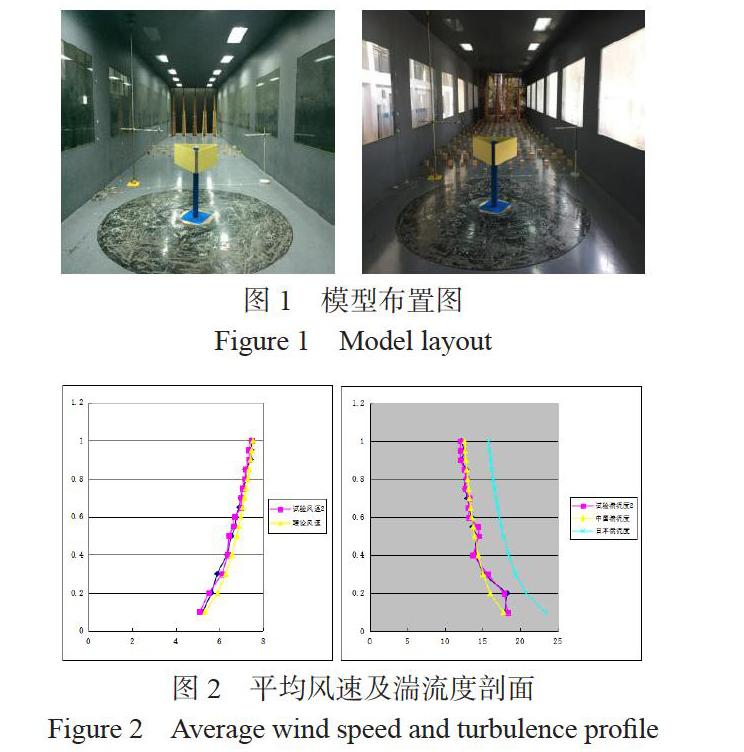
本文中三面板广告牌模型测压试验是在湖南科技大学风洞实验室中完成的。该实验室直流电动机驱动的额定功率为：315kW，额定转速为：500转/分，空风场时风场湍流度低于1.0%，风速在0 m/s-30m/s之间。试验的数据通过三维脉动风速仪、电子扫描阀系统、皮托管等对风速、风压、湍流度进行数据采集，采样频率为330HZ，采样长度为10000。

1.2 实验模型及测点布置

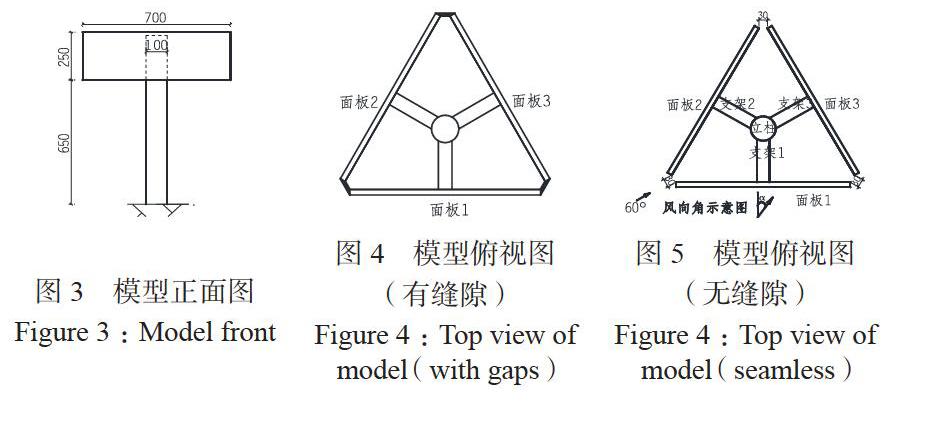
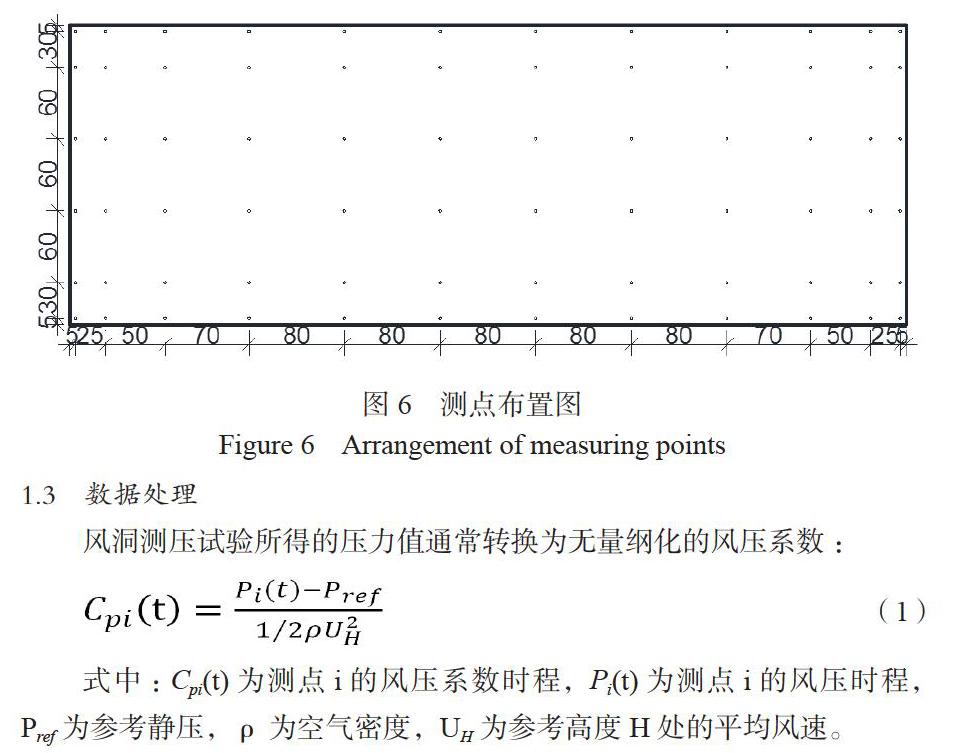
按照1：20的几何所缩尺比来设计刚性模型，模型采用薄质木盒来模拟面板，把测压管布置在木盒内的两面，通过立柱和支架与扫描阀链接，立柱采用直径为10cm的空心钢管柱，支架采用直径为5cm的空心钢管柱。由于风压在气流分离处产生明显变化，故测点采用满布对称、边密中疏的方式，共计432个测点，面板以立柱中心为对称中心对称布置：

1.3 数据处理

风洞测压试验所得的压力值通常转换为无量纲化的风压系数：

式中：Cpi（t）为测点i的风压系数时程，Pi（t）为测点i的风压时程，Pref为参考静压，ρ为空气密度，UH为参考高度H处的平均风速。

2 极值风压

2.1 极小值风压系数

由图可知，板间缝隙对外面板中部区域影响较小，基本稳定在-0.25左右。缝隙对上风向边缘区的极小值风压系数影响较小但对下风向边缘区影响较大。同时发现缝隙的存在可以降低下风向区域极小值风压系数，这是由于缝隙中间有气流通过从而降低了表面风压。堵缝使得上风向极小值风压系数显著增大并在40°风向角附近达到最大值。缝隙的存在增大下风向边缘区域的极小值风压系数，而面板中部区域基本不受缝隙的影响。

2.2 极大值风压系数

由图可知，无论缝隙存在与否下风向边缘区域极大值风压系数最大。面板1中的中部区域及上风向区域外表面极大值风压系数变化趋势基本一致，随风向角的增大而增大。而对于内表面上的中部区域极大值风压系数均大于上风向边缘区域。

3 结论

（1）堵缝使得上风向极小值风压系数显著增大并在40°风向角附近达到最大值，缝隙的存在增大下风向边缘区域的极小值风压系数，而面板中部区域基本不受缝隙的影响。

（2）当考虑面板整体所受风压时，上风向边缘区域极大值风压系数明显增大。

参考文献：

[1] 顾明，陆文强，韩志惠，等.大型户外独立柱广告牌风压分布特性[J].同济大学学报（自然科学版），2015（03）.

[2] 韩志惠，顾明.大型户外独立柱广告牌风致响应及风振系数分析[J].振动与冲击，2015（19）.

[3] 韩志惠，陆文强，顾明，等.高层建筑屋顶广告牌风致响应分析[J].振动与冲击，2018（03）.

[4] 顾明，陆文强，韩志惠，周晅毅.高层建筑屋顶广告牌风压分布特性[J].同济大学学报（自然科学版），2015（08）.

[5] 汪大海，程浩，张玉清，等.大型双面广告牌面板风压特性的试验研究[J].振动与冲击，2017（22）.

[6] 汪大海，程浩，李志豪.大型广告牌面板的非高斯风压特性及风致易损性研究[D].武汉理工大学，2009.

[7] 汪大海，李志豪，陈新中.大型单立柱双面广告牌风荷载及风振响应分析[J].哈尔滨工业大学学报，2018（06）.

[8] Kareem A， Zhao J， Tognarelli M A. Surge response statistics of tension leg platforms under wind and wave laods：a statistics quadrat ization approach [J]. Probabilistics Engineering Mechanics， 1995（04）.

[9] Winerstein， Steven R. Nonlinear Vibration Models for Extremes and Fatigue[J]. Journal of Engineering Mechanics， 1988（10）.

[10] Ding J ， Chen X Z. Assessment of methods for extreme valua analysis of non-Gaussian wind effects with short-term time history samples [J]. Engineering Structures， 2014.