储罐检测爬壁机器人全遍历路径规划

唐东林，龙再勇，汤炎锦，潘 峰，游传坤

（西南石油大学机电工程学院，四川成都610500）

路径规划是实现移动机器人精确运动和控制的核心问题之一，大量学者进行了深入研究，并取得了一定的成就［1-4］。移动机器人的路径规划主要分为2类：一类是点到点的路径规划，另一类是全遍历路径规划。点到点的路径规划是指机器人在工作环境中寻找一条从起点到终点的安全避障路径［5-7］。全遍历路径规划是指机器人规划出一条能够完全遍历环境中未被障碍物占据区域的路径，并要求所规划路径满足安全性和合理性要求［8-10］。全遍历路径规划在草坪修剪机［11］、收割机［12］、清扫机器人［13］以及军用扫雷机器人［14］中有广泛应用。

根据是否掌握工作空间的环境信息，可将全遍历路径规划分为已知环境规划和未知环境规划［15-17］。针对已知环境的路径规划，已有相对成熟的方法，且容易实现对环境的全遍历。针对未知环境的路径规划，一般采用随机遍历的方式，这种方式效率很低且无法实现全遍历。近年来未知环境遍历路径规划算法成为了研究热点。文献［18］将生物激励神经网络与启发式规则相结合，用于遍历路径规划，实现了简单环境的遍历，但不能遍历含有U型障碍物的环境和使机器人快速逃离死区。文献［19］将基于栅格地图的单元分解法用于遍历路径规划，实现了对简单结构化环境的遍历和死区逃离，但对含有各向U型障碍物的复杂环境无法实现全遍历。

本文根据储罐检测爬壁机器人工作环境的特点，提出了一种基于滚动窗口的优先级启发式算法。基于栅格地图建立储罐检测爬壁机器人工作环境模型，利用设计的优先级启发式算法在滚动窗口对路径进行搜索。引入U型障碍物区域填充算法和死区逃离算法，使机器人能有效地遍历U型障碍物区域并且快速逃离死区，降低遍历重复率，使机器人在未知储罐环境下能有效地遍历整个工作区域。

1 储罐检测爬壁机器人工作环境建模

1.1 储罐壁面简化

立式圆柱体储罐外壁是圆弧面，为三维工作环境。图1所示为储罐检测爬壁机器人壁面工作图。

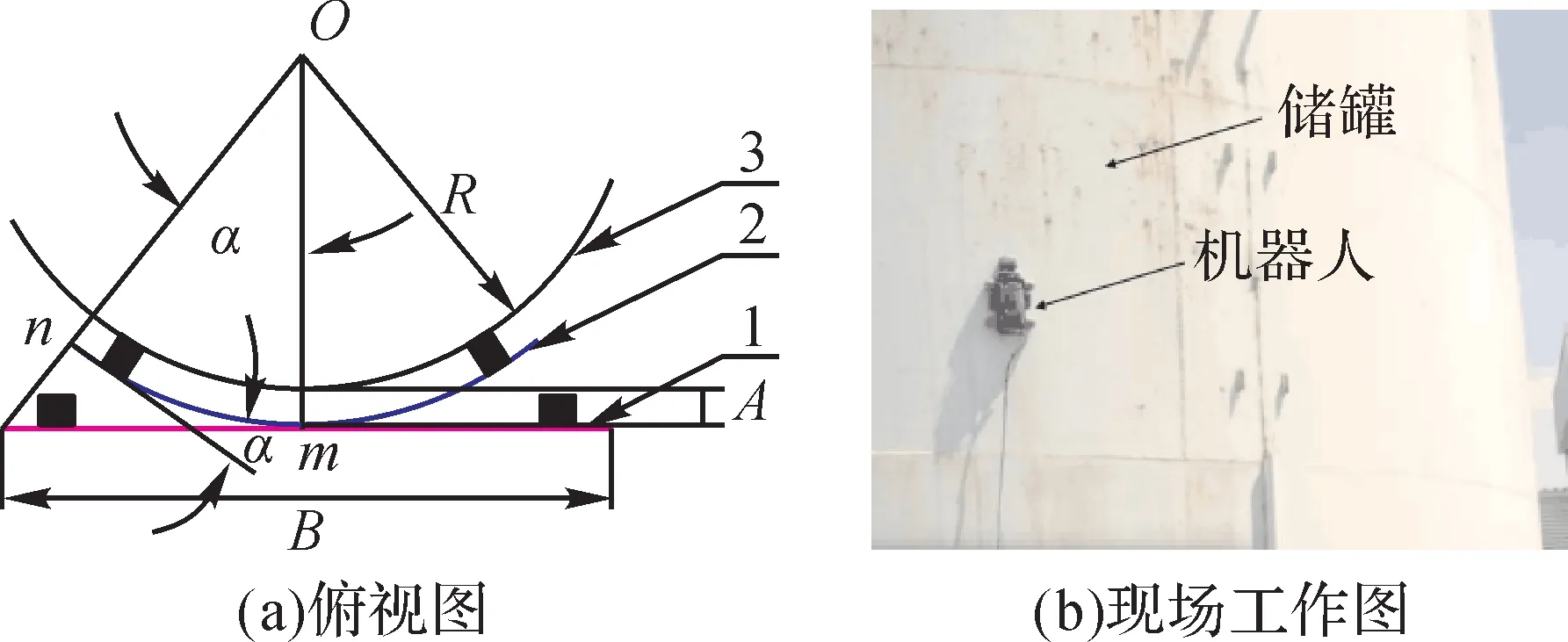
图1 储罐检测爬壁机器人壁面工作图Fig.1 Wall working diagram of oil tank detection wall climbing robot

图1（a）中：O为储罐横截面圆心；R为储罐半径；n为机器人左端点；m为机器人质心；A为机器人底板距储罐外壁距离；B为机器人宽度；α为机器人爬行后的曲率角。

常用的圆柱体储罐直径为24.0～40.0 m，高为9.6～16.3m。以直径为24.0 m、高为9.6 m 的储罐，宽度B=0.3 m的机器人（机器人底板距储罐外壁的距离A很小，可以忽略）为例，进行计算：

α代表机器人在储罐壁面爬行时的变形量。从式（1）可得：α的值很小，可忽略不计；随着储罐容积增大，α值呈降低趋势。因此机器人在储罐壁面爬行时几乎不发生变形，可将机器人看作在竖直二维平面上爬行。

1.2 基于栅格地图的环境建模

基于栅格地图对储罐外壁建模，根据机器人检测探头的宽度确定栅格大小。如式（2）所示，每个栅格有一个表示栅格状态的值xi，并随着机器人运动实时更新。

定义1：只要栅格被障碍物占据，则将该栅格定义为障碍物栅格。

根据储罐外壁的情况建立环境模型，如图2 所示，有针对性地在环境中设置了储罐外壁可能存在的障碍物。该环境的栅格地图模型如图3所示，其中黑色部分为障碍物栅格，空白部分为未遍历栅格。通过对比图2和图3可得，基于栅格地图进行环境建模可以使环境中的不规则障碍物变成规则的方形障碍物，使机器人在遍历时运动方式变得简单。

图2 储罐检测爬壁机器人工作环境模型Fig.2 Working environment model of oil tank detection wall climbing robot

图3 储罐检测爬壁机器人工作环境模型的栅格地图Fig.3 Grid map of working environment model of oil tank detection wall climbing robot

若根据栅格的赋值情况建立三维栅格地图，则未遍历栅格位于地图的顶部，已遍历栅格位于地图的中部，而障碍物栅格位于地图的底部，如图4所示。可将该方法用于基于传感器的未知环境实时局部建模。

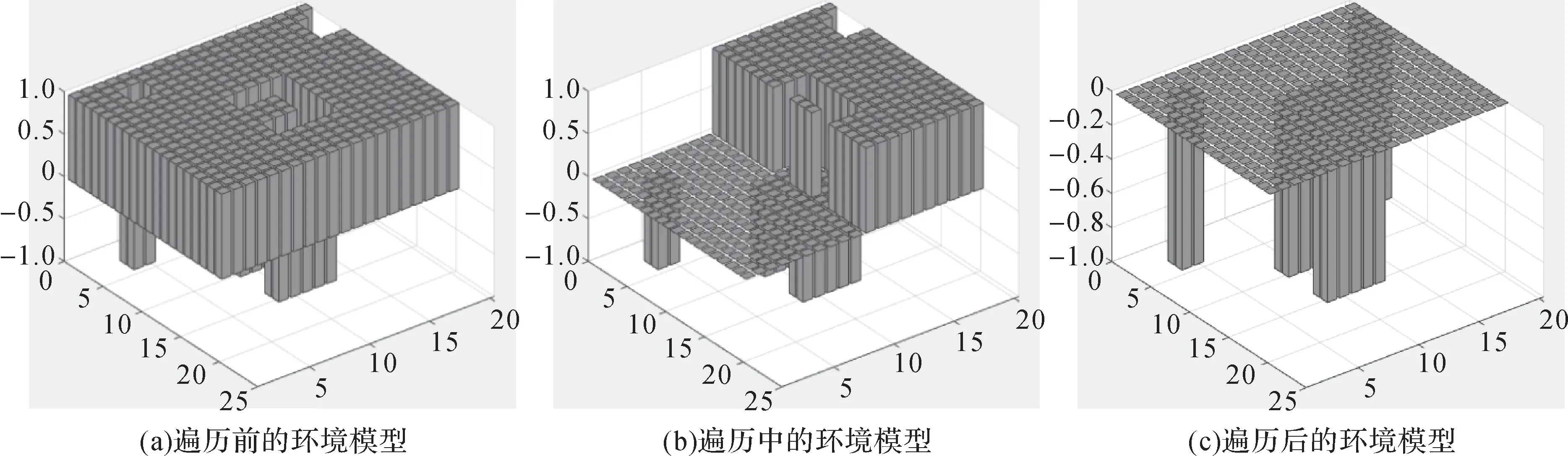
图4 储罐检测爬壁机器人工作环境模型的三维栅格地图Fig.4 3D grid map of working environment model of oil tank detection wall climbing robot

2 基于滚动窗口的遍历路径规划

2.1 路径规划描述

本文讨论的是储罐全局环境未知情况下爬壁机器人全遍历路径规划问题。规划的目的是机器人能遍历工作环境中所有可达区域，并满足遍历重复率最小的要求［20］。

储罐外壁分布着有限个大小、形状不受限制的障碍物，机器人事先未存储任何障碍物信息，只能利用搭载的传感器探测有限范围内的环境信息。为了安全起见，在机器人在线探测时把障碍物作一定的膨化处理［21］，同时机器人具有存储运动路径信息和自定位功能。将机器人视为一个质点，当它运动到地图中的某个栅格时，认为该栅格已遍历。

2.2 基于滚动窗口的优先级启发式路径规划

图5所示为基于滚动窗口的优先级启发式路径规划算法的构建流程。

图5 基于滚动窗口的优先级启发式路径规划算法的构建流程Fig.5 Construction flowchart of priority heuristic path planning algorithm based on rolling window

2.2.1 滚动窗口

基于滚动窗口的路径规划（简称滚动规划）是机器人在工作空间运动过程中实时探测周围的局部环境信息，并以逐步滚动的方式进行在线路径规划，可实现路径的优化与反馈，确保规划算法的合理性和安全性。

在滚动规划中定义的滚动窗口包括可视窗口和规划窗口。滚动窗口的生成包括以下4个步骤：

1）设置滚动窗口的参考坐标系。

如图6所示，XOY表示世界坐标系，xoy表示机器人坐标系。机器人利用其携带的传感器探测障碍物的位置信息，在xoy坐标系中建立局部环境模型，用该坐标系中的坐标来表示障碍物的具体位置。机器人在全局环境中的位置则需要用XOY坐标系的坐标来表示，通过XOY与xoy的坐标变换则可以确定障碍物在XOY坐标系中的具体位置，从而建立全局环境模型。

图6 滚动窗口参考坐标系Fig.6 Rolling window reference coordinate system

2）确定滚动窗口的范围。

设W表示机器人所在二维平面所有点的集合，P表示环境中的任意一点，PXY(t)表示机器人当前时刻位置，d表示机器人当前时刻位置与环境中任意一点的距离。机器人传感器能够探测以机器人为中心、半径为r的圆形区域环境信息。

定义2：Win(PXY(t))={P|P∈W，d(P，PXY(t))≤r}为机器人的滚动窗口。

3）确定可视窗口。

可视窗口是在滚动窗口的基础上设定的，在不影响局部路径规划的前提下，考虑局部环境信息的存储及计算量，选取合适的滚动窗口大小。

定义3：以机器人为中心的5×5 个栅格为可视窗口。

4）确定规划窗口。

规划窗口是机器人进行局部路径规划的区域，其大小不能超过可视窗口，且需根据局部路径规划算法确定。根据优先级启发式路径规划算法，以机器人前进1个单位长度来定义规划窗口。

定义4：以机器人为中心的3×3 个栅格为规划窗口。

如图7 所示，可视窗口和规划窗口分别包含24个和8个栅格的信息。机器人在规划窗口内确定局部子目标并规划路径向子目标行进。机器人每行进1 步，窗口相应向前滚动，搭载的传感器将实时获得最新的环境信息并对滚动窗口进行更新。如图8所示，Rob1、Rob2、Rob3 分别表示机器人移动时的位置，r1、r2、r3为相对应的滚动窗口的半径。

图7 滚动窗口Fig.7 Rolling window

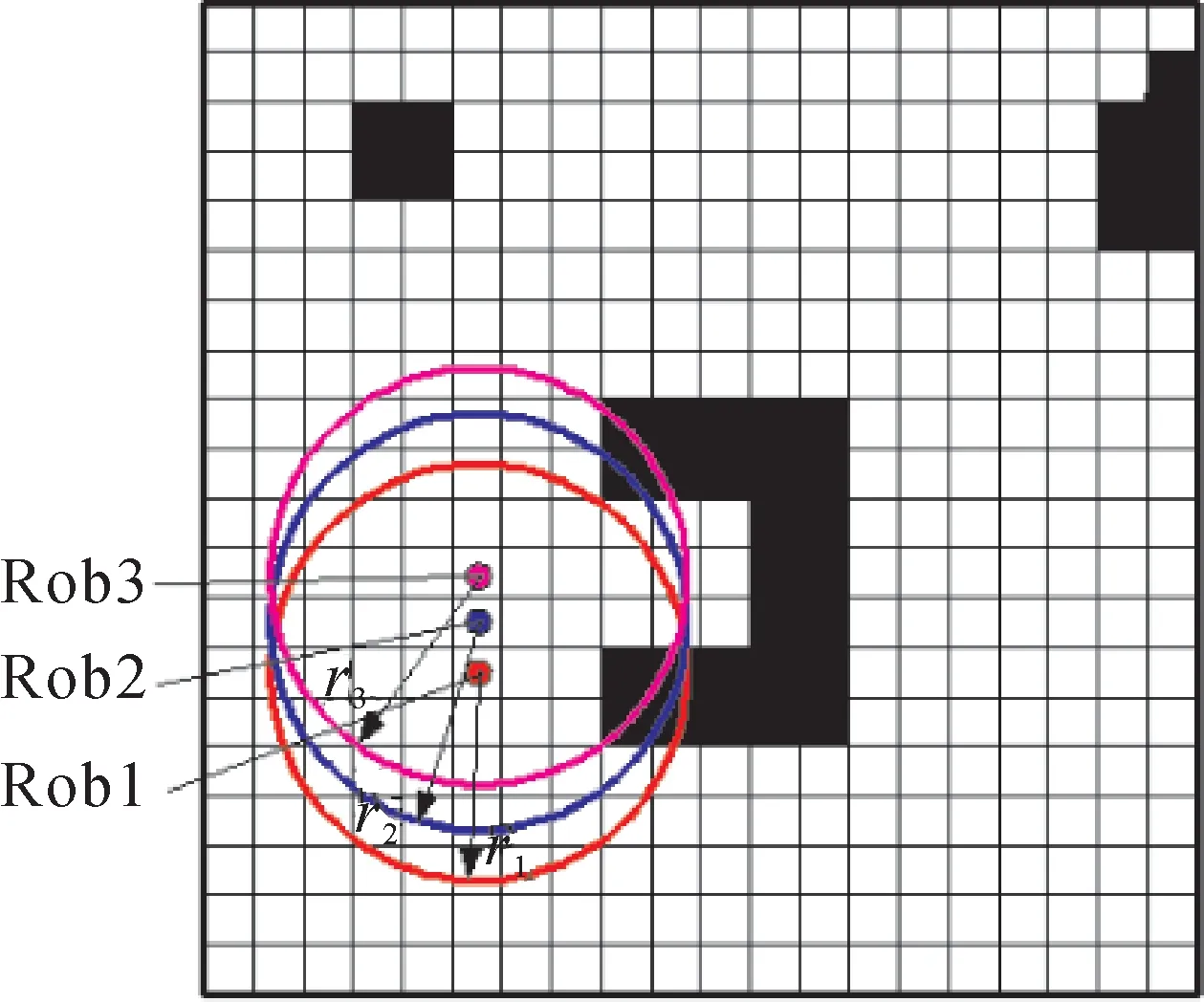
图8 窗口滚动示意图Fig.8 Schematic diagram of window rolling

2.2.2 优先级启发式算法设计

启发式算法是与具体问题求解及搜索过程相关的，将求解问题的具体信息融入算法中，从而提高算法的搜索效率，具有简单、直观且有效的优点。因此本文提出基于滚动窗口的优先级启发式算法，将启发式算法运用在路径规划以提高路径搜索的时空效率。

本文提出的基于滚动窗口的优先级启发式算法，是根据建立的环境模型在以机器人为中心的规划窗口内设计优先级顺序，确定邻域栅格搜索的优先级，从而规划出合理的局部遍历路径。

如何结合可视窗口的环境信息和路径规划的具体要求设计合理的优先级顺序是整个路径规划的关键。本文设计的优先级顺序为：PX-1，Y（左栅格）、PX，Y-1（下栅格）、PX，Y+1（上栅格）、PX+1，Y（右栅格）、PX+1，Y-1（右下栅格）、PX+1，Y+1（右上栅格）、PX-1，Y-1（左下栅格）、PX-1，Y+1（左上栅格）。如果PX-1，Y的栅格属性值xi=1，则优先遍历PX-1，Y；如果PX-1，Y的栅格属性值xi≠1（即xi=0 或xi=-1），则 考 虑PX，Y-1。以 此 类 推，再 考 虑PX，Y+1、PX+1，Y、PX+1，Y-1、PX+1，Y+1、PX-1，Y-1，PX-1，Y+1。

若以栅格形式表示优先级顺序，则形成了如图9所示由9个栅格组成的优先级启发式算法的优先级顺序。中心栅格为机器人所在位置，其相邻栅格搜索时的优先级由所在栅格的罗马数字表示，数字I表示最先搜索，Ⅱ次之，其他依此类推。

图9 以栅格形式表示的优先级启发式算法优先级顺序Fig.9 Priority order of priority heuristic algorithm represented by grid

图10为优先级启发式算法遍历规划示意图，图中的1，2，3表示栅格遍历的顺序。当机器人在位置1时，在规划窗口按照上述算法建立优先级顺序，如图中规划窗口1所示。此时，机器人右侧的栅格优先级最大，因此机器人向右侧栅格行进1步，移动到图中的位置2。同理当机器人在位置2时，建立优先级顺序，如图中规划窗口2所示，机器人正下方的栅格优先级最大，机器人移动到图中的位置3，以此类推。

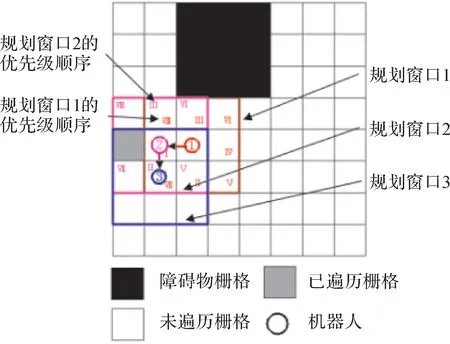
图10 优先级启发式算法遍历规划示意图Fig.10 Diagram of priority heuristic algorithm coverage planning

基于滚动窗口的优先级启发式路径规划算法的流程如图11所示。优先级启发式算法实际上是一个先左后右、先下后上的迂回式遍历规划。如图12所示，该算法不仅能完成对环境的迂回遍历，还能实现机器人的障碍物边缘行为策略的功能［22］，完成对障碍物边缘的处理，避免机器人频繁陷入死区，有效地提高路径搜索的时空效率。

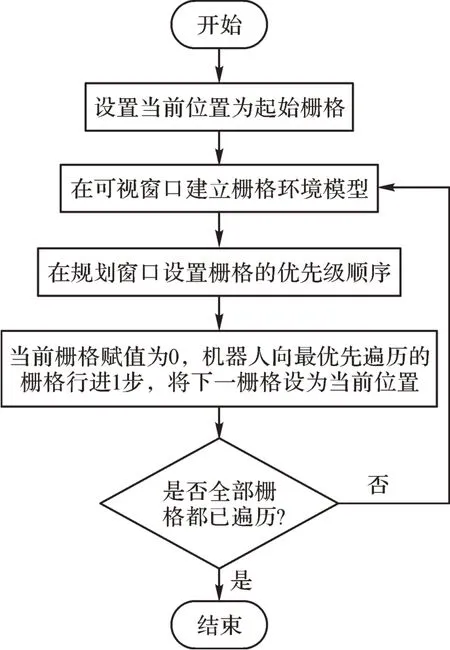
图11 基于滚动窗口的优先级启发式算法流程Fig.11 Flowchart of priority heuristic algorithm based on rolling window

图12 优先级启发式算法遍历规划实例Fig.12 Example of priority heuristic algorithm coverage planning

2.3 U型障碍物区域填充算法

储罐外壁的真实环境是比较复杂的，可能存在向内凹的U 型障碍物，如图13 所示为开口向左的U型障碍物。直接采用优先级启发式算法对含有该类型障碍物的环境进行遍历，规划的路径将从障碍物的左侧栅格经过，U型障碍物内部将无法覆盖，造成遍历不完全。因此针对该问题，本文设计了U型障碍物区域填充算法。实现U型障碍物区域的填充包括U型障碍物的识别和U 型障碍物区域直接填充两个方面。

2.3.1 U型障碍物的识别

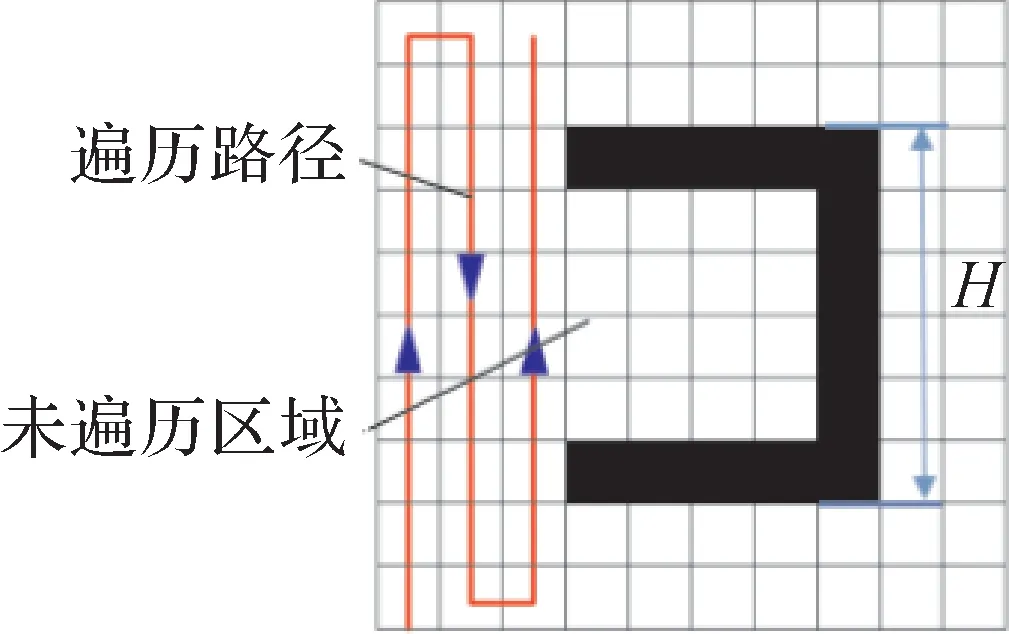
图13 开口向左的U型障碍物Fig.13 U-shaped obstacles opening to left

机器人只能通过传感器探测周围的环境，其最大探测范围为可视化窗口的大小。U型障碍物分为小型U型障碍物和大型U型障碍物两种。设H表示U型障碍物的开口宽度（用栅格数表示大小），可视窗口的大小为5个。

定义5：H≤5 个时，为小型U 型障碍物；H＞5 个时，为大型U型障碍物。

1）小型U型障碍物的识别。

如图14所示，当机器人在G点时，在可视窗口内可观察到障碍物点L、I，记录两障碍物点的位置信息。当机器人在C点时，如果在可视窗口的右上方存在连续障碍物，则可确定该障碍物为U型障碍物。

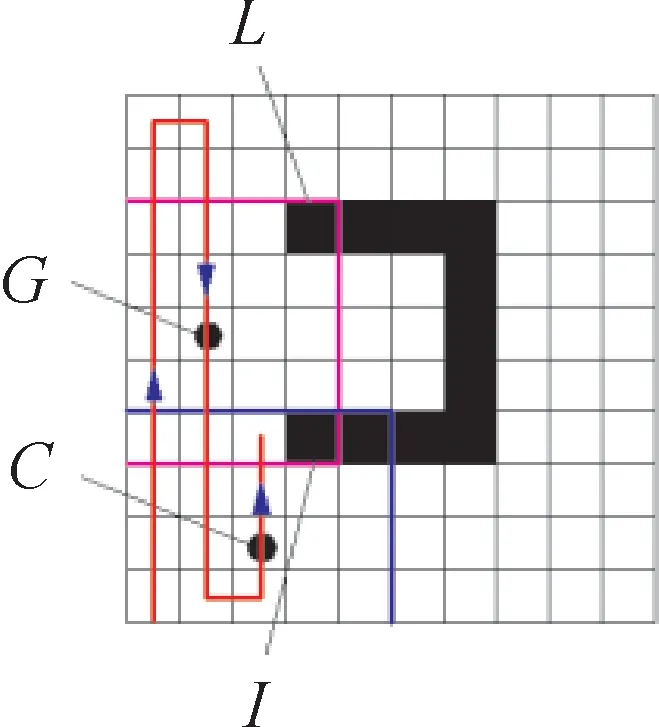
图14 小型U型障碍物的识别Fig.14 Identification of small U-shaped obstacles

2）大型U型障碍物的识别。

如图15所示，当机器人运动到D、E两点所在栅格时，在可视窗口内可观察到障碍物点J、K，记录两障碍物点的位置信息。当机器人在F点时，如果在可视窗口右上方有连续障碍物，则可确定该障碍物为U型障碍物。

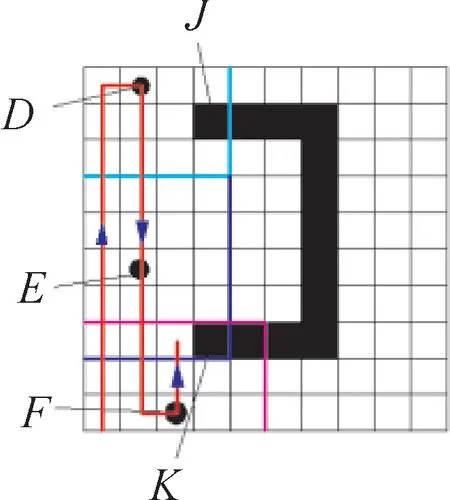
图15 大型U型障碍物的识别Fig.15 Identification of large U-shaped obstacles

2.3.2 U型障碍物区域直接填充

为了对图13所示的U型障碍物区域进行直接填充，机器人的运动路径需向右延伸，因此在确定规划窗口栅格的遍历顺序时，应使机器人右侧相邻栅格的优先级最高。以栅格形式表示遍历的优先级顺序，本文设计了如图16所示的优先级启发式算法优先级顺序，可实现对U 型障碍物区域直接填充。图17 为U型障碍物区域直接填充的实例。

图16 U 型障碍物区域直接填充的优先级启发式算法优先级顺序Fig.16 Priority order of priority heuristic algorithm for direct filling of U-shaped obstacle area

图17 U型障碍物区域直接填充实例Fig.17 Example of direct filling of U-shaped obstacles area

根据上述的方法识别U 型障碍物可能会出现2种判断结果：U型障碍物和2条平行的障碍物带。如果是2条平行的障碍物带，如图18所示，采用U型障碍物区域直接填充算法会造成规划路径的不合理，因此引入虚拟U 型障碍物的概念，当机器人向右填充时，若规划窗口的右侧和右下（上）侧均为未遍历栅格时（如图19（a）所示），便把右侧栅格当作虚拟障碍物，如图19（b）所示。

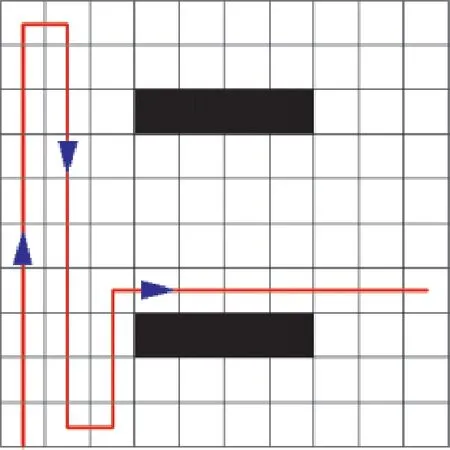
图18 2条平行的障碍物带Fig.18 Two parallel obstacles

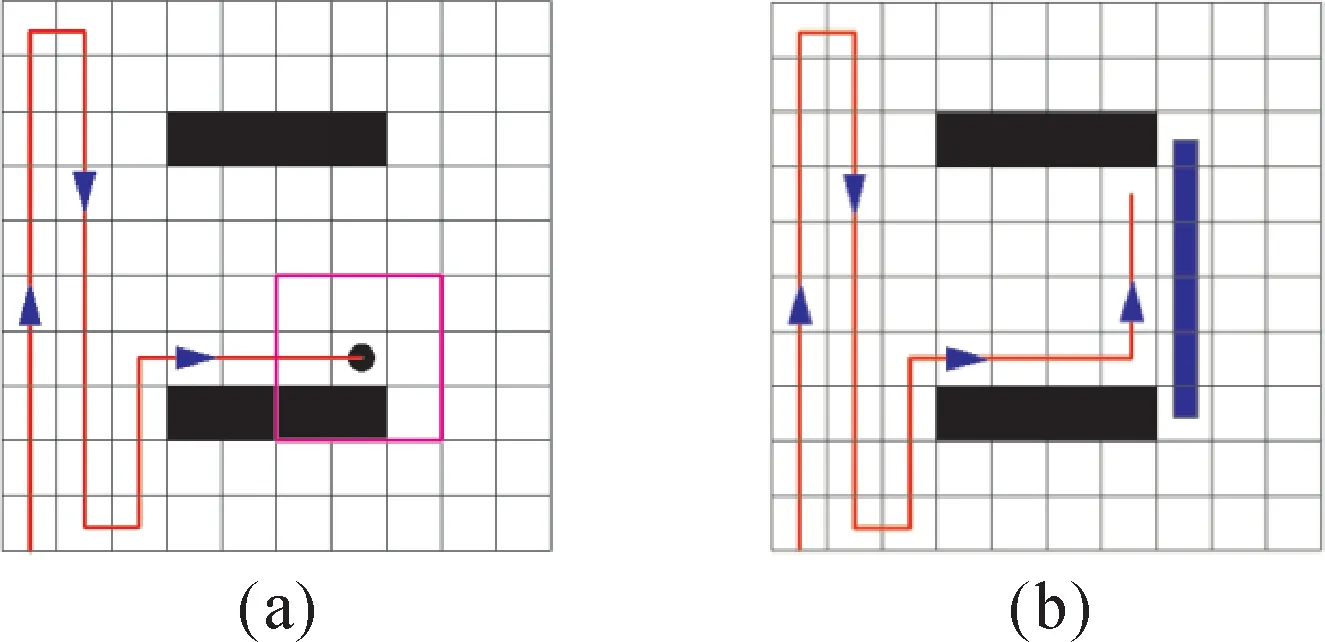
图19 虚拟障碍物的识别Fig.19 Identification of virtual obstacles

另外，采用优先级启发式算法可以对如图20所示环境中其他开口方向的U型障碍物区域进行填充，因此不需要单独设计直接填充算法。

图20 其他开口方向U型障碍物区域的填充Fig.20 Filling of U-shaped obstacle area opening to other directions

2.4 死区逃离算法

如图21所示，当储罐检测爬壁机器人周围栅格均为障碍物、边界或已遍历栅格时，机器人陷入死区。

图21 储罐检测爬壁机器人陷入死区Fig.21 Oil tank detection wall climbing robot falling into the dead zone

机器人陷入死区后，无法再采用优先级启发式算法进行局部路径规划，则应让机器人尽快以最优路径逃离死区。因此引入了方向函数yi，如图22所示，引导机器人快速逃离死区，其定义为：

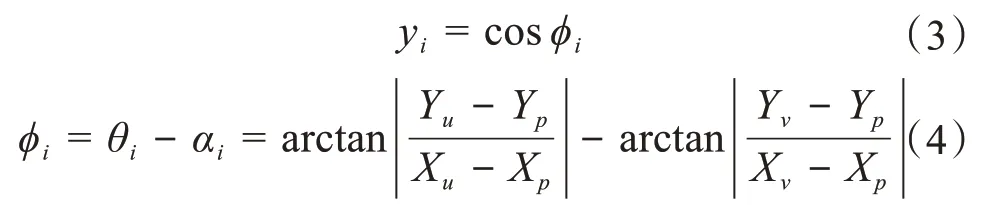
式（4）中：(Xp，Yp)为机器人当前位置坐标；（Xv，Yv）为机器人下一步移动位置坐标；（Xu，Yu）为距机器人当前栅格最近的未遍历栅格坐标；φi为机器人当前栅格和最近未遍历栅格连线与机器人当前栅格和下一步移动栅格连线的夹角；θi为机器人当前栅格和最近未遍历栅格连线与X轴的夹角；αi为机器人当前栅格和下一步移动栅格连线与X轴的夹角。

为了使机器人以合理的路径逃离死区，仅仅依靠方向函数是无法实现的，引入了一个路径选择函数fi，其定义为：

路径选择函数不仅仅包含了方向函数，还加入了栅格的属性值xi，c是一个权值常数，0＜c＜1。

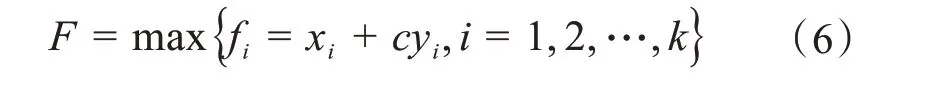
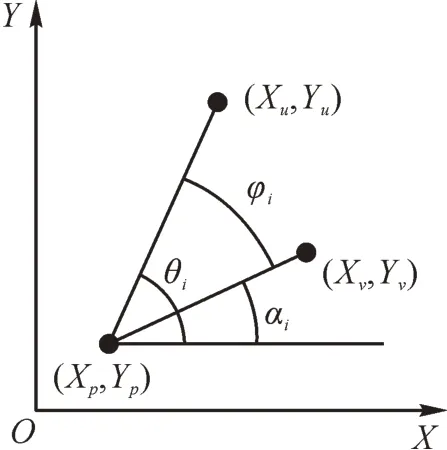
图22 储罐检测爬壁机器人逃离死区方向函数示意图Fig.22 Schematic diagram of direction function of oil tank detection wall climbing robot escaping from dead zone

式中：F表示路径选择函数最大值；k表示与机器人相邻栅格的个数。

机器人根据相邻栅格的路径选择函数值，逃离死区时始终往路径函数值最大的方向移动。因此可得图21中机器人陷入死区时的具体逃离路径，如图23所示。

综上所述，在储罐检测爬壁机器人未知储罐工作环境下基于滚动窗口的全遍历路径规划算法的流程如图24所示。

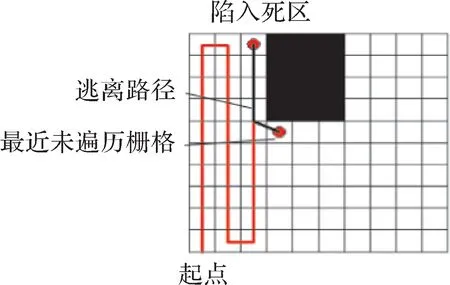
图23 储罐检测爬壁机器人逃离死区的路径Fig.23 Path of oil tank detection wall climbing robot escaping from dead zone

3 全遍历路径规划仿真试验和分析

为了检验基于滚动窗口的全遍历路径规划算法的正确性，本文进行了仿真试验，如图25所示。

仿真环境为由25×20个栅格组成的栅格地图，环境中含有储罐外壁可能存在的障碍物，自由栅格数为457 个。储罐检测爬壁机器人最初不具备任何环境的信息，只能利用其自身携带的传感器实时探测周围的局部环境，进行在线局部环境建模和滚动路径规划。

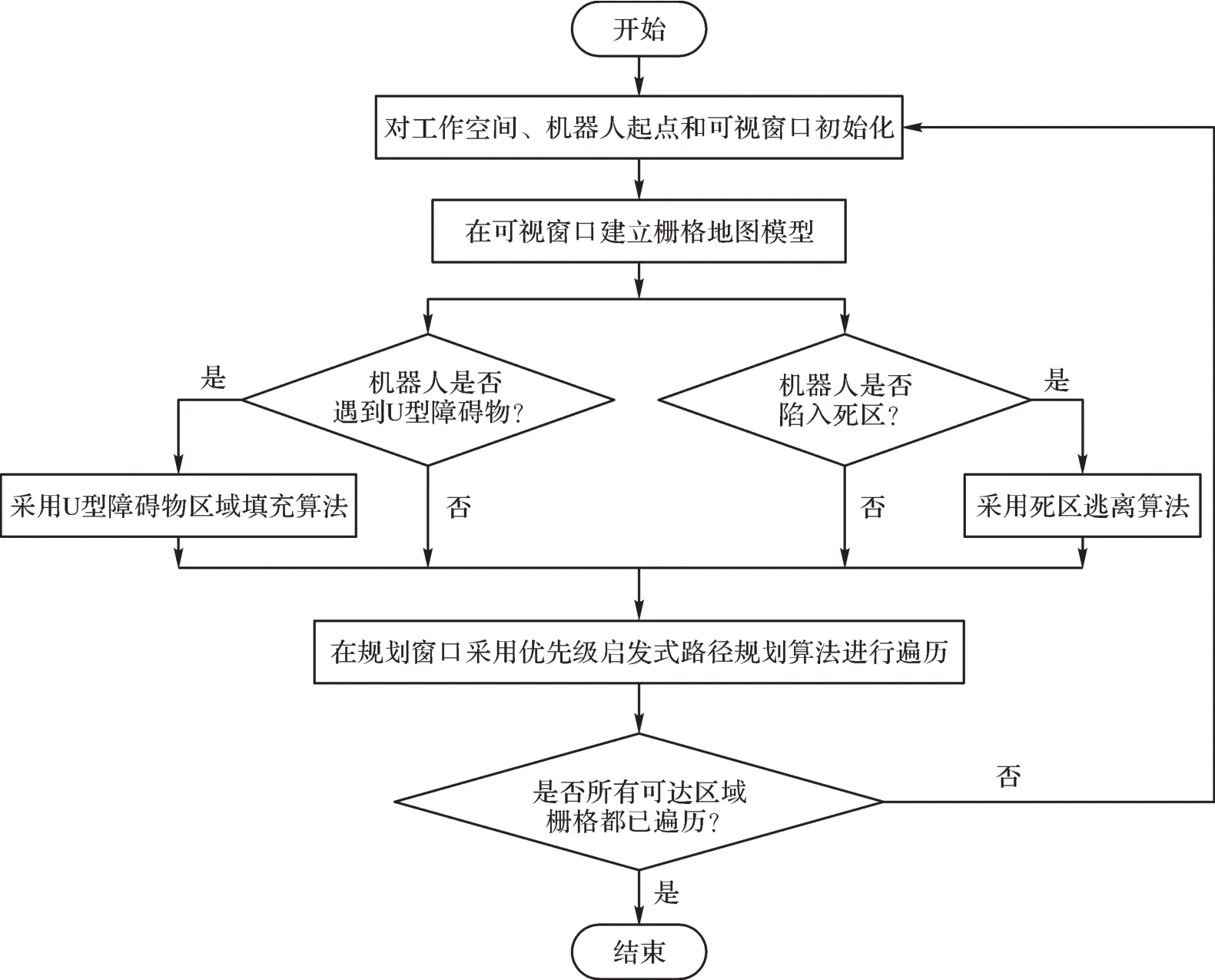
图24 基于滚动窗口的全遍历路径规划算法流程Fig.24 Flowchart of complete coverage path planning algorithm based on rolling window

图25中空白栅格为未遍历栅格，黑色栅格为障碍物。以栅格地图的左下角为起点，机器人利用滚动的可视窗口环境信息和优先级启发式算法进行在线规划。通过对（6，6）、（7，6）、（6，11）三点的判断，识别U 型障碍物，采用U 型障碍物区域填充算法进行遍历，避免了栅格的漏检。当运动到（7，20）时，周围区域均为障碍物、边界和已遍历栅格，机器人陷入死区。此时采用死区逃离算法，机器人运动到最近未遍历的栅格（8，17），逃离死区。当运动到（17，3）时，遇到2条平行的障碍物带，启用虚拟障碍物和U型障碍物区域填充算法进行填充。填充完毕后继续采用优先级启发式算法进行遍历，直到完成区域全遍历。

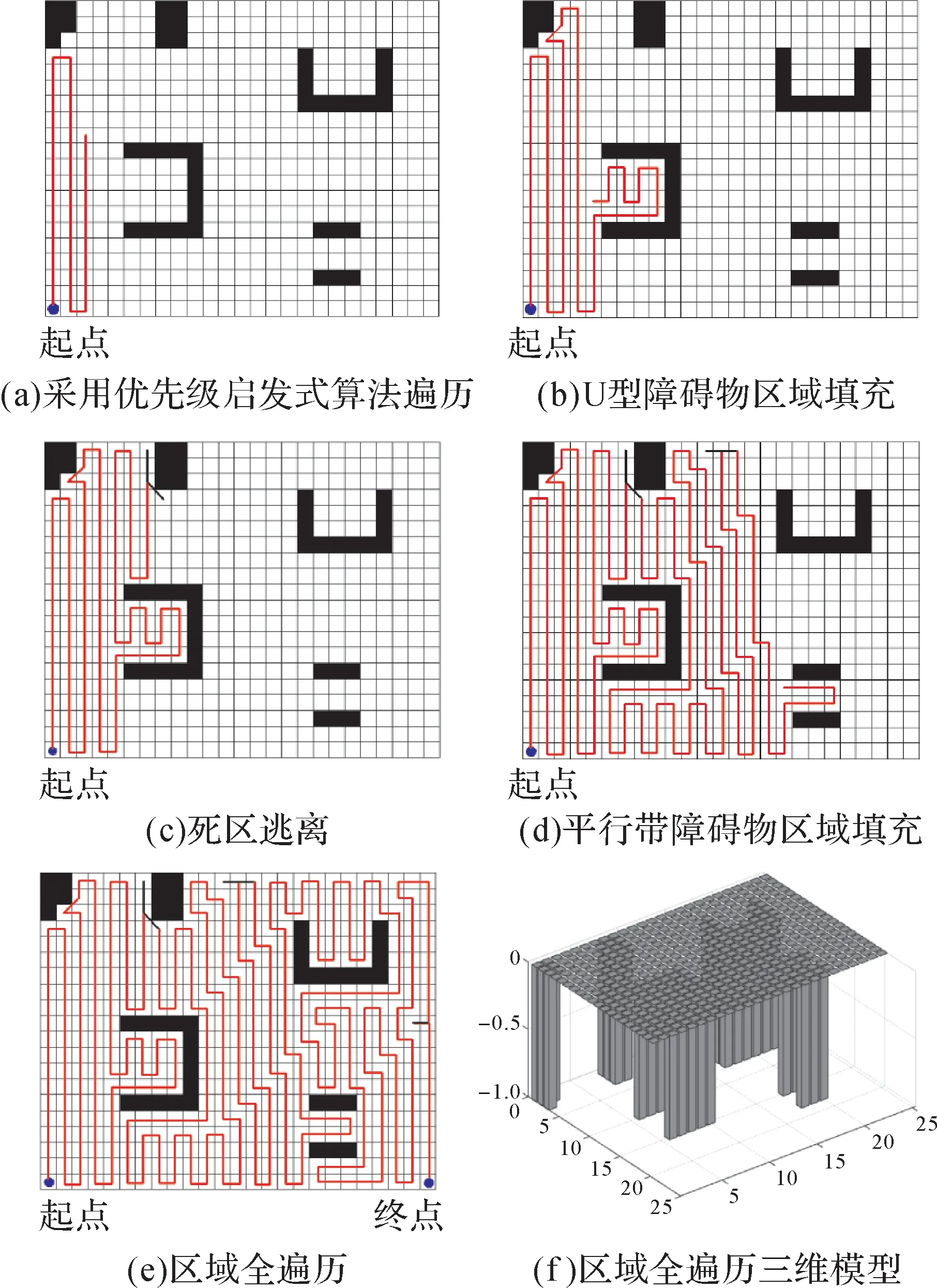
图25 基于滚动窗口的全遍历路径规划仿真试验Fig.25 Simulation test of complete coverage path planning based on rolling window

定义已遍历栅格数与可达栅格数之比为遍历率，重复遍历栅格数与可达栅格数之比为重复遍历率。在同样的环境下采用基于栅格地图的单元分解遍历路径规划算法进行仿真，结果如图26所示，表明该方法针对复杂环境无法实现全遍历且遍历重复率较高。

图26 基于栅格地图的单元分解遍历路径规划仿真结果Fig.26 Simulation result of unit decomposition coverage path planning based on grid map

从图25、图26中可以得出不同算法下机器人遍历性能评价指标，如表1所示。

由表1可知：基于栅格地图的单元分解遍历路径规划方法不能实现对环境的全遍历，遍历率为95%，重复率为4%，转弯数为148次；本文提出的基于滚动窗口的全遍历路径规划方法能很好地实现对工作空间的遍历，遍历率达100%，重复率为0.88%，转弯次数为136次。

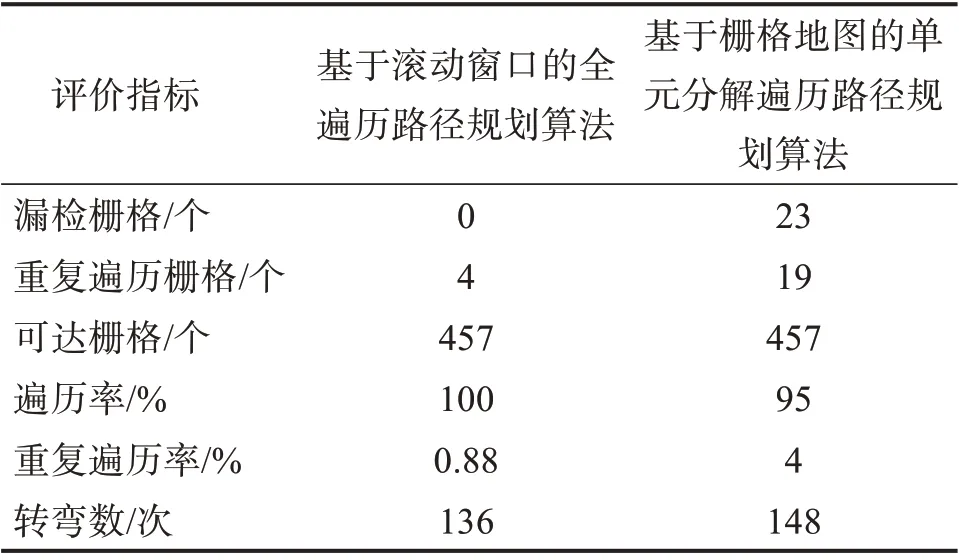
表1 不同算法下储罐检测爬壁机器人遍历性能评价指标Table 1 Coverage performance evaluation index of oil tank detection wall climbing robot under different algorithms

同时，为验证基于滚动窗口的全遍历路径规划算法在不同环境下的鲁棒性，选择不同环境对算法进行测试。在3种大小及内部障碍物均不同的环境下的路径规划仿真结果如图27所示。从图中可以看出，随着环境变大、变复杂，路径也越复杂，机器人陷入死区的次数增多：在15×15个和20×20个栅格环境下，机器人陷入死区的次数均为2次；在30×30个栅格环境中，机器人陷入死区的次数达到了5次。机器人陷入死区的次数越多，重复遍历的栅格越多。但在3种环境下，本文算法都能对U型障碍物、平行障碍物带和陷入死区进行处理，最终都能实现机器人工作区域的全遍历。不同环境下机器人遍历性能评价指标如表2所示。

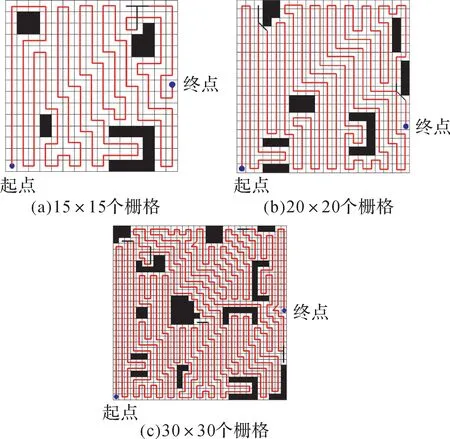
图27 不同环境下基于滚动窗口的全遍历路径规划仿真结果Fig.27 Simulation results of complete coverage path planning based on rolling window in different environments

表2 不同环境下储罐检测爬壁机器人遍历性能评价指标Table 2 Coverage performance evaluation index of oil tank detection wall climbing robot in different environments

4 结 论

本文采用基于滚动窗口的优先级启发式路径规划算法，实现了储罐检测爬壁机器人在未知储罐外壁环境情况下对工作区域的全遍历。利用滚动的可视窗口环境信息和设计的优先级启发式遍历算法，实现机器人对工作空间的迂回遍历；提出U型障碍物区域填充算法和虚拟障碍物概念，实现U型障碍区域的连续遍历；当机器人陷入死区时，快速启用死区逃离算法以使机器人逃离死区。仿真结果表明该方法能够实现机器人对储罐外壁的全遍历，降低了遍历重复率，整体上提高了遍历效率。