5 000 m3立式拱顶储罐应力分析与弱顶性能评价

李成兵，雷 鹏

（1.西南石油大学机电工程学院，四川成都610500；2.西南石油大学石油天然气装备教育部重点实验室，四川成都610500）

随着我国石油化工行业的不断发展，拱顶储罐因低造价、易操作而得到广泛应用［1］。有研究表明［2-3］，储罐发生火灾时，弱顶结构储罐的罐顶与罐壁在其连接处脱离，储罐及时释放内压，使罐顶以下结构保存完好，而非弱顶结构储罐会整体倾倒并报废。因此，为了减少因内部超压而引发的安全事故，通常将储罐设计成弱顶结构，即罐顶和罐壁连接处采用弱连接，使得储罐内部发生超压时，顶壁连接焊缝先于其他部位破坏，从而及时泄压，防止事故扩大化，达到减少人员伤亡和财产损失的目的［4-6］。

目前已有许多学者对储罐弱顶结构进行研究。刘巨保等［7-9］利用有限元法分析了拱顶储罐在不同工况下的应力，提出通过改变罐顶曲率半径和顶板厚度来使储罐满足弱连接定义；对比基于国内外3种标准设计的弱顶结构，得到了3种弱顶结构的差别；研究了20 000 m3大容量网壳顶储罐的应力分布，并提出了实现网壳顶储罐弱顶性能的方法。刘明等［10］研究了4种边界条件下罐体的应力分布和罐底的接触状态，提出通过锚固措施来限制储罐罐底提离。丁宇奇等［11］以3 000 m3立式拱顶储罐为研究对象，计算了3种工况下储罐的应力分布，并探讨了将该类储罐设计成弱顶的可能性。Hu等［12］研究了在爆炸载荷作用下储罐容积、罐顶形式等因素对固定顶储罐结构应力大小和分布的影响。邱水才等［13］通过电镜分析和数值模拟发现，拱顶罐失效形式为韧性断裂，且储罐最大应力分布在弱顶结构处。此外，黄晓明、尹晔昕等［14-15］采用简化结构即忽略焊缝结构，对储罐弱顶结构进行研究，但采用该方法往往会导致计算结果不准确，无法准确反映焊缝区的应力分布情况。

现有文献对弱顶结构研究主要参考GB 50341—2003《立式圆筒形钢制焊接油罐设计规范》［16］，而很少应用最新的GB 50341—2014《立式圆筒形钢制焊接油罐设计规范》［17］。为此，以工程上较为常用的5 000 m3立式拱顶储罐为例，依据GB 50341—2014，对其结构进行设计，并判断是否满足GB 50341—2014中弱顶结构的设计要求；利用ANSYS建立储罐有限元模型，分析其应力分布、强度状况以及弱连接强度比等；通过改变储罐的主要结构参数，探讨实现储罐具备弱顶性能的方法，旨在为拱顶储罐弱顶结构的改进提供依据。

1 储罐结构设计及弱顶性能评价

1.1 储罐结构参数设计

根据GB 50341—2014，5 000 m³立式拱顶储罐选用Q235-B 钢，其屈服应力为225 MPa，许用应力为150 MPa。储罐直径为20 000 mm，高度为17 820 mm，罐壁板由10 层壁板组成，每层壁板的高度为1 780 mm，自底往上壁板的厚度分别取为13，11，10，9，8，7，6，6，6，6 mm，罐顶曲率半径为24 000 mm，罐顶厚度为6 mm，罐顶焊角高度为4 mm，中幅板厚度为8 mm，边缘板厚度为11 mm，包边角钢型号选用∠75 mm×75 mm×10 mm。地基由外侧的混凝土圈梁和内部的回填砂组成。

1.2 储罐弱顶结构设计要求

GB 50341—2014 规定［17］，直径不小于15 000 mm的储罐采用弱连接结构连接罐顶与罐壁时，应满足：连接处的罐顶坡度不大于1/6；罐顶支撑构件不与顶板相连；顶板与包边角钢仅在外侧连续角焊，焊脚尺寸不大于5 mm，内侧不得焊接；连接结构在对接、搭接时应满足：

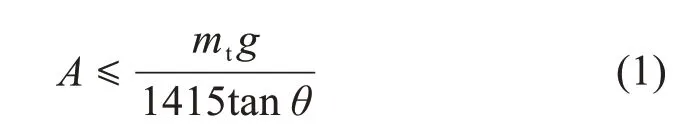
式中：A为罐顶与罐壁连接处的有效截面积，mm2；mt为罐壁和由罐壁、罐顶支撑的构件（不包括罐顶板）的质量，kg；θ为罐顶与罐壁连接处罐顶与水平面的夹角，（°）；g为重力加速度，取9.81 m/s2。

1.3 储罐弱顶性能评价

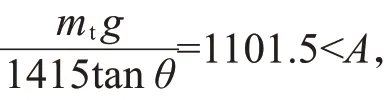
2 储罐有限元分析模型的建立

拱顶储罐径厚比很大，属于薄壁圆柱壳结构。在进行应力分析时，不可忽略罐顶与包边角钢、罐壁与边缘板的连接焊缝对结构强度的影响，同时还需考虑整体结构失稳的临界压力，以得出储罐的破坏形式。故分别建立拱顶储罐的轴对称有限元模型及空间有限元模型，以进行强度分析与稳定性分析。

取任一轴对称面为研究对象，采用PLANE82建立拱顶储罐罐体和地基的轴对称有限元模型，其中：回填砂半径为9 850 mm，高度假定为1 500 mm，混凝土圈梁内径为9 850 mm、外径为10 150 mm，高度假定为1 500 mm；罐底和地基接触面采用CONTA172 和TARGE169 接触单元；模型共划分为6 782个单元和22 124个节点；地基底面施加全约束，模型对称轴处设定轴对称边界条件。储罐强度分析有限元模型如图1（a）所示。在进行储罐稳定性分析时，地基的影响可忽略，取整个储罐为研究对象，建立储罐空间有限元模型，采用SHELL181 壳单元划分网格，共划分为2 912个单元和3 120个节点；对罐底板下表面施加全约束。储罐稳定性分析有限元模型如图1（b）所示。

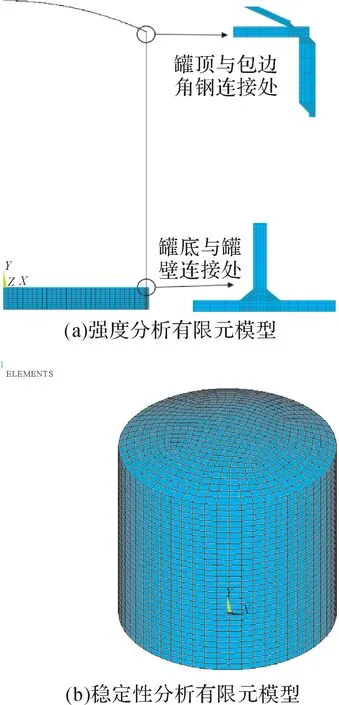
图1 储罐有限元模型Fig.1 Finite element model of storage tank

3 储罐有限元计算结果及分析

3.1 储罐强度分析

选取3种典型的液面高度，将工况分为空罐、半罐和满罐三种工况。空罐工况下储罐受静压及罐体自重的影响，半罐和满罐工况下储罐受静压、相应储液产生的梯度压力及罐体自重的影响，其中储液密度为840 kg/m3。

基于储罐强度分析有限元模型，得到空罐工况下罐顶破坏压力为4.32 kPa时储罐的应力分析结果和提离状况，分别如图2至图5所示。由图2可知，储罐的等效应力范围为0～288.894 MPa。由图3可知，储罐的最大环向应力为126.626 MPa，出现在顶壁连接处。由图4（a）可知，顶壁连接处的最大等效应力为288.894 MPa，出现在罐顶与包边角钢连接焊缝处，该值大于材料屈服强度，故顶壁连接处将发生强度破坏。由图4（b）可知，罐壁的最大等效应力为115.313 MPa，出现在底层壁板处。由图4（c）可知，罐底与罐壁连接处的最大等效应力为184.234 MPa，出现在罐底板与罐壁连接的内侧大角焊缝处。由图5可知，罐底板在半径为7 746.5 mm处发生提离，在半径为10 000 mm处达到最大提离高度，为66.5 mm。

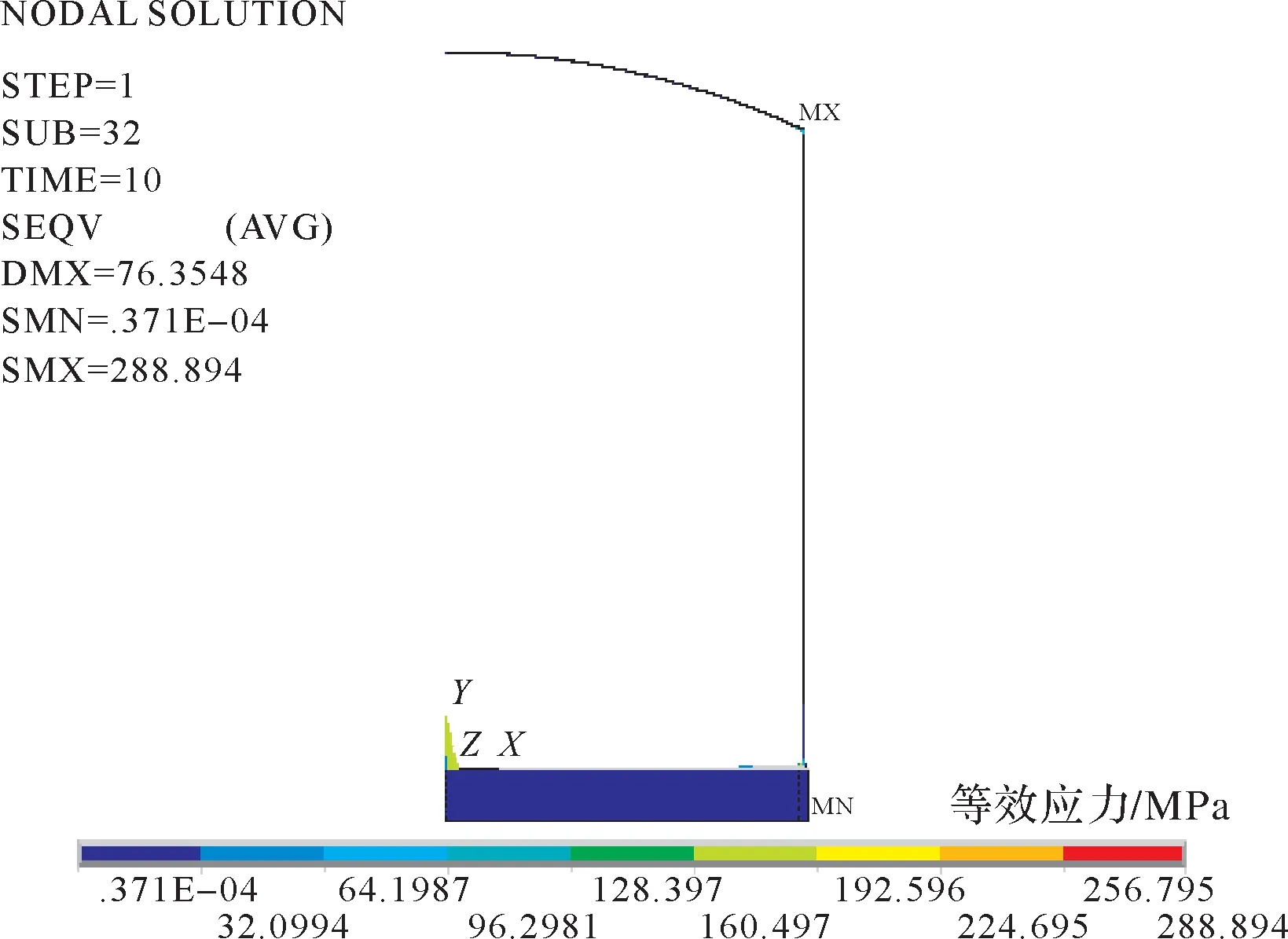
图2 空罐工况下储罐的等效应力Fig.2 Equivalent stress of storage tank under empty tank condition

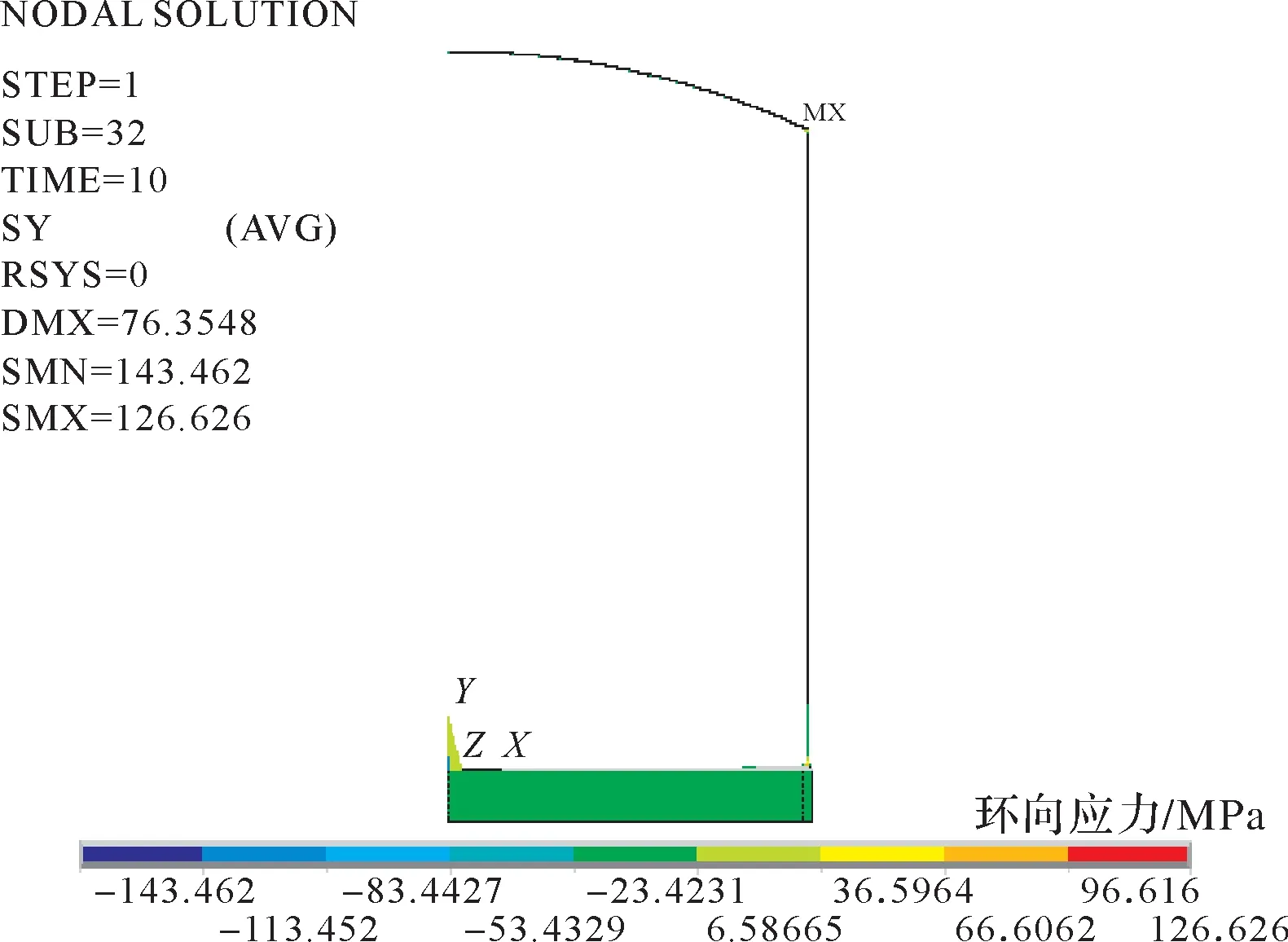
图3 空罐工况下储罐的环向应力Fig.3 Hoop stress of storage tank under empty tank condition

为判断储罐的强度状况，依据JB 4732—1995［18］中的应力分类法对储罐的一次局部薄膜应力、薄膜加弯曲应力进行计算，并由此评定储罐的强度。结合储罐的应力分布情况，选取危险截面，确定应力评定路径1、路径2 和路径3，3 条路径分别位于顶壁连接焊缝处、一二层壁板连接处、底壁连接内侧焊缝处，如图6所示。

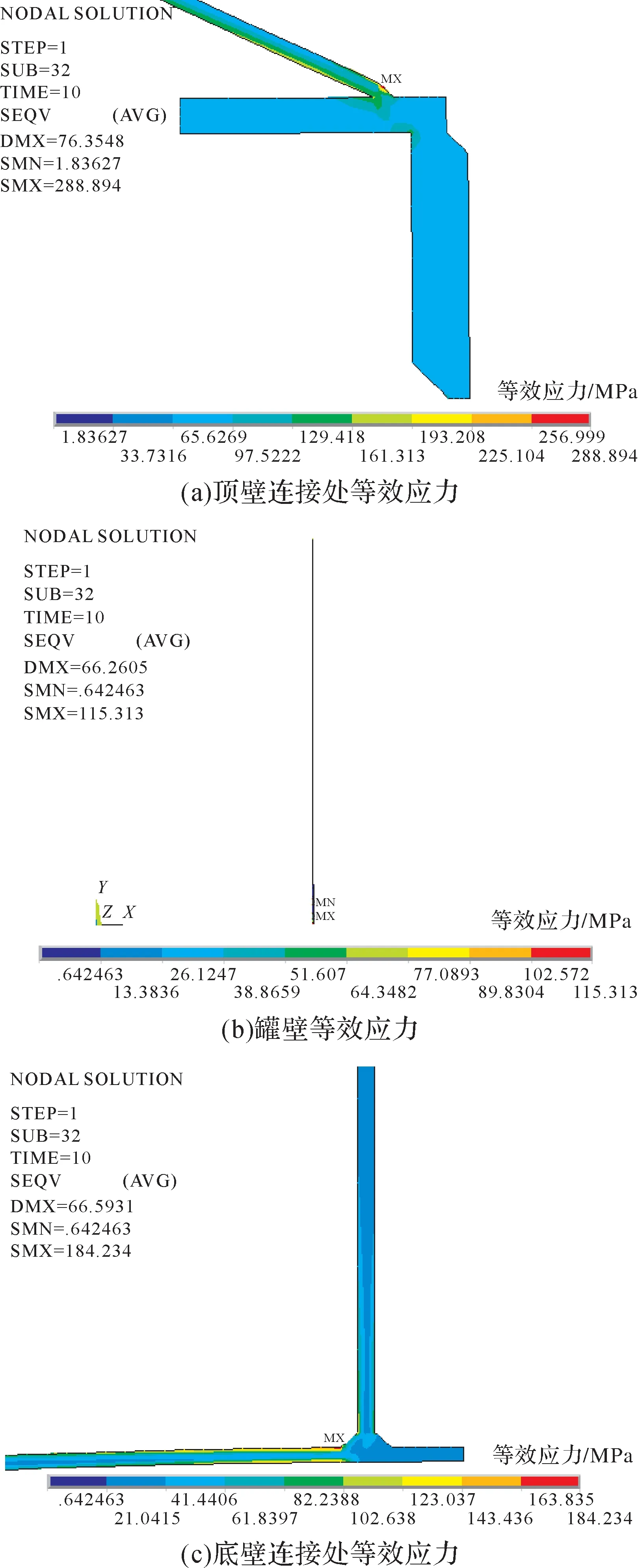
图4 空罐工况下储罐各部件的等效应力Fig.4 Equivalent stress of storage tank components under empty tank condition

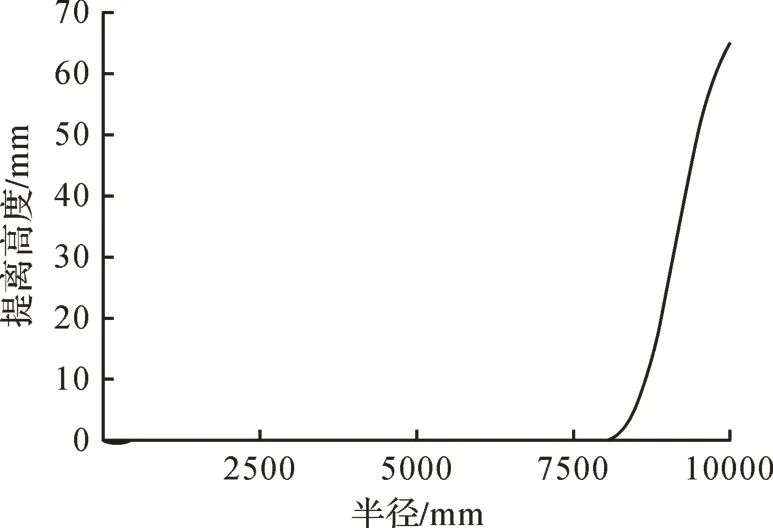
图5 空罐工况下罐底板提离高度沿径向的变化曲线Fig.5 Change curve of lifting height of tank bottom plate along radial direction under empty tank condition

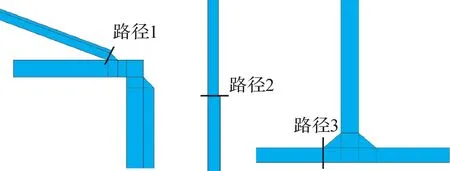
图6 储罐危险截面评定路径Fig.6 Dangerous section assessment paths of storage tank

结合储罐强度分析有限元模型和危险截面评定路径，得出在罐顶破坏压力作用下，3 种工况下储罐的提离状况、应力及强度评定结果，如表1所示。

由表1可知，各工况下储罐最大等效应力均位于顶壁连接焊缝处，且相差不大。因储液重力作用，罐壁最大等效应力随液位高度增大而增大。空罐工况下，罐底发生了较大的提离，因此该处等效应力较大；半罐和满罐工况下，储液重力作用限制了罐底提离，故这2种工况下罐底最大等效应力较空罐工况小，但储液作用导致满罐工况下罐底最大等效应力比半罐工况大；除顶壁连接焊缝处发生强度破坏外，其余部位均满足强度要求。

3.2 储罐稳定性分析

压力容器失稳是指所受载荷超过临界值时容器失去原有规则几何形状的现象。由图3可知，拱顶储罐顶壁连接焊缝处易产生较大的环向应力。由于抗压环始终位于储液液面上方，抗压环的稳定性不受工况影响，因此只需考虑储罐内压而不用考虑储液静压作用。选取空罐工况下储罐空间有限元模型进行储罐失稳模态分析，结果如图7所示。由图7可知，当罐顶临界失稳压力为5.731 kPa时，顶壁连接处开始出现失稳波形，即顶壁连接处出现失稳破坏。

图7 储罐失稳模态Fig.7 Instability mode of storage tank

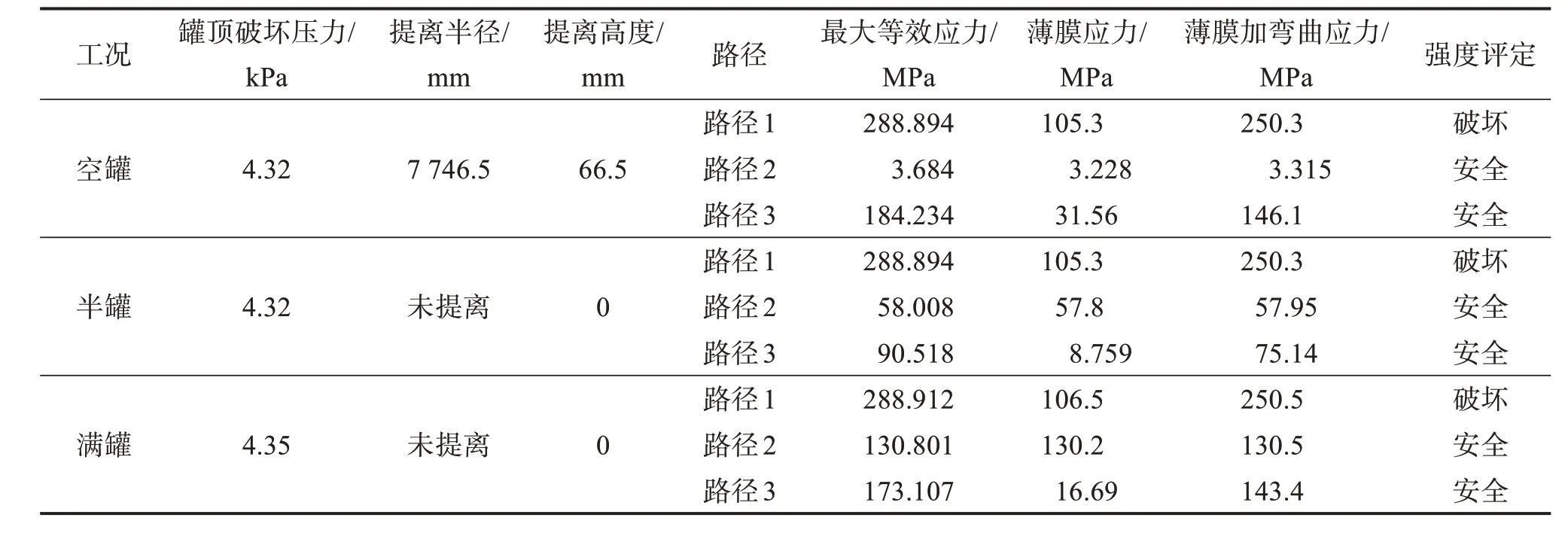
表1 3种工况下储罐的提离状况、应力及强度评定结果Table 1 Lifting conditions, stress and strength evaluation results of storage tank under three working conditions

3.3 储罐破坏形式

由3.1和3.2节分析可知，在空罐和半罐工况下，储罐顶壁连接处发生强度破坏的压力为4.32 kPa，满罐工况下为4.35 kPa，均小于储罐顶壁连接处的失稳压力（稳定性破坏压力）5.731 kPa，由此可知罐顶应先发生强度破坏。

3.4 储罐弱顶性能评价

为了判定上述拱顶储罐是否满足弱顶结构性能要求，基于储罐强度分析有限元模型及API 650［19］中的弱顶结构评价标准对该储罐的弱顶性能进行评价。API 650 建议采用弱连接强度比对储罐弱连接结构进行评价，其计算式为：

式中：Pbot为底壁连接区域破坏压力，Ptop为顶壁连接区域破坏压力。

API 650指出当储罐为弱顶结构时，空罐工况下K≥1.5，满罐工况下K≥2.5。

对储罐强度分析有限元模型进行分析，得到各工况下储罐的底壁连接区域破坏压力、顶壁连接区域破坏压力及弱连接强度比，如表2所示。

表2 不同工况下储罐弱顶性能评价结果Table 2 Weak roof performance evaluation result of storage tank underdifferent working conditions

由表2可得，空罐工况下弱连接强度比为1.3（小于1.5），满罐工况下弱连接强度比为2.2（小于2.5）。由此可知，该储罐不具备弱顶性能。

4 储罐弱顶性能提升方法分析

为了得到上述拱顶储罐弱顶性能的提升方法，结合弱连接强度比的影响因素，分析顶壁连接焊角高度、罐顶曲率半径、边缘板厚度及罐体高径比等参数对储罐弱顶性能的影响。鉴于判断弱顶性能是依据空罐和满罐工况下的弱连接强度比，且半罐工况下弱连接强度比介于空罐和满罐工况下弱连接强度比之间，故以下分析仅针对空罐和满罐工况。

4.1 顶壁连接焊角高度对弱顶性能的影响分析

取顶壁连接焊角高度为3.50，3.75，4.00，4.25 和4.50 mm，得到在罐顶破坏压力作用下，储罐各部件的最大等效应力随顶壁连接焊角高度的变化情况，如图8所示。不同顶壁连接焊角高度下储罐的弱顶性能如表3所示。

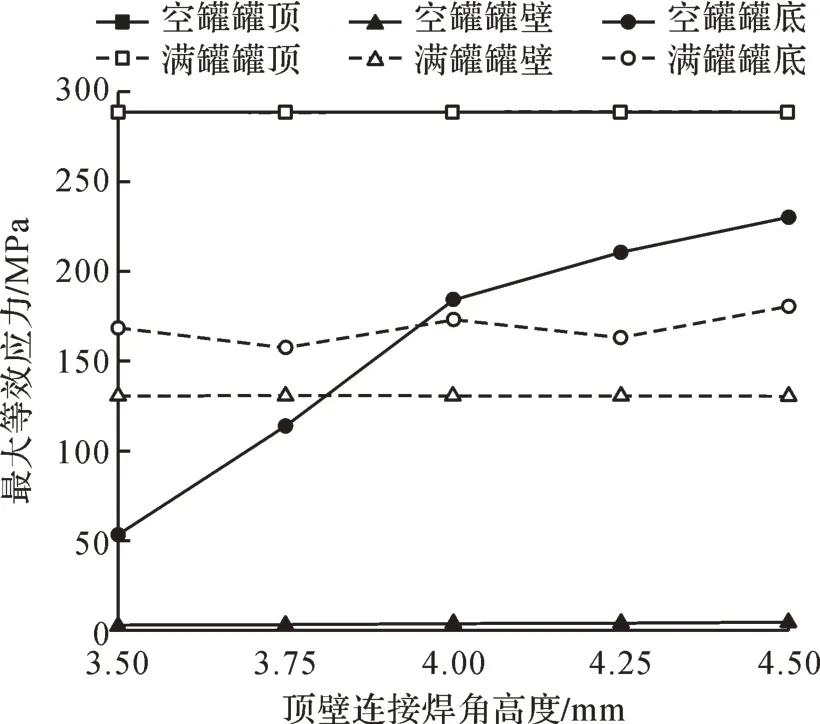
图8 不同顶壁连接焊角高度下储罐各部件的最大等效应力Fig.8 Maximum equivalent stress of each component of storage tank with different roof-wall connection weld angles heights

由图8可知：随着顶壁连接焊角高度的增大，罐顶和罐壁的最大等效应力基本不变；空罐工况下罐底的最大等效应力逐渐增大，当顶壁连接焊角高度为4.5 mm 时，空罐工况下罐底的最大等效应力超过材料屈服应力；满罐工况下罐底的最大等效应力处于较小的变化区间内。

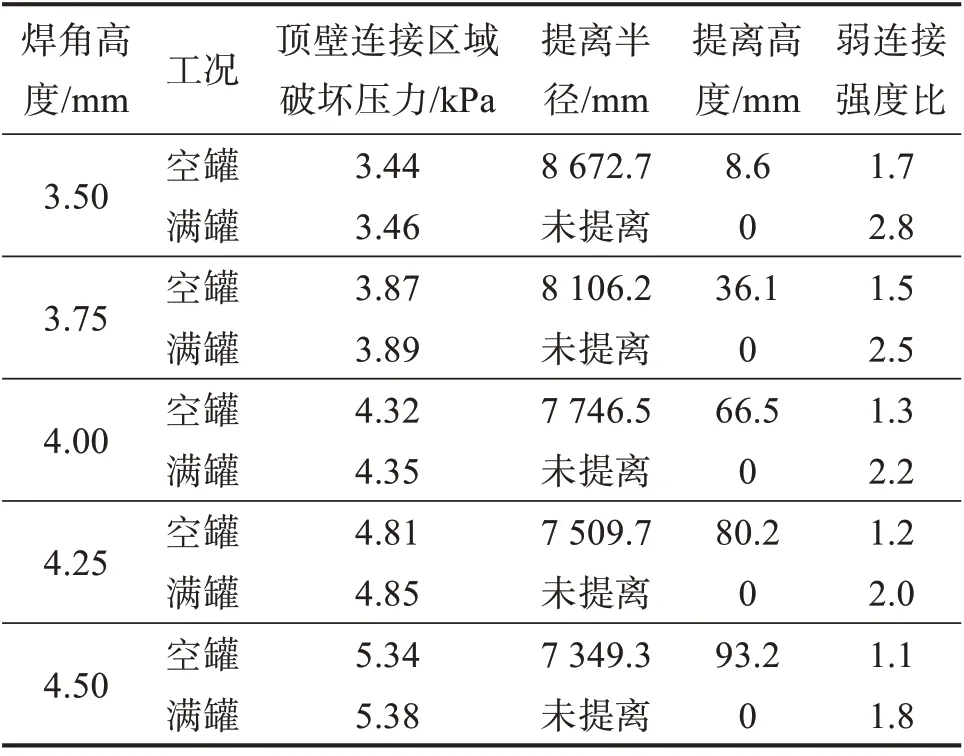
表3 不同顶壁连接焊角高度下储罐的弱顶性能Table 3 Weak roof performance of storage tank with different roof-wall connection weld angle heights

由表3可知：随着顶壁连接焊角高度的增大，顶壁连接区域破坏压力逐渐增大；罐底提离仅在空罐工况下发生，且顶壁连接焊角高度越大，罐底提离半径越小，而提离高度越大；各工况下储罐的弱连接强度比随顶壁连接焊角高度的增大而减小，且当顶壁连接焊角高度减小到3.75 mm 及以下时，储罐具备弱顶性能。

综合图8和表3结果可得，适当减小顶壁连接焊角高度能提升储罐的弱顶性能，使它满足弱顶结构的设计要求，但需注意该方式会降低储罐承压能力。

4.2 罐顶曲率半径对弱顶性能的影响分析

取罐顶曲率半径为1.2D，1.5D，2.0D，3.0D和4.0D（D为储罐直径），得到在罐顶破坏压力作用下储罐各部件的最大等效应力随罐顶曲率半径的变化情况，如图9所示。不同罐顶曲率半径下储罐的弱顶性能如表4所示。

由图9可知：随着罐顶曲率半径的增大，罐顶和罐壁的最大等效应力基本不变；当罐顶曲率半径为1.2D～2.0D时，空罐工况下罐底的最大等效应力急剧减小，当罐顶曲率半径大于2.0D后，空罐工况下罐底的最大等效应力变化很小；满罐工况下罐底的最大等效应力有微量减小。

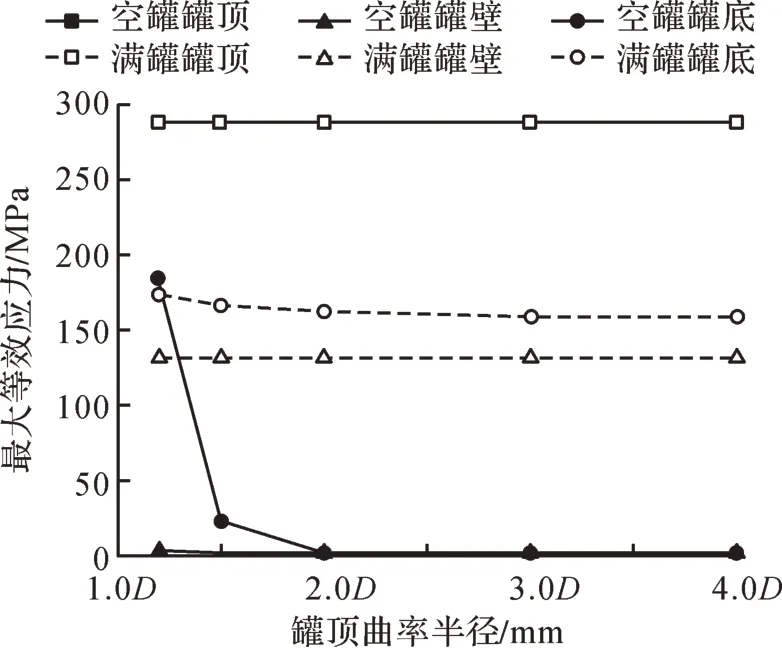
图9 不同罐顶曲率半径下储罐各部件的最大等效应力Fig.9 Maximum equivalent stress of each component of storage tank with different tank roof curvature radiuses

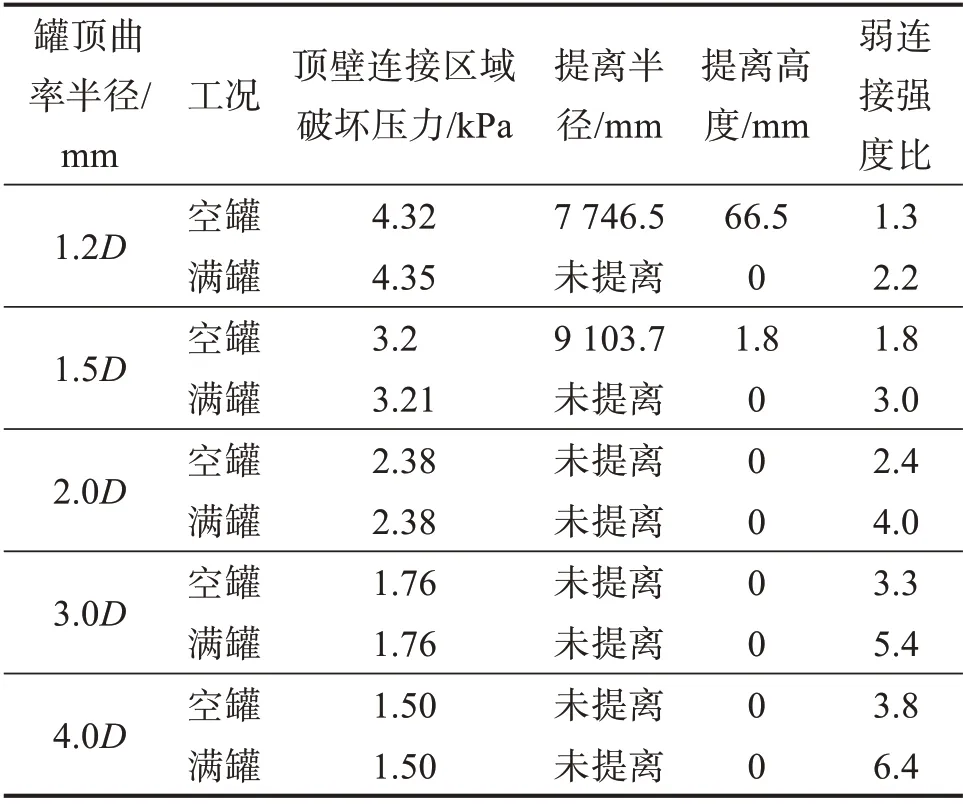
表4 不同罐顶曲率半径下储罐的弱顶性能Table 4 Weak roof performance of storage tank with different tank roof curvature radiuses

由表4可知：随着罐顶曲率半径的增大，顶壁连接区域破坏压力逐渐减小；罐底提离仅在空罐工况下发生，且罐顶曲率半径越大，罐底提离半径越小，而提离高度越大，当罐顶曲率半径达到2.0D后，罐底将不再提离；当罐顶曲率半径达到3.0D后，该储罐将满足GB 50341—2014中弱连接结构储罐的罐顶坡度不大于1/6的要求；各工况下储罐的弱连接强度比随罐顶曲率半径的增大而增大，当罐顶曲率半径增大到3.0D以上时，储罐具备弱顶性能。

综合图9和表4结果可得，适当增大罐顶曲率半径能提升储罐的弱顶性能，使它逐渐满足弱顶结构的设计要求，但这也会降低储罐的承压能力。

4.3 边缘板厚度对弱顶性能的影响分析

取边缘板厚度为11，12，13，14 和15 mm，得到在罐顶破坏压力作用下储罐各部件的最大等效应力随边缘板厚度的变化情况，如图10所示。不同边缘板厚度下储罐的弱顶性能如表5所示。

由图10可知：随着罐底边缘板厚度的增大，罐顶和罐壁的最大等效应力基本不变；空罐工况下罐底的最大等效应力逐渐减小，满罐工况下罐底的最大等效应力先减小后增大，但总体变化幅度均较小。

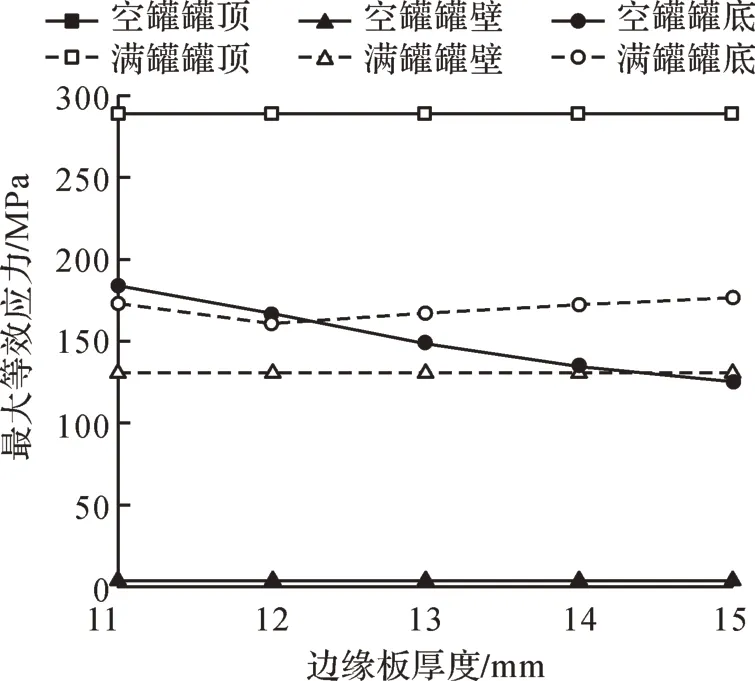
图10 不同边缘板厚度下储罐各部件的最大等效应力Fig.10 Maximum equivalent stress of each component of storage tank with different boundary plate thicknesses

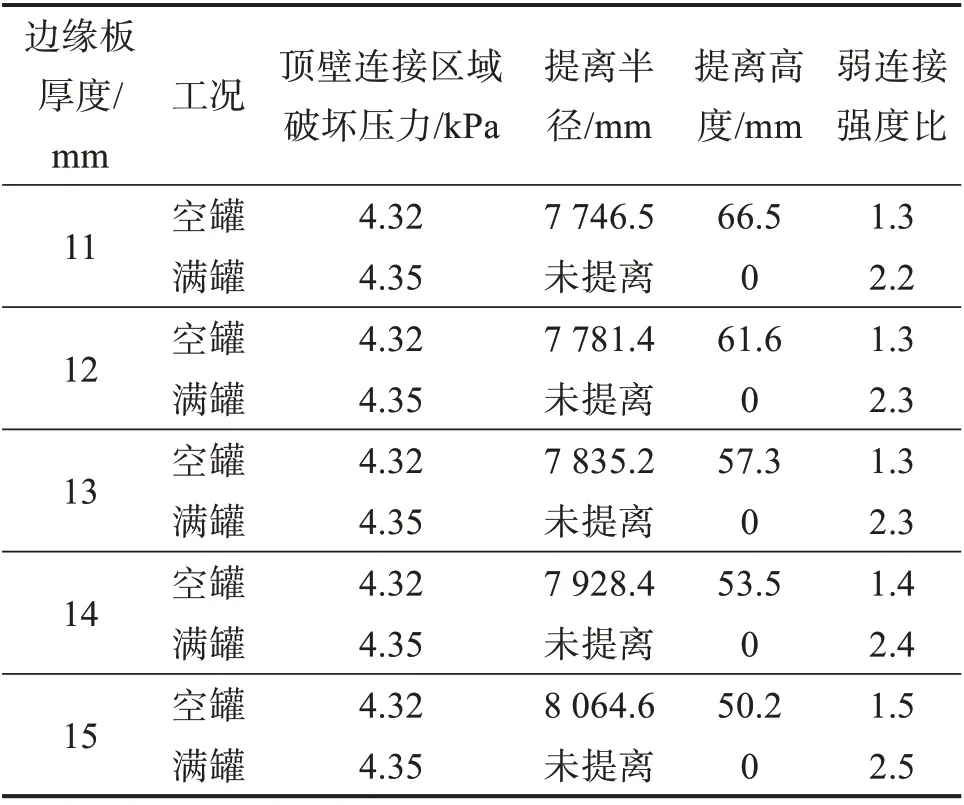
表5 不同边缘板厚度下储罐的弱顶性能Table 5 Weak roof performance of storage tank with different boundary plate thicknesses

由表5可知：随着边缘板厚度的增大，顶壁连接区域破坏压力基本不变；罐底提离仅在空罐工况下发生，且边缘板厚度越大，罐底提离半径越大，而提离高度越小；各工况下储罐的弱连接强度比随边缘板厚度的增大而增大，当边缘板厚度达到15 mm时，储罐具备弱顶性能。

综合图10 和表5 结果可得，适当增大边缘板厚度能提升储罐的弱顶性能，使它满足弱顶结构的设计要求。

4.4 罐体高径比对弱顶性能的影响分析

大型储罐的高径比一般在0.5～2.0之间，因此取高径比为0.5，1.0，1.5，1.78和2.0，得到在罐顶破坏压力作用下储罐各部件的最大等效应力随罐体高径比的变化情况，如图11所示。在不同罐体高径比下储罐的弱顶性能如表6所示。

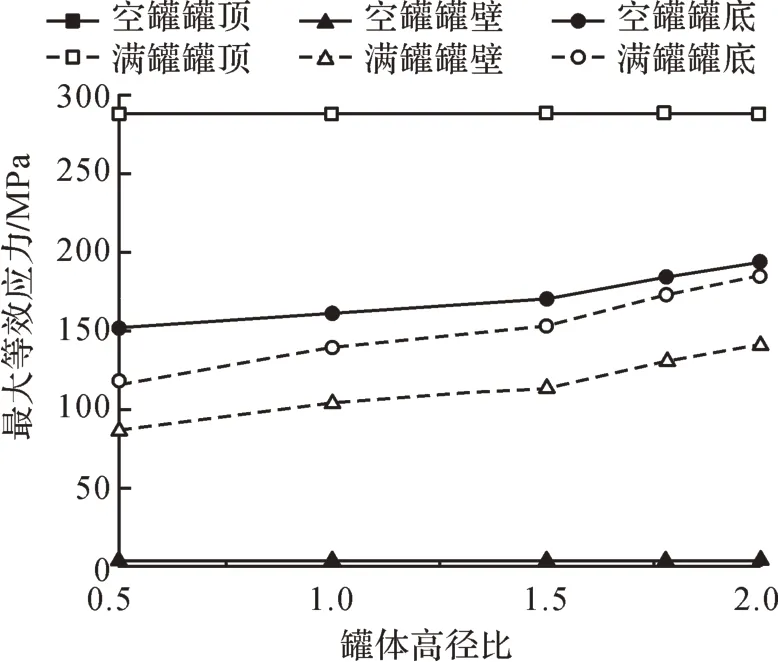
图11 不同罐体高径比下储罐各部件的最大等效应力Fig.11 Maximum equivalent stress of each component of storage tank with different tank height-diameter ratios

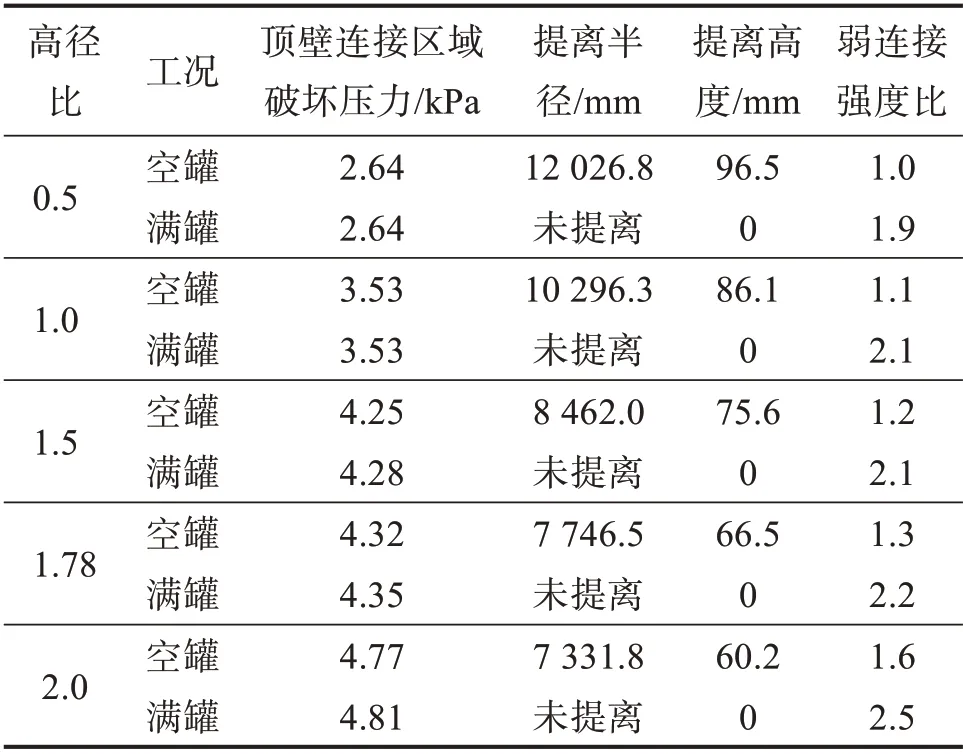
表6 不同罐体高径比下储罐的弱顶性能Table 6 Weak roof performance of storage tank with different tank height-diameter ratios

由图11可知：随着高径比的增大，罐顶最大等效应力基本不变；空罐工况下罐壁的最大等效应力基本不变，但满罐工况下罐壁的最大等效应力逐渐增大，这主要是因为高径比的增大导致相同容量的储液对壁层产生的压力增大；罐底的最大等效应力也逐渐增大。

由表6可知：随着高径比的增大，顶壁连接区域破坏压力逐渐减大，空罐工况下罐底提离高度逐渐减小；各工况下储罐的弱连接强度比随高径比的增大而增大，当高径比达到2.0时，储罐具备弱顶性能。

综合图11 和表6 结果可得，适当增大高径比能提升储罐的弱顶性能，使它满足弱顶结构的设计要求。

4.5 立式拱顶储罐弱顶结构改进

通过以上分析可知，顶壁连接焊角高度、罐顶曲率半径、边缘板厚度和罐体高径比均会对储罐形成弱顶结构产生影响。为使储罐具备弱顶性能并保证储罐的承压能力，可对所设计的拱顶储罐采用适当减小顶壁连接焊角高度、增大罐顶曲率半径、增大边缘板厚度或增大罐体高径比的方法。

5 结 论

1）基于GB 50341—2014设计的5 000 m3立式拱顶储罐的罐顶坡度不满足该标准中弱连接定义的要求，因此该储罐不具备弱顶性能。

2）对基于GB 50341—2014设计的5 000 m3立式拱顶储罐分别进行强度分析与稳定性分析，得到储罐强度破坏压力小于失稳压力，因此储罐先发生强度破坏。

3）对基于GB 50341—2014设计的5 000 m3立式拱顶储罐进行有限元分析，得出它在空罐工况下发生提离，在半罐与满罐工况下不发生提离；各工况下储罐在破坏压力作用下均在罐顶与罐壁连接焊缝处发生破坏，空罐和满罐工况下储罐的弱连接强度比不满足要求，说明该储罐不具备弱顶性能。

4）通过分析储罐结构参数对其弱顶性能的影响，得出将顶壁连接焊角高度减小到3.75 mm，或将罐顶曲率半径增大到3.0D，或将边缘板厚度增加到15 mm，或将储罐高径比增大到2.0，均能使5 000 m3立式拱顶储罐具备弱顶性能。但减小顶壁连接焊角高度和增大罐顶曲率半径会使储罐承压能力下降，而增加边缘板厚度对储罐承压能力影响不大，增大高径比则可提升储罐承压能力，因此在利用上述方法来改进储罐的弱顶性能时，需同时考虑储罐的承压能力。研究结果可为立式拱顶储罐弱顶结构的改进提供一定参考。