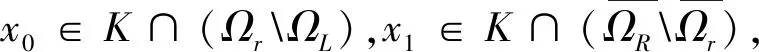带有积分边值的分数阶微分包含正解存在性
2020-05-25杨丹丹张广明
杨丹丹, 张广明
(1.淮阴师范学院 数学科学学院, 江苏 淮安 223300; 2.中国人民解放军32127部队, 辽宁 大连 116100)
0 引言及预备知识
本文主要研究如下分数阶微分包含积分边值问题:
(1)
其中α,β,γ,δ是非负常数,满足ρ=αγ+αδ+βγ>0,Dq表示Caputo分数阶导数,g,h∈C([0,1]×R+),F:[0,1]×R+→ρ(R+)是一个多值映射,ρ(R+)表示 R+的所有非空子集族.
分数阶微分方程是整数阶微分方程的推广[1]. 近年, 分数阶微分方程解的存在性研究有丰富的结果[2-3].2014 年, Yang研究了带有积分边值条件的分数阶微分方程:
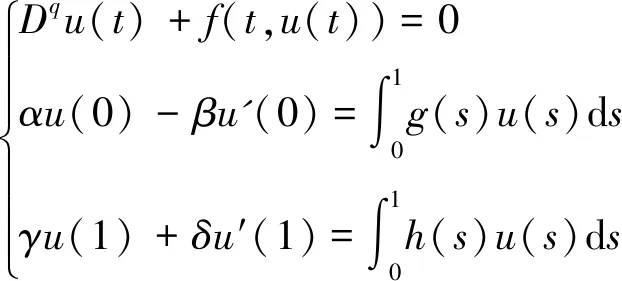
(2)
其中0≤t≤1,1
近年来,关于分数阶微分包含解的存在性研究受到关注[5-9].研究集中在用多值映射的不动点理论,讨论有限维空间和Banach空间中的问题. 现有研究成果中,分数阶微分包含正解存在性定理结果不多[10]. 受参考文[4]启发,本文给出带有积分边值条件分数阶微分包含(1)正解的存在性定理.本文的方法不同于文[5][6][9]并将文[4]的单值研究结果推广到多值情形[1,11-12].
下面给出证明中所用到的定义和引理.
定义1[1]函数u:(0,∞)|→R的α分数阶Caputo导数定义为
其中α>0,Γ是伽玛函数,假设等式右侧在(0,∞)上逐点有定义.
定义2[11]若对于每个x0∈X,集合Θ(x0)是X的一个非空闭子集, 若对于X中的每个包含Θ(x0)开子集B,存在x0的一个开邻域V, 使得Θ(V)⊆B,则称Θ在X是上半连续的.
定义3[3]若Θ是上半连续当且仅当Θ存在一个闭图,即
xn→x*,yn→y*,yn∈Θxn意味着y*∈Θx*.
则称Θ是全连续的.
定义4[12]对于每个y∈C([0,1],R),令SF,y是F的选择集合,定义为
SF,y={f∈L1([0,1],R):f∈F(t,y(t))a.e.t∈[0,1]}.
定义5[11]令 (X,d)是由赋范空间(X,‖·‖)引进的度量空间. 定义度量Hd:ρ(X)×ρ(X)→R∪{∞}如下:
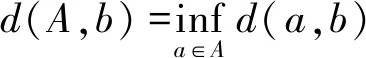
设X为Banach空间,C是X的闭凸子集,CK(C) 表示C中所有非空紧凸子集集合. 对于任意有界子集Ω⊂X,它的非紧测度为γ(Ω)=inf{d>0|Ω可以被有限个直径小于d的集所覆盖}.映射A:G⊂X→X称为k-集压缩(k≥0),若A连续,且满足条件:对每个有界子集Ω⊂G,均有γ(A(Ω))≤k(Ω),对于k<1的k-集压缩称为严格k-集压缩映射. 特别地, 全连续映射是0-集压缩, 因此是严格k-集压缩映射.
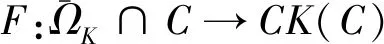
1) 对∀x∈∂EΩr∩C,x∉F(x);
2) 对∀y∈F(x),x∈∂EΩL∩C,有‖y‖>‖x‖;
3) ∀y∈F(x),x∈∂EΩr∩C,有‖y‖≤‖x‖;
4) 对∀y∈F(x),x∈∂EΩR∩C,有‖y‖≤‖x‖;
方便起见, 引入如下记号:
引理2[4]假设D11D12≠1,y∈C([0,1],R),则u(t)是以下问题的唯一一个解
(3)
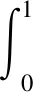
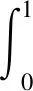
(4)
其中
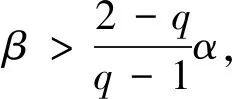
引理4[4]若Q11,Q12∈[0,1),D11D12∈[0,1),β(q-1)>α(2-q),则H(t,s)>0,t,s∈[0,1].λmG(s,s)≤H(t,s)≤MG(s,s),对所有t,s∈[0,1],其中
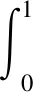
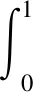
2 主要结果
列出本文的假设条件:
(A1) 多值函数F:[0,1]×R→CK(0,∞);
(A2)F是L1-Caratheodory 且具有非空紧凸值;
(A3) 存在连续非减函数,ψ:[0,∞)→(0,∞)使得‖F(t,x)‖p:sup{|y|:y∈F(t,x)}≤ψ(‖x‖),(t,x)∈(0,1)×R;
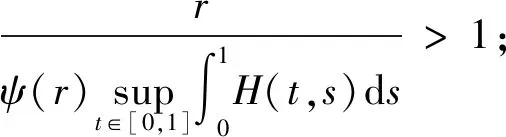
(A5) 存在η∈C[0,1],η>0,有‖F(t,x)‖q:=inf{|y|:y∈F(t,x)}≥η(t)ψ(‖x‖),∀(t,x)∈[0,1]×R;
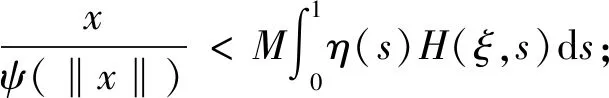
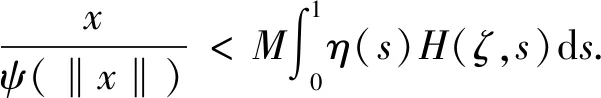
下面,将给出关于分数阶微分包含边值问题(1)正解存在定理.为方便起见,引入以下记号:
定理1 假设(A1)-(A7)成立.则分数阶微分包含积分边值问题(1)至少存在两个正解.
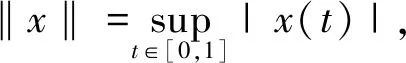
定义
K={u∈C[0,1]:u(t)≥0,t∈[0,1],mint∈[0,1]u(t)≥ω‖u‖},
显然,K是E的一个锥.
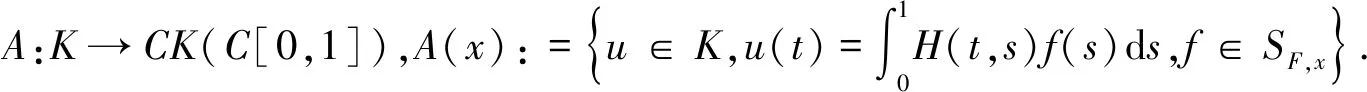
下面只需要证明引理1的所有条件都成立.将证明分为如下五个步骤:
1)A:K→CK(K).∀x∈K,u∈A(x),那么v∈SF,x使得
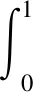
因为F:[0,1]×(0,∞)→CK(0,∞),H(t,s)≥0,有u(t)≥0,t∈[0,1], 由引理4有
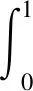
从而∀x∈K,u∈A(x)有u∈K,即A:K→CK(K).
2) ∀y∈∂EΩr∩K,有y∉A(y).
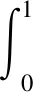
与条件(A4)矛盾.
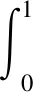
由条件(A4)和(A7),得到
4) ∀u∈A(x),x∈∂EΩr∩K,有
‖u‖≤‖x‖.∀x∈∂EΩr∩K,‖x‖=r,x(t)≥0,t∈[0,1],
即0≤x(t)≤r,t∈[0,1].由ψ非减,由(A3)和(A4)得
5) ∀u∈A(x),x∈∂EΩR∩K,有‖u‖≥‖x‖.任取x∈∂EΩR∩K,则‖x‖=R,mint∈[0,1]x(t)≥ω‖x‖=ωR,故ωR≤x(t)≤R,t∈[0,1],由(A5)和(A7),得