快速反射镜状态模型构建方法及其控制系统设计

艾志伟，嵇建波，李 静，黄书童

快速反射镜状态模型构建方法及其控制系统设计

艾志伟，嵇建波，李 静，黄书童

（桂林航天工业学院，广西 桂林 541004）

为减少快速反射镜状态空间建模过程中所需的结构参数数量，提出了一种基于系统辨识的状态模型构建方法，采用该方法建立状态模型时只需使用音圈电阻和电感两个结构参数。基于状态模型，设计了一套由降阶观测器、状态反馈、内模和镇定补偿器构成的组合控制系统，利用状态反馈完成对内模和镇定补偿器的设计，通过设计降阶观测器实现对电流和角速度的获取，组合系统可同时实现对输入信号的渐进跟踪和干扰的抑制。在SIMULINK中建立仿真模型，仿真结果显示，不考虑干扰作用时，相较于不完全微分PID（Proportion Integration Differentiation）控制系统，组合系统的调节时间下降了53.6%，超调量上升了131.2%；加入干扰信号后，不完全微分PID控制系统的动稳态性能有明显下降，而组合系统的输出性能基本不受影响。仿真结果验证了理论分析的正确性。

快速反射镜；状态模型；渐进跟踪；干扰抑制

0 引言

快速反射镜是一种精密调整光束传播方向的装置，具有结构紧凑、调整精度高、调节速度快的优势[1]，与大惯量的机架共同使用时，可组成粗-精跟踪系统，达到稳定视轴和消除相移的目的，因而被广泛地应用在激光通信[2]、天文望远镜[3]和自适应光学系统的波前校正[4]中。

目前，对快速反射镜系统的研究主要集中在支承结构的设计优化[5]以及控制系统的高精度高带宽设计、扰动抑制[6]等方面。为了提高音圈电机驱动快速反射镜的动态响应特性，中科院长春光机所的王帅[7]提出了一种基于电流环的控制方法，通过为每个音圈电机配置一个高带宽的电流环，实现同一运动轴上的两个音圈电机的同步推拉作用；中科院光电所的邓超、田竟[8-9]在分析建立音圈电机驱动的快速反射镜传递函数模型基础上，设计了基于多种多环路控制的干扰观测器，实现对扰动的抑制；北京航空航天大学的桂潇怡[10]通过在快速反射镜底座中设置两组MEMS加速度传感器测量干扰形成的控制前馈，并采用自适应方法调节前馈环节系数，提高了振动环境下系统的稳定性能。

这些方法在进行系统设计时，使用的被控对象数学模型都是频域传递函数模型，提高控制精度或者进行干扰抑制时，均使用了额外的传感器，多传感器的使用必然增加硬件系统的复杂性。为了在不增加控制系统物理硬件复杂性的基础上得到期望的系统稳态性能和瞬态性能，同时实现对干扰信号的抑制，提出了一种基于系统辨识的状态模型建立方法，该方法在建立状态模型的过程中除辨识出的系统参数外仅用到了音圈电机的线圈电阻和电感，大大减少了建模过程中结构参数的使用，基于状态模型，设计了由降阶观测器、状态反馈、内模和镇定补偿器构成的组合系统，组合系统在不增加额外传感器的基础上实现了多环控制的目的，同时实现了渐进跟踪和干扰抑制的目标。最后，对控制系统进行仿真验证，验证所设计的控制系统的跟踪性能和扰动抑制能力。

1 快速反射镜的状态模型

音圈电机驱动的二自由度快速反射镜具有良好的对称性，为了便于分析，对其中的一个运动轴进行动力学分析，转矩平衡方程为：

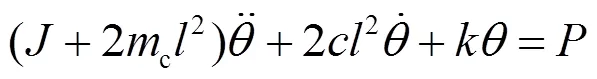
式中：为镜片的转动惯量；为反射镜的输出转角；c为音圈电机线圈的质量；为等效的阻尼系数；为柔性支承结构的转动刚度；为音圈电机作用点到转动中心的距离；是音圈电机作用在运动方向上的力矩，大小为：

＝2f(2)

式中：为通过音圈电机的电流；f是音圈电机力矩系数。

音圈电机为反射镜运动机构提供驱动力矩，根据基尔霍夫电压定律有

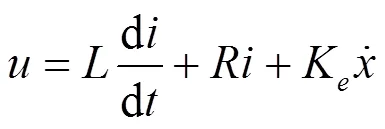
式中：是音圈电机的工作电压；是音圈电机线圈的电感；e是音圈电机的反电动势系数；为音圈电机运动的位移。快速反射镜的运动范围较小，近似有：

≈(4)

联立以上各式，采用古典控制理论的建模方法可知快速反射镜系统数学模型为一个振荡环节和惯性环节组成的三阶线性定常系统，其传递函数可表示为：

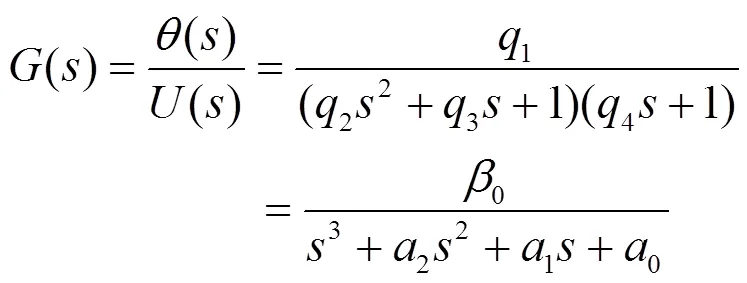
式中：1、2、3、4是待辨识的快速反射镜参数；0、1、2、0是常系数。

根据式(1)、式(2)、式(3)和式(4)，选取负载反射镜的转动角度、角速度、通过音圈电机的电流为系统状态变量，可以得到快速反射镜的状态空间方程：

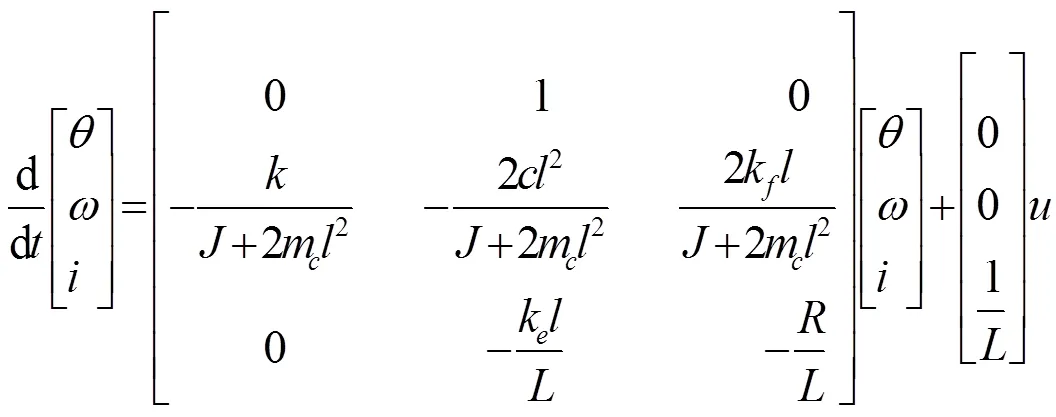
联立式(5)、式(6)有：

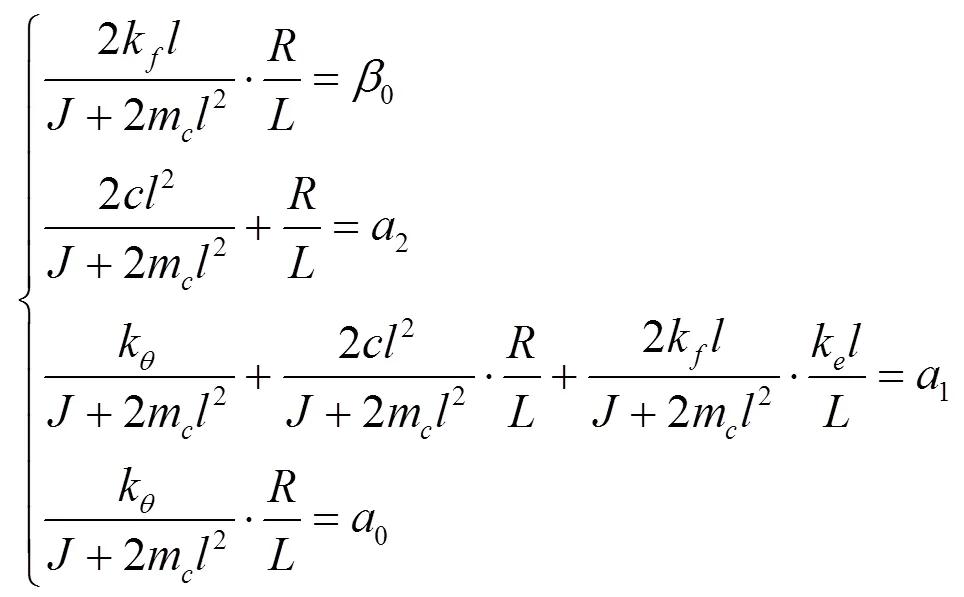
建立快速反射镜的状态空间模型，方法之一是获取到快速反射镜的各个参数，这样状态模型自然可以随之得到，但是由于影响快速反射镜结构参数的量有20个之多，其中很多参数是很难甚至是无法得到，因此采用这种方法建立快速反射镜的状态模型也变得很困难。

通过对式(7)进行分析可知，如果可以通过系统辨识得到快速反射镜传递函数的参数0,1,2,0，那么确定状态模型时只需要得到音圈电机的电阻和电感，使用这6个参量即可完成状态空间模型的搭建。

2 控制系统设计

在经典控制理论中，提高快速反射镜系统的控制精度的普遍的做法是将负载反射镜的位置、速度和加速度或者位置、速度和电流等信号同时进行检测并组成多环控制系统，再为每个环路设计合适的控制器达到提高系统输出精度的目的。工程上，速度、加速度以及电流这些物理量虽然是可以测量的，但是检测装置价格也都比较昂贵，这必然会增加控制系统的成本与增加系统的复杂性。基于快速反射镜的状态模型，可以有效地解决上述问题，通过设计内模、补偿器以及进行状态反馈，同样可以实现多环控制的效果，达到提高控制精度的目的。针对状态反馈过程中难以获取的物理量，可以设计降阶观测器，对状态变量进行估计，然后再将其应用到状态反馈环节中。基于状态模型的组合系统控制框图如图1所示，下面分别对各环节进行参数设计。

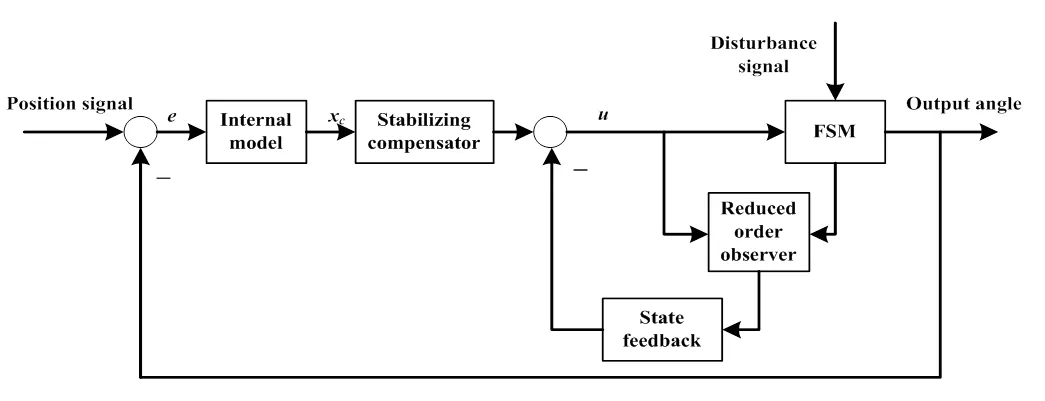
图1 快速反射镜组合控制系统

先将快速反射镜系统方程写成如下形式：

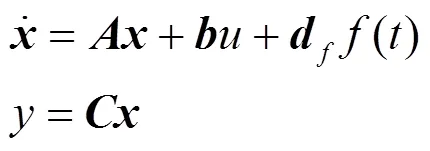
假定系统能控能观，、、分别是对应式(6)的矩阵，()是干扰信号且满足状态方程：

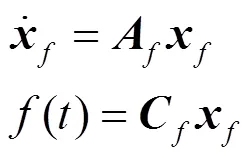
输入信号()由下列方程产生：

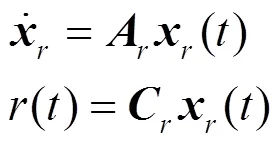
假定上述干扰信号和输入信号均可测量，()和()分别是干扰信号()和输入信号()的特征多项式，即：

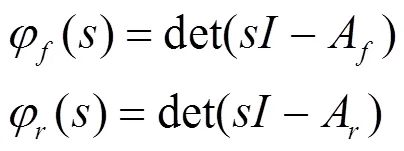
令()为()和()在右半闭平面零点的最小公倍式，则其展开式可以表示如下：

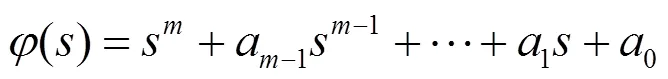
根据内模原理，内模－1()的状态空间模型可实现为：

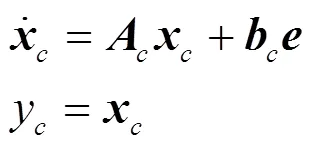
在不考虑干扰信号时，误差信号＝－，可得内模状态方程为：

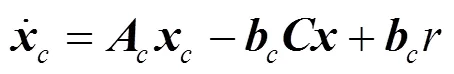
快速反射镜系统与内模串联组成的系统状态方程为：

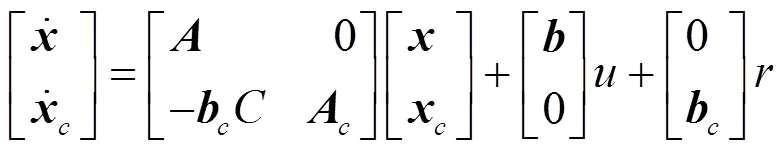
假设组合系统能控，引入状态反馈控制c和镇定补偿器，控制输出为：

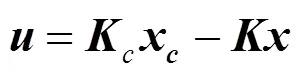
引入状态反馈后的组合系统的状态方程为：

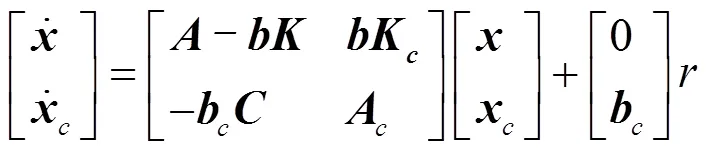
下面继续对受控快速反射镜系统进行研究。系统输出是反射镜的转角，将这个状态变量用1表示。组合系统需要使用的是转角，角速度和电流3个状态变量，因为转角已知，要得到全部3个状态变量，只需要构造一个低阶的观测器估计剩余的2个状态即可，这2个状态变量用2表示，据此，可将受控快速反射镜系统的状态空间模型写成如下形式：

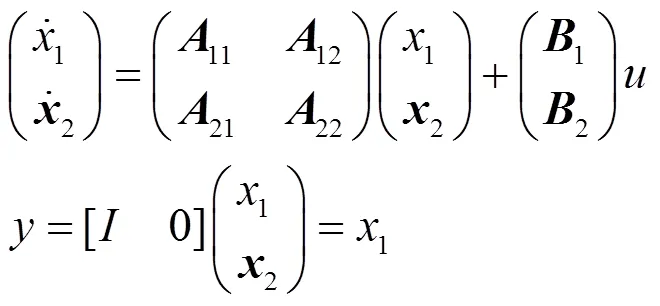
对上式进行展开，有：

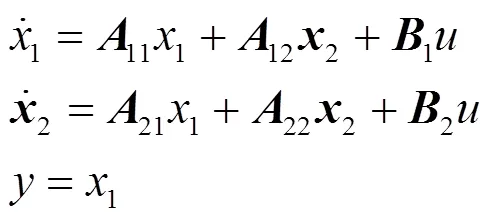
下面对不能测量得到的电流和角速度两个状态变量设计观测器进行观测，令：

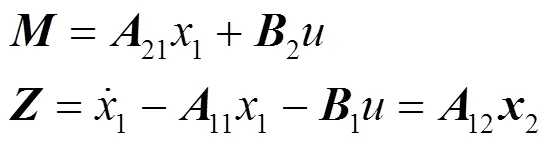
则上式可以变成：

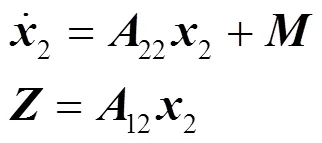
如果将视为系统输入量，视为输出量，22和12分别视作系统矩阵和输出矩阵，则上式可以看成是受控快速反射镜系统的一个子系统，2个状态变量均不能直接量测得到，为此可以通过构建一个2维的状态观测器，实现对这2个状态的重构，状态不可量测子系统的状态观测器为：

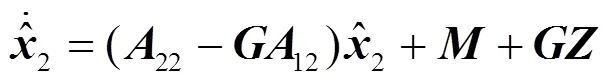
为了在原系统中可以实现该状态观测器，需要消去中间变量，，将式(20)带入式(22)，可得：

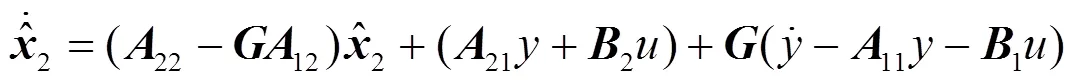
工程中的信号通常包含有大量的噪声，在系统中直接对输出信号进行微分会在控制系统引入噪声干扰，为避免微分运算，引入中间变量，令：

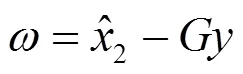
对变量进行求导，经整理可得：

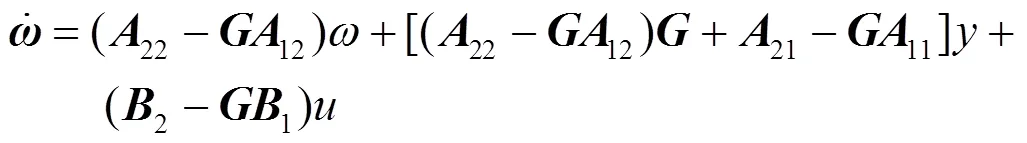
降阶观测器得到系统状态变量为：

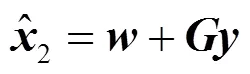
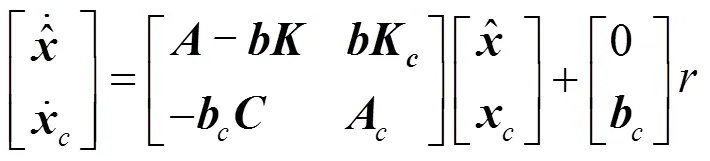
根据快速反射镜控制系统的性能指标要求，确定出控制系统闭环主导极点的位置，保证另一极点的实部比主导极点的实部大3～6倍以上时可忽略该极点对控制系统输出性能的影响。降阶观测器的特征根应该有比状态反馈系统特征根更大的实部模。

由闭环系统主导极点确定的特征方程式和组合系统的特征方程式相等，即可确定反馈环节和镇定补偿器的参数。

3 仿真实验与结果分析

对一款工程中使用的快速反射镜进行了系统辨识，通过拟合得到的快速反射镜开环模型为：

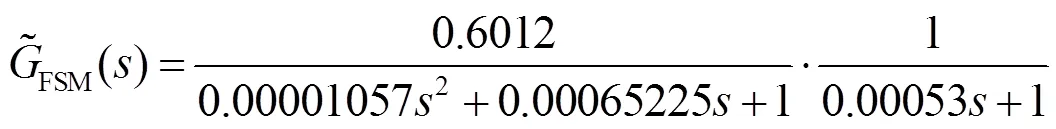
音圈电机的标称电感和电阻分别为1.9mH和3.6W，得到快速反射镜的状态方程为：

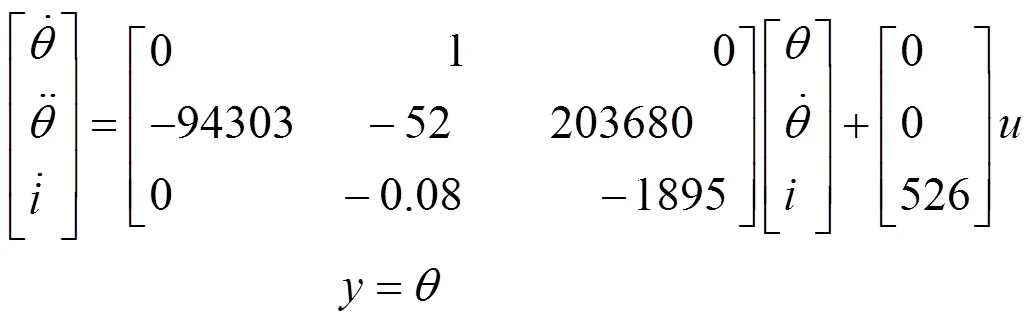
采用扫频法辨识出的快速反射镜开环系统模型、拟合得到的系统模型以及状态模型幅频特性曲线对比图如图2所示，从图中可以看到状态模型与辨识出的系统曲线基本重合。

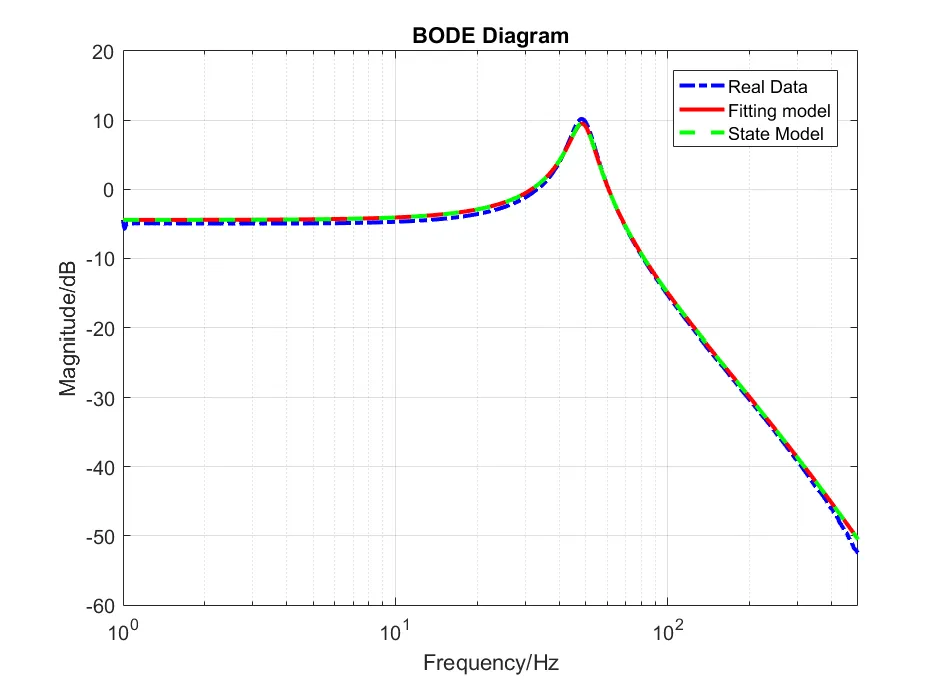
图2 幅频特性曲线对比图

对于系统来说，阶跃信号是最具挑战性的，故选择单位阶跃信号()＝1()作为系统测试输入，扰动信号选为正弦信号()＝sin()，可得()＝3＋，内模可实现为：

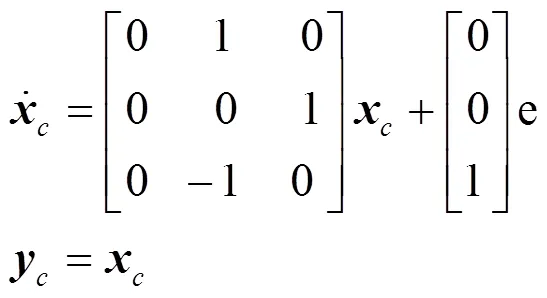
给定快速反射镜闭环控制系统的设计指标是：超调量小于10%，调节时间小于10ms。通过配置状态反馈环节的参数将系统的极点配置在复平面希望位置上，结合主导极点的定义，可将系统的预期的主导极点取为1,2＝－440±j448，其他极点为：

3,4＝－2000±j1000，4,5＝－3000±j1500

计算并对参数修正后得状态反馈环节和镇定补偿器分别为：

＝[1057.9, 0.4552, 16.9829]

c＝[2.2303, 7.3806×106, 1.2892×106]

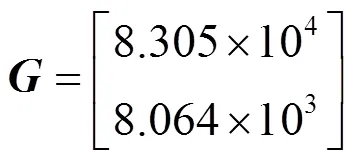
由于采用改进根轨迹的方法设计不完全微分PID控制系统的参数时，也是以时域性能指标要求为设计出发点，因此选择以同样性能指标要求时采用该种方法确定的控制系统作为对照实验系统。不考虑扰动信号作用时，两种方法的系统输出曲线如图3所示。从图中可以得到，不完全微分PID控制系统的峰值时间为0.0070s，调节时间为0.0049s，超调量为4.0195%，而组合系统的峰值时间为0.0019s，调节时间为0.0023s，超调量为9.2950%，相较于不完全微分PID控制系统，组合系统的峰值时间下降了72.85%，调节时间下降了53.06%，超调量则上升了131.2%，组合系统的超调量虽有所上升，但仍然满足性能指标的要求。

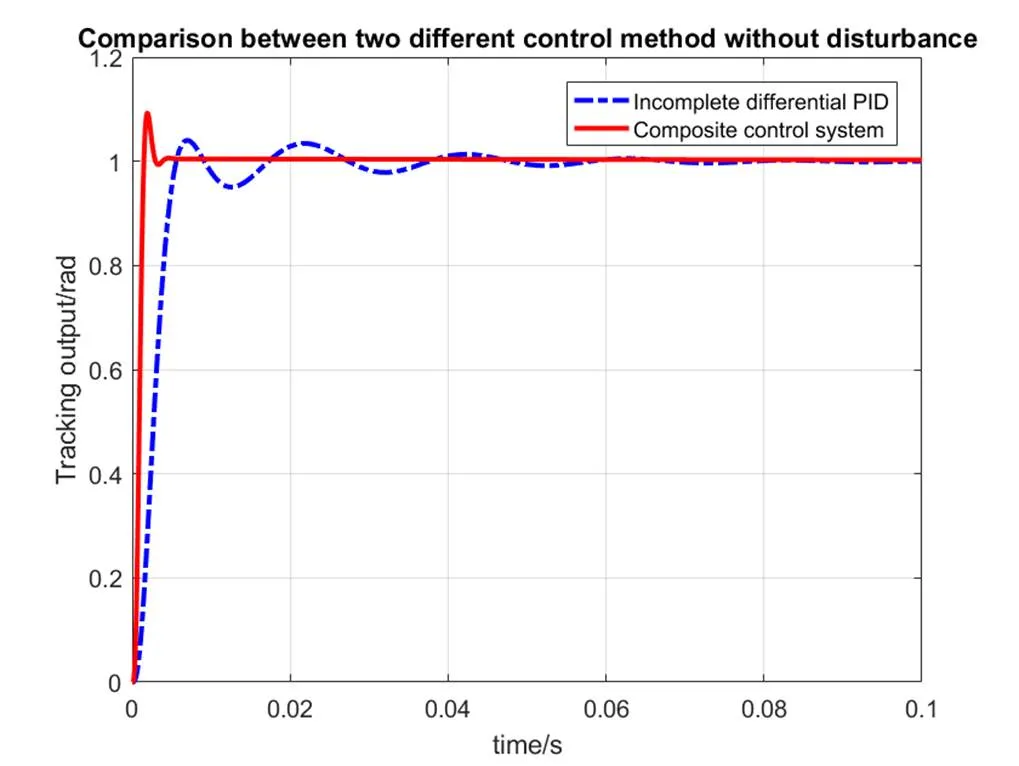
图3 不考虑干扰时两种控制方法输出曲线

在系统中施加幅值为1，圆频率为100rad/s的正弦干扰信号前后不完全微分PID控制系统的输出曲线如图4所示。从图中可以看到，施加扰动作用后系统输出会在平衡点上下震荡，影响了控制系统的稳态精度。

加入同样的扰动后，组合系统的输出曲线如图5所示，从图中可以看出，加入干扰信号作用后组合系统的峰值时间为0.0019s，调节时间为0.0023s，超调量为9.2950%，加入干扰信号前后，组合系统的输出曲线基本重合，峰值时间、调节时间和超调量等时域性能指标也完全一样。仿真结果证明了基于状态反馈的组合系统可以同时实现对输入的渐进跟踪和对干扰信号的抑制。

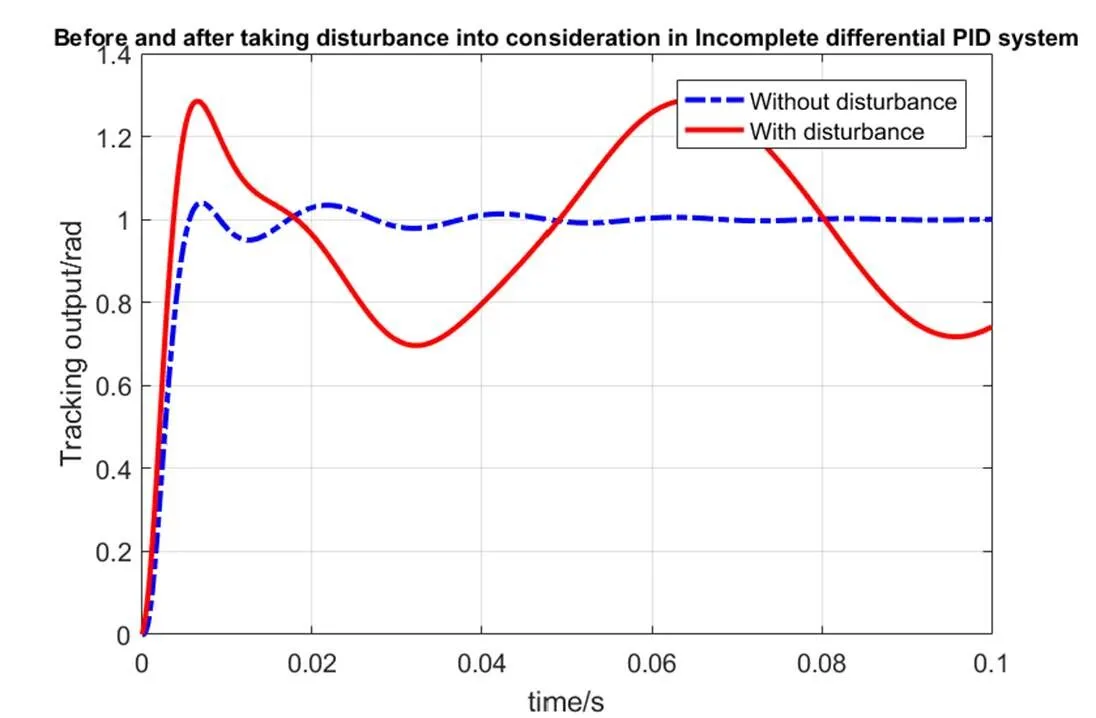
图4 幅值为1频率为100rad/s的干扰作用前后不完全微分系统输出曲线对比

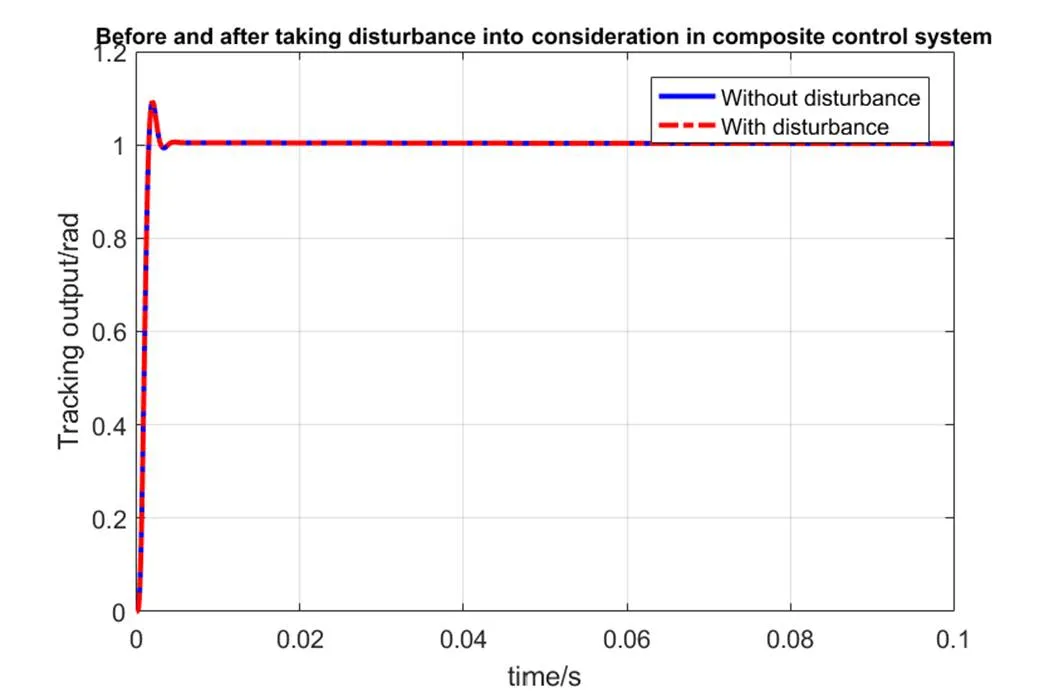
图5 幅值为1频率为100rad/s的干扰作用前后组合系统输出曲线对比

加大干扰信号作用，在系统中施加幅值为10，圆频率为1000rad/s的正弦干扰信号，加入干扰信号前后，不完全微分PID控制系统的输出曲线和组合系统的输出曲线分别如图6和图7所示。从图6中可以看到，加大干扰信号作用后，不完全微分PID控制系统的输出完全失真；从图7中可以看到，加大干扰信号作用后，组合系统的峰值时间为0.0019s，调节时间为0.0023s，超调量为9.4326%，可以发现组合系统受干扰信号的影响很小。通过对比图5和图7还可以发现组合系统对扰动信号的频率也具有较低的灵敏度，这是由于在进行组合系统设计过程中用内模抵消了干扰信号的作用，实现了组合系统对扰动的全频段抑制，与理论期待相符。

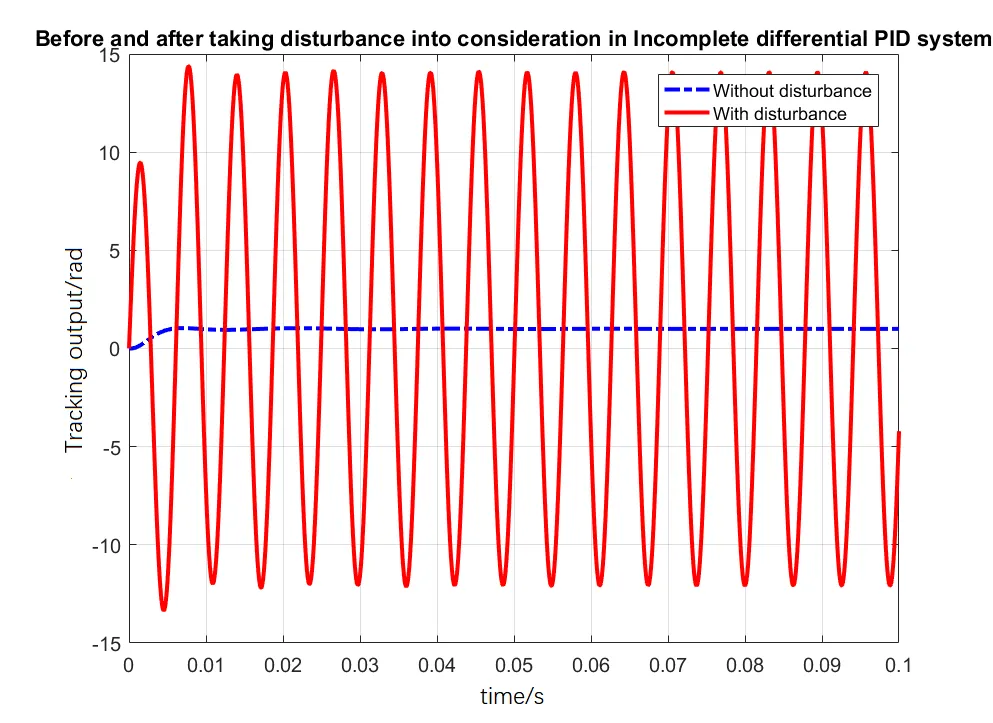
图6 幅值为10频率为1000rad/s的干扰作用前后不完全微分系统输出曲线对比

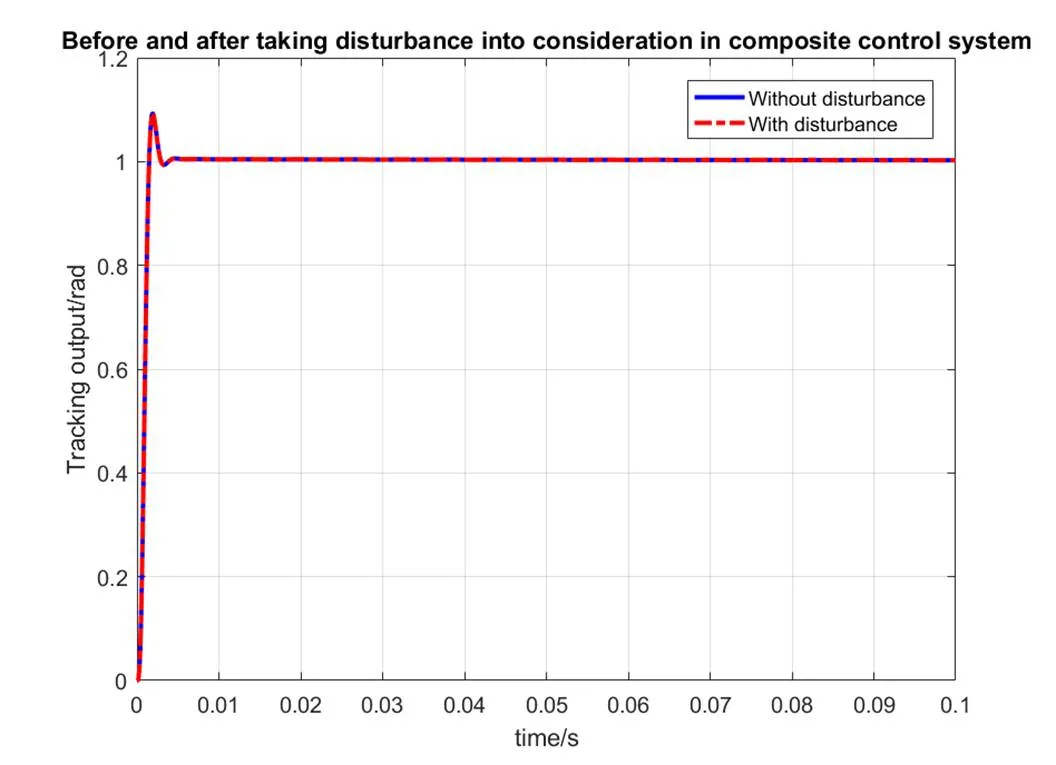
图7 幅值为10频率为1000rad/s的干扰作用前后组合系统输出曲线对比

4 结论

为使得设计的控制系统可以同时实现对输入信号的渐进跟踪和对可测干扰信号的抑制，亦不增加控制系统硬件复杂程度，本文从状态模型的快速建立为出发点，提出一种基于系统辨识的状态模型建立方法，该方法只需要使用6个参量即可完成状态模型的建立，大大减少了建模过程中结构参数的使用。基于快速反射镜的状态模型，设计了一套组合控制系统，并着重分析了组合系统中内模、状态反馈和镇定补偿器的设计方法，给出了组合系统中降阶观测器实现方法，分析计算出组合系统状态方程。对工程上使用的一款快速反射镜应用了上述组合控制系统，给出了控制系统的具体参数，并进行了仿真验证，仿真结果表明理论分析的正确性。

[1] Kluk D J, Boulet M T, Trumper D L. A high-bandwidth, high-precision, two-axis steering mirror with moving iron actuator[J]., 2012, 22: 257-270.

[2] 赵磊, 纪明, 赵振海, 等. 舰载激光武器稳定平台粗精复合控制[J]. 激光与红外, 2019, 49(1): 86-92.

ZHAO Lei, JI Ming, ZHAO Zhenhai, et, al. Primary-precise compounded control for stabilized platform in shipborne laser weapon[J]., 2019, 49(1): 86-92.

[3] 吕世良, 刘金国, 周怀得, 等. 星载红外探测器快速反射镜控制系统设计[J]. 红外与激光工程, 2017, 46(9): 102-107.

LYU Shiliang, LIU Jinguo, ZHOU Huaide, et al. Design of control system for fast steering mirror of infrared detector based on satellite[J]., 2017, 46(9): 102-107.

[4] WANG Kaidi, SU Xiuqin, LI Zhe, et al. Time-frequency characteristics optimal control of fast steering mirror for image motion compensation[J]., 2018, 47(S1): 120-126.

[5] 鲁亚飞, 范大鹏, 范世珣, 等. 快速反射镜两轴柔性支承设计[J]. 光学精密工程, 2010, 18(12): 2574-2582.

LU Yafei, FAN Dapeng, FAN Shixun, et, al. Design of two-axis elastic support for fast steering mirror[J]., 2010, 18(12): 2574-2582.

[6] 彭树萍, 于洪君, 王伟国, 等. 新型快速反射镜伺服系统设计[J]. 红外与激光工程, 2014, 43(5): 1610-1615.

PENG Shuping, YU Hongjun, WANG Weiguo, et al. Design of servo system for novel fast-steering mirror[J]., 2014, 43(5): 1610-1615.

[7] 王帅, 曹玉岩. 音圈电机型快速反射镜的驱动控制系统设计[J]. 电子测量与仪器学报, 2017, 31(7): 1115-1121.

WANG Shuai, CAO Yuyan. Design of control system for fast steering mirror driven by voice coil actuator[J]., 2017, 31(7): 1115 - 1121.

[8] DENG Chao, TANG Tao, MAO Yao, et al. Enhanced disturbance observer based on acceleration measurement for fast steering mirror system[J]., 2017, 9(3): 1-11.

[9] TIAN Jing, YANG Wenshu, PENG Zhenming. Application of MEMS Accelerometers and Gyroscopes in Fast Steering Mirror Control Systems[J]., 2016, 440: 1-13.

[10] 桂潇怡, 李伟鹏, 郑新涛, 等. 基于MEMS加速度计的快速反射镜复合控制[J]. 航天控制, 2018, 36(2): 30-36, 41.

GUI Xiaoyi, LI Weipeng, ZHENG Xintao, et al. Composite Control of Fast Steering Mirror Based on MEMS Accelerometer[J]., 2018, 36(2): 30-36, 41.

State Model Construction Method for Fast Steering Mirror and Its Control System Design

AI Zhiwei，JI Jianbo，LI Jing，HUANG Shutong

(Guilin University of Aerospace Technology, Guilin 541004, China)

To reduce structural parameters needed in the process of the state space modeling of a fast steering mirror (FSM), a modeling method based on system identification is proposed. Only two structural parameters, namely, coil resistance and inductance, are needed when using this modeling method. Based on the state model, a set of combined control systems consisting of a reduced-order observer, state feedback, an internal model, and a stabilization compensator were designed; the internal model and stabilization compensator were designed by using state feedback. Furthermore, current and angular velocity can be obtained using a reduced-order observer. The combined system can progressively track of input signals and suppress disturbances; the simulation model was built using SIMULINK. The simulation results show that, compared with the incomplete differential proportional integral derivative (PID) control system, the setting time decreases by 53.6% and the overshoot increases by 131.2% without considering the disturbance in the composite system. The dynamic and steady-state performance of the incomplete differential PID control system decreases significantly after adding the disturbance signal, while the composite system is maintained. The simulation results verify the correctness of the theoretical analysis.

fast steering mirror, state model, progressive tracking, disturbance suppression

TP273

A

1001-8891(2020)01-0040-06

2019-07-09；

2019-12-31.

艾志伟（1992-），男，硕士，助教，主要研究方向为光电跟踪控制。E-mail：aizhiwei752@163.com。

广西高校中青年教师科研基础能力提升项目（2019KY0793）。