压裂工况下T形三通冲蚀影响数值模拟

刘洪亮，李美求，潘 力，江宇潇

(1.长江大学机械结构强度与振动研究所，荆州 434023;2.中石化四机石油机械有限公司，荆州 434023)

非常规油气[1-3]资源开采广泛用到大型压裂设备，压裂管汇是整个压裂系统的血脉，酸化压裂中盐酸[4-5]对压裂管汇内壁有腐蚀作用，支撑剂对管壁有冲蚀作用，冲蚀和腐蚀的协同作用使得管壁质量减薄更加严重，显著降低管道内部临界载荷[6]。三通是压裂装备的重要组成部分，高速携砂液在三通处流场发生急剧变化，使得三通存在严重的冲蚀现象。目前，压裂管道壁厚的检测主要是拆下后进行测量，三通冲蚀研究意义重大。目前对于此类三通的研究不是很多，张继信等[7]进行了T形三通冲蚀数值模拟，得出进出口方式不同改变了管汇冲蚀区域，腋窝及肩部是T形三通冲蚀最严重的区域。张孟昀等[8]进行90°弯管与90°盲管的对比冲蚀数值模拟，得出参数都大致相同的状况下，盲管的冲蚀率比弯管要小得多。王国荣等[9]进行了40Cr的冲蚀实验，表明当颗粒冲击靶材角度由15°增大至90°时，冲蚀坑的形貌渐渐脱离椭圆状，并且渐渐发展成为圆形，冲蚀的深度增大后减小，在冲击靶材角度45°时取得极大值。陈宇等[10]对连接结构尺寸不同的三通进行数值模拟，得出连接结构不改变三通的冲蚀区域，二者的冲蚀情况基本相似，球体三通抗冲蚀能力高于T形三通；流道变化处球头的半径为三通直径的2倍时抗冲蚀能力最强。易先中等[11]通过进行弯管Fluent在压裂工况下的冲蚀数值仿真模拟，得出流速是造成冲蚀破坏的主要因素。目前压裂T形三通的冲蚀规律的研究有待完善，本文以T形三通为研究对象进行数值模拟，重点分析压裂工况对其的影响。

1 T形三通物理模型

以某石油机械厂生产的压裂作业中常用的T形三通作为研究对象，该三通内径为70 mm，外径为104 mm。建模时设置三通各段的长度为内径的5倍，使流体在冲蚀管道前得到充分发展。在Solidworks中建立压裂T形三通零件实体模型，T形三通的结构示意图如图1所示,参数如表1所示。通过ICEM绘制流道六面体结构化网格，网格数量为163 498个，平均网格质量为0.89。

图1 T形三通管模型

表1 T形三通管详细参数

2 压裂T形三通数值分析模型

Fluent中内置的离散相模型(DPM)进行冲蚀仿真要求固体粒子的体积分数小于6%，适当的设置参数使得压裂液中的支撑剂占总体积分数的不超过6%，这样压裂液对压裂管道的冲蚀可以用Fluent中内置的离散相模型来进行仿真。周兆明等[12]的实验也证明了Fluent软件中的离散相模型可以用来计算压裂液对管道的冲蚀。

2.1 支撑剂及连续相介质

压裂施工现场实际使用支撑剂以人造陶粒为主，且支撑剂颗粒形状相对来说很规则，可以简化为球形，支撑剂密度为2 750 kg/m3，体积密度为1 800 kg/m3，支撑剂铝矾土粒子直径为70 μm，携砂液介质为清水，为不可压缩流体。

2.2 离散相颗粒轨道计算模型

离散相模型不考虑支撑剂粒子对支撑剂粒子的作用。笛卡尔坐标下颗粒的运动方程[13]为

(1)

式(1)中：up表示颗粒速度，m/s；u表示携砂液速度，m/s；FD(u-up)表示固体颗粒受到的力；gx表示重力在x方向的分量，m/s2；ρ表示压裂液的密度，kg/m3；ρp表示粒子的密度，kg/m3；Fx表示单位质量颗粒在x方向受的其他力。

2.3 冲蚀率

Fluent液固两相流管道冲蚀包括的参数有冲击角函数、相对速度参数、冲蚀面积等，冲蚀率定义为单位时间和面积下金属材料损失的质量。冲蚀率[14]表示为

(2)

式(2)中：R表示冲蚀率，kg/(m2·s)；N表示颗粒数目；mq表示支撑剂质量流量，kg/s；C(dp)表示颗粒直径的函数，常取1.8×10-9；α为颗粒撞击壁面的撞击；f(α)表示冲击角的函数，参照张孟昀等[8]取值；b(v)为相对速度的系数，取为2.6；A为壁面单元面积，m2。

2.4 内置的湍流模型

压裂管汇内部流场变化复杂，湍流的各向异性使得标准К-ε模型产生计算误差。RNG К-ε模型相比标准К-ε模型，主要针对旋涡、壁面弯曲率过高或流动轨迹过于弯曲等场合，因此采用RNG К-ε模型。

2.5 壁面碰撞恢复系数

运动中的颗粒撞击压裂管道内壁，产生能量交换，造成能量消耗，改变了颗粒的运动方向及大小改变，能量损失情况用恢复系数描述。采用Grant等[15]恢复系数，切向与法向系数方程为

(3)

3 计算结果与分析

3.1 流速对压裂T形三通冲蚀的影响

将入口速度设置首项5 m/s，末项30 m/s，公差是5 m/s的等差数列，不改变其他参量数值。由Fluent仿真得到的最大冲蚀率数值如图2所示。

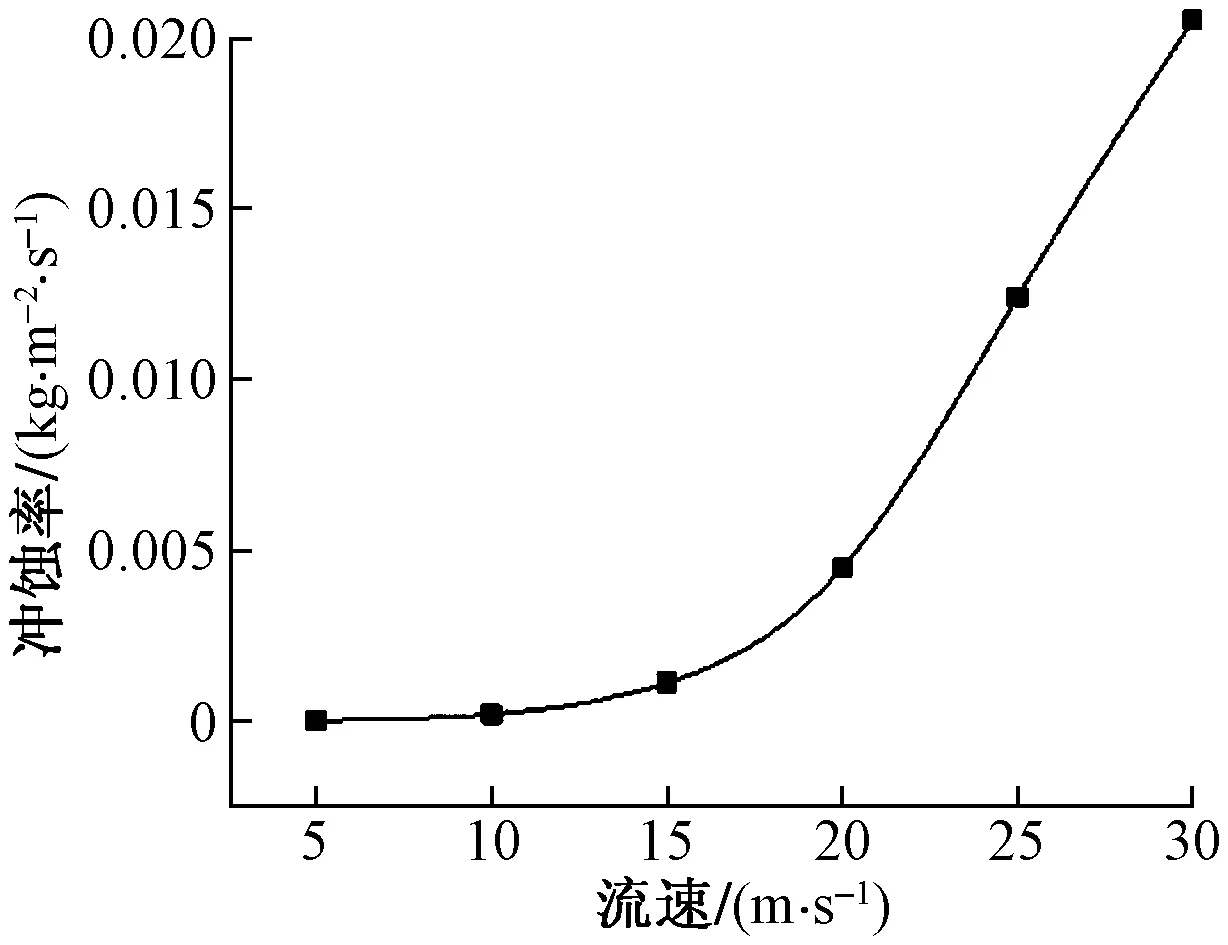
图2 最大冲蚀率随流速变化关系

由图2看出，流速与冲蚀率的变化关系呈现幂函数关系，液体速度对T形三通冲蚀率的影响曲线中存在临界流速，当液体流速小于临界流速，流速的增加引起冲蚀程度增加较不明显，当流速超过临界流速，流速的轻微增加，引起冲蚀率的急剧增加。

3.2 颗粒直径对压裂T形三通冲蚀的影响

将入口质量流量设置为70目为首项，20目为末项，公差为10目的等差数列，不改变其他参量的数值。由Fluent仿真得到的最大冲蚀率数值如图3所示。

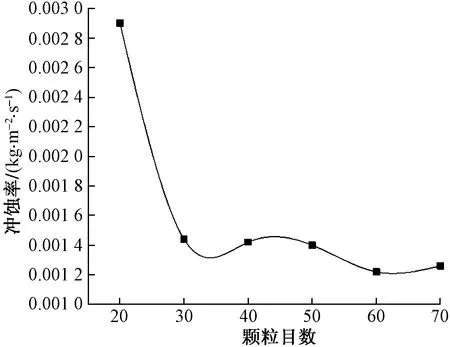
图3 最大冲蚀速率随颗粒大小的变化关系

由图3可以看出，支撑剂颗粒粒径与冲蚀率的变化关系呈正相关，在使用某种携砂液时，对于不同支撑剂，它们的最佳颗粒粒径各不相同，且此时的颗粒对壁面的冲击最小。

3.3 流向变化对压裂T形三通冲蚀的影响

将压裂T形三通分为三种不同的类型：分流型、汇流型、既不分流也不汇流型。A、B、C表示三通的三个进出口，I、O表示进、出状态，压裂T形三通可能的进出口使用情况如表2所示。

表2 不同组进出口流通状态

因有些组数仅仅是进出口调换，冲蚀结果完全相同，所以表2列出了不重复的所有情况。按照3.2节介绍的冲蚀仿真参数在Fluent软件中进行设置，仅仅是改变压裂管T形三通管件的进出流通状态，保持其他参数的值不变。由Fluent数值模拟所得出冲蚀率结果云图如图4所示。

压裂T形三通进出口流通状态改变的同时，也造成了管道内壁易冲蚀区域的变化。压裂T形三通相贯线区域及流道交互区相连接的三个直管区域附近最易发生冲蚀现象。

a组的冲蚀率是b组、d组的3倍，产生这三种冲蚀区域及冲蚀率差异的原因在于：一是a组液体在T形三通管件流道交汇处没有分流。二是b组液体水平流出，仅仅在相贯线处，有部分颗粒撞击相贯线。三是d组的液体在流道交汇一分为二。

b组与d组冲蚀率大致相同，产生这两种冲蚀区域差异的原因在于：一是d组液体形成了严重的低角度冲刷，且在水平直管端进行了分流；二是因为d组液体水平流出，有部分颗粒撞击相贯线，而且此时颗粒撞击壁面的速度是d组速度的0.5倍。

c组的冲蚀率是第8组的0.5倍，产生这两种冲蚀区域及冲蚀率差异的原因在于：一是因为在c组中液体对管壁的冲击角度比较小，形成了严重的低角度冲刷；二是d组液体在流道变化处进行了分流，走水平直管流出的液体造成的冲蚀较小。

e组的冲蚀率是f组的1.75倍，产生这两种冲蚀区域及冲蚀率差异的原因在于：在f组状况下，液体从水平直两管端口进入，恰好在流体交互区域有部分液体的动能受到了抵消。

汇流状态下的冲蚀率最大，分流状态下的冲蚀率最小。汇流状态下的冲蚀率最大可以是分流状态下的30.7倍；既不分流也不汇流状态下的最大冲蚀率可以达到了分流状态的冲蚀率的5.4倍。流通方式变化会对冲蚀位置产生影响，冲蚀区域主要集中在相贯线区域及流道交互区相连接的三个直管区域。可以利用其冲蚀规律，将冲蚀严重的压裂T形三通更换到冲蚀位置不同或冲蚀速率较小的地方，有效延长T形三通管件的使用寿命。

图4 不同进出口状态的冲蚀结果云图

4 结论

(1)压裂T形三通内部流速与冲蚀率的变化关系呈现幂函数关系，且曲线中存在冲蚀影响临界流速。当液体流速小于临界流速，流速的增加引起冲蚀程度增加较不明显，当流速超过临界流速，流速的轻微增加，引起冲蚀率的急剧增加。

(2)支撑剂颗粒粒径与冲蚀率的变化正相关，在使用某种携砂液时，对于不同支撑剂，它们的最佳颗粒粒径各不相同，且此时的颗粒粒径对壁面的冲击最小。

(3)汇流状态下的冲蚀率最大，分流状态下的冲蚀率最小。汇流状态下的冲蚀率最大可以是分流状态下的30.7倍；既不分流也不汇流状态下的最大冲蚀率可达到分流状态的冲蚀率的5.4倍。流通方式变化会对冲蚀位置产生影响，冲蚀区域主要集中在相贯线区域及流道交互区相连接的三个直管区域，可以利用其冲蚀规律，将冲蚀严重的压裂T形三通更换到冲蚀位置不同或冲蚀速率较小的地方，有效地延长T形三通管件的服役时间。