固结蠕变下软土微观结构参数的定量分析

陈建平，袁 杰，叶辽羽，彭秋旺

(广州大学土木工程学院，广州 510006)

通常来说，土体的微观结构包括土体颗粒的形状、大小、排列及连接关系和孔隙的分布特性[1]，土体微观结构的变化能够影响宏观物理学性质，宏观特性是微观结构的一个外在体现。从20世纪20年代起，不断有国外学者提出软黏土微观结构的概念。塔萨奇等[2]进行了土体微观结构的研究，认为土体微观结构是蜂窝状的，是最先对土体微观结构进行探究的科研工作者。Casagranda[3]基于塔萨奇的研究成果，对土的蜂窝状结构进行更深层次的探究。陈宗基[4]对黏土蠕变特性进行定性的描述，提出黏土中片状颗粒有三种接触形式：点-面接触、边-面接触、面-面接触，用三维网络模型来反映粘土片状颗粒的相互作用。张先伟等[5]利用扫描电镜对中山、广州和青岛的原状软土进行扫描，基于像素和灰度的变换关系，从SEM图片中获取软土的三维微观数据，用三维软件把二维平面的微观结构表面转换成三维可视的立体图形。周晖等[6]对珠三角典型的软土进行单向压缩试验，利用环境扫描电子显微镜(ESEM)所得的照片研究软土在不同固结压力条件下的微结构大小、形状、定向性等微结构参数，分析其变化规律。

虽然现在对软土的力学性能研究比较充足，但从微观上分析还较为匮乏，探究土的微观结构特性能够更加准确地描述土的变形过程。通过微观试验分析土的微观结构，从本质上分析出番禺软土的固结蠕变变形机理，研究土体的微观结构可以解释土的宏观现象，土体的结构特性复杂。

1 试样制备及步骤

试样用仪器为日本电子热场发射扫描电镜，通过扫描电镜可以测得样品的表面形貌和结构特征[7]。试验步骤如下：

(1)试样制备：将采用细钢丝将固结蠕变前后的土样切成长约20 mm、宽约15 mm、高约20 mm的长条形土样，分别在土样的水平方向和垂直方向的中部刻一条5 mm的小凹槽，以便于试验时获取不同方向的新鲜结构面。使用真空冷冻干燥仪器进行试样制备，可以使蠕变前后的试样基本不扰动，达到既干燥又不变形的目的[8]。将制备好的长条形土样先放在-196 ℃液氮中迅速冷冻1 h，然后在-50 ℃状态下用冷干机抽真空24 h。

(2)试样固定：将经过冷冻真空干燥法制得的干燥土样从小凹槽处小心地掰开，用吹气球把断面上细小的颗粒吹走，获得新鲜的结构面，通过导电胶固定在金属托盘上。

(3)试样镀膜：将试样放进真空离子溅射仪，在试样表面充分镀一层金膜，以使其表层具有良好的导电性，能避免试样在拍摄过程中产生的放电现象。

(4)试样扫描：将镀好膜的试样放进扫描电镜的样品室进行扫描，扫描时先从高倍发现典型的土体颗粒和孔隙，在逐渐地降低放大倍数，以保证图像的清晰度。扫描时选取试样土体颗粒和孔隙比较均匀的区域，保证扫描区域具有代表性和普遍性。对试样分别采用的放大倍数为500、2 000进行整体与局部的形貌特征观测拍摄。

(5)采用Image-Pro Plus图像软件处理技术对蠕变前后的SEM图像进行处理，得到软土微观结构颗粒和孔隙的相关参数指标，定性定量分析微观结构的变化情况。

试验选取珠三角地区的广州番禺软土，对原状试样和分别在50、100、200、300、400 kPa 6个不同轴向应力水平下固结蠕变后的试样制作成扫描电镜的试样，分别对试样的水平方向和垂直方向进行微观结构特征的观测，土样的基本物理性质如表1所示。

表1 试样的基本物理性质指标

2 试验结果分析

2.1 固结蠕变微观结构定性分析

土体的结构也称为土的微观结构，土体微观结构定性分析主要包括颗粒间接触形式、土中黏土矿物类型、土的结构类型、连结方式、孔隙的连通性等，大量试验数据以及科研工作者研究发现，两种不一样的土体，其力学特性差别很大，说明不一样的土体，有着不一样的结构和构造，表现出不同的力学特性。对软土蠕变前后的SEM图像分析，能够获得许多描述软土微观结构和其变形的参数指标，这些微观参数可以描述番禺软土在不同的轴向荷载作用下蠕变变形过程中。土体颗粒或者孔隙相应变化特性和大小形态、排列特征，主要采用定性和定量的分析方法来研究，定性分析主要获得土的结构类型、连结方式、土中有机物的类型、土颗粒间接触形式、孔隙的连通性等；定量分析主要获得土体颗粒和土中孔隙的个数、丰度、形状复杂度、定向频率等。

选取了7个微观参数来反映颗粒和孔隙的形态特征，定量分析软土蠕变变形的微观结构变化规律。各土体微观结构参数如下：

(1)个数n：土体颗粒(孔隙)的数量。

(2)丰度C：丰度C是描述土体颗粒或孔隙在二维平面内所展示的形态特征，是指其在观测窗口内短轴与长轴的比值，如式(1)所示，丰度C值在(0，1)之间，C值越大，表示颗粒(孔隙)越趋向于等轴圆形；C值越小，则其越趋向于扁长条形。

(1)

式(1)中：B为颗粒(孔隙)的短轴长度，μm；L为颗粒(孔隙)的长轴长度，μm。

(3)颗粒(孔隙)的平均直径：先计算出大小不等，形状各异的各颗粒(孔隙)的面积,然后取等面积圆的直径作为该颗粒(孔隙)的平均直径D(μm)，如式(2)所示：

(2)

式(2)中：A为颗粒(孔隙)的面积，μm2。

(4)形状复杂度e：用离散指数描述颗粒(孔隙)的形状复杂程度，如式(3)所示，反映了区域单位面积的周长的大小，值越小，单位面积的周长越小，区域越紧凑，则颗粒(孔隙)的形状越简单；反之则复杂。

(3)

式(3)中：S为颗粒(孔隙)的周长，μm。

(5)分形维数Ds：颗粒(孔隙)的分形维数跟等效周长L的对数成正比关系，跟面积A的对数成反比关系，如式(4)所示，形态分形维数越大，结构越复杂。

(4)

式(4)中：L为颗粒(孔隙)的等效周长，μm；C为常数。

(6)定向频率F：根据测量对象定向角(长轴与水平线的夹角)的分布用一定的角密度,将分成若干份，计算定向角落入每个区间的频率。通常规定，划分成18个定向角区域，用来表示各定向角区间的结土体颗粒或孔隙的频率，计算公式为

(5)

式(5)中：nα为定向角落[θi-1,θi]的颗粒(孔隙)数量；n为总的颗粒(孔隙)数量。

(7)定向概率熵Hm：反映软土微观结构颗粒(孔隙)排列的有序性[9]，定向概率熵定义为

(6)

式(6)中：Pi为颗粒(孔隙)在某一方位区中呈现的概率；α为颗粒(孔隙)最长弦所对应的方位角；n为颗粒(孔隙)排列方向的定向角区间数。

通常来说，定向概率熵Hm越小，说明颗粒(孔隙)排列的有序性就越好；Hm越大，说明颗粒(孔隙)排列的有序性越差。Hm值在[0,1]之间，当Hm=0时，说明全部的颗粒(孔隙)排列方向都在同一方向，此时颗粒(孔隙)排列的有序性最高；当Hm=1时，说明颗粒(孔隙)完全随机排列，在不同的位区中，颗粒(孔隙)出现的概率相同。

2.2 番禺软土固结蠕变前的微观结构特征

图1是蠕变试验前广州番禺软土原状试样放大500倍和2 000倍的SEM图像。从图1(a)、图1(c)可以看出番禺原状土样放大500倍，微观结构主要是蜂窝状、基质状结构，也有凝块状结构存在。土体排列有明显的特征，土体呈平行片状，集粒间以叠状形式排列较多，土体颗粒排列较紧凑，孔隙较小。虽同为一种土，但在放大2 000倍的图像中展现的微观结构有明显的不同，说明番禺软土结构较为复杂。从图1(b)可以清晰地看到，有少量粉砂分布在土体表面，单个的粉粒通过颗粒间点接触方式与集粒牢固连接，土体颗粒大小均匀，外表棱角可见，土体孔隙较少。图1(d)中有弯曲不规则的蜂窝状结构的有机物成分，孔隙小而整齐，还有长棒型的有机物。经分析为有机质硅藻土和植物根茎遗骸。单独颗粒出现的很少，通常都是由一些黏粒构成的微聚体，进一步形成更大的凝聚体。

对比水平和竖直方向的图像发现，番禺软土各向异性特性明显，水平方向微观结构主要以蜂窝状为主，颗粒排列稀疏，颗粒间以点接触为主，微生物和有机物较少；竖直方向则以基质状结构为主，颗粒间以面-面接触为主，含有大量的有机物，孔隙小而多。

图1 番禺软土原状试样的微观结构

2.3 固结蠕变后软土的微观结构特征

图2为番禺软土分别在轴向应力为50、100、200、300、400 kPa下蠕变后的放大500倍和2 000倍的微观结构图像。由图2可以看出，番禺软土随着固结压力不断增大，土体中的大颗粒大孔隙数量不断减少，小颗粒小孔隙不断增多。说明固结蠕变过程中，土体结构遭到破坏，大颗粒被压破变成小颗粒，大孔隙被压缩成小孔隙或被新形成的颗粒填充，土体变的密实。

2.4 孔隙和颗粒的丰度及复杂度

由SEM图像易知，番禺软土在不同试验条件下，微观结构的颗粒和孔隙的形状各有不同，而且表现着不同着宏观力学特性。为了更加真实的描述微观结构的实际情况和衡量结构单元体的圆滑程度，选取颗粒和孔隙的丰度和复杂度进性分析。

通过IPP软件直接求出土体颗粒和孔隙的长轴与短轴，然后用式(1)计算出颗粒或孔隙的丰度，由丰度的定义可知，当丰度值接近1时，表明土体颗粒或孔隙的形状接近圆形；当丰度值在0.5附近时，其形状接近扁椭圆形；当丰度值接近0时，表明土体颗粒或孔隙的形状接近长条形。通过软件计算测量对象的面积与周长，用式(2)计算出颗粒或孔隙的复杂度，e值越小，其形状越简单；e值越大，其形状越复杂。表2和表3分别是土体颗粒和孔隙在蠕变前后微观结构的丰度与复杂度。

图2 轴向应力在不同固结压力下蠕变后的SEM照片

将表2和表3的数据转换成条形图，如图3～图5所示。由图3可知，原状土颗粒的复杂度低于孔隙的复杂度，随着轴向应力增加，颗粒的复杂度从23.14降为19.04，孔隙的复杂度从29.65降为26.79。颗粒和孔隙的复杂度都有所减小，其形状趋向简单化。

表2 原状土和蠕变后土样微观结构的颗粒丰度和复杂度

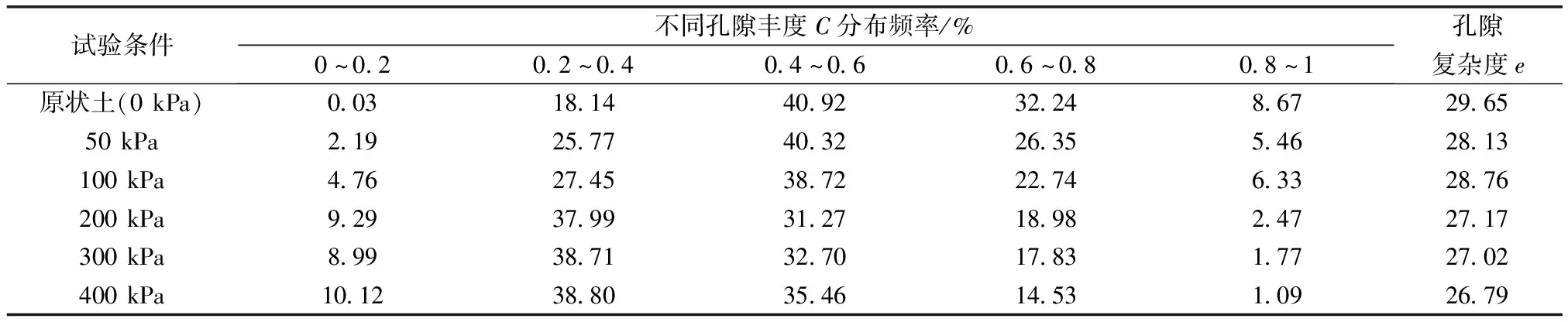
表3 原状土和蠕变后土样微观结构的孔隙丰度和复杂度

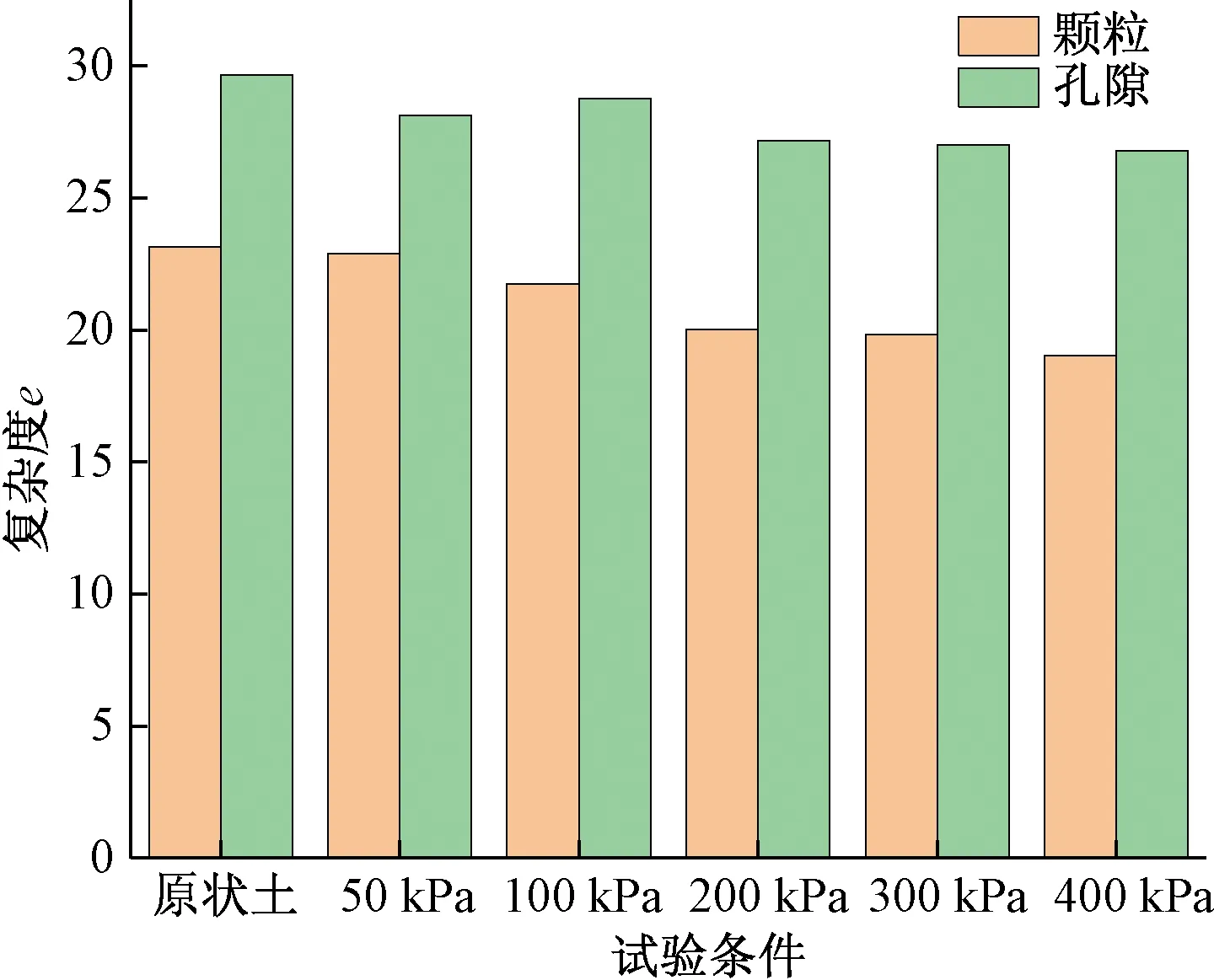
图3 不同试验条件下土体颗粒孔隙复杂度

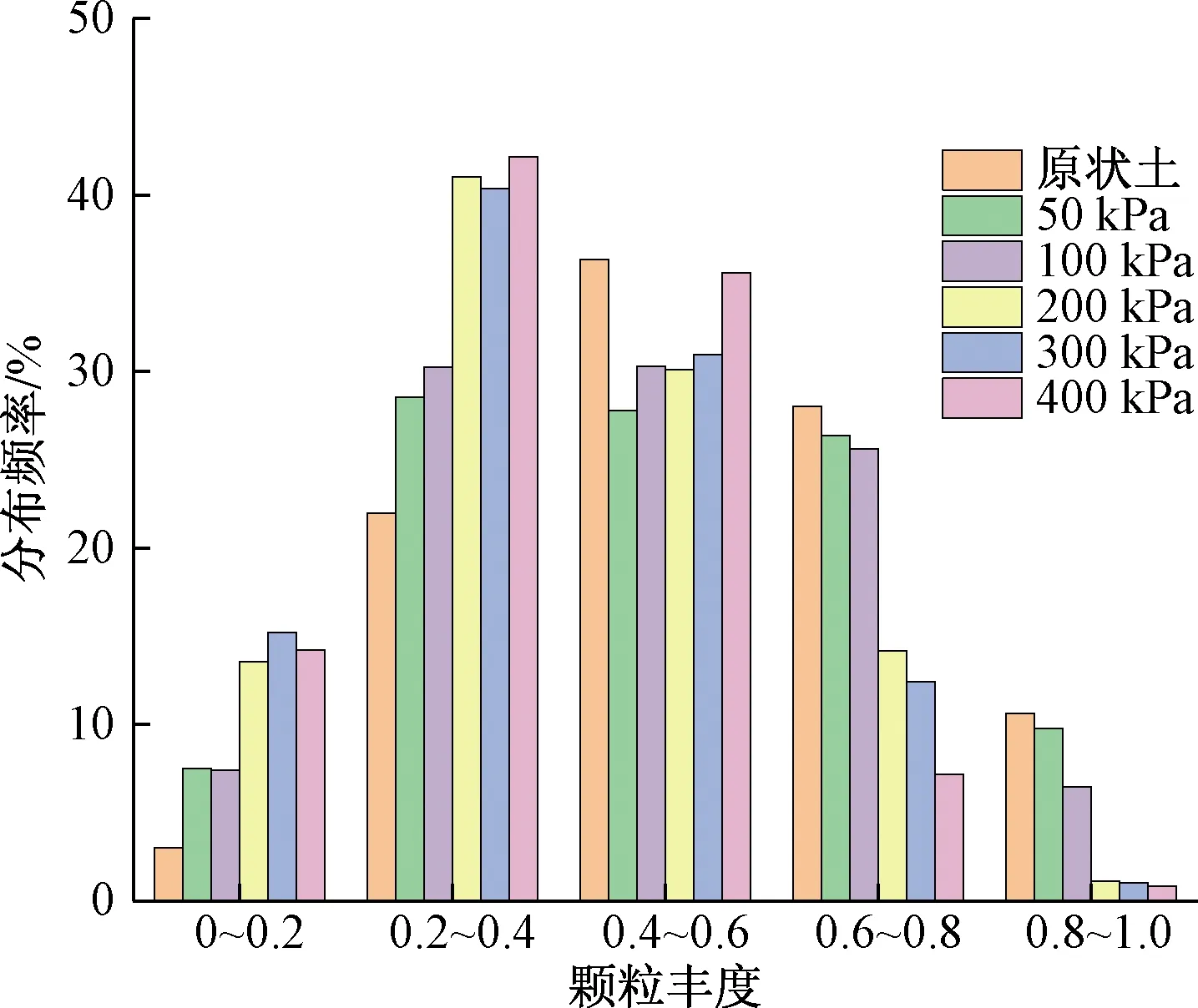
图4 不同试验条件下土体颗粒丰度分布

图5 不同试验条件下土体孔隙丰度分布

由图4可知，原状土中颗粒的丰度在0.4～0.6区间所占的比例最高，在0～0.2区间所占的比例最低，在区间0.6～0.8、区间0.2～0.4、区间0.8～1所占的比例依次递减。从这所占比例的分布来看，番禺原状土样中颗粒形状主要以近椭圆为主，近长条形和近圆形的颗粒比较少。随着轴向应力的加大，土体颗粒丰度在0～0.2区间所占比例有所提高；在0.2～0.4区间颗粒丰度逐渐提高，增长幅度较大；区间为0.4～0.6的颗粒所占比例先降低后提高，最后跟原状土样的持平；区间在0.6～0.8和0.8～1的颗粒所占比例随轴向应力增加而降低。从不同试验条件下颗粒丰度的变化情况可知，随着轴向压力的增长，土体的颗粒形状不断向扁平化发展，但仍然以椭圆状为主。

从图5能看出，原状土的孔隙丰度主要集中在区间0.4～0.6和区间0.6～0.8，而其他三个区间所占比例较小，表明番禺原状土样的孔隙形态以扁椭圆状和近椭圆状为主，近长条形和近圆形所占比例很小。当轴向应力不断增大时，孔隙丰度在0.6～0.8区间的所占比例大幅度的降低，在0.8～1区间的有所降低；而区间0.4～0.6的孔隙丰度所占比例先增加后降低，变化幅度不大；区间0～0.2和区间0.2～0.4的所占比例随着轴向荷载的增长而增长，其中区间0.2～0.4的增长幅度达到20%以上。总体而言，土中的孔隙主要以扁椭圆状和近椭圆状存在，孔隙形态会随着轴向应力的增加而发生变化，但还是处于近椭圆状。

图6 不同轴向应力下分形维数计算曲线

结合表2、表3和图3～图5，土体发生蠕变后，颗粒和孔隙的复杂度都有所降低，相比孔隙，颗粒的复杂度降低的更多。颗粒和孔隙的形态随着土体有效应力的增长和孔隙水压力的消散而逐渐的向近椭圆状发展，使得颗粒和孔隙越来越“圆滑”。

2.5 孔隙分型维数

利用IPP软件能直接计算出土中孔隙的等效周长和面积，通过式(4)可以得到不同蠕变条件下的lgL和lgA散点图，进行函数拟合(图6)。由图6可知，孔隙等效周长的对数跟面积的对数呈线性关系，且相关系数都在0.93以上。基于分形维数DS与拟合直线的斜率K存在DS=2K关系，可以求出分形维数DS，如表4所示。

由表4可知，番禺原状土样的分形维数高于土体蠕变变形后的分形维数，因为原状土样的孔隙结构复杂程度最大，即孔隙表面特性偏离光滑表面的程度最远。当轴向应力增大时，土中孔隙的分形维数不断的减小，说明土中的孔隙随着轴向应力的增大而不断的变得简单，在蠕变变形过程中土中的孔隙被挤压，大孔隙不断地减少，小孔隙不断地增加，在此过程中，土体颗粒也相应地变化，大颗粒破损，小颗粒被挤入大孔隙中，颗粒和孔隙朝着均匀化方向发展，使得土体结构越来越简单。分形维数能描述土体颗粒和孔隙的复杂性的变化，也能反映出土体的宏观变形的机理。

表4 分形维数

2.6 结构定向分析

土体颗粒和孔隙的定向频率能简单直观地反映总体定向特性，通过IPP软件自动计算出每个测量对象的长轴与水平线的夹角，如图7所示。根据孔令荣等[10]提出的土团粒镜像对称假定，即假定土团粒的定向角在0°～360°内是镜像对称的。因此只对0°～180°范围内的土体颗粒和孔隙的定向频率进行分析。将180°划成18个等角密度的定向角区域，用式(5)分别计算出颗粒和孔隙在不同试验条件下的定向频率(图8)。

图7 颗粒定向方向角示意图

由图8可知，原状土样颗粒的定向性并不是很明显，而土中孔隙的定向分布较好，大多数集中在80°～90°和90°～100°的区间内，这可能与原状土样的应力释放引起的松动有关。随着固结压力的增加，颗粒的定向性越来越显著，逐渐往120°～150°区间分布，而土中孔隙定向性随之而消失，定向角度区间趋于平均，说明番禺软土在蠕变后，颗粒的定向变得更有序，孔隙定向性变的混乱。主要是在蠕变变形的过程中，土体受到外界的荷载作用下发生压缩，颗粒受到挤压后调整自身的形态或者挤裂破损去适应外界荷载的变化，而受到土体的压缩、颗粒的调整和破碎的影响，长条形孔隙趋向扁圆形，孔隙的定向性降低，方向角较混乱。

采用定向概率熵Hm反映软土微观结构颗粒和孔隙排列的有序性，通常来说，定向概率熵Hm越小，说明颗粒(孔隙)排列的有序性就越好；Hm越大，说明颗粒(孔隙)排列的有序性越差。表5为番禺软土蠕变前后颗粒和孔隙的定向概率熵。由表5可知，番禺土体的概率熵都0.805以上，颗粒和孔隙的排列从整体上看较为无序。

由图9可知，番禺原状土样的颗粒的定向概率熵较大，说明定向性不明显，孔隙的定向概率熵较小，定向性较好。随着轴向荷载的增加，颗粒的定向概率熵不断地减少，颗粒的定向性加强，从无序向有序转变；孔隙的定向概率熵不断地加大，定向性减弱，从有序向无序变化，这结论跟定向频率的分析结果相吻合。

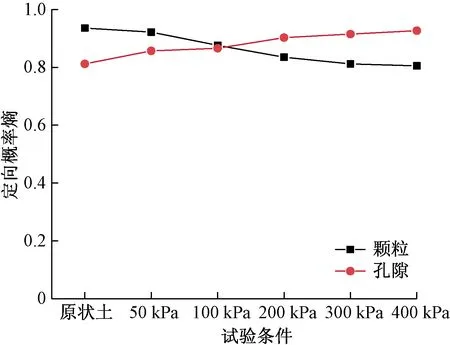
图9 不同试验条件下土体颗粒和孔隙的定向概率熵

3 结论

通过对原状土和不同固结压力下蠕变后的土样进行扫描电镜试验，对番禺软土进行了微观结构方面的研究，并采用IPP图像处理软件进行微观结构参数的处理，得出以下几点结论：

(1)番禺原状土样的微观结构主要是以蜂窝状和基质状结构为主，土体颗粒接触方式主要为边-边接触和边-面接触；当施加轴向固结荷载时土体的结构发生变化，轴向荷载较大时，土体的微观结构以紧密的骨架状和紊流状结构为主，土体颗粒的接触方式以面-面接触为主。

(2)番禺软土在蠕变过程中，土体颗粒和孔隙大小的变化都遵循大孔隙优先改变原则，颗粒和孔隙的轮廓变得“圆滑”且形状趋向于扁圆形。蠕变后，颗粒和孔隙的个数有明显的增加、直径都有明显的减少、丰度值和复杂度有所降低。

(3)番禺原状土样的分形维数高于土体蠕变变形后的分形维数，当固结应力增大时，土中孔隙的分形维数不断的减小，大孔隙不断地减少，大颗粒破损，小颗粒被挤入大孔隙中，颗粒和孔隙朝着均匀化方向发展，与对微观结构丰度和复杂度的分析结果相吻合。

(4)番禺原状土样颗粒的定向性并不明显，而土中孔隙的定向分布很好。随着固结压力的增加，颗粒的定向性越来越显著，而土中孔隙定向性随之而消失，定向角度区间趋于平均。这说明番禺软土在蠕变后，颗粒的定向变得更有序，孔隙定向性变的混乱，这与定向概率熵的分析结构相一致。