重载铁路路基动回弹模量影响因素及预估模型分析
2020-05-25宋慧来薛明星冯怀平张彩亮
宋慧来,薛明星,冯怀平*,张彩亮
(1.石家庄铁道大学土木工程学院,石家庄 050043;2.华邦建投集团股份有限公司,兰州 730030;3.中国铁道科学研究院研究生部,北京 100081)
近年来,重载铁路由于其可观的经济效益和社会效益而迅速发展,其运营安全也越来越引起广泛关注[1]。与此同时,由Seed等[2]提出的动回弹模量作为评价路基土体性能的关键参数已经得到广泛认可。通过动回弹模量,可以直观、准确地表征路基土体抗变形能力,反映土体刚度。重载铁路路基作为支撑重载铁路的重要构筑物,同时承受路基上部静荷载以及列车循环荷载,且对于不同的路基工作区域,其围压与动应力组合不同,这必将导致其所表现的刚度特性不同[3]。因此,通过合理地应力组合对重载铁路路基不同工作区域内的动回弹模量进行科学的测定,可以为预测路基结构稳定、保障列车轨道平顺运营提供重要的理论基础和实用价值。
目前,众多研究者们普遍采用动三轴试验测定路基土体动回弹模量值。而关于动三轴试验加载序列的确定,陈声凯等[4]通过对中国139个实际路面结构进行计算统计,确定了符合沥青路面路基土体的动三轴加载序列;段丹军等[5]则针对运煤重载黄土地区,建立符合高速、一级、二级公路的路基动回弹模量动三轴试验加载序列。但是由于重载铁路远超普通公路、铁路的大轴重运输特点,重载铁路路基会承受较高的动应力加载,应力组合明显不同,以上加载序列并不适用。因此有必要对动三轴加载序列进行重新设计,以符合重载铁路路基有效工作区域内的应力组合。
Mehrotra等[6]和Salour[7]研究发现动回弹模量除了受应力状态的影响,还具有强烈的湿度依赖性,当土体含水率发生变化时,动回弹模量也会随之变化。Gabr等[8]和Liang等[9]认为土体的回弹特性很大程度上受到自身土层的密实程度与外界施加的应力状态的影响。而在实际工程中,路基含水率存在差异,且由于施工技术缺陷、外界条件变化等诸多因素的影响,路基压实程度难以精准、持续控制,因此有必要探讨不同含水程度和不同压实程度对动回弹模量的影响。本文以含水率控制土体含水程度,干密度控制土体压实程度。
关于动回弹模量预估模型的构建,初始研究者建立的模型[10-12]仅考虑单一应力,对其余影响因素考虑不足,且存在量纲问题,虽应用简单却难以推广。Uzan[13]在单一模型的基础上,提出了体应力、偏应力的复合模型,解决了量纲问题,但仍存在模量不定值问题。Ni等[14]则对Uzan模型更进一步进行优化,不仅提高了模型精度,还解决了模型不定值与量纲问题,建立了回弹模量与围压、偏应力相关的复合模型,并具有良好的适用性。因此,选择Ni模型作为重载铁路路基动回弹模量预估模型。
通过对动三轴加载序列进行重新设计,模拟重载列车运行时路基有效工作区域的实际应力状况。同时基于湿度状态[15]和压实状态[16]对土体力学性质的重要影响,开展3种湿度状态和3种压实状态以及12种应力状态下的动三轴试验,以探讨不同的应力组合(动应力和围压)以及不同的土体状态(含水率和干密度)对路基土体动回弹模量的影响。甄选动回弹模量预估模型,并以试验数据基础进行拟合分析,从而为重载铁路路基设计提供理论基础和经验参数。
1 动三轴加载序列确定
1.1 设计原则及预载确定
在进行室内加载序列的应力组合设计时,旨在涵盖铁路运营期间,路基土体有效工作区域出现的所有常见应力状况范围,并在保证土样刚度稳定的前提下,对应力组合进行序列分布与振次配置,最后构建出重载铁路路基室内测试动回弹模量加载序列。
在序列加载正式开始前,为去除先期应力历史造成对土体的差异影响,并消除试样与仪器的不完全接触以及制样缺陷所带来的动回弹模量突变现象,需进行一定振次的预加载作用,保证试样以良好的刚度稳定状态进入序列加载阶段。为模拟运营期间的实际列车加载轴重,采用90 kPa作为预载阶段的动应力幅值,配置加载次数1 000次。
1.2 应力组合确定
根据现场实测重载铁路列车的动应力响应发现,其动应力幅值主要在80~100 kPa,而基床围压应力一般在25~60 kPa。根据设计原则,并考虑铁路扩能改造带来的动应力幅值扩增,试验加载动应力幅值设定为80、100、120、140 kPa,围压采用30、45、60 kPa。试验接触荷载设定为围压的20%,以模拟路基上部静荷载,并保证在试验全程试样处于受压加载状态。
1.3 加载序列确定
在进行序列布置时,采用大围压、小动应力幅值先行,围压逐渐递减,动应力幅值逐渐递增的设计思路。循环加载次数一般为100~200,采用100次作为每一序列加载阶段的加载次数。具体加载序列设计如表1所示。

表1 动三轴试验加载序列
2 动三轴序列加载试验
2.1 试验仪器
试验采用英国GDS公司生产的DYNITS动静三轴系统,主要由计算机、高速采集仪、压力罩、围压和反压控制器等组成,如图1所示。其中计算机除了在试验开始前,按照拟定的试验方案设置所需的试验参数,还可以在试验进程中对于应力、应变等各项指标的变化进行实时监控,以保证试验进程的有效性;而高速采集仪主要针对试验产生的各项数据进行自动采集,包括轴向应力、轴向应变、围压、动偏应力、试验时间等各项指标;动三轴试样装在压力罩内,内有传感器和加载装置,可以确保在对土样进行试验的同时,实时测试相关指标;围压和反压控制器可以保证在试验时对压力罩内的围压和反压进行实时调控,以保证所需的试验环境。

图1 GDS动三轴试验系统
2.2 试验土样
试验土体取自包神铁路某病害段,根据《铁路工程土工试验规程》[17]和《土工试验规程》[18]对土体进行制样,试样直径61.8 mm,高度125 mm,土样基本物性参数如表2所示。

表2 基本物性参数
2.3 试验方案
试验采用上述制定的重载铁路路基室内加载序列进行加载,考虑实际工程中出现的不同干密度和不同含水率的状况,制出干密度分别为1.5、1.6、1.7 g/cm3和含水率分别为10%、13%、16%的动三轴试样进行试验,每组试验重复进行3次平行试验,共计27组试验。具体试验方案如表3所示。
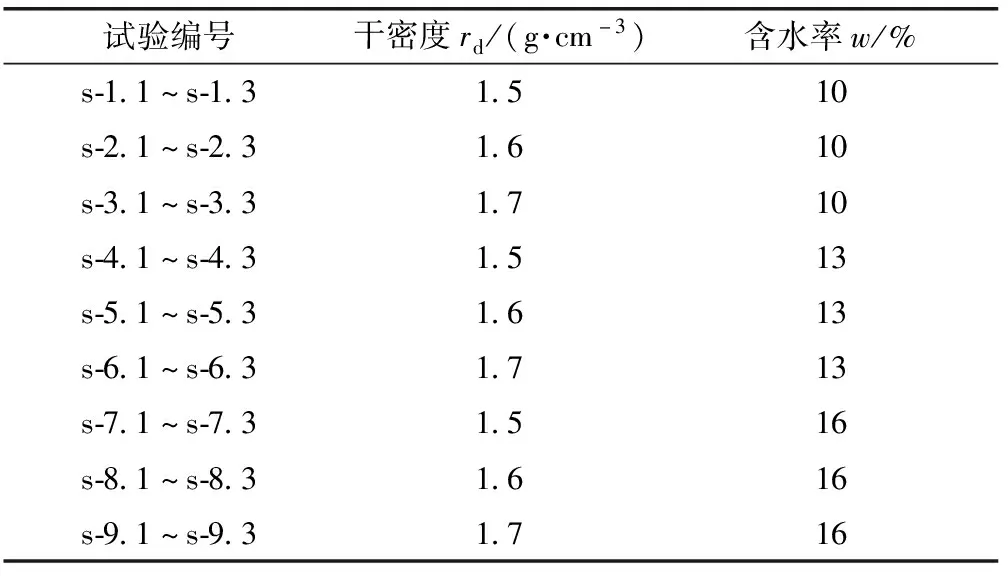
表3 试验方案
2.4 动回弹模量计算
动回弹模量由土体外界的应力状况与自身的弹性变形所共同决定,计算示意图如图2所示。计算公式如下:
(1)
式(1)中:Mr为动回弹模量;σd为动偏应力幅值;εr为弹性应变。
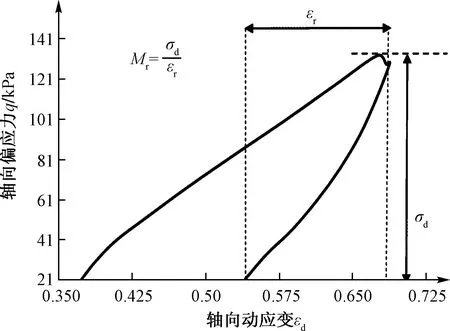
图2 动回弹模量计算示意
3 影响因素分析
3.1 动应力幅值对动回弹模量的影响
图3给出了各含水率(w=10%、13%、16%)和各干密度(ρd=1.5、1.6、1.7 g/cm3)试样在不同围压状态下(σ3=30、45、60 kPa)动回弹模量随动应力幅值的变化。可以看到,对于在27组动三轴加载试验中随机选取的3组试验,动应力幅值较小时动回弹模量较大,而随着动应力幅值的增加,动回弹模量明显减小。将动回弹模量随动应力幅值增大而减小的程度定义为动回弹模量减小率,则当动应力幅值由80增加到140 kPa时,动回弹模量减小率如表4所示,且经计算动回弹模量平均减小率为9.77%。这主要是因为动应力幅值增大会造成土体在每一个循环加载过程中的弹性应变增大,从而导致动回弹模量减小。在不同的围压状态下,动应力幅值对动回弹模量的影响规律相似,且不同的初始状态(不同含水率和不同干密度)会造成土体的动回弹模量值差异。
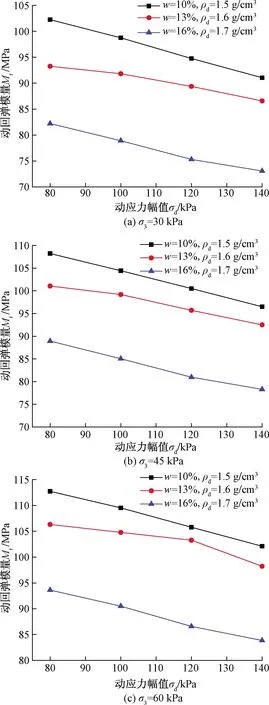
图3 动回弹模量-动应力幅值关系曲线
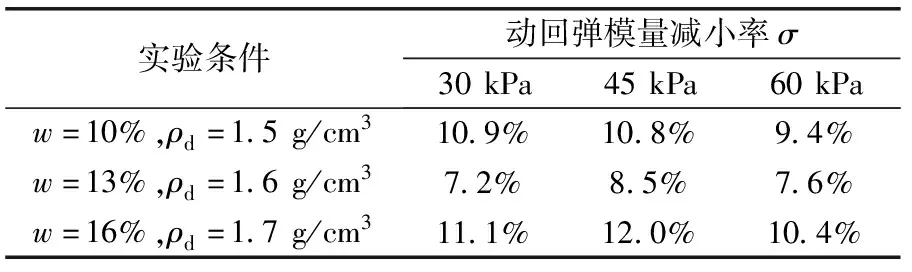
表4 动回弹模量减小率
3.2 围压对动回弹模量的影响

图4 动回弹模量-围压关系曲线
图4给出的是各含水率(w=10%、13%、16%)和各干密度(ρd=1.5、1.6、1.7 g/cm3)试样在不同动应力幅值状态下(σd=80、100、120、140 kPa)动回弹模量与围压的变化关系。可以看到,对于在27组动三轴加载试验中随机选取的3组试验,围压较小时动回弹模量较小,而随着围压的增大,动回弹模量也随之增大。将动回弹模量随围压增大而增大的程度定义为动回弹模量增长率,则当围压由30 kPa增长至60 kPa时,不同含水率和干密度土体动回弹模量增长率如表5所示,且经计算动回弹模量平均增长率为16.16%,变化比动应力幅值的影响较大。这主要是因为围压增大会造成土体在每一个循环加载过程产生的弹性应变减小,从而动回弹模量增大。在不同的动应力幅值加载下,动回弹模量与围压的变化关系相似,且不同的初始状态(不同含水率和不同干密度)会对动回弹模量值的大小造成差异。
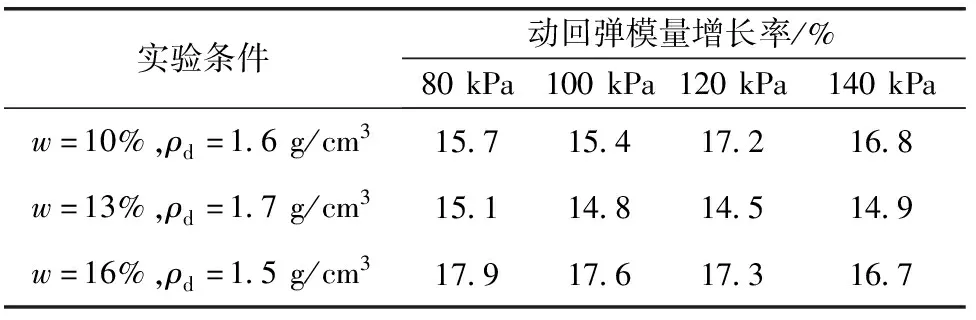
表5 动回弹模量增长率
3.3 含水率对动回弹模量的影响
为研究土体不同的初始含水率对动回弹模量的影响,绘制了不同应力组合下的动回弹模量与含水率关系曲线,如图5所示。可以看出,随着土体含水率的增大,动回弹模量显著下降,且不同围压状态下的动回弹模量下降规律相似。图5中曲线的斜率可以代表动回弹模量的下降速率,当动应力幅值较小时(σd=80、100 kPa),动回弹模量下降速率随含水率增大而加快;当动应力幅值较大时(σd=120、140 kPa),动回弹模量下降近似呈线性下降,下降速率基本不变。这表明在较大的动应力幅值作用下,土体含水率增大对动回弹模量下降速率的影响在减弱。
3.4 干密度对动回弹模量的影响
图6为不同的动应力和围压应力组合下动回弹模量与干密度的变化关系曲线。可以看出,随着土体干密度的增加,动回弹模量明显增大,且不同围压状态下的动回弹模量增长规律相似。图6中曲线的斜率可以代表动回弹模量的增长速率,当动应力幅值较小时(σd=80、100、120 kPa),随着干密度增大,动回弹模量增长速率逐渐减小;当动应力幅值达到140 kPa时,动回弹模量增长速率近似呈线性增长。这表明在较大的动应力幅值作用下,土体干密度增大对动回弹模量增长速率的影响在减弱。
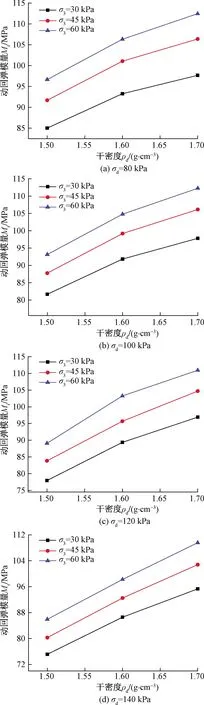
图6 动回弹模量-干密度关系曲线
4 重载铁路路基动回弹模量预估模型
由上述分析可知,动回弹模量对动应力及围压具有较高的敏感性,因此选取综合考虑动应力和围压影响的Ni模型对路基动回弹模量进行分析,其方程如式(2)所示:
(2)
根据选取的预估模型,对不同含水率和不同干密度的试样数据进行拟合分析,拟合结果如表6、图7所示,可以看出拟合结果良好。此外,由表6可以看出,回归系数R2均在0.98以上,因此用该模型对动回弹模量进行预估具有较高的精度。
5 结论
(1)确定了符合重载铁路特点的路基土体动三轴加载序列,具体加载序列见表1。
(2)分析了应力状态对土体动回弹模量的影响,动回弹模量随动应力幅值的增大而减小,平均减小率为9.77%;动回弹模量随围压的增大而增大,平均增长率为16.16%,影响较动应力幅值显著。
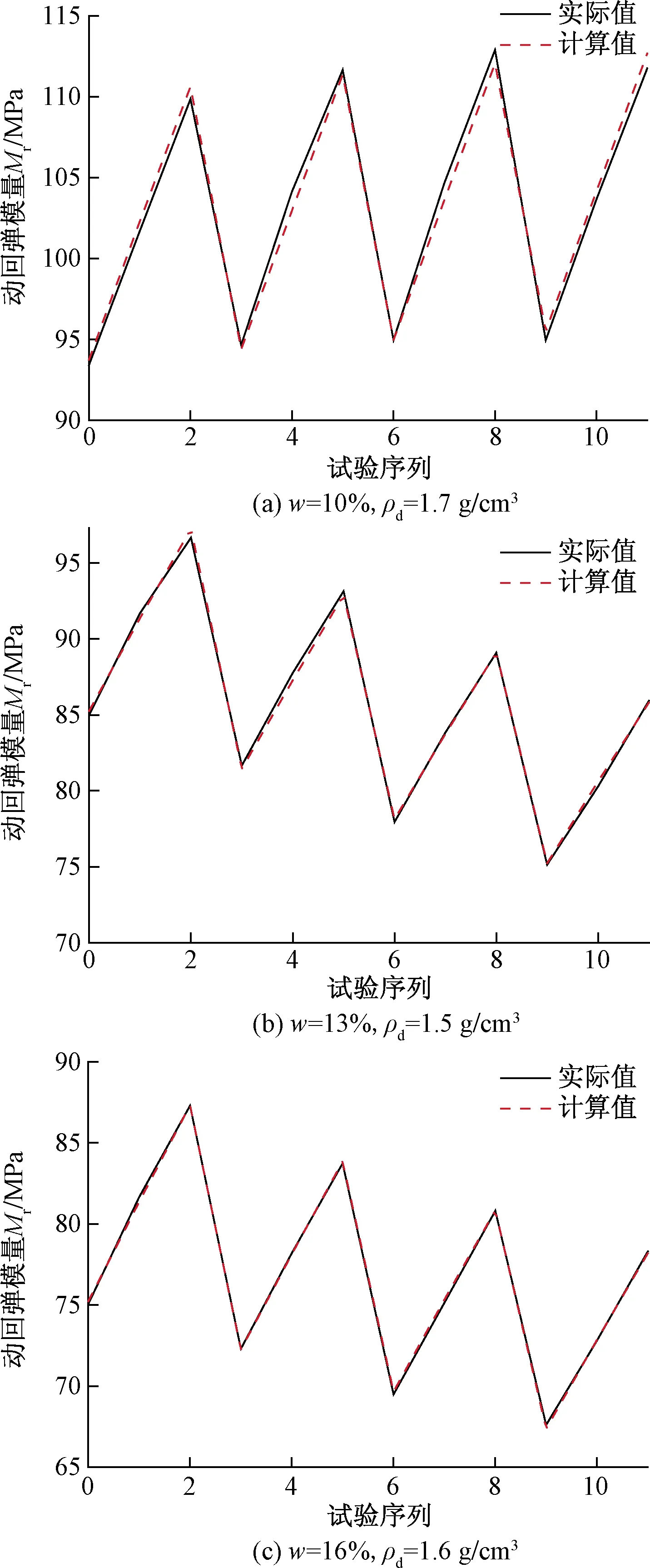
图7 模型数据拟合图

表6 数据拟合结果
(3)土体初始状态对动回弹模量存在影响,动回弹模量随着含水率的增大而下降,随着干密度的增大而增长,且动应力幅值会影响下降(增长)速率,动应力幅值越大,动回弹模量下降(增长)速率越趋近于线性变换。
(4)采用Ni模型进行重载铁路路基动回弹模量预估,结果具有极好的精度,可为重载铁路路基结构设计提供理论依据和经验参数。
