矩形薄壁钢管混凝土短柱轴心受压性能试验研究

张忠杰,周新刚,宋振宇,李 伟,宋维国

(烟台大学土木工程学院,山东 烟台 264005)

矩形钢管混凝土构件与圆形、方形钢管混凝土构件最明显的差别在于其截面形状不同.截面形状的差异将在很大程度上影响钢管对混凝土的套箍作用.在圆形钢管混凝土中,核心混凝土受到均匀约束;在矩形钢管混凝土中,核心混凝土受到的约束不均匀,截面中部和角部受到的约束大,长、短边中部受到的约束小.较圆形和方形截面的钢管混凝土结构,矩形钢管混凝土结构在横截面长边方向上的约束弱,整体的有效约束区小,因此不管是内侧的核心混凝土还是外侧的钢管,与传统的圆、方截面的钢管混凝土结构相比其受力性能更为复杂[1-6].一些学者对此作了大量试验研究.韩林海等[7]进行了24个矩形截面钢管混凝土轴心受压短柱的试验,得出矩形钢管混凝土试件轴心受压时的力学性能与约束效应系数和长宽比有关.李黎明[8]研究了矩形钢管混凝土轴压短柱试件力学性能,使用有限条分法并结合试验结果,得出在矩形钢管混凝土构件中,钢管管壁与核心混凝土之间的粘结力属于弱粘结.杜颜胜[9]进行了2批共21个高强钢矩形钢管混凝土试件的轴心受压试验,试验试件主要考察了宽厚比和长宽比的影响.

最近几年钢管束混凝土剪力墙或多腔钢管混凝土剪力墙结构得到应用.在这种结构中,一般使用3～5 m的薄钢板.研究表明[10-13],在水平力及竖向荷载的作用下,边缘钢管束主要承受压力或拉力,其性能对整体墙的影响较大.本文通过32个矩形薄壁钢管混凝土短柱的轴心受压试验,分析在轴压的全过程中薄壁钢管对核心混凝土的约束作用及工作机理,根据其受力机理提出一种矩形薄壁钢管混凝土短柱轴压承载力的简化分析方法,得到极限承载力计算公式.

1 试验研究

1.1 试验概况

本试验研究共设计了16种试件,每种试件制作2个,共32个试件.试件尺寸以及材料参数如表1所示.其中h为截面长度;b为截面宽度;H为试件高度;t为钢板厚度;fcu为实测混凝土立方体抗压强度;fy为实测钢材屈服强度.

表1 试件参数Tab.1 Properties of specimen

1.2 试验方法

试件在5 000 kN压力试验机上进行.试验加载之前,对每个构件进行精确对中,放置好上部加载板,并在试件两侧布置位移计来测量试件的轴向压缩变形.每个试件的长边立面和短边立面的中部各布置了横向、纵向2个应变片,如图1.试验加载制度为:正式试验前先对试件进行预压,预压荷载约为试件预估极限承载力的10%,此时要求对称布置的位移计读数绝对误差在10%以内.正式加载采用分级加载,弹性阶段每级荷载为预估荷载的10%;当荷载增至预估荷载的75%时,改为位移加载以0.5 mm/min的速率加载,直至极限荷载;当荷载降至极限荷载的70%或鼓曲非常严重时,结束加载.

2 试验结果分析

2.1 试验结果与试验现象

试件极限承载力试验结果列于表2,Nue为同种试件实测极限承载力平均值,SR=Nue/(fykAs+fckAc),为试件的强度比[7].加载初期试件处于弹性阶段,钢管混凝土短柱初始(轴向)刚度较大,初期的变形较小.当试件轴向荷载增至极限荷载的70%左右时,试件表面开始发生鼓曲,且试件长边比短边的鼓曲明显.随着外荷载的继续增加,试件达到极限承载力后,钢管混凝土短柱四边鼓曲明显,内部核心混凝土向外臌胀并出现压碎现象.外荷载继续增大,试件中部鼓曲现象急剧发展,最终试件因丧失承载能力而破坏.试件的最终破坏形态如图2所示,钢管的长边和短边均表现出连续半波状鼓曲.试件的强度比-位移曲线及荷载-应变曲线见图3和图4.从强度比来看,随着试件的长宽比增大,试件的弹性刚度逐渐减少,试件的强度比总体也呈现出降低的趋势,但规律不如厚壁试件明显.这是因为:一是轴压过程中薄壁钢管自身的竖向承载能力弱于厚壁钢管,对试件承载力的贡献小于厚壁钢管;二是在核心混凝土发生横向变形的过程中,薄壁钢管比厚壁钢管更易屈曲与断裂,对核心混凝土的环向约束相对较差.

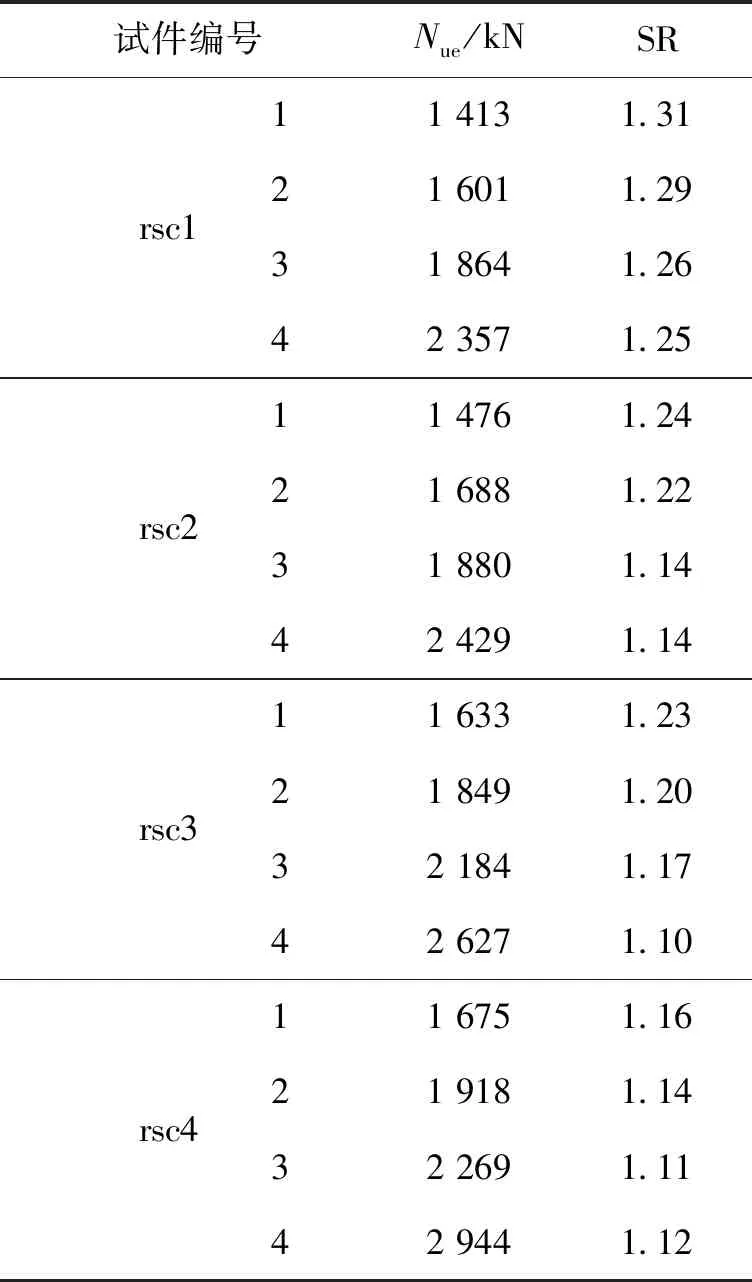
表2 试验结果Tab.2 Test results

2.2 轴压全过程受力机理分析

试件破坏经历了3个阶段:弹性阶段、弹塑性阶段、下降阶段.

弹性阶段:开始加载后,荷载增至极限荷载70%过程中,荷载与位移曲线呈直线上升.70%极限荷载时薄壁钢管的应变如表3所示,钢管的纵向应变均小于钢材的屈服应变2 000με,且钢管的环向应变很小,钢管尚未屈服,竖向与核心混凝土一起承受轴压力,外侧钢管对混凝土的约束作用很小.

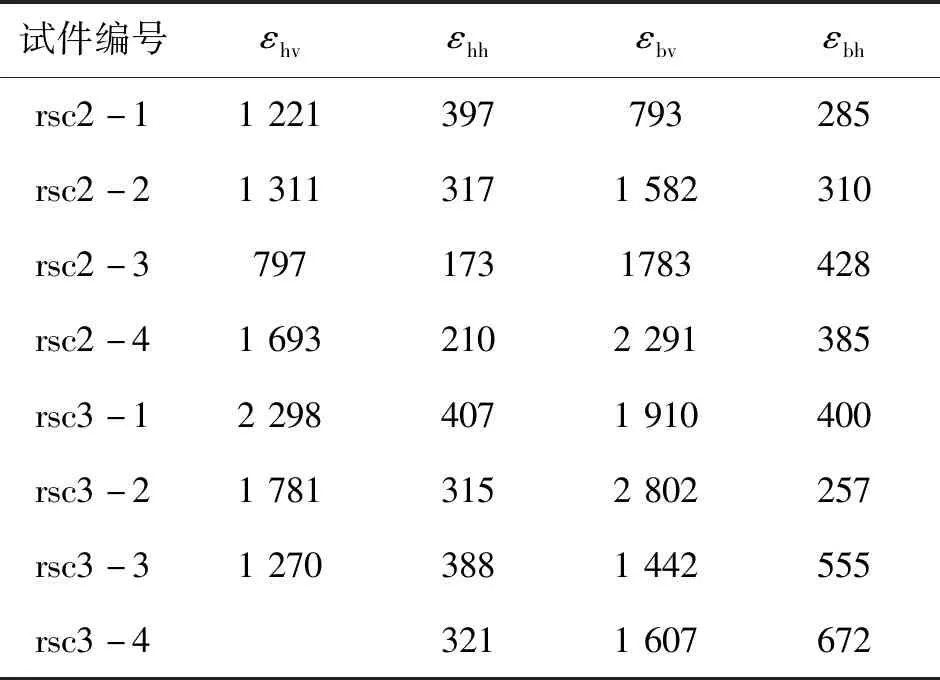
表3 70%极限承载力处的应变Tab.3 70% ultimate bearing capacity strain value

弹塑性阶段:弹性阶段结束至极限荷载的过程中,荷载与位移曲线呈现出非线性的增长趋势．到达极限承载力时,实测钢管的竖向应变约是弹性极限的2.5倍左右,同时钢管的横向应变也大幅度提高,约是弹性极限处的3倍左右,见表4.由于横向应变大幅度增加,说明钢管对核心混凝土起到了约束作用,因此核心混凝土的抗压强度得以提高.由于核心混凝土抗压强度提高,极限承载力也较弹性极限承载力提高.从弹性极限到承载能力最大值,虽然钢管有鼓曲,但钢管仍有承载力,并能约束核心混凝土使其强度提高,最终使总的承载能力比弹性极限点高30%左右.

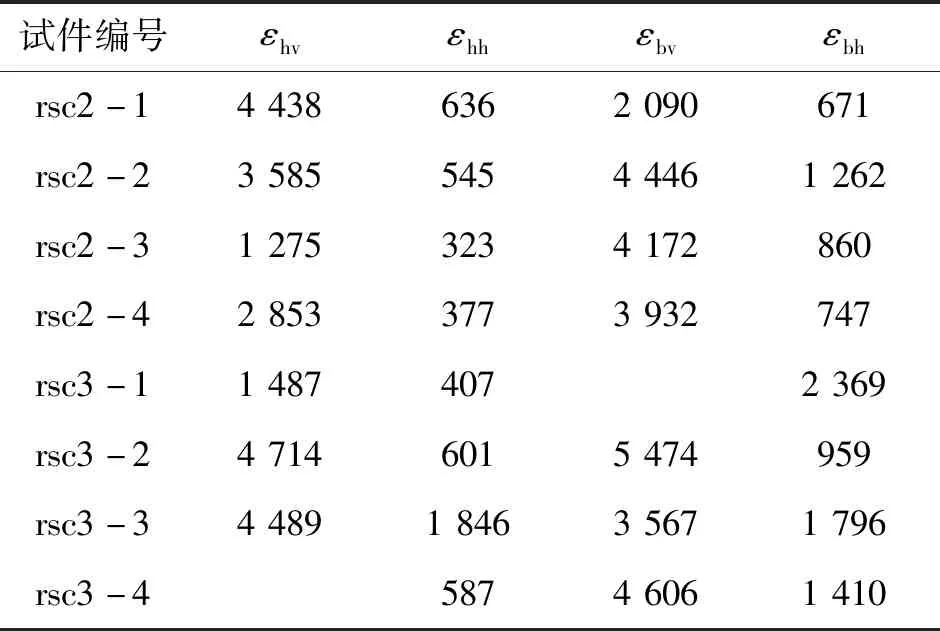
表4 极限承载力处的应变Tab.4 Ultimate bearing capacity strain value

试件的长宽比对弹性阶段的轴压刚度影响较为明显.如表5所示,长宽比越大试件的轴压刚度k越小.因为在此过程中薄壁钢管长边的横向应变小于短边的横向应变,钢管长边对核心混凝土的约束差,在加载过程中长边方向容易发生大的变形.与试验时长宽比较大的试件,长边方向较早的出现鼓曲这一现象相吻合.矩形截面试件的整体刚度弱于方形截面.

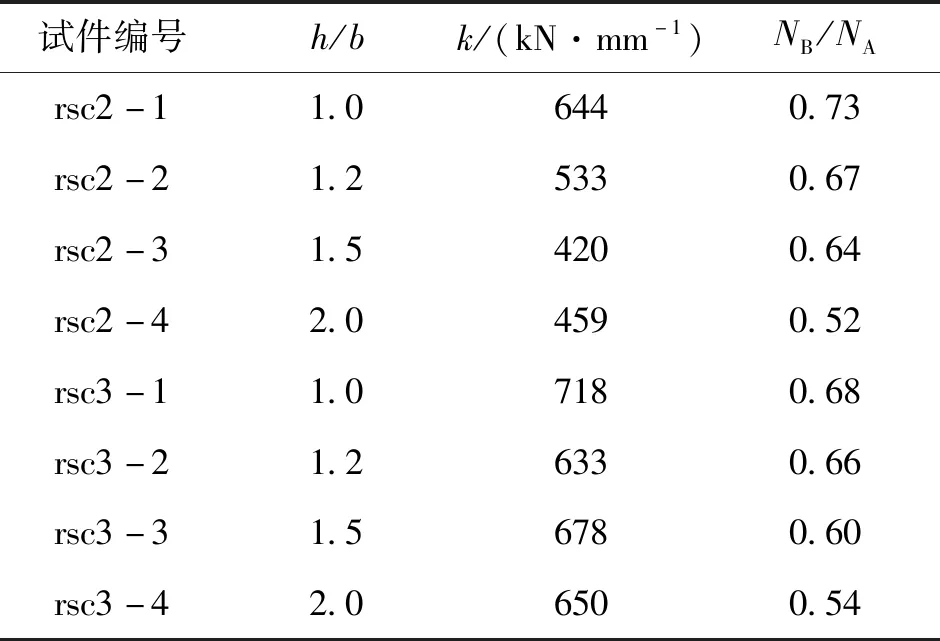
表5 轴压刚度与承载力下降幅度Tab.5 Axial compression stiffness and bearing capacity decline

下降阶段:当达到最大承载力时,钢管鼓曲明显,鼓曲区域对混凝土的约束作用完全丧失,此时不仅内部的混凝土进入下降段,外部钢管的竖向承载力也基本丧失,因此承载力陡然降低,见图3所示.承载力从A点陡降至B点,B点的承载力与A点承载力的关系见表5.可以发现试件的长宽比越大,承载力下降的幅度越明显.陡降至B点后,随着混凝土横向变形不断增大,钢管对混凝土仍有一定约束,在残余承载力不变的情况下,变形继续增加,试件的轴向压缩可达到13 mm左右,这与无约束试件在峰值荷载后承载力迅速降低进而直接破坏是不同的.

3 极限承载力简化计算公式

3.1 基本假定

根据现有的计算理论[14-16],钢管混凝土短柱的轴压极限承载力由两部分组成:外侧钢管承载力+内侧混凝土的承载力.极限状态时,外侧钢管的破坏服从Mises屈服条件,内侧混凝土考虑外侧钢管的约束作用处于三轴受压状态.

对于薄壁矩形钢管混凝土短柱,极限状态时,外侧钢管的屈服仍服从Mises屈服条件,内侧混凝土仍受到外侧钢板的约束而处于三向受压状态.所不同的是:一薄壁钢板的约束力相对较弱;二受长宽比的影响,截面不同区域内部混凝土受到约束的程度不同.因此,在矩形薄壁钢管混凝土短柱极限承载力计算中做如下假设:

(1)外侧钢管屈服满足Mises条件,在极限状态时,有环向应力,其纵向承载力小于fyAs;

(2)内侧混凝土受到外侧钢板约束,处于三轴应力状态,但截面存在有效约束区和弱约束区,见图5所示.

3.2 有效约束区的简化

假设核心混凝土的有效约束区的边界线为二次函数为

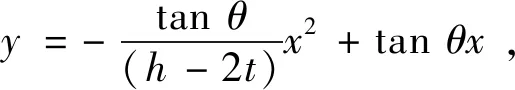
(1)

式中:钢板厚度为t;边界线在矩形截面角部的切线角为θ,MANDER等[17]建议对矩形钢筋混凝土柱取θ=45°.矩形薄壁钢管混凝土短柱轴压试件的有效约束区如图5所示.

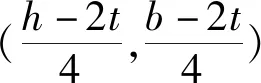
3.3 短柱轴压承载力计算表达式

根据简化计算分析方法,将柱横截面划分为3个部分:有效约束区的混凝土、弱约束区的混凝土以及钢管.建议矩形薄壁钢管混凝土短柱轴压承载力表达式为

Nu=αfcAcc+βfcAco+γfyAs,

(2)

式中:fc为混凝土的轴心抗压强度;Acc为简化计算分析方法中有效约束区混凝土面积;Aco为简化计算分析方法中弱约束区混凝土面积;fy为钢材的屈服强度;As为钢材的横截面面积.α为三轴受压状态下混凝土强度提高系数,β为弱约束区混凝土强度提高系数,γ为极限状态时钢管竖向承载力的折减系数.

有效约束区的混凝土受到侧向压应力约束作用的强度为

fcc=fc+4σ,

(3)

式中:fcc为简化计算分析方法中有效约束区混凝土的抗压强度,σ为矩形薄壁钢管对核心混凝土的等效侧向约束应力.

MANDER等[17]提出的矩形箍筋约束混凝土等效侧向约束应力在矩形薄壁钢管混凝土试件上同样适用,因此矩形薄壁钢管对核心混凝土的等效侧向约束应力σ:

σ=keσl,

(4)

其中:

(5)

式中:σl为矩形薄壁钢管对核心混凝土的侧向应力;ke为有效约束系数[17-18],Acc为有效约束区混凝土面积,Ac为横截面混凝土总面积.假定σl沿钢管内壁均匀分布,设σs为钢管的环向应力,如图7.

由力的平衡得:

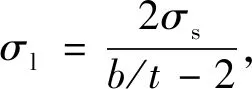
(6)

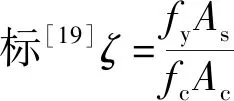
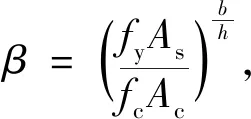
(7)

最后通过试验数据回归分析得γ=0.93.所以结合上述分析,矩形钢管混凝土短柱轴压承载力公式为

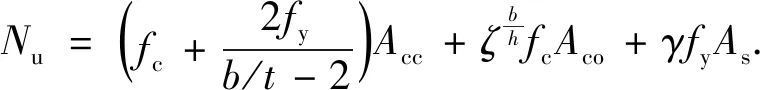
(8)

3.4 公式校核

为验证本文推导的矩形薄壁钢管混凝土短柱轴压承载力计算公式的正确性,按照公式(8)对本试验的32个试件进行计算,计算结果与试验结果的比较见图8.分析可得,试验结果与本文公式结果比值的平均值为1.06,标准差为0.047.极限承载力简化计算公式与试验结果吻合良好,能较为合理地评估矩形钢管混凝土柱的轴压承载力.

4 结 论

(1)矩形薄壁钢管混土短柱轴压破坏过程分为3个阶段:弹性工作阶段、弹塑性工作阶段、下降工作阶段.在弹性阶段薄壁钢管对混凝土的套箍作用弱,二者共同承受轴向荷载;在弹塑性阶段以及下降阶段,核心混凝土横向变形明显,此时薄壁钢管由承受轴向压应力为主变为承受环向拉应力为主,由钢管对核心混凝土提供环向约束,薄壁钢管短边方向约束强、长边方向约束弱.达到极限承载力之后,薄壁钢管屈曲明显且容易断裂,承载力开始下降,但相比无约束试件下降段平缓.

(2)矩形薄壁钢管混凝土轴心受压短柱的强度比、轴压刚度、承载力下降幅度与试件的长宽比有关.长宽比越大,强度比越小,轴压刚度越小,承载力的下降幅度越大.

(3)考虑矩形薄壁钢管混凝土短柱试件长边对核心混凝土的约束作用弱,短边的约束作用强.提出一种矩形薄壁钢管混凝土短柱轴压承载力简化计算分析方法,将核心混凝土的有效约束区进行简化,将试件分为3个部分:核心约束区的混凝土、弱约束区的混凝土和钢管.应用该方法对32根矩形薄壁钢管混凝土短柱轴压试件的承载力进行计算.结果表明,本文提出的极限承载力简化计算公式能较为合理地评估矩形薄壁钢管混凝土短柱试件的轴压承载能力.