一类欧拉-拉格朗日系统的自适应切换跟踪控制

邵渝琪,李 健,吴昭景

(烟台大学数学与信息科学学院,山东 烟台264005)

在实际工业生产过程中,许多机械系统都可以用欧拉-拉格朗日方程进行描述,例如,机器人[1-3]、船舶[4-5]、飞艇[6-7]、人造卫星[8-9]等.一方面,为了实现具体的工业生产目标,需要对机械系统施加相应的控制.另一方面,随着生产过程的复杂化,许多机械系统呈现出一些新的复杂特性(例如强不确定性、耦合性等),导致欧拉-拉格朗日系统的许多控制问题难以用现有方法解决,需要发展新的控制理论与方法.因此,对欧拉-拉格朗日系统控制问题的研究具有重要的理论意义和实际应用价值.

在过去的20年间,欧拉-拉格朗日系统的控制一直都是控制理论和控制工程研究的热点[10-16].针对具有不同物理背景的欧拉-拉格朗日系统,多类控制问题得到了解决,涌现出多种控制设计方法.如下主要从跟踪控制和镇定控制两个方面具体介绍:1)跟踪控制[10-13].文献[10]利用无源协调控制方法解决了多艘船舶的协调路径跟踪问题,文献[11]通过对未测量状态的非线性化部分施加单调阻尼条件的方法,解决了一类非线性耗散负载作用下欧拉-拉格朗日系统的输出反馈跟踪控制问题,文献[12]利用反馈线性化技术解决了倒立摆的跟踪控制问题,文献[13]研究了由多个相同欧拉-拉格朗日系统构成的网络系统的轨迹跟踪和同步控制问题.2)镇定控制[14-16].文献[14]利用势能整形方法研究了一类欧拉-拉格朗日系统的全局镇定问题,文献[15]通过无源性方法解决了一类欧拉-拉格朗日系统的全局输出反馈镇定问题,文献[16]通过无源性和能量整形方法解决了双倒立摆系统的全局镇定问题.需要指出的是,上述文献均假设系统不存在不确定性,即参数已知且不受外部扰动影响,这限制了结果的应用范围.然而,在实际控制过程中,受测量设备精度、建模方法局限性以及外部环境的影响,被控系统不可避免地存在不确定性(即参数未知或受外部扰动影响).不确定性的存在将导致上述针对确定系统的控制设计方法无效.因此,研究不确定欧拉-拉格朗日系统的控制问题具有重要意义.

实际上,不确定欧拉-拉格朗日系统的控制问题已经得到研究[17-24].具体地,当系统受不同类型外部扰动影响时,文献[17]和[18-19]分别研究了含有白噪声的随机欧拉-拉格朗日系统的最优控制和跟踪控制问题,文献[20-21]研究了含有有色噪声的随机欧拉-拉格朗日系统的跟踪控制问题,文献[22]研究了具有非随机扰动的全状态约束下不确定N连杆机器人的跟踪控制问题.当系统含有未知参数时,文献[23-24]研究了欧拉-拉格朗日系统的分布式跟踪控制问题.然而在实际工业生产过程中,许多受控系统的扰动具有一定的周期性和有界性,且周期和上界难以精确获得.未知周期和上界的存在导致上述文献中扰动补偿无效,需要发展新的扰动补偿机制,进而给出控制设计的新方法.

本文研究具有周期扰动的欧拉-拉格朗日系统的跟踪控制问题.由于扰动具有未知的周期和上界,故无法使用现有的控制设计方法.受相关文献启发[25-27],利用学习机制和切换机制,给出扰动不确定性的补偿机制.然后,利用反推控制设计方法,给出状态反馈控制器的显式形式.通过在线调节切换参数,使得所设计的控制器能够保证闭环系统所有状态均有界,并且系统输出跟踪到给定的参考信号.需要指出的是,文献[25]和[27]主要结果是针对由一阶常微分方程刻画的标量系统.与之不同的是,系统(1)是由二阶常微分方程刻画的向量系统.系统形式的显著不同将导致文献中的控制设计方法不能平凡地解决系统(1)的控制问题,将在控制器设计和切换机制构建等方面产生新的困难.特别地,文献[25]和[27]的控制设计方法无法应用.为此,本文通过引入向量型反推设计方法给出控制器的显式形式.

1 问题描述

考虑一类具有未知周期扰动的欧拉-拉格朗日系统

(1)

如下给出系统(1)2个重要的性质[28],将应用于控制器设计和稳定性分析中.

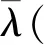
其中,In×n表示n×n维单位矩阵.

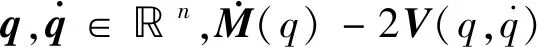
为确保控制目标的实现,给出如下假设.

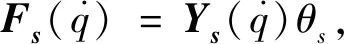
假设2 扰动ξ(t)是有界的周期的,最小正周期T*可以表示为T*=l*τ,其中,τ是已知常数,l*是未知整数.μ*是ξ(t)的未知上界.

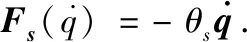
2 基于切换机制的反推控制器设计

2.1反推控制器的设计

为了方便应用反推设计步骤,将系统(1)改写成如下形式

(2)

对上述系统,引入如下状态变换

(3)

其中,α为待定光滑函数.对式(3)两边分别求导并利用式(2),得到如下误差系统

(4)

进而,通过式(2)和式(4)可以得到

(5)

如下通过两步反推设计步骤,给出系统(2)控制器设计的详细过程.

第1步选取类Lyapunov函数

其中,kp为正常数.沿误差系统(4)的解,求得V1的导数为

通过选取α(q,q*)=-c1z1,上式转化为

(6)

其中,c1>0为待设计的参数.

第2步假设T和μ分别表示扰动ξ(t)的周期和上界,进而选取类Lyapunov函数

(7)

sgn(·)为符号函数.需指出的是,上述饱和函数具有如下重要性质[26]:

(ξi-ξj)2≥(satμi(ξi)-satμi(ξj))2.

∀|ξi|≤μi,ξj∈1,i,j=1,2,…,n.

利用上述性质及式(5)、(6),可得

(8)

为了保证式(8)右端负半定,选取如下控制器

其中,c2>0为控制器参数.利用上式及性质2,式(8)转化为

-kpc1|z1|2-c2|z2|2-

-kpc1|z1|2-c2|z2|2+

(10)

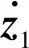
需指出的是,由于扰动ξ(t)的周期和上界均是未知的,所以控制器参数T和μ无法确定,导致上述学习控制器(9)无法实施.为此,将在下一节给出控制器参数T和μ的在线调节机制,保证控制器的可实施性,从而实现拟定的控制目标.

2.2 切换机制的建立

设定初值:

*预选2个正数c3和c4.

切换逻辑：在任一时刻t>ts,如果满足

|z1(t)|2+|z2(t)|2≥M1

或

或

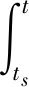
3 闭环系统稳定性分析

定理1 考虑满足假设条件1,2的欧拉-拉格朗日系统(1).自适应学习控制器(9)在2.2节给出的切换机制下保证闭环系统所有状态都有界,并且输出信号q(t)跟踪到给定的参考信号q*(t),即

证明定理证明分成两步.首先利用反证法证明切换仅发生有限次,然后证明切换仅发生有限次时,所有闭环系统状态有界且输出跟踪到给定的参考信号.

第1步假设发生无限次切换.则存在整数i*使得

(11)

mod(i*+1,l*)=0.

(12)

令ti*为第i*次切换时刻,ti*+1为下一切换时刻,则根据切换机制有

|z1(ti*+1)|2+|z2(ti*+1)|2≥M1

(13)

或

(14)

或

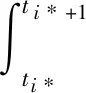
(15)

(16)

(17)

此外,利用性质1及式(11)并由M1的定义可得

利用上式及式(16),(17),可得到

2(i*+1)c4+2M1=M2,

上述三式显然与式(13),(14),(15)矛盾.因此,只有有限次切换发生.

第2步假设tif为最后一次切换时刻,则对所有的t>tif,根据切换逻辑有

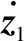
4 仿真算例

本节以图1所示的非线性基准系统[20]为例进行仿真实验,验证理论结果的有效性.与文献[20]不同的是,本文研究的系统所受扰动是非随机的,且带有未知的周期和上界.此外,还考虑了空气阻力对系统产生的影响.系统相关系数矩阵给定如下:

5 结 论

本文解决了一类受扰动欧拉-拉格朗日系统的跟踪控制问题.与相关文献不同的是,系统所受扰动是非随机的,并且具有未知周期和上界.这导致相关文献的方法不能应用.通过结合反推控制设计方法和扰动学习、切换机制,给出了系统自适应切换控制设计方法.通过在线调节切换参数,所设计的控制器保证了闭环系统所有状态都有界,并且系统输出跟踪到给定的参考信号.需指出的是,本文所设计的控制器要求系统全部状态可量测,在实际应用上具有一定程度的限制.因此,如何在较少量测信息下实现系统的跟踪控制目标,提高控制器的应用性具有重要的意义.为此,需要利用可量测的系统输出设计恰当的状态观测器重构系统不可测状态.这将使得该类系统的跟踪控制更具有挑战性.