多车型冷链物流配送车辆的路径优化

孙国华，屈冉冉

(1.山东财经大学 管理科学与工程学院，山东 济南 250014；2.天津大学 管理与经济学部，天津 300072)

一、引言

冷链物流是使货物始终处于规定低温环境下，保持货物品质、减少货物损耗的一种快速物流模式[1]。近年来，我国冷链物流发展迅速，2018 年冷链物流市场规模近3 000 亿元，预计2020 年将达到4 700 亿元，复合增速达21.5%[2]。作为冷链物流的一个重要环节，冷链物流配送被认为是物流行业中的“最后一块蛋糕”。通过科学合理的优化冷链物流配送车辆路径，可以实现降低配送成本，保证冷链产品质量，提高客户满意度的目标，因此，研究冷链物流配送车辆路径优化问题具有十分重要的实践价值。

冷链物流配送是近年来的一个研究热点，研究主要集中在考虑配送时间或者客户满意度的单车型冷链物流配送车辆路径优化问题。Hsu 和Chen[3]针对不同温度要求的食品，研究了车队规模与配送调度优化问题。Govindan 等[4]研究了易腐品供应链网络中带有时间窗的选址—车辆路径优化问题。Yu 等[5]研究了易腐食品冷链配送问题，以成本最低及满足客户对各种食品的预先质量要求为目标，对冷链食品的配送问题进行了优化建模。Zhang 和Chen[6]以最小化运输成本为目标，研究了多种不同特性冷冻食品的共同配送问题。Song和Ko[7]针对易腐食品的城市配送问题，建立了非线性规划模型并设计了启发式算法。吴瑶和马祖军[8]对时变路网环境下带时间窗的易腐品生产—配送集成调度问题进行了研究，建立了混合整数规划模型，并采用混合遗传算法进行了求解。丁秋雷等[9]建立了鲜活农产品冷链物流配送的干扰管理模型，并采用混合蚁群算法进行求解，生成了使系统扰动较小的调整调度方案。以上研究通常假设采用单一车型的车辆提供配送服务，这与实际中企业通常采用多种不同车型的车辆提供配送服务具有一定的差距。因此，已有研究并不完全适用于解决实际中的多车型冷链物流配送车辆路径优化问题。

目前，有关多车型混合车辆路径问题的研究已有很多成果，Brandao[10]运用禁忌搜索算法研究了多车型车辆路径优化问题。Penna 等[11]在迭代局部搜索算法中引入了变邻域下降搜索程序与随机邻域排序，并用于解决多车型车辆路径优化问题。Leung 等[12]运用带有局部搜索的模拟退火方法，求解了装载空间具有二维装载约束的多车型车辆路径优化问题。Kopfer 等[13]研究了碳排放量最小的多车型车辆路径问题，发现采用混合车型进行配送可以极大地降低碳排放量。Dominik 和Michael[14]考虑了电动商用车和传统燃油车共存的多车型车辆路径优化问题。潘雯雯等[15]研究了需求可拆分的多车型车辆路径优化问题，提出了路径优化和路径改进相结合的两阶段算法，对建立的混合整数规划模型进行了求解。田宇等[16]对集送货一体化的多车型车辆路径问题进行了研究，并提出了一种基于多属性标签的蚁群算法。上述研究主要针对常温商品的配送，而生鲜产品的配送具有很强的时效性，因此上述研究并不完全适用于解决冷链物流配送车辆路径优化问题。

针对冷链物流配送车辆路径优化问题，本文将在考虑多种车型共存的前提下，构建整数规划模型，设计基于大车优先原则和满载优先原则的遗传算法对模型进行求解，并采用实验数据与仿真实例验证算法的有效性。

二、模型构建

(一) 问题描述

某冷链物流公司拥有一个配送中心和多种车型(载重量和运输成本不同)的车辆，并负责向区域内若干客户配送生鲜产品。配送车辆的最大载重量和配送时限已知，配送中心和客户的地理位置、客户的需求量确定。配送优化目标为：合理安排车辆配送路径，在保证满足车载容量约束、车辆数约束及车辆行驶时间约束的前提下，使得总配送费用最小。

(二)模型假设

1.配送中心库存量可满足所有客户需求；

2.配送中心有K种车型的冷藏车，车辆数足够完成配送任务，且车载容量大于单个客户的需求量；

3.车辆从配送中心出发，完成配送任务后返回配送中心；

4.由于生鲜产品具有很强的时效性，车辆必须在规定时限内完成配送任务；

5.客户需求不可分割，每个客户需被一辆车服务，且只能被服务一次。

(三)模型符号

1.标号

i，j：节点标号；

n：客户的个数；

k：表示第k种车型的车辆；

l：表示第k种车型的第l辆车。

2.模型使用参数

G ＝(V，A，D) ：冷链物流配送网络；

V ＝{0 }∪Vc：节点集，其中0 代表配送中心，Vc ＝{1，...，n} 为客户点集；

A ＝{(i，j)｜i，j∈V，i≠j} ：有向弧；

K：车辆类型集；

dij：节点i到j的距离，i，j∈V；

Lk ＝{1，2，...，Mk} ：第k种车型的车辆集合，其中Mk为第k种车型的车辆数；

ck：第k种车型车辆的单位运输成本；

fk：第k种车型车辆的固定成本，主要包括驾驶员的工资成本和车辆折旧成本；

Qk：第k种车型车辆的车载容量；

qi：客户i的需求量；

tij：节点i到j的行驶时间；

si：客户i需要的服务时间；

T：车辆运行时间上限；

：节点i在车辆k行驶路径中的位势。

3.决策变量

(四)多车型冷链物流配送车辆路径优化模型构建

由以上的问题描述和假设条件，构建以运输成本最低为目标的冷链物流配送车辆路径优化模型，具体如下：

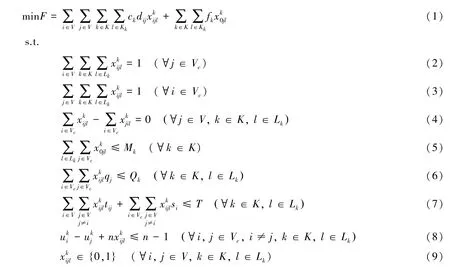
公式(1)为目标函数，表示最小化总配送成本，其中第一部分是可变运输成本，第二部分是车辆的固定成本；式(2)和式(3)保证每个客户均被某种车型的某辆车服务一次；式(4)保证驶入客户j与驶出客户点j的是同一辆车；式(5)保证每种车型的使用数量不大于该种车型的车辆总数Mk；式(6)保证每辆车不违反车载容量约束；式(7)保证配送车辆在规定时间内完成配送任务；式(8)保证配送路径中不包含子回路；式(9)定义了变量的取值范围。

三、算法设计

车辆路径问题是经典的NP-hard 问题，运用精确算法无法在较短时间内得到最优解，因此有必要采用智能算法对所研究的问题进行求解。由于冷链物流配送系统存在多种车型，首先需要解决的问题就是车型选择问题。从减少车辆数降低车辆固定成本的角度，应该优先使用大车；从提高车辆利用率的角度，应该优先考虑车辆满载。因此，本文提出了大车优先和满载优先两种原则，并与遗传算法相结合对所研究的问题进行了求解。

大车优先原则：在安排车辆时，依据车载容量的大小，优先给车载容量大的车辆分配任务，在所有大车均被分配配送任务后，再考虑给车载容量小的车辆分配任务。这样做的好处是可以减少配送车辆数，降低车辆固定成本，容易实现配送的规模经济。

满载优先原则：在安排车辆时，依据客户累积需求量的大小，优先将相应的客户分配给满载率高的车型。这样做的好处是提高了车辆利用率，减少了车辆的空驶距离。

(一)编码与解码

采用基于客户直接排序的自然数编码方式编码，将配送中心设定为编号0，各个客户按照1，2，…，n进行编号，自然数的排列顺序表示车辆访问客户的顺序。popsize ＝N表示种群中有N个个体。

基于大车优先的解码机制：针对每一个后代，在不违反车辆行驶时间的前提下，依据排序对客户的需求量进行累加，优先考虑是否违反未安排任务的大车的车载容量限制，如果不违反，则将客户分配给相应的大车服务，否则，重新累加，并将客户安排给车载容量小的车辆服务。重复该步骤，直至所有的客户都被纳入车辆路径中。

基于满载优先的解码机制：针对每一个后代，在不违反车辆行驶时间的前提下，依据排序对客户的需求量进行累加，优先考虑是否达到某种车型车辆车载容量的P比例(P∈[0.95，1])，如果该车型有车辆未被安排配送任务，则停止累加，并将客户分配给相应的车辆服务；否则，继续累加；重复该步骤，直至所有客户被纳入车辆路径中。

(二)适应度函数设计

由于多车型冷链物流配送车辆路径优化问题以总配送费用最小为目标函数，因此取fitness ＝为适应度函数，利用其评价个体的好坏。适用度越高，说明总配送费用越小，对应的个体越好。

(三)遗传算子的设计

1.选择算子

采用适应度比例方法对个体进行选择，淘汰率为Ps。淘汰适应度较小的个体，适应度较高的个体则直接复制到下一代，这样可以减少算法的操作个数，提高总体的运算速度。

2.交叉算子

采用部分匹配交叉策略PMX 完成交叉操作。

(1)根据均匀随机分布产生两个基因交叉点，定义这两点之间区域为一匹配区域，如A＝3 4 6 ｜8 1 2 ｜9 7 5，B ＝2 7 1 ｜9 5 3 ｜6 4 8。

(2)使用位置交换操作交换两个父串的匹配区域，得到：A1＝3 4 6 ｜9 5 3 ｜9 7 5，B1＝2 7 1 ｜8 1 2 ｜6 4 8。

(3)对于A1和B1两个子串中匹配区域以外出现的重复节点，依据匹配区域内位置映射关系进行逐一交换。对A1匹配区域以外的9、5、3 分别以8、1、2 替换得：A2＝2 4 6 ｜9 5 3 ｜8 7 1，同理，B2＝3 7 5 ｜8 1 2 ｜6 4 9。

3.变异算子

个体采用对调变异策略，通过在个体中随机选取两个变异点，将两点的基因值进行交换，其中个体变异的概率为Pm。

(四)终止准则

采用进化代数gen ＝T作为循环迭代终止的条件，如果gen ＞T则算法结束，输出适应度值最高的解，否则，重复上述过程。

(五)算法步骤

遗传算法步骤如图1 所示：

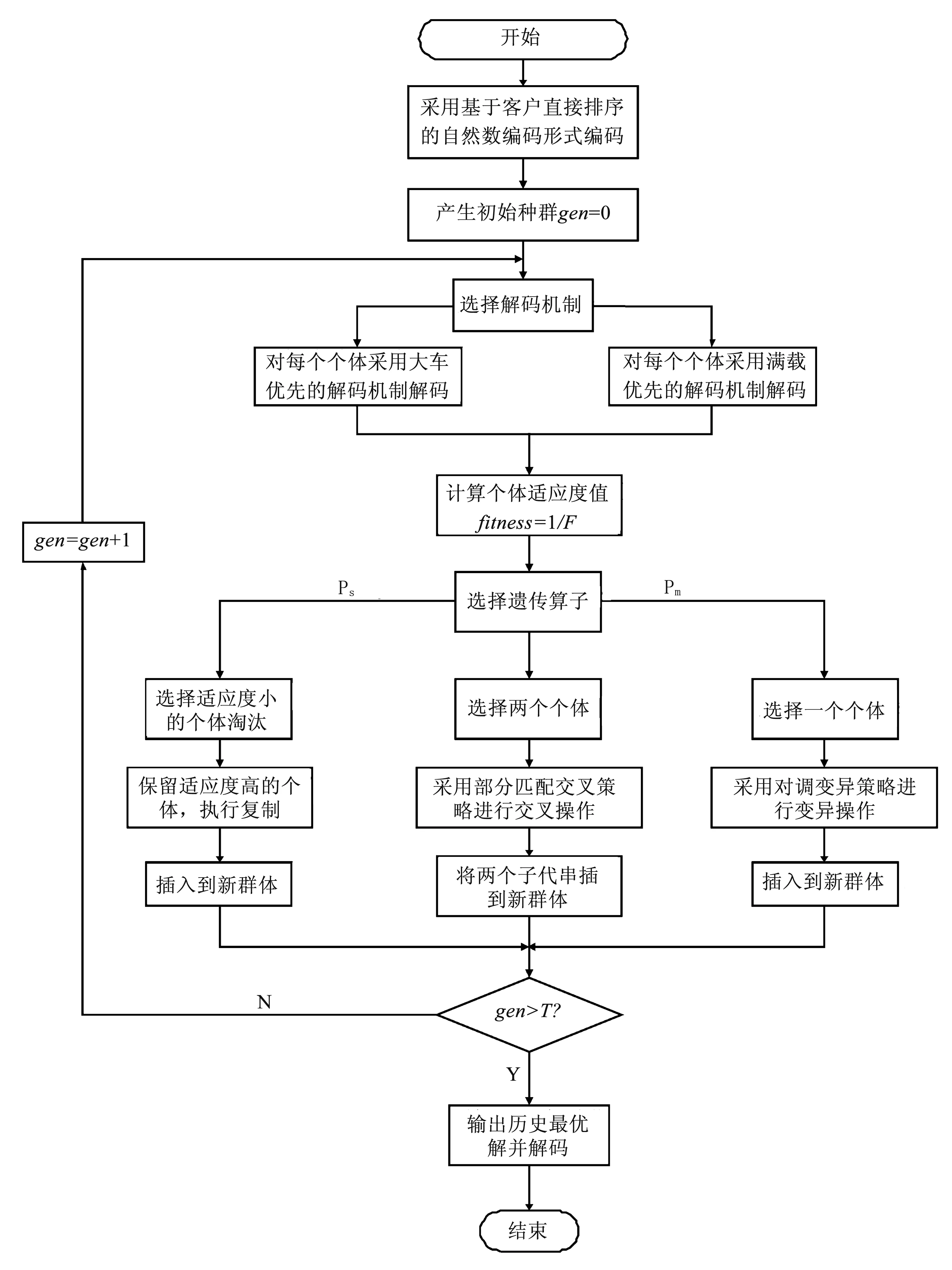
图1 遗传算法步骤

四、实验仿真

(一)数值实验

为了验证算法的有效性，通过随机生成的算例进行了实验仿真，在Intel(R)Core(TM)i5-6200U 2.30GHZ CPU，4GB RAM 和64 位Windows 7 操作系统的机器上，针对规模为5～9 的冷链物流配送车辆路径优化问题，随机生成客户及配送中心的距离矩阵，并采用本文设计的算法各运行了10 次。

在数值算例中，配送中心有两种车型，其固定成本分别为f1和f2。其中，遗传算法参数设置为：popsize ＝150，gen＝500，Ps＝0.2，Pm＝0.3。

仿真结果由表1 和表2 所示，其中表1 给出了每种算法的平均计算时间，表2 给出了每种算法同精确算法相比的平均相对误差(相对误差＝绝对误差/最优值×100%)。

表1 算法的平均计算时间 单位：秒

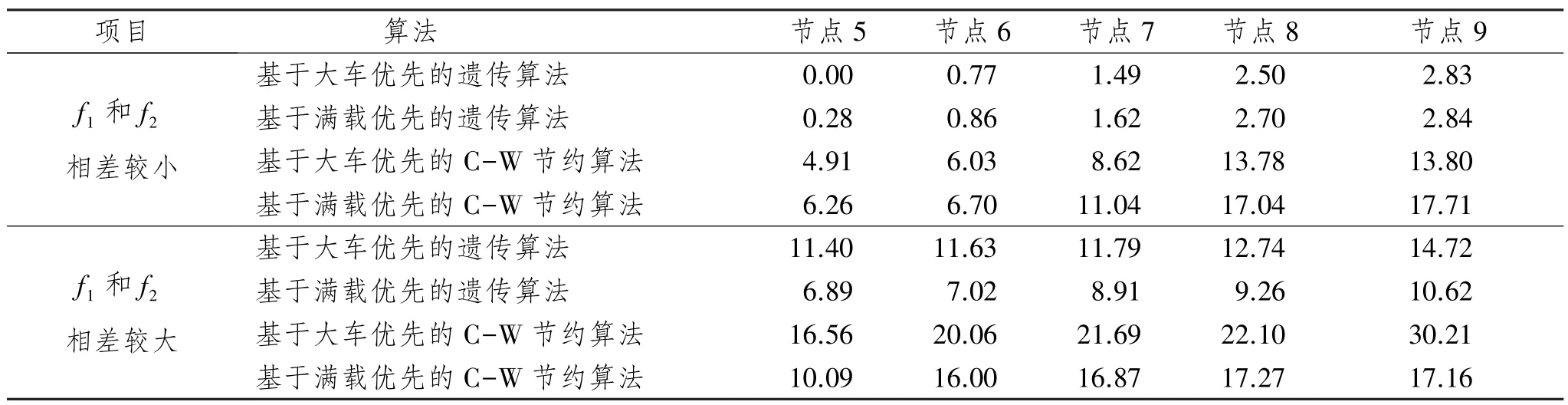
表2 平均相对误差

由表1 可以看出，随着节点规模的增大，精确算法所需的计算时间急剧增加，当节点数为9 时，精确算法的计算时间已经超过30 分钟，而C-W 节约算法与遗传算法都可以在较短时间内求得较优解。由表2 可以看出，不论是基于大车优先还是满载优先的原则，遗传算法求解的解整体优于C-W 节约算法求解的解。进一步分析发现，基于大车优先原则与基于满载优先原则在不同情形下各具优势。当不同车型的车辆固定成本相差较小时，基于大车优先原则的算法求出的结果平均相对误差较小，即大车优先原则较优；当不同车型的车辆固定成本相差较大时，基于满载优先原则的算法求得的结果相对误差较小，即满载优先原则较优。说明大车优先原则适用于不同车型车辆固定成本相差较小的情形，满载优先原则适用于不同车型车辆固定成本相差较大的情形。

(二)H 物流公司仿真实例

为了进一步验证算法的有效性，利用本文设计的算法对H 冷链物流公司的实际问题进行了求解。

1.基本数据

H 冷链物流公司是位于B 市的一家第三方冷链物流公司，占地约5 600 平方米，主要为市内的37 家便利店提供冷链物流配送服务。目前，公司自有4.2 米与3.5 米两种车型的厢式冷藏货车负责配送，两种车型在市区内平均运行速度均为30 千米/小时；车辆晚上11 点出发开始执行配送任务，次日凌晨7 点完成配送任务返回配送中心。

配送中心和客户的位置如图2 所示(其中H 处为H 物流公司位置，其他标记为便利店位置)。

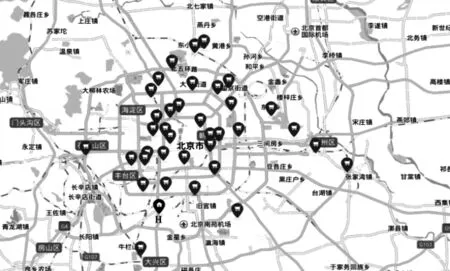
图2 配送中心和客户位置分布

车辆信息如表3 所示。

表3 车辆信息

配送中心编号为0，其位置经纬度为(116.354 667，39.817 295)。部分客户的位置、订单需求量、服务时间等信息如表4 所示(客户从1 开始编号)。

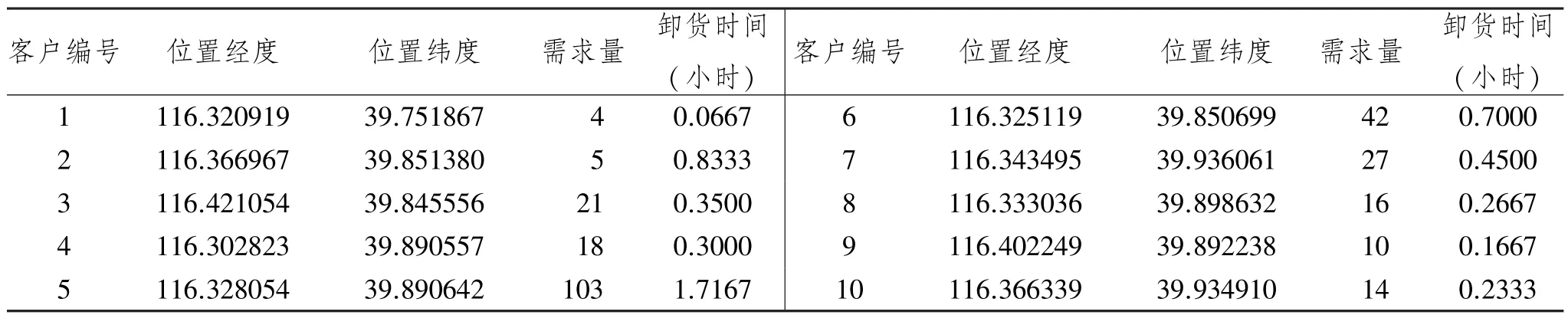
表4 部分客户数据

2.车辆路径优化方案

基于上述数据，采用本文设计的算法进行了求解，具体配送路线如图3～图6 所示，不同配送方案的总费用如表5 所示。

从图3～图6 可以看出，基于大车优先的C-W 节约算法得到的配送方案共使用6 辆A 型冷藏车进行配送服务，基于满载优先的C-W 节约算法得到的调度方案共使用7 辆车进行配送，其中4 辆A 型车，3 辆B 型车。基于大车优先的遗传算法在第476 代求得最优解，求得的方案需要5 辆A 型车；满载优先的遗传算法在第486 代求得最优解，求得的方案需要7 辆车进行配送，其中3 条路线由A 型车配送，4 条路线由B 型车配送。不难看出，基于大车优先原则的C-W 节约算法和遗传算法求得的配送方案分别比基于满载优先原则的C-W 节约算法及遗传算法需要的车辆更少且费用较少。对比四个方案的运输费用可以看到，不论是基于大车优先还是满载优先的原则，遗传算法求解的解整体优于C-W 节约算法求解的解。因此，针对这个实例，遗传算法求得的配送方案结果更优。

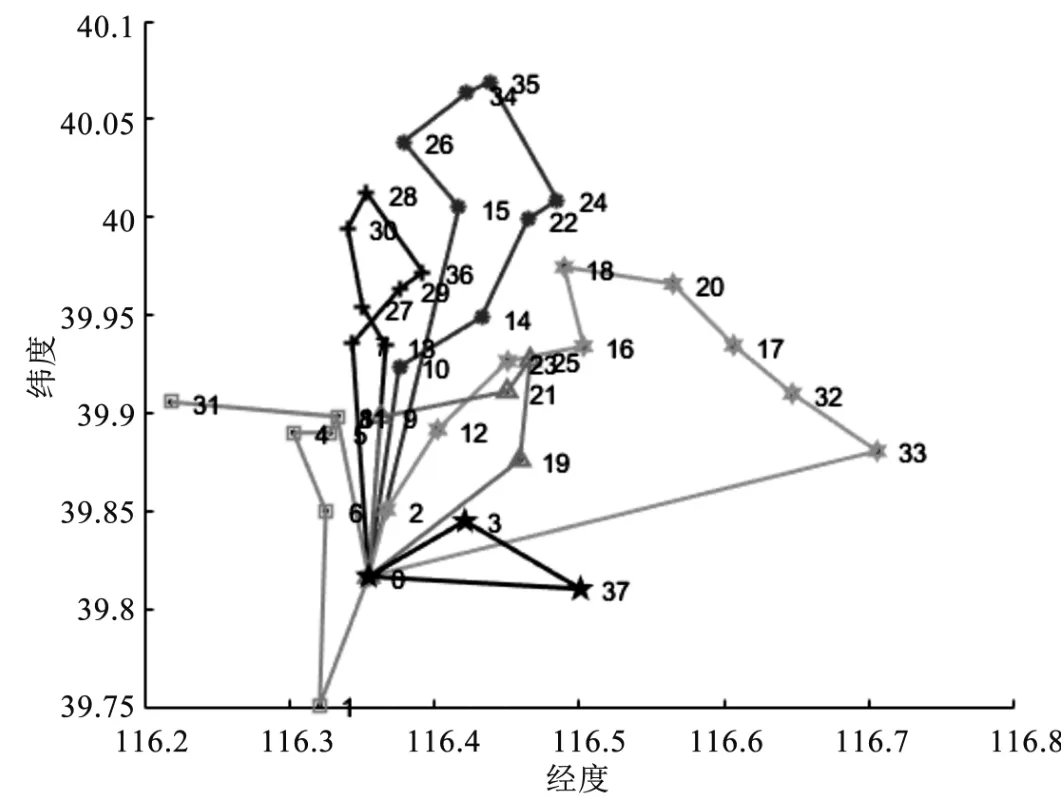
图3 基于大车优先的C-W 节约算法生成的配送线路

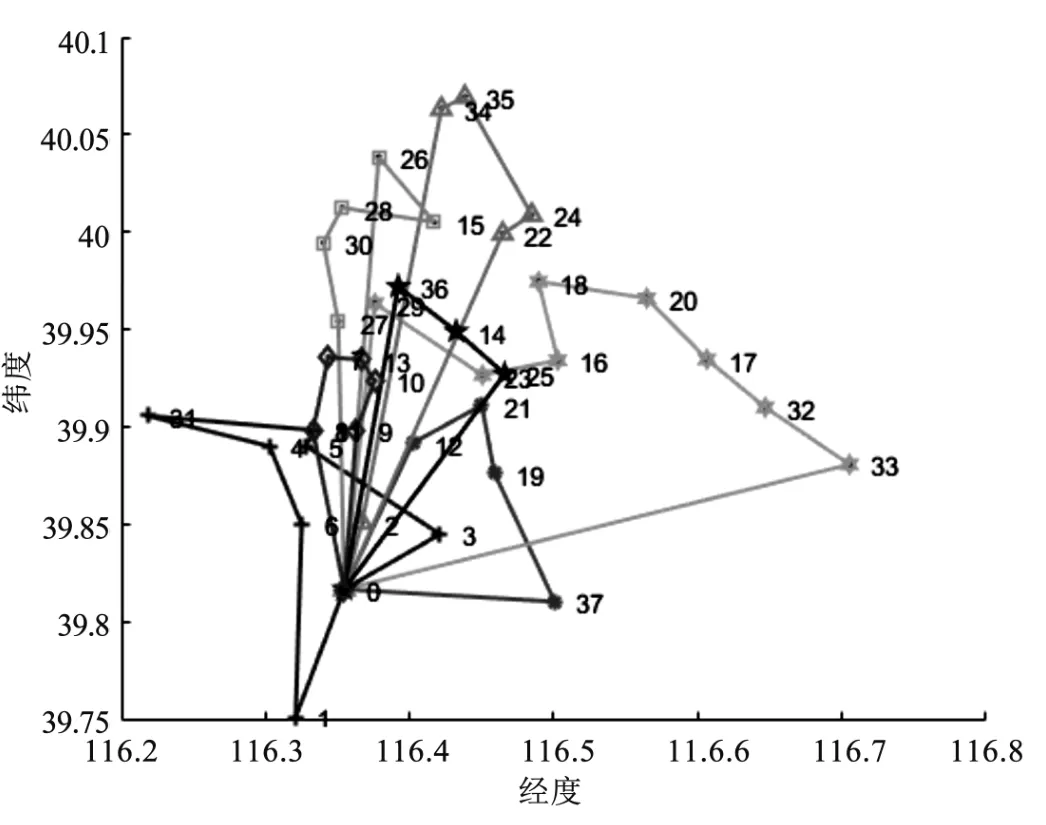
图4 基于满载优先的C-W 节约算法生成的配送线路

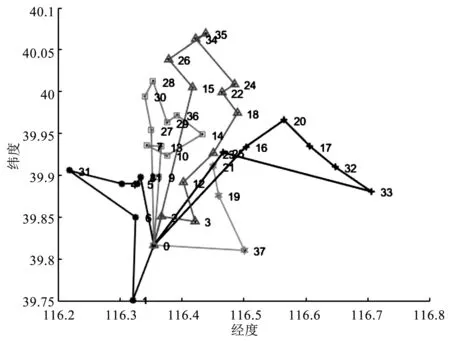
图5 基于大车优先的遗传算法生成的配送线路

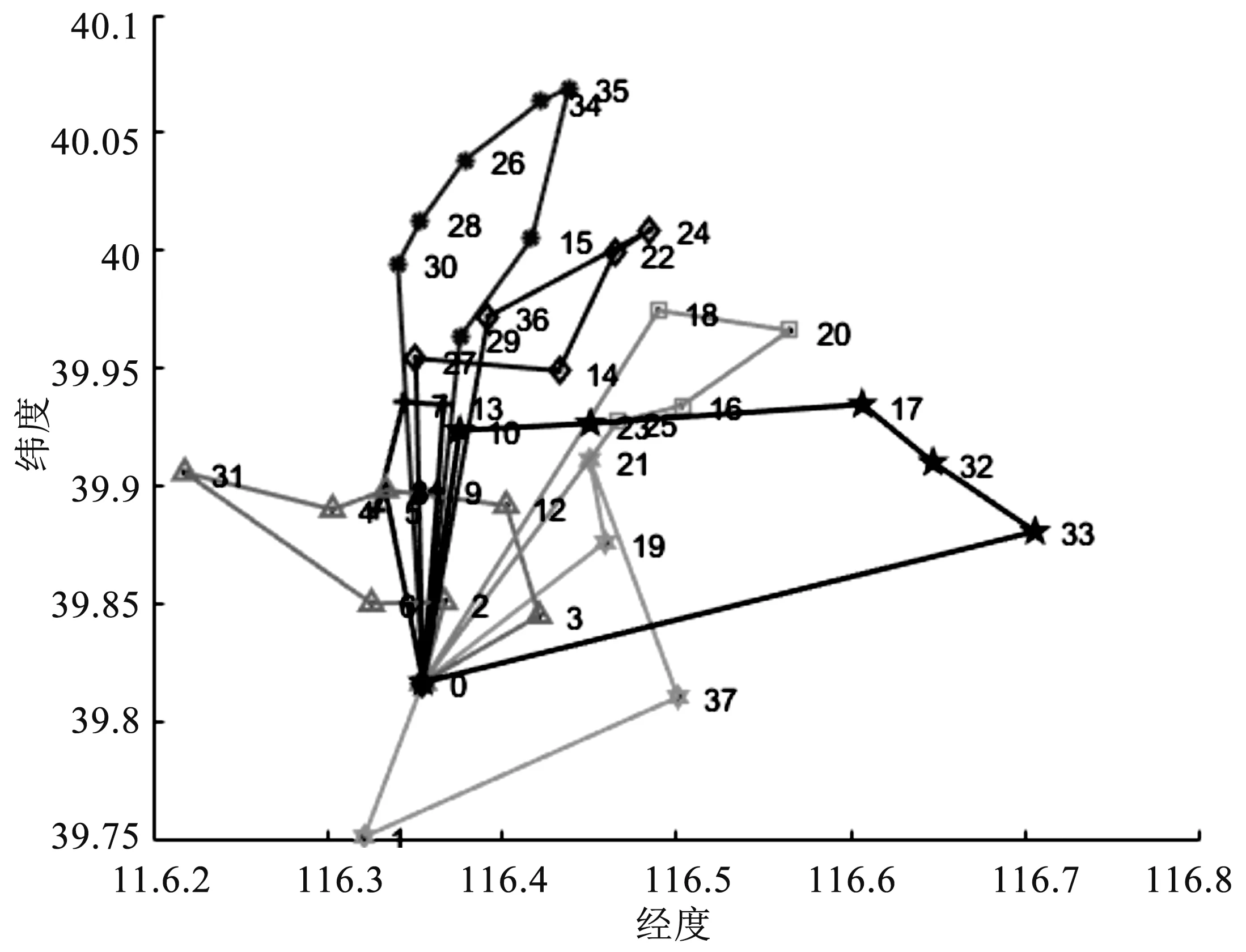
图6 基于满载优先的C-W 节约算法生成的配送线路

表5 总运输费用 单位：元

五、结论

本文针对冷链物流配送系统中存在多种车型的情形，构建了整数规划模型研究了冷链物流配送车辆路径优化问题。由于车辆路径问题为经典的NP-Hard 问题，精确算法无法在短时间内得到最优解，因此设计了基于大车优先原则和满载优先原则的遗传算法对所研究的问题进行求解。为了验证算法的有效性，采用实验数据与仿真实例对算法的有效性进行了验证，并与精确算法和基于大车优先与满载优先的C-W 节约算法进行了比较。研究发现：基于两种原则的遗传算法均可以在较短时间内得到可行解，而且相对C-W 节约算法，可行解的相对误差更小；当不同车型车辆固定成本相差较小时，基于大车优先原则的遗传算法所得配送方案更优，当不同车型车辆固定成本相差较大时，基于满载优先原则的遗传算法所得配送方案更优。最后，将提出的算法应用于H 冷链物流公司的实际配送中，发现基于大车优先原则和满载优先原则的遗传算法求得的配送方案比相应的C-W 节约算法求得的方案更优，进一步验证了提出的遗传算法的有效性。

本文研究的冷链物流配送车辆路径优化问题只考虑了配送时间限制，在今后的研究中将进一步考虑制冷成本、货损成本等因素对车辆路径的影响。