某新型船舶在海浪作用下的横摇运动分析∗

李 晨 陈永冰 李文魁 周 岗

（海军工程大学电气工程学院 武汉 430033）

1 引言

船舶在航行过程中不可避免会受到风浪等因素干扰，产生不同的运动，其中船舶的横摇运动对船舶的影响最大［1］。横摇会对船舶的正常航行、人员舒适度、以及船舶的使用寿命等产生很大的影响，严重情况下还会造成船毁人亡的巨大经济损失［2］。

减摇装置经过了漫长的发展历程，到目前主要的减摇方式有:舭龙骨、减摇水舱、减摇鳍、舵减摇等［3］，而其中减摇鳍、舵减摇以及舵鳍联合减摇领域的研究与应用最为热烈、最为广泛，舵减摇的探索与研究更是方兴未艾。与其它减摇技术相比，舵减摇技术凭借结构简单，费用低，效果好，灵敏性高等一系列优点，备受各国学者的追捧［4～7］。

本文通过建立的Matlab仿真平台，将该船的实际船体参数带入海浪干扰模型和船舶运动模型中，通过改变船舶航速、航向、海况来探究船舶航速、航向（与海浪形成遭遇角）以及不同海况下海浪对船舶横摇运动的影响规律，同时利用所得的变化规律仿真设计在恶劣环境下船舶产生的横摇运动，为船舶航行和减摇提供基础性研究。

2 船舶在海浪干扰下横摇模型

2.1 不规则波浪的描述

海浪是船舶在航行时受到的主要外界干扰，因此对海浪建立合适的干扰模型至关重要。

本文应用波能谱理论，将海浪看作是可以用足够多相互独立且具有随机的波幅和相位单元的规则波的叠加［8］。表达式如式（1）所示:

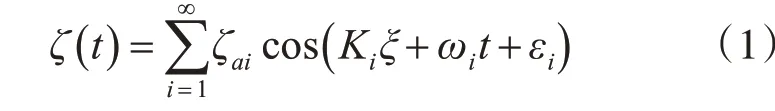
其中:ζai表示单元规则波的幅值，Ki为单元规则波的波数，ξ为海平面某一点的坐标，ωi表示单元规则波的频率，εi表示单元规则波的波相角。

当海浪在固定点时，海浪模型可以式（2）近似表达:

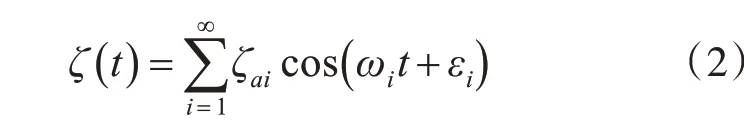
2.2 海浪波倾角仿真

海浪波倾角指的是海浪波形的切线与水平线之间的夹角［10］，表达式如式（3）:

本文借助“波能谱”来描述海浪，因此，在单位面积上的规则波所具有的波能可以用式（4）表示:

其中，ρ为海水密度，单位为kg/m3，g为重力加速度（g=9.8m/s2）。

根据叠加原理，在频率为[ ]ω，ω+dω内单元波所具备的波能为

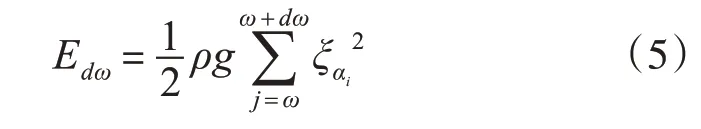
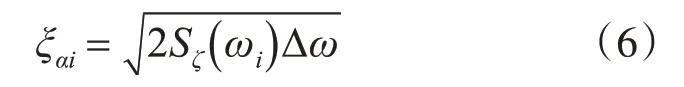
因此，波倾角的数学表达式用（7）表示:

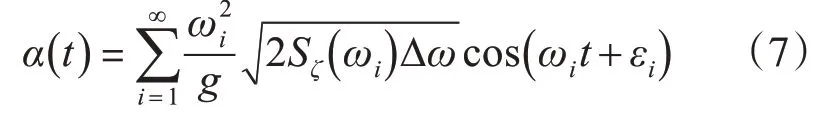
在实际应用中，还要考虑不同海况和船型以及船舶实际吃水影响，因此本文用有效波倾角αe(t)来替代α(t)。转换关系式如下:

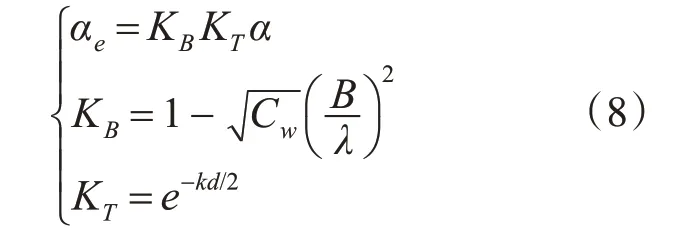
其中，λ为实际随机海浪的波长；Cw为水线面系数；d为船舶实际吃水深度。

波浪谱的形式有很多，比如常用的P-M 谱、双参数谱、方向谱、ITTC 单参数谱等［9］。本文采用P-M谱:

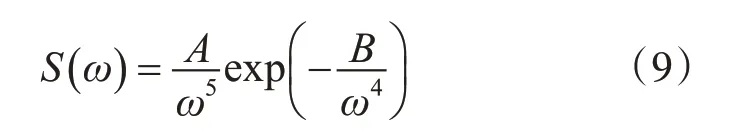
其中，A=8.11×10-3g2，B=3.11/(h1)2，h1为有义波高。在有义波高取不同数值时，波谱密度的变化如图1所示。

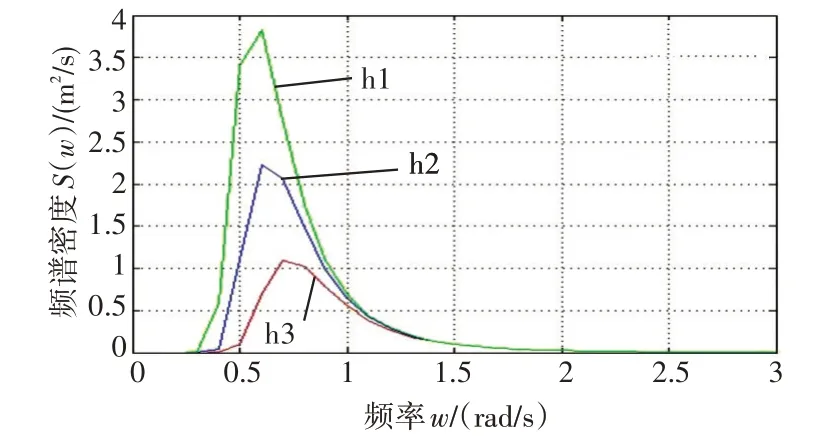
图1 海浪波谱密度曲线

2.3 遭遇角和遭遇频率

遭遇角又称波向角，是波浪的角度与船尾向的夹角，用μ表示。按照遭遇角μ不同，可以把海浪与船体的关系分为:迎浪，艏斜浪，横浪，艉斜浪和随浪［11］，如图2所示。

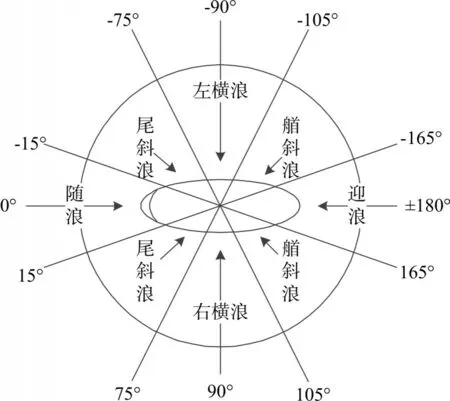
图2 遭遇角（μ）的定义

当船舶在水中航行时，船舶受到的海浪频率实际上是和船舶、海浪两者相关的遭遇频率ωe，而遭遇频率与海浪频率之间关系可以用式（10）表示:

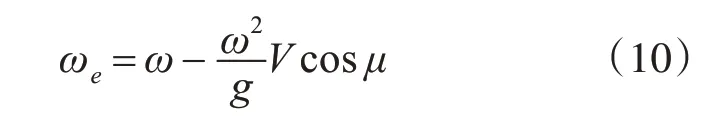
2.4 船舶横摇运动的受力分析

本文将船舶看作一个刚体，在海浪的作用下，船舶产生横摇［12］。本文用φ，φ˙，φ¨ 分别表示船舶横摇角、横摇角速度和横摇角加速度，单位分别为rad、rad/s和rad/s2。

和船舶横摇有关的力矩主要有:惯性力矩、阻尼力矩、恢复力矩和海浪干扰力矩［13］。因此本文着重从这三个影响因素出发，观察其对船舶横摇角的影响规律。

1）惯性力矩

由于横摇角加速度的存在，必然会产生对横摇轴的惯性力矩。其表达式为

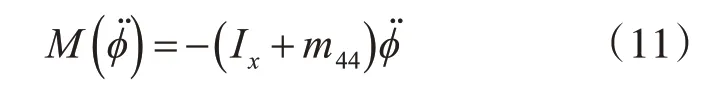
其中，Ix为船体绕X 轴的转动惯量，m44为船体绕X轴的附加转动惯量，单位为kg·m2。

2）阻尼力矩

船舶在水中发生横摇运动，由于此时船舶和水之间存在了相对速度，那么水必然产生对其的阻力，这就是阻尼力矩，用下式表示

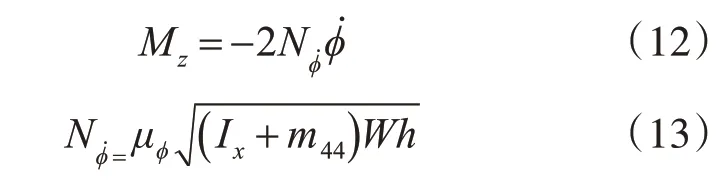
其中，Nφ˙为横摇阻尼系数；μφ为无因次横摇衰减系数；W为船舶排水量，单位为吨；h为初始横稳性高，单位为m。

3）复原力矩

当船舶横摇到某一角度时，由于重心和浮心不在同一条直线上，此时会产生一个使船舶回到原位置的恢复力矩，表达式如下:

4）海浪干扰力矩

海浪干扰力矩是引起船舶横摇运动的主要原因，它由以下三部分组成；

（1）船体的附加惯性扰动力矩:

（2）海浪对船舶航行时的阻尼扰动力矩:

（3）海浪改变船体水下部分体积的形状而产生的复原力矩:

2.5 船舶横摇运动建模

根据上述对船舶横摇运动的受力分析，可以得出船舶线性横摇运动的数学模型:

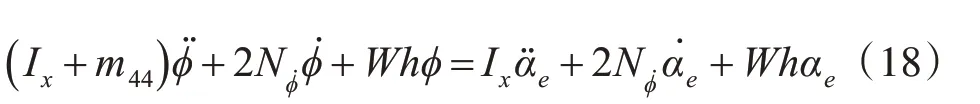
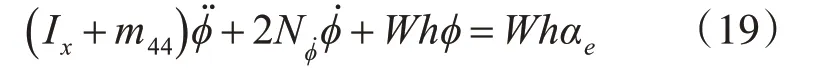
3 海浪造成船舶横摇运动的仿真分析

在建立的海浪干扰模型和船舶横摇运动模型基础上对该船舶进行仿真研究，通过改变船舶的航速、航向以及海况，探究在不同影响因素下船舶横摇角的变化规律。并且根据影响因素对船舶横摇角的影响规律，设计出船舶可能遇到的恶劣处境，仿真分析该船舶耐波性和安全性。

3.1 探究不同海况对船舶的横摇角影响

首先，不同海况下所选取的有义波高所对应如表1所示。

表1 不同海况下的有义波高选取表

实验中，本文在航速18 节下，遭遇角30°下，实验不同的海况，比较分析不同海况下，船舶横摇角变化，探究海况对船舶横摇角影响。

1）在航速18 节，遭遇角为30°，四级海况（取有义波高为2m）时，船舶的横摇角变化（如图3）。

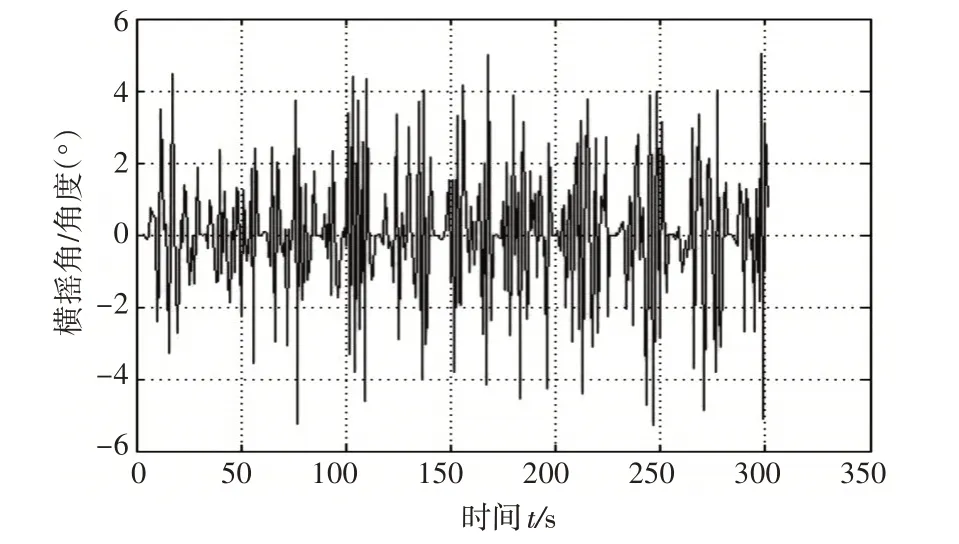
图3 在航速18节，遭遇角为30°，有义波高为2m时，横摇角的变化

2）在航速18 节，遭遇角为30°，五级海况（取有义波高为3.8m）时，船舶的横摇角变化（如图4）。

3）在航速18 节，遭遇角为30°，七级海况（取有义波高为7m）时，船舶的横摇角变化（如图5）。

根据仿真实验可得在航速18 节，遭遇角30°，不同海况下船舶横摇角的变化如表2。

对比图3、图4、图5，结合表2 可以看出，在船舶航速和遭遇角不变的情况下，海浪引起的船舶横摇角变化与海况有关，随着海况等级的升高、有义波高的增大，船舶横摇角增大。

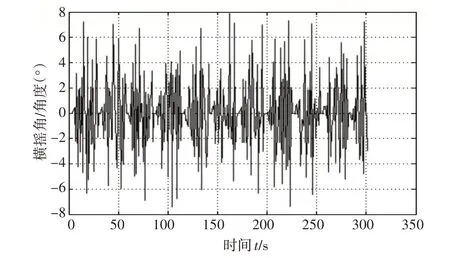
图4 在航速18节，遭遇角为30°，有义波高为3.8m时，横摇角的变化

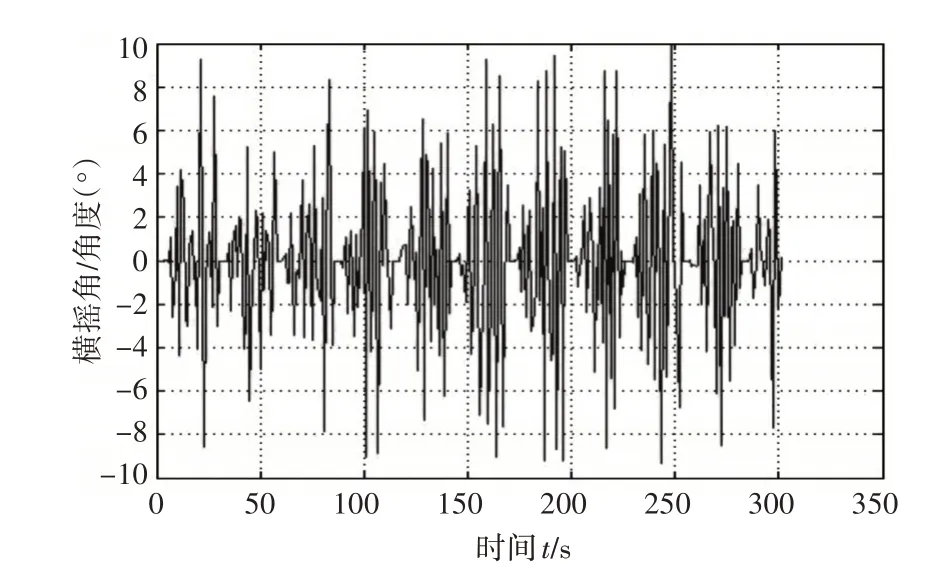
图5 在航速18节，遭遇角为30°，有义波高为7m时，横摇角的变化

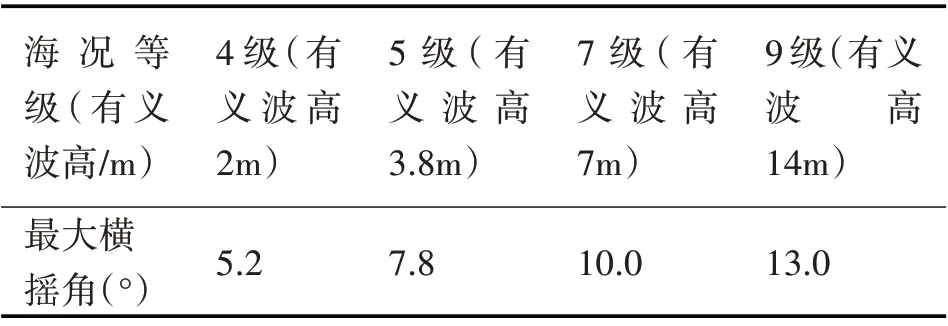
表2 不同海况下船舶最大横摇角

3.2 探究不同遭遇角下海浪对船舶横摇角的影响

本实验中，本文设定船舶的航速和所处海况等级不变，探究不同遭遇角下船舶的横摇角变化。

1）在船舶零航速、有义波高为3.8m，遭遇角为30°时，船舶横摇角变化（如图6）。

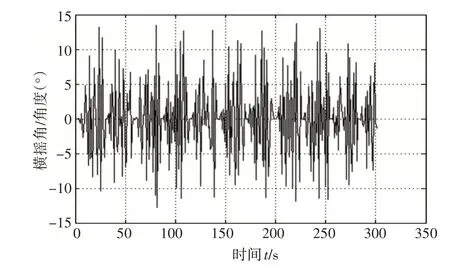
图6 在航速0节，遭遇角为30°，有义波高为3.8m时，横摇角的变化

2）在船舶零航速、有义波高为3.8m，遭遇角为60°时，船舶横摇角变化（如图7）。

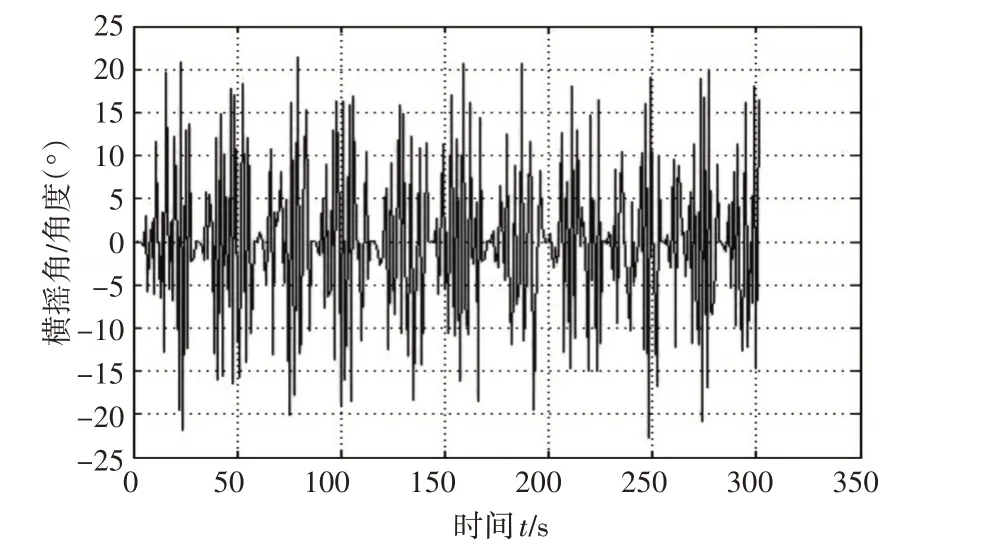
图7 在航速0节，遭遇角为60°，有义波高为3.8m时，横摇角的变化

3）在船舶零航速、有义波高为3.8m，遭遇角为90°时，船舶横摇角变化（如图8）。

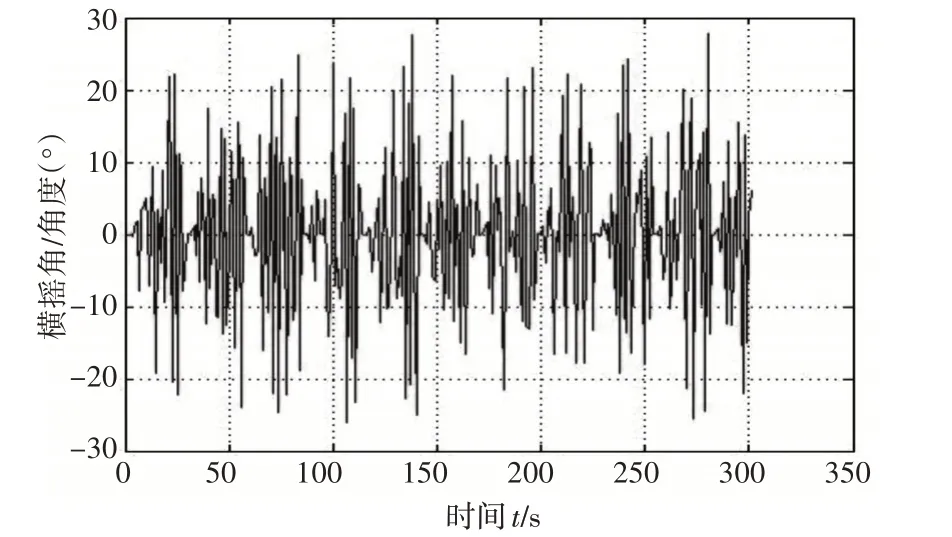
图8 在航速0节，遭遇角为90°，有义波高为3.8m时，横摇角的变化

4）在船舶零航速、有义波高为3.8m，遭遇角为120°时，船舶横摇角变化（如图9）。

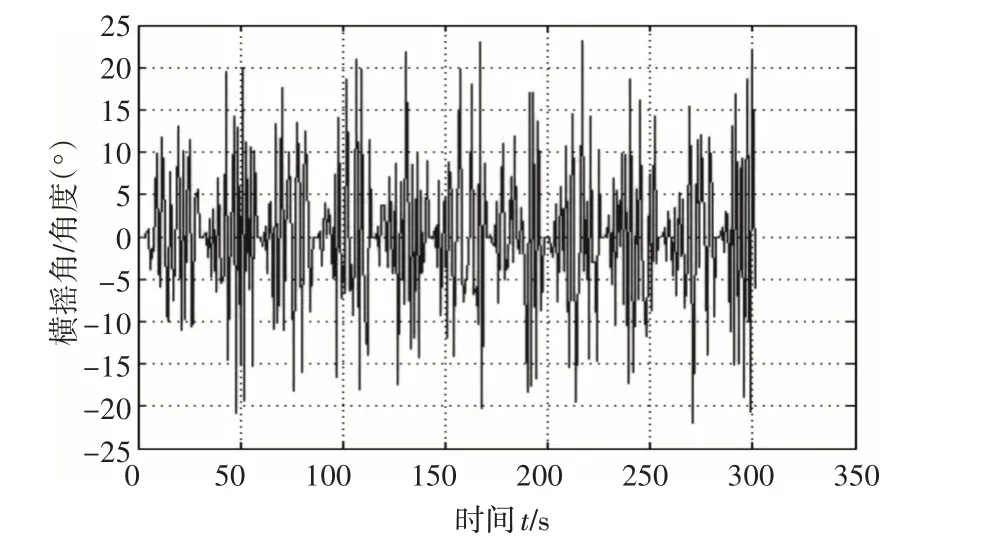
图9 在航速0节，遭遇角为120°，有义波高为3.8m时，横摇角的变化

根据仿真实验可得在航速0 节，海况等级为5级（有义波高为3.8m）时，不同遭遇角下船舶横摇角的变化如下表3。

表3 不同遭遇角下船舶最大横摇角

对比图6、图7、图8、图9结合表3可以看出，在船舶航速和海况等级不变时，船舶受海浪影响产生的横摇角随船舶与海浪的遭遇角变化而变化，在0°～90°范围内，船舶横摇角随遭遇角的增大而增大，在遭遇角为90°时达到最大；在90°～180°范围内，横摇角随着遭遇角增大而减小。并且在船舶零航速时，由于船舶关于横轴对称性，遭遇角为30°和150°，60°和120°下的最大横摇角基本相等。

3.3 探究不同航速对船舶横摇角的影响

在本实验中，本文保持海况等级不变，船舶与海浪的遭遇角不变，探究不同航速下海浪对该船舶在产生的横摇角变化规律。

1）在海浪有义波高3.8m 环境下，假设船舶遭遇角为30°不变，观察零航速下船舶横摇角变化（如图6）。

2）在海浪有义波高3.8m 环境下，假设船舶遭遇角为30°不变，观察航速18 节下船舶横摇角变化（如图4）。

3）在海浪有义波高3.8m 环境下，假设船舶遭遇角为30°不变，观察航速27 节下船舶横摇角变化（如图10）。

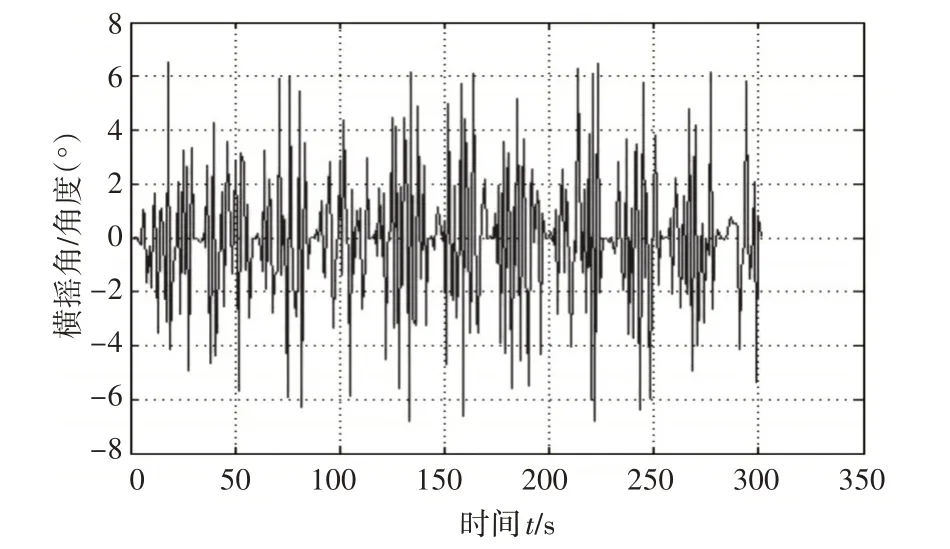
图10 在航速27节，遭遇角为30°，有义波高为3.8m时，横摇角的变化

根据仿真实验可得在海况为5 级（有义波高3.8m），遭遇角30°，不同航速下船舶最大横摇角的变化如表4。

表4 不同航速下船舶最大横摇角

对比图6、图4、图10 结合表4 可以发现，在海况和船舶遭遇角不变的情况下，船舶横摇角和船舶航速相关。随着船舶航速增加，横摇角的幅值有减小趋势。

3.4 探究船舶在恶劣环境下的横摇运动

根据上文得出海浪影响下船舶横摇角在航速、航向以及海况影响因素下的变化规律，分析船舶可能出现的最大的横摇角环境。实验得出遭遇角为90°和270°时，海浪引起船舶横摇角越大；随着船舶航速降低，海浪引起船舶横摇角越大。

根据以上结论，本文在船舶零航速与海浪遭遇角为90°情况下，仿真探究船舶在恶劣海况下的横摇规律，以探究船舶可能受到的最大海浪干扰，分析其安全性。

表5 不同海况下船舶最大横摇角

由表5 可以看出，海浪引起的船舶横摇在9 级海况（有义波高＞14m）时达到最大，由于在现实生活中很少能见到波高20m的海浪，因此本文有义波高最大取20m，这时候该船舶横摇角可以达到49.5°，具有较大倾斜，对船舶影响较大，因此对船舶进行减摇具有重大意义。

4 结语

本文将新型船舶的实际船体参数带入海浪干扰模型和船舶运动模型，通过建立的Matlab仿真平台进行实验。考虑到影响船舶横摇角的因素主要是海况、船舶航向（遭遇角）和航速。本文中，通过控制变量法，依次对以上影响因子进行探究。经过仿真实验得出以下结论:

1）船舶在海中航行，受海浪干扰产生的横摇角随海况等级的变化而变化，在船舶航速和航向（船舶与海浪遭遇角）不变情况下，随着海况等级的升高，船舶的横摇角幅值越大。

2）船舶在海中航行，受海浪干扰产生的横摇角与船舶航向有关，这里航向主要体现在船舶相对海浪的方向即遭遇角。遭遇角的取值范围为[0 ，360°] ，在[0 ，90°] 区间内横摇角随着遭遇角的增大而增大；在[9 0°，180°] 区间内，横摇角随着遭遇角的增大而减小；在[1 80°，270°] 区间内横摇角随着遭遇角的增大而增大；在[ ]270°，360° 区间内，横摇角随着遭遇角的增大而减小；其中在遭遇角为90°和270°时，横摇角达到最大峰值。

3）船舶在海中航行，受海浪干扰产生的横摇角与船舶航速有关，在船舶航向和海况不变情况下，船舶航速越大，船舶横摇角越小。

4）当船舶处于极恶劣海况条件下，船舶的横摇可以达到50°，对船舶的作战性能甚至安全影响很大，运用合理的减摇手段进行减摇很有必要。

本文通过模拟仿真实验，得出该船舶在海中航行时，船舶横摇角随海况、航速和航向的变化规律，对本船受海浪影响的横摇运动有初步认识，为该新型船舶下一步减摇提供了思路。并且根据海浪影响规律设计恶劣情况，仿真该船舶在恶劣情况下的横摇，分析其耐波性和安全性，具有重要的现实意义。