基于NSGA-Ⅱ算法的备件存储分配优化研究∗

柴志君 欧阳中辉 刘文彪

（1.海军航空大学岸防兵学院研究生大队 烟台 264001）（2.海军航空大学岸防兵学院304教研室 烟台 264001）

1 引言

随着我国航母事业的发展，航母战斗力的逐步形成，以及出海、训练等任务的不断增多，所面临的保障问题也越来越多。航母上的备件舱空间十分有限，因此怎样合理有效地利用有限的空间，使备件得到最优化的存储，是一个亟需解决的问题。目前，舰上备件存储分配以人工为主，所依赖的是舰员的知识和经验，其效率会因人而异，虽然减少了计算机等设备投入费用，但存在明显缺点:出错率高、分配效率低、需要大量人力。为解决这一问题，可采用计算机辅助分配方式。这种分配方式是利用图形监控系统，收集备件存放位置信息并显示其使用情况，供舰员实时查询，为备件存储分配提供参考，可以很好地解决人工分配存在的不足［1～3］。

2 备件存储分配的优化

2.1 基本原则

1）备件存放架的受力情况良好。较重的备件存放在较低的位置，较轻的备件存放在高处的位置，以保证存放架相对稳定和牢固。备件应分散在存放舱室的不同位置，以避免由于集中存放而引起存放架受力不均等问题。

2）提高备件使用效率。使用频率越高的备件所存放的位置应更容易取存，并且离存放舱室的出入口更近，以缩短应急情况下取用备件所需的时间。同种备件使用时，应先取用先入舱室存放的备件，以避免因备件长期积压造成锈蚀、变形、变质等损坏［4～6］。

2.2 建立数学模型

设备件的种类编号依次为｛1，2，…，p｝，其中i类备件的立方体索引号COI（cube per order index）值为Ih（0 ＜h ≤p）:

其中:Ch为h 类备件存储所需的容量，fh为h 类备件的出库频率。

COI 值的大小描述了备件出入库频率的高低。给定一个m 层n 排的备件存放架，设每个备件存放位长度为L，高度为H，并把最低层记为第1层，距离巷道口最近的排记为第1 排，处于第i排第j 层的备件存放位置记为（i，j）（i=1，2，…，n；j=1，2，…，m）。

1）为保证备件存放架受力情况良好，应使质量（用mij表示）较小的备件尽量放在存放架的高处，即:

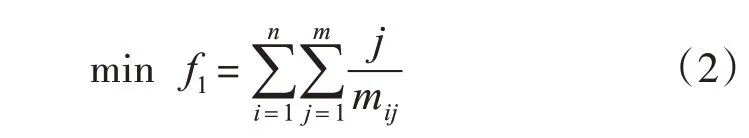
式中:f1为备件所在层编号与质量mij之商。

2）为实现备件使用效率最大化，所有备件的COI 值就应与其所分配的备件区编号的乘积之和尽可能小［7～10］，即:

2.3 约束条件

1）在文献［7］中，POTRC 对货架宽度与高度之比对立体仓库性能产生的影响进行了讨论，这里作为备件存放架性能的参考，根据文中的计算结果，设宽度为L，高度为H，则理想比值为

2）备件在任意两点（i1，j1）和（i2，j2）进行存放作业时，存放次序应该满足由近及远的原则，即:i1≤i2，j1≤j2。 而备件在任意两点（i3，j3）和（i4，j4）进行取出操作时，则应满足由远及近的原则，即:

3）在存放备件时，要保证备件所存储的位置为空，即:

对备件存储分配的优化，需要同时满足式（2）～（3）的要求。这两个公式一般情况下是相互矛盾的，所以优化问题的求解就是一个多目标优化问题。加入约束条件（4）～（6）后，该问题就成为一个约束多目标优化问题。对于约束多目标优化问题的求解，一般可以采用如下数学模型进行描述［11］:

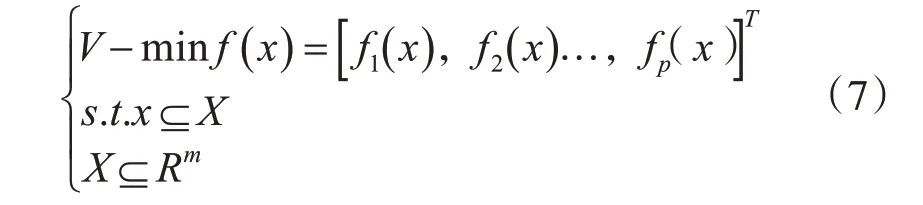
3 NSGA-II多目标优化算法介绍

多目标优化问题（MPO）［12］在现实生活和工程应用中都具有非常重要的地位，这些问题通常具有复杂的约束条件，各约束条件和目标函数之间又存在复杂多样的联系。NSGA-II 算法（第2 代非劣解排序遗传算法）适应于复杂的多目标优化问题，由K-Deb 教授于2002 在论文《A Fast and Elitist Multiobjective Genetic Algorithm:NSGA-II》中提出，是目前最优秀的进化多目标算法之一［13］。

NSGA-Ⅱ算法的运算步骤主要有种群初始化（initialize variables）、快速非支配排序和拥挤都计算（non dominate sort and crowding distance）、锦标赛选择（tournament selection）、遗传操作（genetic operator 包括交叉和变异操作）、替代操作（replace chromosome）。

NSGA-II 是NSGA 算法的改进版，其改进主要是针对以下三个方面:

1）提出了快速非支配排序算法，一方面使计算复杂度降低，另一方面将父代和子代种群进行合并，使得下一代的种群可以从双倍的空间中进行选取，进而使保留的所有个体最优化；

2）引进精英策略，以确保在进化过程中某些优良的种群个体不会被丢弃，从而提高了优化结果的准确度；

3）采用拥挤度和拥挤度比较算子，不但克服了NSGA 中需要人为指定共享参数的缺陷，而且将其作为种群中个体间的比较标准，使得准Pareto 域中的个体能均匀地扩展到整个Pareto 域，保证了种群的多样性［14～16］。

4 备件存储分配优化模型计算及仿真

鉴于NSGA-II 的以上优点和在处理多目标约束优化问题上的成功应用，本文基于NSGA-Ⅱ算法对模型进行求解，并将结果与多目标粒子群算法（MPSO）对比说明。考察某备件舱A 存放架为6排、10层，架宽为20cm，备件编号、数量、质量、使用频率等信息情况如表1所示。

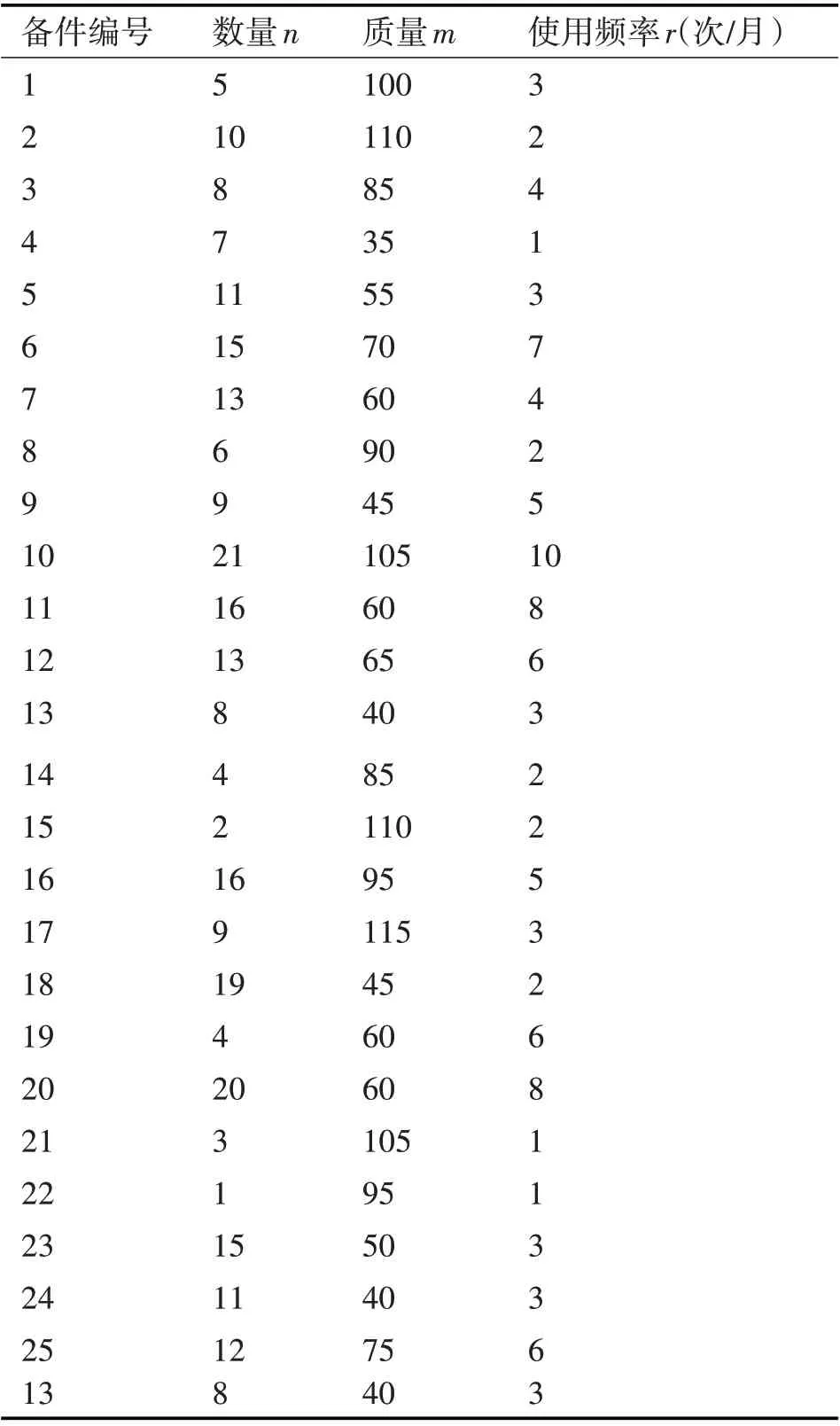
表1 备件信息统计表

本文针对该备件舱存储分配优化模型应用NSGA-Ⅱ算法求解的总流程图如图1所示。

该求解过程的主要步骤有以下几点［17］:

1）随机产生种群大小为200的初始种群P0；

2）计算种群Pt目标函数值并进行非劣排序；

3）对种群Pt执行遗传操作（模拟二进制交叉和多项式变异）得到子代种群Qt；

4）种群合并Rt=Pt∪Ut对Rt中的个体进行非劣排序、拥挤度距离计算；

5）运用锦标赛规则选择并保留精英个体选取前N 个个体作为父代种群Pt+1；

6）循环执行程序并进行终止条件判断，按照事先设置好最大遗传代数判断，若t＞400算法终止。

在试验中，取种群最大规模为200，交叉概率pc=0.7，变异概率pm=0.1，最大允许进化代数Genmax=400，采用Matlab 平台构造备件存储分配优化模型并进行仿真［18～21］，可得目标函数f1和f2的迭代曲线如图2和图3所示。

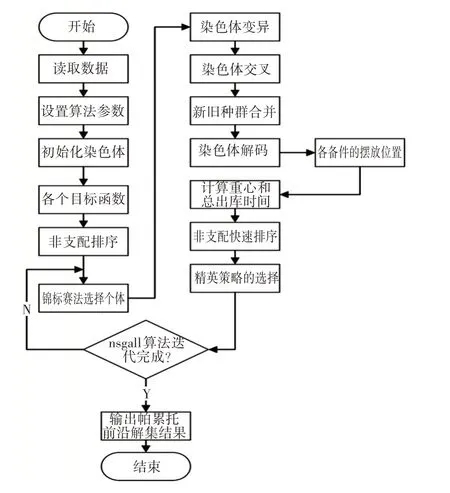
图1 模型求解总流程图

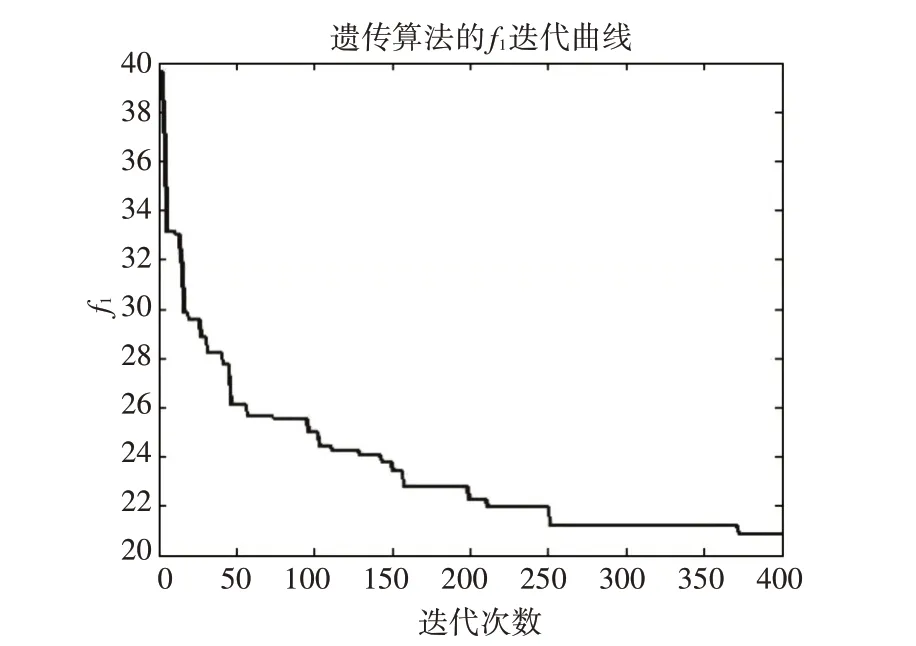
图2 目标函数f1 的迭代曲线

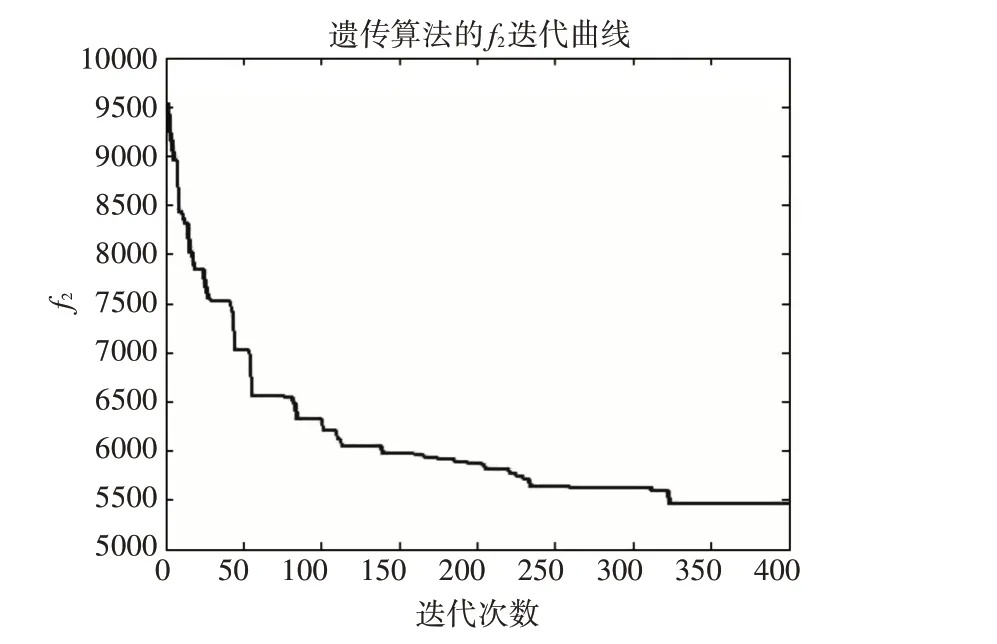
图3 目标函数f2 的迭代曲线

5 结果分析

本文在对备件舱A 备件存储分配优化过程中，求解模型时采用了NSGA-Ⅱ算法和MPSO 算法来进行效果比较，得到两种算法的帕累托（Pareto）前沿如图4所示。

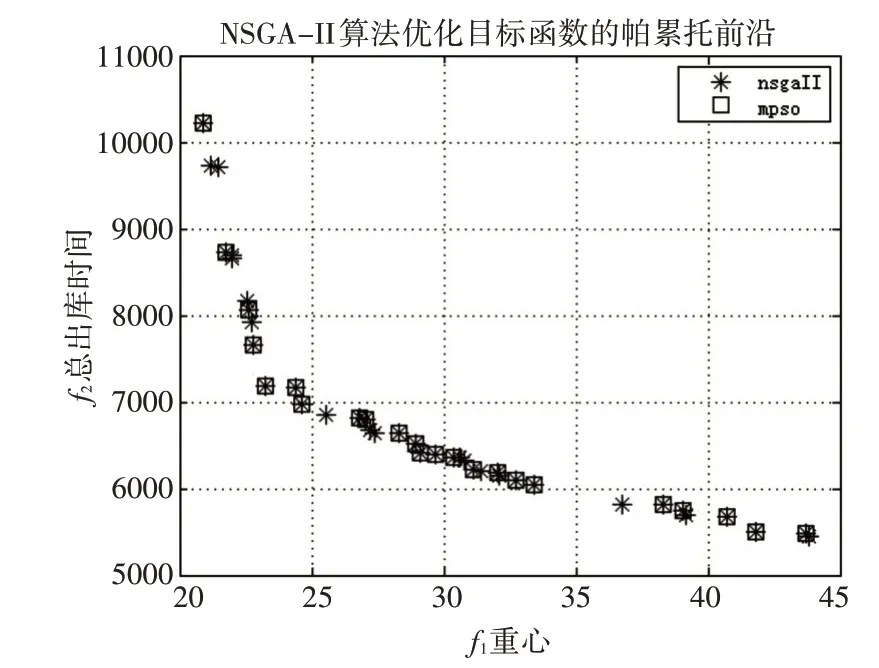
图4 帕累托前沿比较图

从图4 可以看出NSGA-Ⅱ算法的帕累托前沿点数多于MPSO 算法的点数，说明NSGA-Ⅱ算法的求解效果要优于MPSO 求解结果，证明该算法在求解备件存储分配优化问题上具有优越性。

通过NSGA-Ⅱ算法求解对表1 中备件原存储方法（如图5所示）进行优化，可得到图6所示结果。

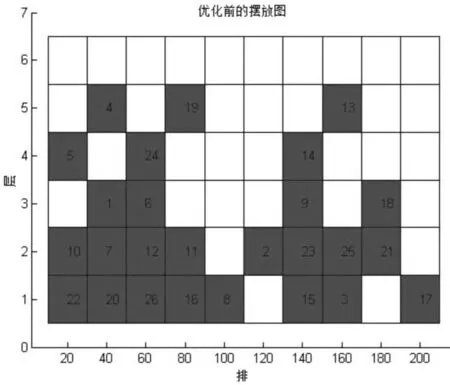
图5 优化前的摆放图

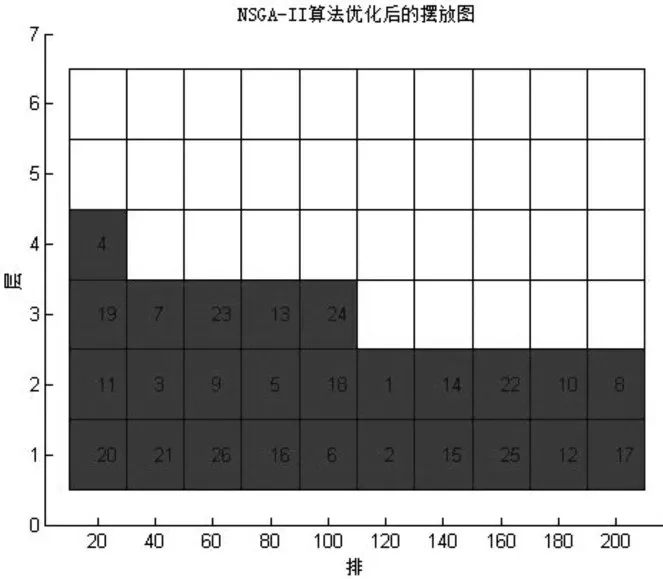
图6 优化后的摆放图

图中（0，0）点表示备件舱出口，可以看出经过优化后的备件存放位置满足f1和f2目标函数最小化的要求，证明了NSGA-Ⅱ算法在求解备件存储分配优化问题上具有可行性。

6 结语

本文以最低出库时间和最低重心为目标函数，考虑了基本约束、存放架高度和宽度对性能影响以及存取原则等方面的约束建立存储分配模型。对某备件舱A 进行优化模型的计算与仿真，运用NSGA-Ⅱ算法计算过程中可得到足够多且分布均匀地Pareto 前沿，并与MPSO 算法计算结果进行比较，证明其优越性。NSGA-Ⅱ算法作为进化算法中最成熟、应用最广泛的算法之一，其收敛速度快，约束表示灵活，算法的准确性高稳定性好。最后通过仿真得出优化后的备件摆放图，进一步证明NSGA-Ⅱ算法在解决备件存储分配优化问题中的可行性，为在舰上采用计算机辅助分配方法管理备件提供了参考。