基于语音活动性检测的维纳滤波处理∗

于春和 朱雨薇

（沈阳航空航天大学电子信息工程学院 沈阳 110136）

1 引言

人们可以通过语音来表达情感和信息，语音也成为一种重要的交流方式。随着科技的不断更新和发展，通信领域被人们越来越重视。例如手机智能语音助手，手机通话等方面。但是在语音传输的过程中，总是会产生噪音，这些噪音主要是由于受到背景环境和传输环境的影响而产生的。同样，语音信号的产生过程和处理过程也会产生噪声。噪声可以是白高斯噪声、宽带和窄带噪声、加性噪声、电学或者声学噪声，也可以是与原始纯净语音无关的其它语音信号。在这些条件的干扰下，语音的可懂度和语音质量会大幅度下降，产生可逆或不可逆的影响。但是噪音的产生具有随机性，我们只能是尽量减小，并不能做到完全的消除。一般我们用语音的语音质量和可懂度这两个指标来评价处理语音信号的好坏。这两个评价指标有联系而又不同。语音质量是通过信噪比的值来反映出来，目标是提高信噪比。而语音的可懂度则需要人们主观去判断。具有高可懂度的语音信号在各个领域都起着重要的作用。既然噪声的产生无法避免，我们就要想办法来处理它们。

2 语音的预处理

在处理语音信号的问题上我们先要讨论信号的预加重、分帧和加窗问题，才能进一步对信号进行具体的处理。

2.1 预加重

语音信号受生理因素的干扰，会对语音产生一些影响，高频部分通常按着一定倍频程衰减，在衰减过程中频谱的频率越高，其频谱幅值越小，反过来，频率越低，频谱幅值越大。我们如果要消除这种影响，取消其不均匀的分布，需要对语音信号进行预加重处理。加重语音的高频部分，去除口唇辐射对语音信号造成的影响，同时也需要增加语音的高频分辨率。一般通过传递函数为

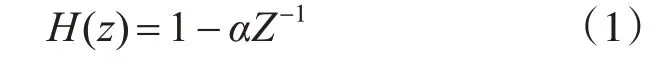
的高通数字滤波器来实现预加重，预加重系数设置为α，其取值范围设置为0.9～1。在n 时刻时，语音采样值可以表达为x（n），经过预加重处理后的结果为

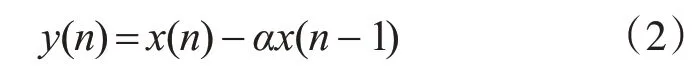
2.2 语音信号分帧、加窗处理

根据语音时长可以看出，语音信号有长有短，有的短则几秒钟，有的长达几分钟，甚至更长。在宏观上来看，长的语音信号不满足平稳特性，我们可以认为其是不平稳信号。但是在维纳滤波等一些处理方法中，要求信号必须是在平稳信号下进行处理的。根据语音信号具有短时平稳特性，我们可以对语音信号进行分段处理，每一个短段称为一帧。这些段落长度相同，都带有语音的详细特性。我们称这个过程为语音信号的分帧处理。一帧语音的长度可以根据需要来设定，但是要保证在10ms～30ms之间。

加窗操作即语音信号与一个窗函数相乘，其是为了使整个语音信号更加连续，避免出现一种效应，即吉布斯效应。加窗函数的时候，我们也使本来没有周期性的语音信号获得了周期函数的部分特征。

但是加窗会造成一定后果，其使每一帧信号的两端部分会造成削弱，为了后续加窗的操作，我们一般在分帧的时候，需要相互重叠一部分。而不是不要背靠背地截取，相邻两帧的起始位置上存在的时差叫做帧移。

在语音信号处理中常用的窗函数有矩形窗、汉宁窗等。

2.2.1 矩形窗

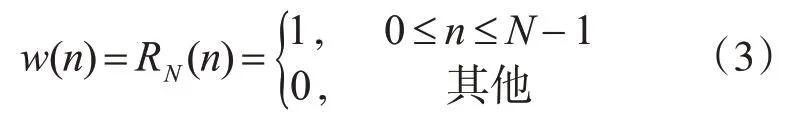
其中帧长为N。将其进行傅里叶变换求得矩形窗的频谱:

幅度谱为R（W），如图1所示。

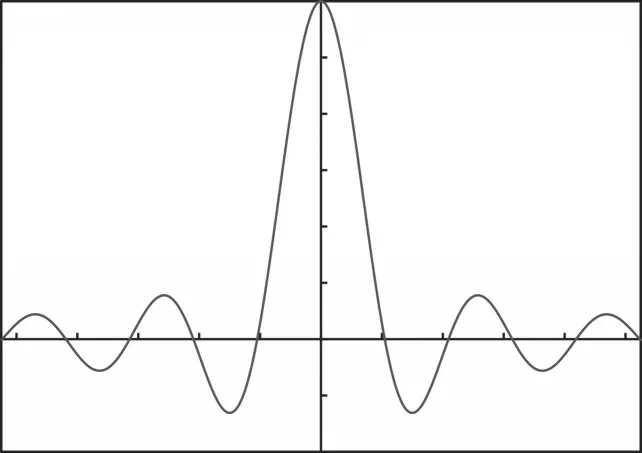
图1 矩形窗的幅度谱

这是一个逐渐削弱的衰减函数，x 轴的正半轴第一个过零的在点w1=2π/N处，x轴的负半轴的在w2=-2π/N处第一个过零点，ω1和ω2之间的距离叫做主瓣，矩形窗的主瓣宽为4π/N，其两边的旁瓣各占二分之一，均为2π/N。

2.2.2 巴特利窗

从其表达式可以看出巴特利窗是一种三角窗，两端为0，中间为最大值。

其频谱为

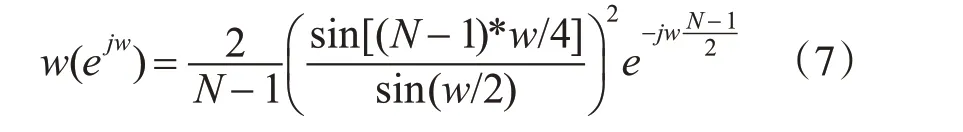
其幅度谱为R（w），如图2所示。

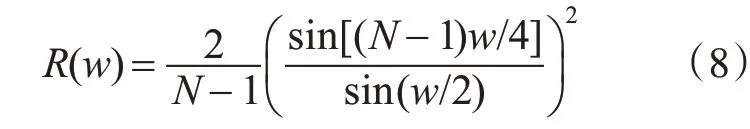
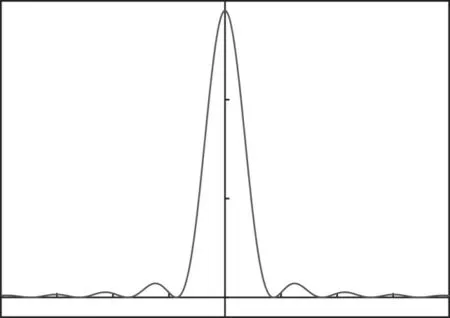
图2 巴特利窗的幅度谱

和矩形窗的频谱相比，巴特利窗的频谱最大旁瓣的幅度降低了很多。但时其主瓣宽度和过渡带宽增加了。

2.2.3 汉宁窗

其也是一种常用的窗函数，其中RN(n)是长度为N 的矩形窗。其频谱为

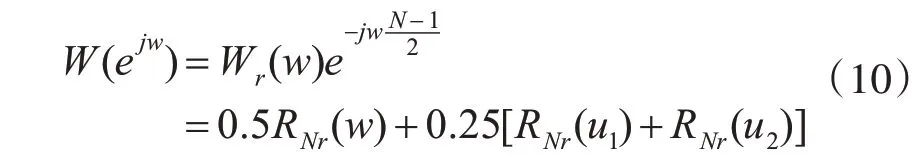
矩形窗的幅度谱表示为RNr，如图3所示。

3 个分量之和构成了其幅度谱，导致其旁瓣相互抵消，旁瓣减小。与矩形窗的幅度谱相比，我们很容易看出其能量更加集中到主瓣，主瓣加宽。

图3 汉宁窗的幅度谱

2.2.4 汉明窗

改变汉宁窗定义式中的系数0.5则可以得到汉明窗。即汉明窗是汉宁窗的升级版。

图4 为汉明窗的幅度谱，与图3 相比，汉明窗幅度谱旁瓣更小，从而使得能量更加集中到主瓣。

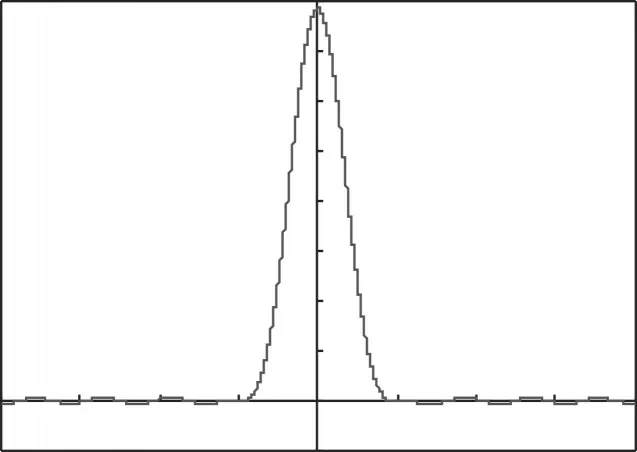
图4 汉明窗的幅度谱

加窗分帧可以采用前后两帧完全不重叠的连续分帧；也可以前后两帧完全有部分重叠的叠分帧。但是一般都采用重叠分帧的方法。这是为了保证前后两帧参数能够平稳的过渡。帧移则表示为前一帧和后一帧的重复部分。帧移与帧长的比值在0～0.5范围内选取。当帧移取0时表示连续分帧，即相当于前后两帧没有交叠重复部分，当帧移取0.5时表示前后两帧有一半重叠的分帧。

3 维纳滤波器

滤波器就是一个含有噪声的信号，经过这个滤波器之后，输入信号变成了另一个信号。只不过这个信号比较特殊，它和原来的信号有联系，这个联系就是原来的信号是现在的信号的+噪声信号。维纳滤波器是一种以语音信号衰减为代价而实现噪声抑制［1］的滤波器。也是常用的线性滤波器之一。它是对语音处理的关键的一个部分。

假设所有信号都是平稳的，纯净语音信号y（n）受到噪声信号v（n）干扰，带噪信号可以表示为

其中带噪信号v（n）是与纯净语音信号y（n）不相关的白噪声或者有色噪声［2］。

当带噪信号s（n）输入到维纳滤波器后，可以得到输出信号ss（n），使得输出信号ss（n）尽可能接近纯净信号y（n），即均方差E{e(n)2} 最小，可以表示为

其中h（n）为单位冲击响应。均方误差MSE 准则［3］可以表示为

其中:

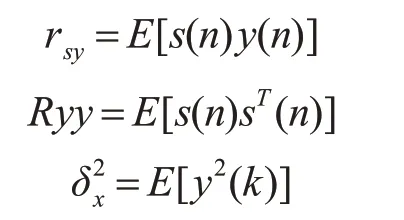
其中Ryy表示带噪信号s（n）自相关矩阵，rsy表示带噪信号和纯净信号的互相关矢量，δ2为信号y（n）的方差，E[.]表示数学期望。可以得到最优维纳录波器为［4］

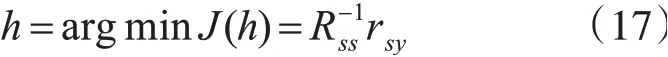
然而在现实当中我们往往不知道纯净信号y（n）的信息，这就使得rsy［5］很难获得。但是通过以下公式的推导:

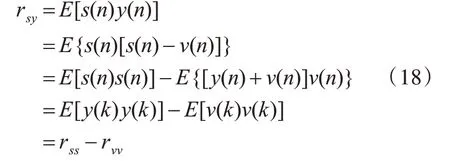
我们可以找到噪语音信号与噪声信号互相关函数和带噪语音自相关函数与噪声信号自相关函数之间的联系。

从中可以看出带噪信号和纯净信号的互相关矢量取决于带噪信号的自相关矢量和噪声信号的自相关矢量。其中带噪信号的自相关矢量可以通过纯净信号和噪声信号混合时得到，噪声信号的自相关矢量，可以在只有噪声存在的时刻估计得到。为了解决这一问题，需要提前对噪声进行估计，这一步就显得十分重要，这里利用语音活动性检测的方法从带噪语音中提取纯净的噪声片段，从而估计其自相关矩阵。

4 语音活动性检测

语音活性检测［6］是一项用于语音处理的技术，简称VAD。其目的是检测语音信号的存在与否。VAD 技术通常在语音编码和语音识别［7］方面应用。它可以简化语音处理，也可用于在视频通话的时候出去非语音信号，可以在IP 电话应用中避免对静音数据包的编码和传输，从而节省了计算时间和带宽［8］。

VAD 有很多种方法。在实际处理中，为了提高其精确度往往会提取四种或者更多的特征进行判断［9］，此处介绍的是利用短时能量（简称STE）和过零率（简称ZCC）的检测方法［9］。

4.1 过零率

过零率是指一个信号的符号变化的比率，即一帧语音时域信号穿过时间轴的次数。

其计算方法是，将帧内所有信号平移1，再对应点做乘积，符号为负的则说明此处过零，只需将帧内所有负数乘积数值求出则得到该帧的过零率。

4.2 短时能量

短时能量是指一帧语音信号的能量［10］。由于随着时间变化信号能量也随之变化，清音和浊音之间的能量差别相当显著。利用短时能量可以很好地进行处理。

可以定义为［11］

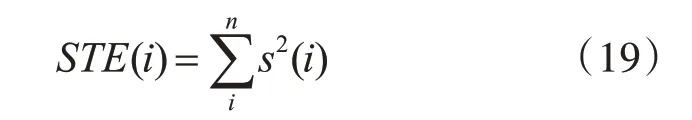
在信噪比不是很低的前提下，语音片段的STE相对较大，ZCC 相对较小；而非语音片段的STE 相对较小，ZCC相对较大［12］。主要是由于语音信号能量绝大部分包含在低频带内，而噪音信号通常能量较小且含有较高频段的信息而造成的。所以可以设置两个门限通过语音信号这两个特征进行对比，从得得到想要的非语音信号，进行下一步维纳滤波的操作。

5 实验分析和结果

Matlab［13］是一款在算法开发时经常用到的数学软件。因此在维纳滤波处理和运用上，我们也将使用这个便捷的计算软件。主要考虑的是输入的带噪信号s（x）的自相关函数Rs（x）和带噪信号s（x）和纯净信号y（x）的互相关函数Rsy（x）。

本文实验取一段在安静环境下录制的30s 语音作为纯净始语音y（n），并加入不同信噪比的高斯白噪，得到带噪信号s（n）。

在维纳滤波阶段，根据带噪信号s（n）和VAD估计得噪声信号v（n），通过Matlab 可以求解维纳-霍夫方程得出系统函数［14］:

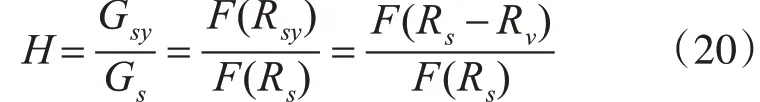
其中R 为相关函数，其傅立叶变换为G。进一步计算输出信号ss（n）与输入信号y（n）的均方误差值，可以得到最优维纳滤波输出信号。

在根据语音活动性检测来估计噪声v（n）的阶段，首先需要对语音信号进行预处理［15］，本实验取采样频率为fs，一帧长度为0.02fs。对语音信号进行分段处理，计算短时能量和过零率，通过STE 和ZCC这两个特征并且与两个门限进行对比，从而判断非语音信号［16］。

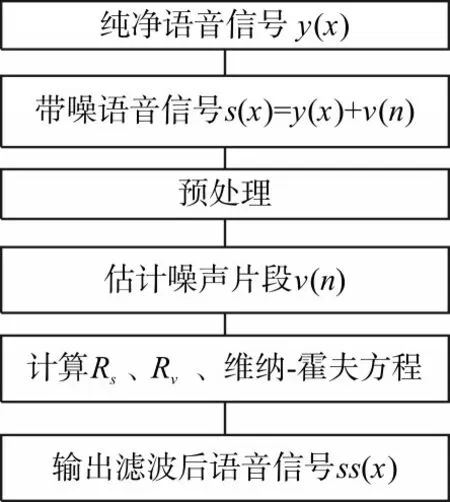
图5 流程图

5.1 加噪处理

我们录制了30s 的语音信号作为试验的数据，对录制的语音信号，加入已知信噪比为60 的白噪声，用来评定噪声信号估计的结果是否与加入的白噪声接近。录制信号加入白噪声后频谱如图6所示。

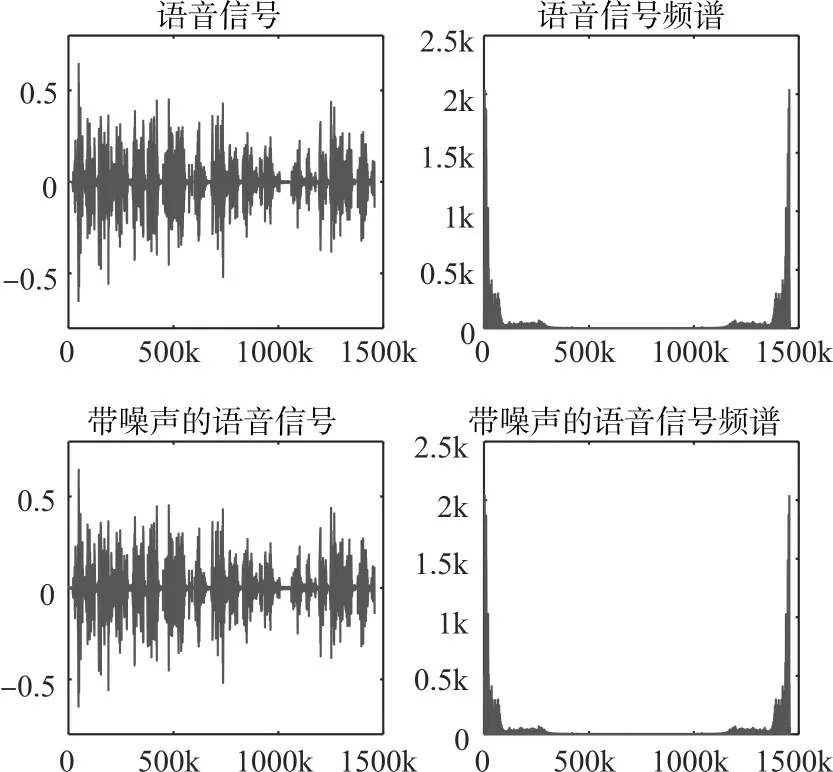
图6 语音信号加噪声

5.2 预处理

为了加重语音的高频部分，消除口唇辐射对语音信号的干扰，需要对带噪语音进行操作，这个过程就叫做预加重。从图7 可以看出预加重后得到的语音更符合我们的要求。

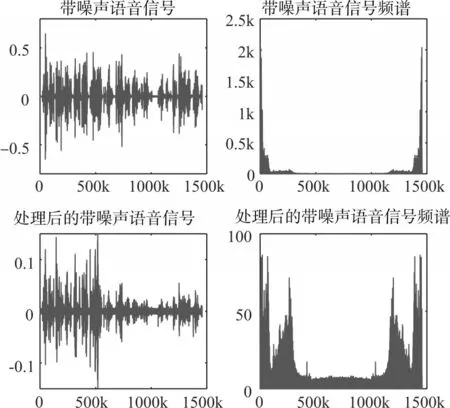
图7 预加重处理

为了得到平稳信号，我们对语音信号进行了分针加窗处理，在已知录制语音的采样频率为fs的前提下，取一帧的长度L 为0.02ms，帧移为0.5L。窗函数选取为汉明窗。可以得到语音信号，如图8 所示为加窗后的一帧信号。

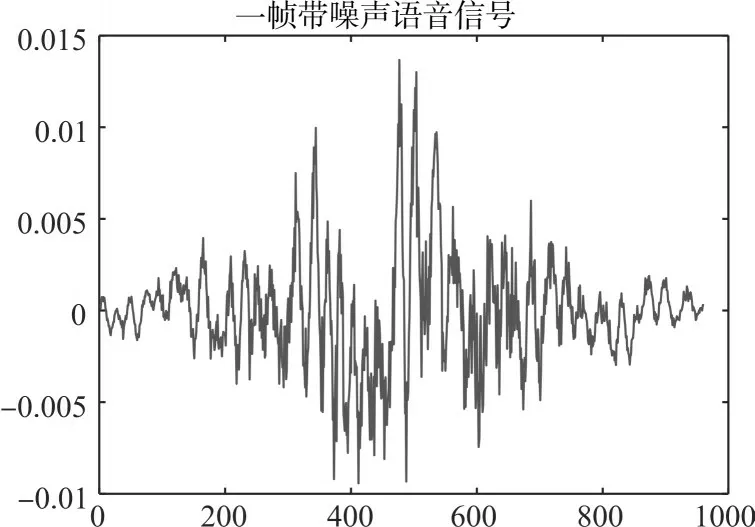
图8 一帧语音信号

5.3 噪声估计

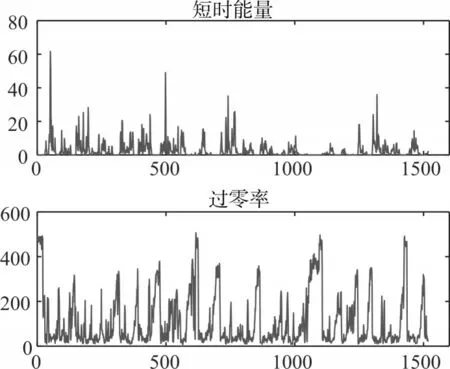
图9 短时能量和过零率

利用过零率和短时能量来做为评判语音活性检测的两个指标，在信噪比为60时。可以从图9观测这两个指标的变化。

生成的检测VAD 和带噪语音进行对比，提取噪声片段。如图10和图11。

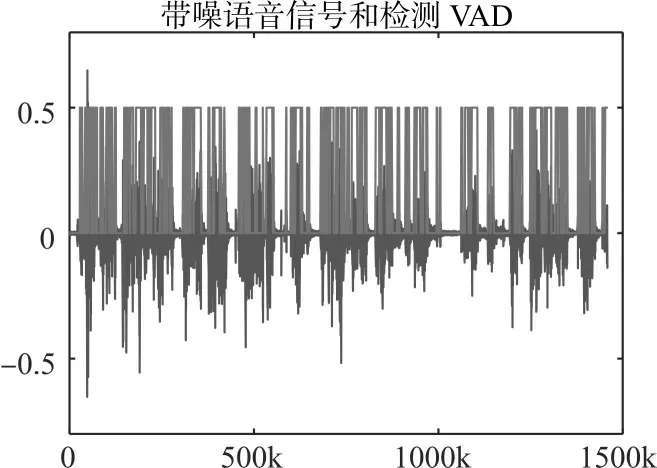
图10 语音活性检测

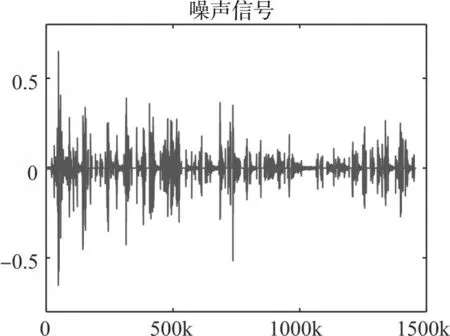
图11 噪声片段

5.4 维纳滤波处理

根据估计的噪声，可以求得噪声信号的自相关矢量。带噪信号的自相关矢量已知，根据公式:

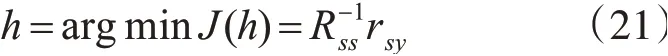
我们很容易求得系统函数。带噪语音信号通过系统后得到的滤波信号为图12。可以看出恢复的信号波形接近原始带噪语音信号。

图12 恢复信号

通过对滤波处理的恢复信号可懂度和信噪比两方面进行分析。语音可懂度大大提高，除去白噪声的语音信号更加清晰。在信噪比方面，本身加入的是信噪比为60 的白噪声。滤波之后信噪比变为80.45。

从这两个指标可以看出，基于语音活动性检测的维纳滤波处理的效果十分明显。我们可以通过这种方法来达到对白噪声的去除。

5.5 信噪比对维纳滤波效果的影响

除此之外，本实验对加入不同信噪比白噪声的语音信号分别进行处理。维纳滤波的目标是使得输出信号无限接近未加噪之前的语音信号，即输出信号和纯净的语音信号最小均方误差最小。当信噪比分别取50～100 时，观察输出信号与纯净信号之间的最小均方误差，形成对比图像。如图13 所示。

图13 不同均方误差结果

从图中可以看出随着信噪比的提高，维纳滤波处理的效果也越来越明显，输出信号无限接近输入信号，我们也更可以得到想要的去噪信号。信噪比的值在50-60 之间时，维纳滤波处理效果大幅上升，而在信噪比大于65 之后，维纳滤波处理效果基于稳定。其不会随着信噪比的提高而提升处理效果。

6 结语

本文先通过语音活性检测对带噪语音进行噪声估计，估计其噪声片段，从而求得维纳滤波系统函数。再通过维纳滤波对带噪语音的处理实现，判断维纳滤波器的线性滤波效特性，获得去噪信号。其次，加入不同信噪比的白噪声，得到系统输出和输入的最小均方误差判断维纳滤波的稳定性和处理效果，滤波输出的期望信号ss（n）越接近纯净信号y（n）。在信噪比达到一定数值时，维纳滤波处理趋于稳定。

维纳滤波的研究有着重要的理论价值和应用价值。它是最佳滤波器研究的基础。它也是语音增强的重要组成部分。此外，维纳滤波也在其他许多声学领域的应用前景也非常广阔。通过仿真实践研究，可以更好地学习这一领域，对今后在通信领域中研究信号处理有很大的帮助，为日后的研究提供了一定的理论依据。我们也要继续在这一领域逐渐成长。