实二阶方阵正整数方幂迹的计算

麦麦提明·阿不都克力木

实二阶方阵正整数方幂迹的计算

麦麦提明·阿不都克力木

（喀什大学 数学与统计学院，新疆 喀什 844006）

迹；行列式；矩阵乘法

1　引言及预备知识

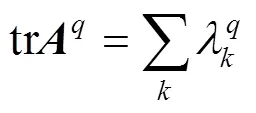
2　主要结果及证明

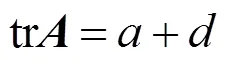
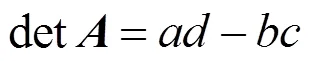
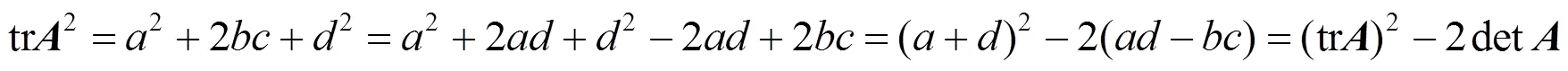
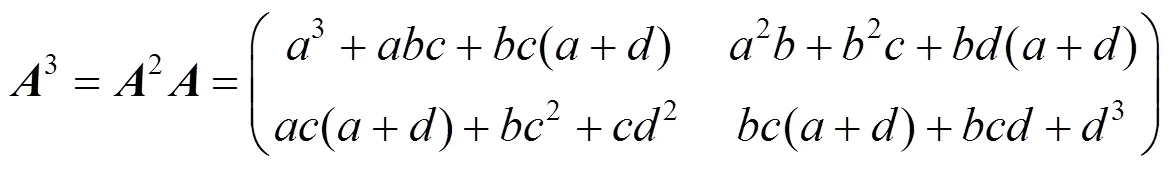
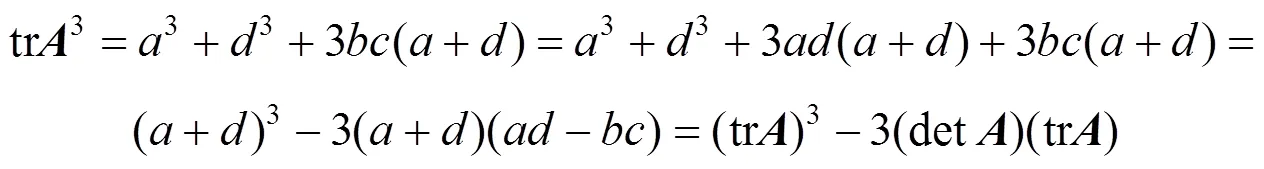
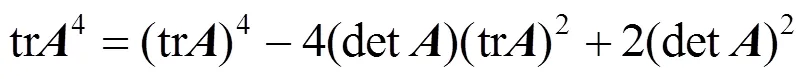
因此

从式（5），（8），（9），（10）中可以观察到

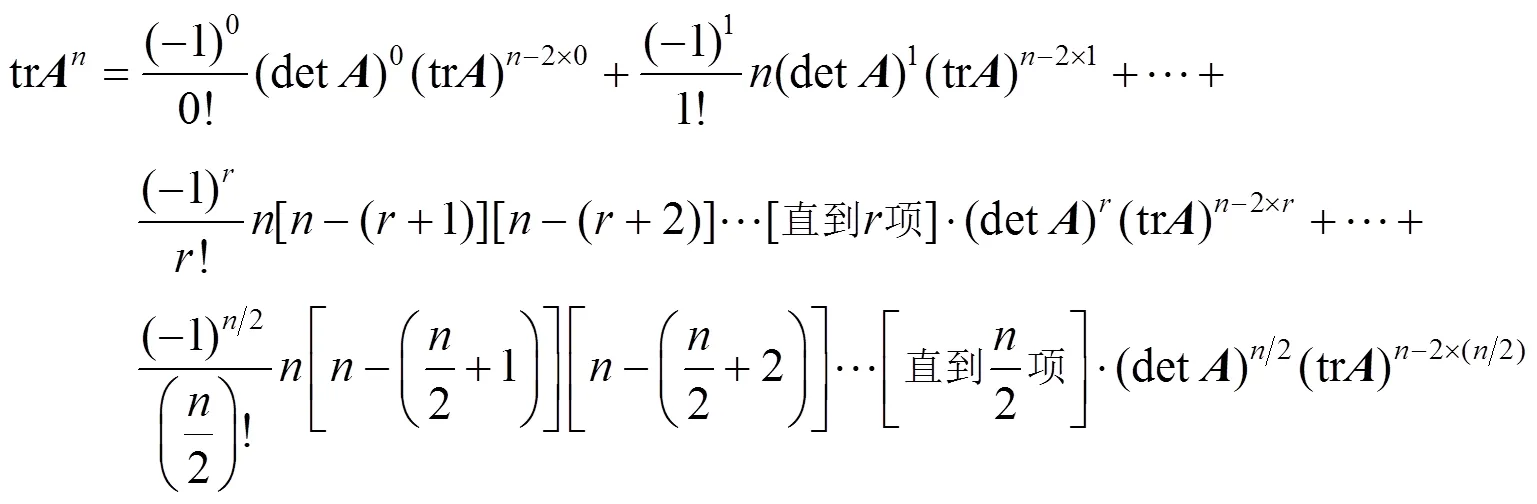
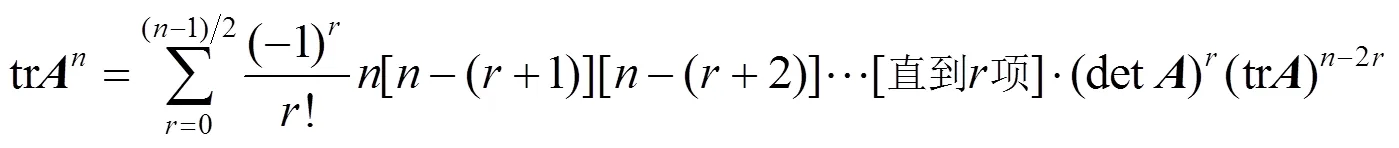
故由式（5）和式（7）可知

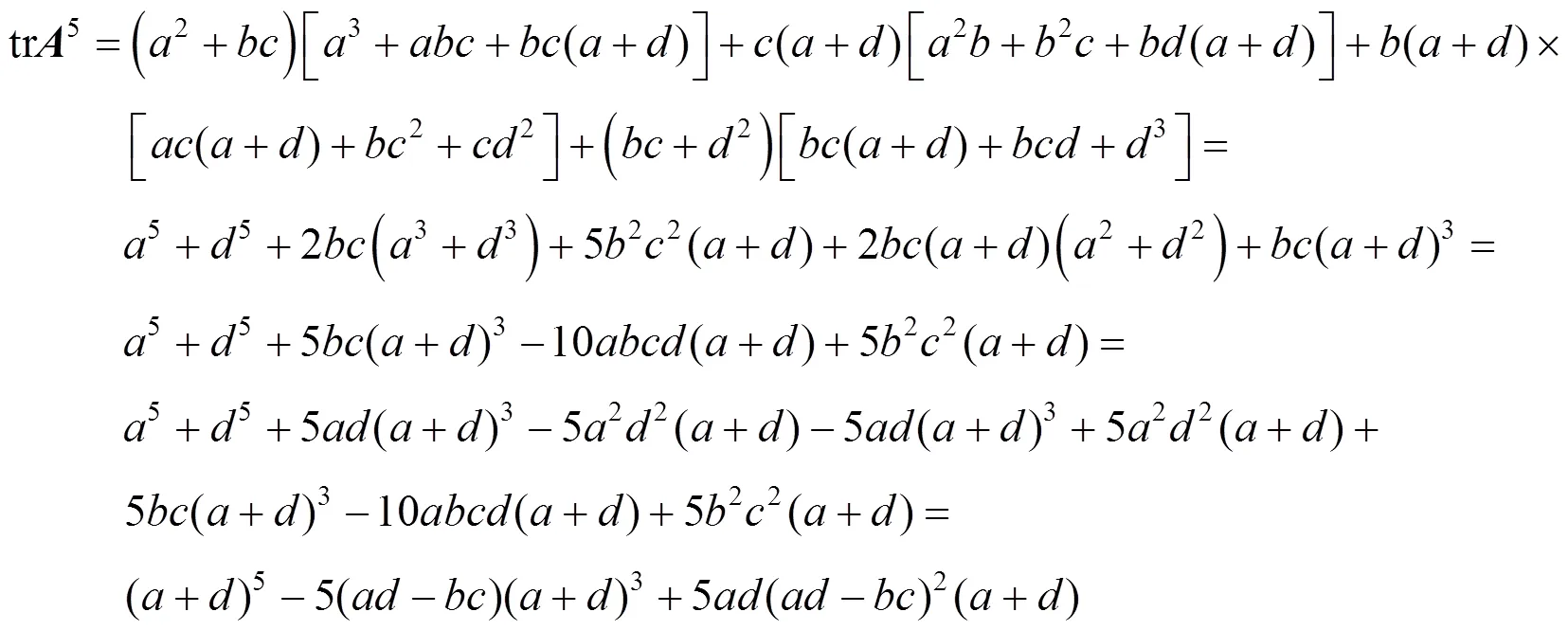
从式（7）和式（13）可以观察到

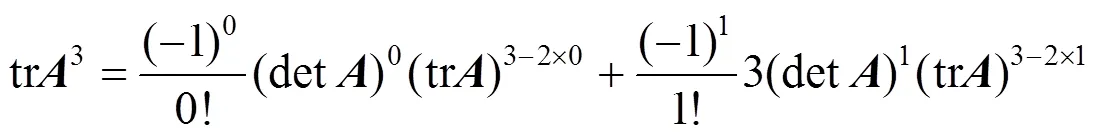
证明直接利用定理1和定理2即可得证． 证毕．

证明由推论2即可得证． 证毕．

3　结语

利用定理1~2和推论1~3，可以求出2×2阶实矩阵正整数幂的迹．用此方法同样可以得到计算3×3阶实矩阵正整数幂的迹的类似结果．

[1] Brezinski C，FikaP．Estimations of the trace of powers of positive self-adjoint operators by extrapolation of the moments[J]．Electronic Transactions on Numerical Analysis，2012（39）：144-155

[2] 徐俊明．图论及其应用[M]．合肥：中国科学技术大学出版社，2010

[3] 方辉，方炜．初等数论中的模法及其应用[J]．黄山学院学报，2009，11（3）：23-27

[4] 张卓．用特征多项式系数计算矩阵方幂的迹[J]．重庆工商大学学报：自然科学版，2014，31（3）：27-30

[5] 吕同富，康兆敏．数值计算方法[M]．2版．北京：清华大学出版社，2013

[6] 殷庆祥．一类三对角矩阵任意正整数幂的计算[J]．大学数学，2010，26（6）：34-39

[7] 张贤达．矩阵分析与应用[M]．2版．北京：清华大学出版社，2013

[8] 陈艳凌．方阵高次幂的算法[J]．长春师范学院学报：自然科学版，2008，27（2）：13-16

Trace calculation of positive integer power of real 2×2 matrices

Mamantimin·Adbikirim

（School of Mathematics and Statistics，Kashi University，Kashi 844006，China）

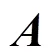
trace；determinant；matrix multiplication

O151.21

A

10.3969/j.issn.1007-9831.2020.03.003

1007-9831（2020）03-0019-04

2019-07-28

麦麦提明·阿不都克力木（1965-），男，新疆喀什人，副教授，从事应用数学研究．E-mail：tougaozhuanxiang01@163.com