非线性不确定离散时变时滞系统的积分滑模控制

张妙清，金朝永，吴丽珍

非线性不确定离散时变时滞系统的积分滑模控制

张妙清，金朝永，吴丽珍

（广东工业大学 应用数学学院，广东 广州 510520）

研究一类非线性不确定离散时变时滞系统的滑模控制问题，构造状态观测器估计所研究系统的状态，在估计状态基础上设计积分滑模面，使整个动态过程对于外部干扰具有完全鲁棒性．利用Lyapunov稳定性理论和线性矩阵不等式（LMI）技术给出了滑模动态系统渐进稳定的充分条件．设计相应的滑模控制器，并在控制器中引入饱和函数消除系统的抖振，利用仿真实例验证所提出方法的有效性．

时变时滞；不确定性；离散时间；滑模控制

随着计算机技术的飞速发展，在实际控制系统越来越多地利用到计算机控制．计算机控制是基于离散釆样系统，由于在实际控制系统中受制于采样过程的限制，不能简单地把连续情形下的算法推广到离散系统中[1]．因此，离散系统研究的重要性变得越来越突出，已经是控制理论研究领域的一个重要组成部分．

滑模变结构控制是变结构控制系统的一种控制策略，在处理参数不确定和外部干扰时显示出很强的鲁棒性[2]．因此，离散系统的滑模变结构控制也成为控制领域研究热点之一．现有文献的滑模变结构研究中大部分采用线性滑模面，虽然它具有参数设计及滑动模态稳定性分析简单容易的优点，但是，同时它也具有系统并不全局鲁棒的缺点．针对这一问题，Utkin[3]提出了积分型滑模控制，受到了很多学者的关注[4-5]．积分滑模可以通过求取合适的初始位置使系统轨迹总是由滑模面开始，保证鲁棒性，避免了线性滑模趋近模态时系统不全局鲁棒的缺点．关于时滞型、变时滞型和不确定时滞型等系统的滑模变结构问题很多学者也做了大量研究，并且取得丰硕的研究成果[6-8]．文献[9]针对状态时滞线性不确定系统，通过非奇异线性变换将系统改写为无时滞的系统，设计积分滑模面．针对非匹配不确定性时滞系统的滑模变结构问题，文献[10]基于线性矩阵不等式（LMI）理论提出了一种自校正滑模控制策略．一般的滑模控制系统全部系统状态可测，所以基于状态反馈的滑模控制研究是最为普遍的[11-13]．然而现实模型中，系统某些状态是不可测的，文献[14]研究了一类具有非匹配不确定的离散系统输出反馈滑模控制．文献[15]设计了基于滑模控制的随机时滞系统鲁棒观测器，给出了滑模面及控制器设计的方法，但是针对的是线性连续系统．对于非线性离散系统，文献[16]基于观测器设计非线性切换函数及控制器，对于滑模控制研究有很大的促进意义．但是关于观测器下非线性离散时变时滞系统的滑模控制研究还不够完善．

在前人研究的基础上，本文研究非线性扰动下不匹配不确定离散时变时滞系统的滑模控制问题．构造观测器估计系统，并在此基础上设计离散积分滑模面，采用Lyapunov函数稳定性理论及线性矩阵不等式（LMI）技术，得到系统渐进稳定的充分条件．设计一种基于观测器的滑模控制律，以改善滑模到达条件，并在控制律中引入饱和函数，以消除系统的抖振．

1　系统描述

考虑一类非线性不确定离散时变时滞系统

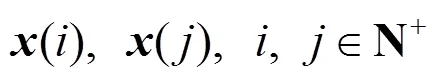
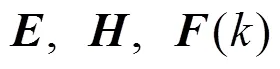
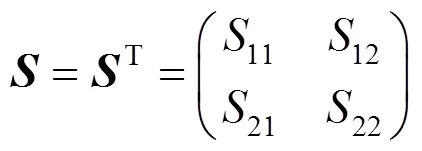
2　观测器设计

由于系统状态不可测，为了估计非线性不确定时变时滞离散系统（1）的状态，设计观测器

偏差系统的输出为

3　滑模面设计与稳定性分析

3.1　构造积分滑模面

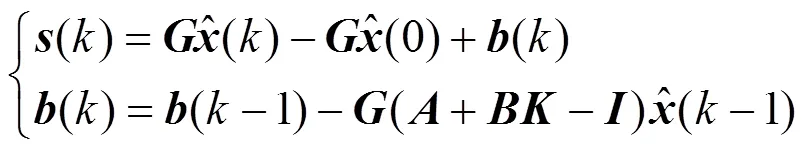
基于式（5），可得

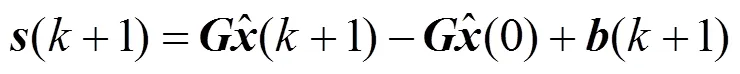
理想的准滑模满足条件

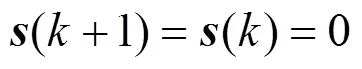
通过式（2），（5），（7）可以得到滑模面上的等效控制

3.2　稳定性分析

分析滑模动态方程（9）的稳定性，并给出保证滑模动态系统渐进稳定的充分条件．

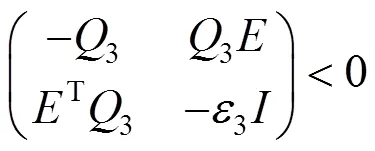
证明构造李雅普诺夫函数

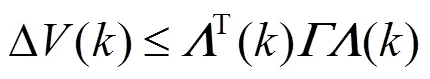
由引理３可知

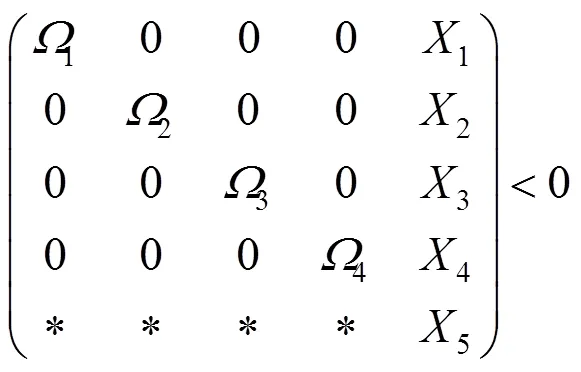
式（16）等价于

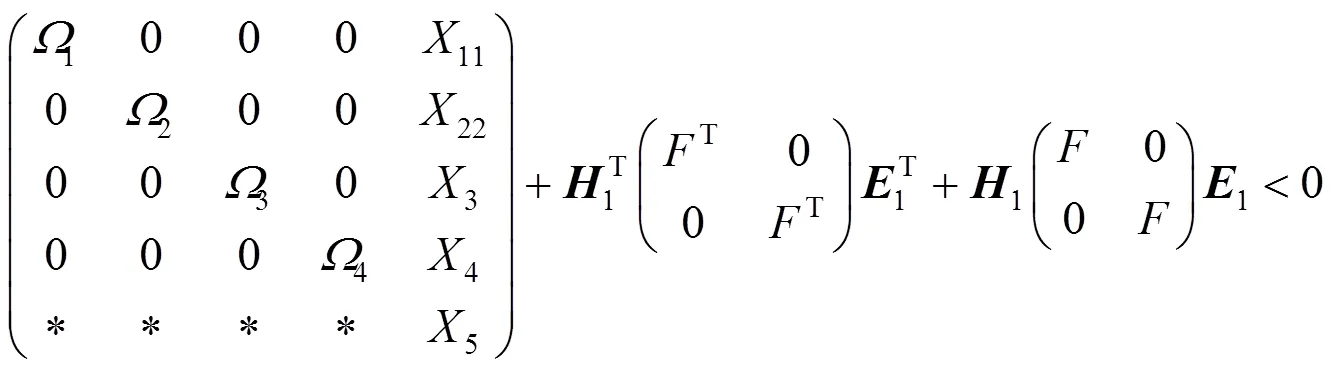
其中：

若

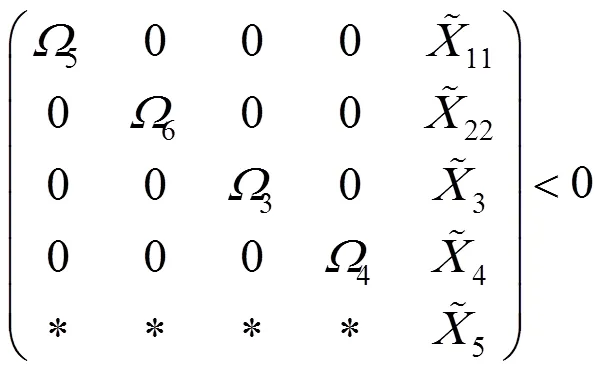
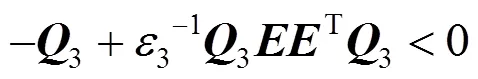
同理，式（18）等价于

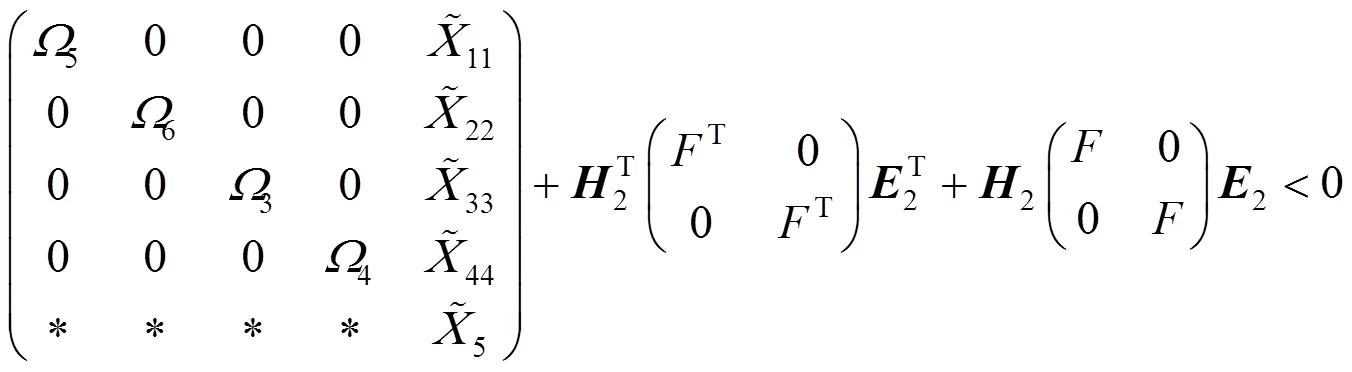
其中：

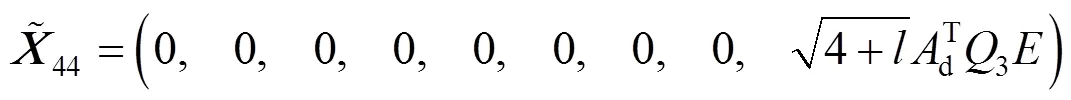
若

3.3　滑模控制律设计

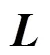
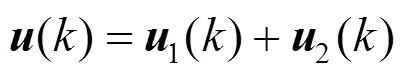
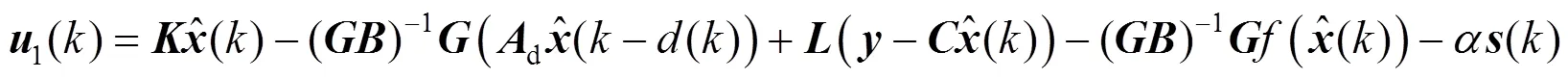
证明 选取Lyapunov 函数为

由滑模函数，可以推导出

因此

把式（24），（25），（28）代入式（29），得到

从而，由式（31）可知

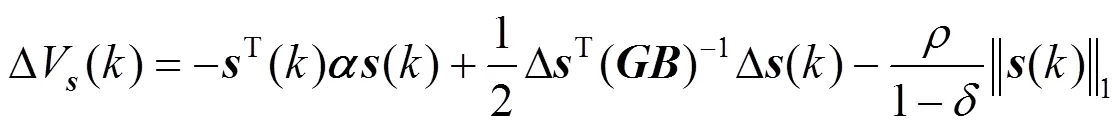
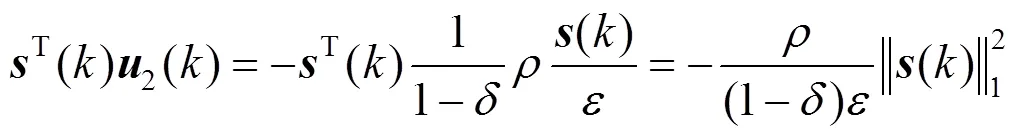
由式（32），（33）可知

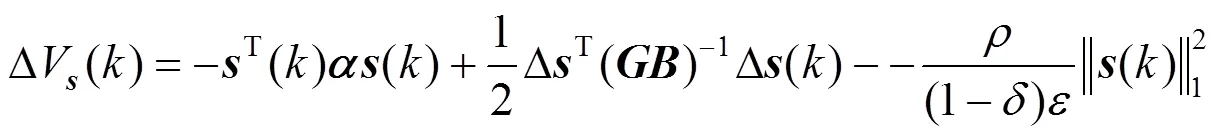
4　数值仿真算例

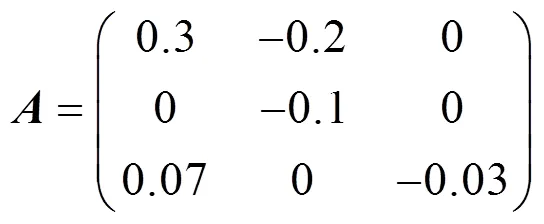
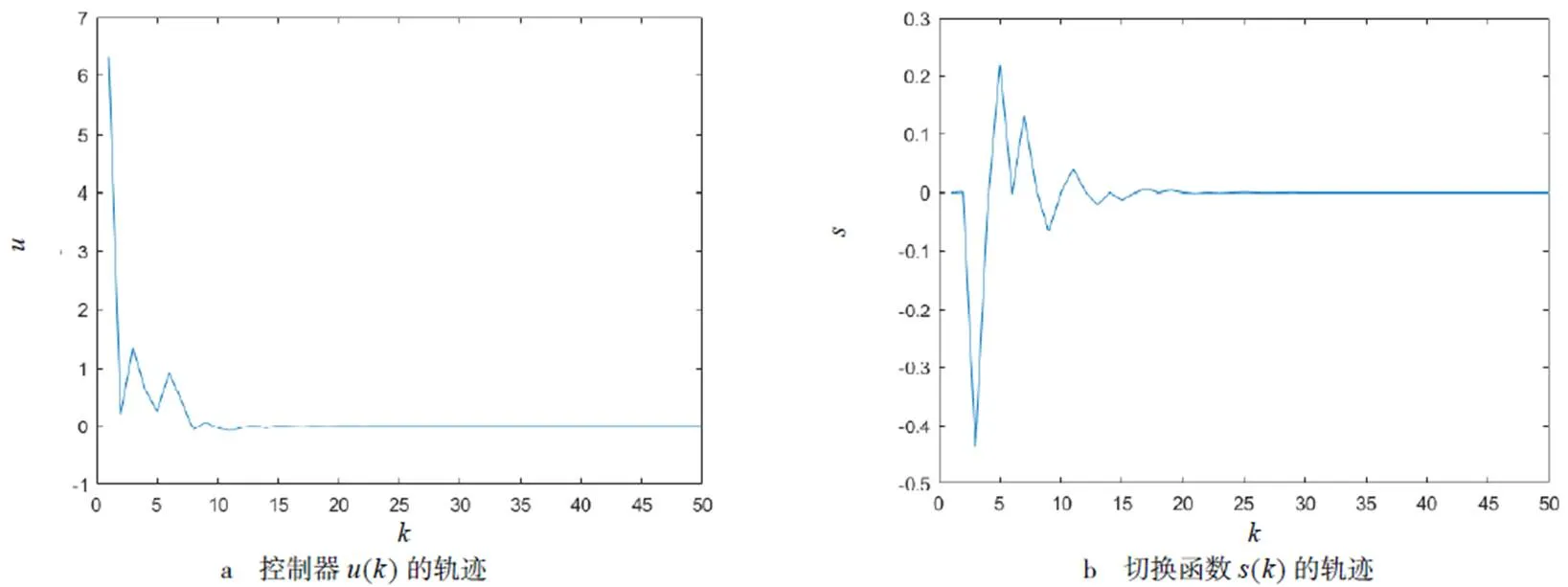
图2　文献[20]控制器的仿真结果

由图1a~f可以看出，估计值均以较快的速度收敛于实际值，系统的状态变量能以较快的速度收敛于零．由图1g~h和图2，通过对比可以得出，本文所设计的控制器收敛速率快大约10%，状态轨迹在控制器（23）的作用下在有限时间内更快到达滑模面并保持在该领域内．

5　结语

本文研究了具有非线性离散不确定时变时滞系统的滑模控制，在状态不可测的情况下，构造观测器来估计系统状态，提出了基于线性矩阵不等式（LIM）技术的积分滑模面设计方法，推导出误差系统和滑模动态方程的零解渐进稳定性的充分条件．根据滑模变结构控制的到达条件设计了积分滑模控制器，有效地削弱不确定性、时滞、非线性干扰等因素的影响，同时抑制了系统的抖振，仿真实例验证了本文所提方法的有效性．本文得出的结果对于滑模控制领域的研究具有一定的价值．

[1] 郑大钟．线性系统理论[M]．北京：清华大学出版社，1990

[2] 刘金琨．滑模变结构控制MATLAB仿真[M]．北京：清华大学出版社，2005

[3] Utkin V I．Sliding Modes in Control and Optimization[M]．Berlin：Springer Berlin Heidelberg，1992

[4] 杨朋松，孙秀霞，董文瀚，等．一类不确定离散时间系统的积分滑模控制[J]．控制与决策，2012，27（9）：1397-1401

[5] 孙娜娜，牛玉刚，陈蓓．一类不确定离散时间系统的最优积分滑模控制[C]//第三十一届中国控制会议，中国自动化学会控制理论专业委员会，合肥，2012

[6] 高为炳．变结构控制理论及设计方法[M]．北京：科学出版社，1996

[7] 高存臣，袁付顺，肖会敏．时滞变结构控制系统[M]．北京：科学出版社，2004

[8] 吴敏，何勇．时滞系统鲁棒控制：自由权矩阵方法[M]．北京：科学出版社，2008

[9] L Xiaoqian，Li J，Chang L．Global sliding mode control for uncertain linear systems with state time-delays[C]//Control Conference．IEEE，Technical Committee on Control Theory，Chinese Association of Automation，北京，2010

[10] 李玮，段建民．非匹配不确定时滞系统的自校正滑模控制[J]．系统工程与电子技术，2011（7）：164-168

[11] Wu L，Ho D W C．Sliding mode control of singular stochastic hybrid systems[J]．Automatica，2010，46（4）：779-783

[12] Nguyen T，Su W C，Gajic Z．Variable structure control for Singularly perturbed linear continuous systems with Matched disturbances[J]．IEEE Transactions on Automatic Control，2012，57（3）：777-783

[13] Han X R，Fridman E，Spurgeon S K，et al．On the Design of Sliding-Mode Static-Output-Feedback Controllers for Systems With State Delay[J]．IEEE Transactions on Industrial Electronics，2009，56（9）：3656-3664

[14] 颜闽秀，井元伟，姜囡．非匹配不确定线性系统离散滑模输出反馈控制[J]．系统仿真学报，2009（16）：55-58

[15] Niu Y，Ho D W C．Robust observer design for stochastic time-delay systems Via sliding mode control[J]．Systems & Control Letters，2006，55（10）：781-793

[16] 袁雪娇，高存臣．基于观测器的不确定离散变时滞系统的稳定性[J]．中国海洋大学学报：自然科学版，2018，48（S1）：209-214

[17] 高存臣，袁雪娇，张彩虹．不确定中立型变时滞系统基于状态观测器的滑模控制[J]．中国海洋大学学报：自然科学版，2019，49（7）：149-154

[18] 孙娜娜．不确定离散时间系统滑模控制研究[D]．上海：华东理工大学，2013

[19] Park J H．LMI optimization approach to asymptotic stability of certain neutral delay differential equation with time-varying coefficients[J]．Applied Mathematics and Computation，2005，160（2）：355-361

[21] Benamor A，Messaoud H．Robust adaptive sliding mode control for uncertain systems with unknown time-varying delay input[J]．ISA Transactions，2018，79：1-12

[23] 高存臣，刘振，任启峰．时滞离散时间系统的非线性准滑模鲁棒控制[J]．控制理论与应用，2013，30（1）：123-130

Integral sliding mode control for nonlinear uncertain discrete time-varying delay systems

ZHANG Miaoqing，JIN Chaoyong，WU Lizhen

（School of Applied Mathematics，Guangdong University of Technology，Guangzhou 510520，China）

Studies the sliding mode control problems for a class of nonlinear uncertain discrete time-varying delay systems，the state observers are constructed to estimate the states of the systems under study，the integrated sliding mode surfaces are designed based on the estimated states to make the entire dynamic procedures possess complete robustness with regard to the external disturbances．Using the Lyapunov stability theories and the technologies of linear matrix inequalities （LMI）， sufficient conditions for the progressive stability of sliding mode dynamic systems are provided．Then，the corresponding sliding mode controllers are designed and the saturation functions are introduced in the controllers to eliminate the chattering of the systems．Some simulation examples are shown to verify the effectiveness of the proposed method．

time-varying delay；uncertainty；discrete time；sliding mode control

O231.2

A

10.3969/j.issn.1007-9831.2020.03.002

1007-9831（2020）03-0010-09

2019-12-22

张妙清（1995-），女，广西玉林人，在读硕士研究生，从事控制理论及应用研究．E-mail：761366752@qq.com