基于PLC对二级随动液压消音器的设计及特性分析
2020-05-22
(昭通学院 物理与信息工程学院, 云南 昭通 657000)
引言
液压泵的脉动式流量输出流经液压管道时会产生压力脉动,压力脉动会造成管道系统的振动和噪音的产生。针对此问题,前人展开了大量研究,通过不同的途径,如改良泵的输出脉动、调整管道参数、增加管道支撑点[1-3]等对液压系统进行消音和减噪。但是在液压系统高压化的进程中,传统消振途径不能满足发展需要,为了解决这一技术难题,人们设计开发出不同种类的液压消音器: H型脉动衰减器、 薄板振动式液压脉动衰减器、多腔体型脉动衰减器等。H型脉动消音器结构简单可靠,KOJIMA等[4]设计出多腔体H型流体脉动衰减器,通过合理设计可使该种衰减器在多个频率段工作,但是此多腔体H型脉动衰减器会在高频率段衰减效果不理想。贺尚红等[5]对薄板振动式液压消音器进行了深入的探讨,结果表明该液压脉动衰减器能在较宽的频率范围内进行降噪。单长吉[6-7]提出了多孔液压消音器,并分析得到二级多孔液压消音器的脉动衰减效果优于一级多孔液压消音器和三级多孔液压消音器;同时研究了质量室为并联管对称分布的液压消音器,证明了二级液压消音器的衰减性能可以替代三级液压消音器。以上讨论的多腔体型液压脉动消音器都是以固定的结构参数来衰减压力脉动,而工程应用实际中液压泵的工作复杂性,迫切需要一种可以改变自身结构参数的多腔体型液压消音器来满足工程液压系统主要脉动频率段的消振。
本研究在静态液压消音器的基础上,加装了一种结构简单紧凑、体积小、通用性强的随动装置,能够及时根据泵的转速的改变来调整液压消音器的结构参数(即用滚珠丝杠带动滑动挡块移动来改变液压消音器结构参数),使得二级液压消音器的2个固有频率分别与液压系统的固有脉动频率和回冲脉动频率相匹配,从而使二级随动消音器达到最佳消振效果。
1 H型二级随动液压消音器的结构参数确定方法与工作原理
1.1 H型二级液压消音器共振频率的确定
从图1可知:液压泵的的压力脉动由1点输入,经过1-2段管路进入容腔Ⅰ;经3-4段管路进入容腔Ⅱ。1-2,3-4两段管路起到液阻的作用,消耗一部分脉动能量。容腔Ⅰ、Ⅱ起到液容的作用,吸收来自2点和4点的流量脉动。因此,H型二级液压消音器具有2个固有频率。当其2个固有频率分别与泵的固有脉动频率与回冲脉动频率相等时,发生共振,此时消音器衰减压力脉动的效果最佳。这就是H型二级液压消音器的工作机理。
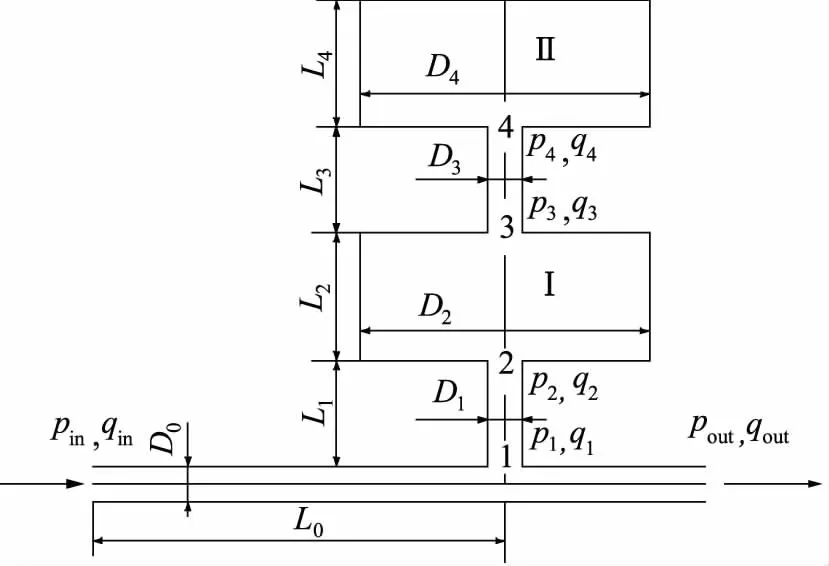
图1 二级液压消音器结构参数图
随动液压消音器的吸收频率设计对于液压系统来说至为重要,杜润等[8]对二级液压消音器进行数学建模,得到其2个共振频率表达式为:
(1)
(2)
式中,L1—— 1-2管路的长度,m
L3—— 3-4管路的长度,m
V2—— 容腔Ⅰ的体积,m3
V4—— 容腔Ⅱ的体积,m3
D1—— 1-2管路的直径,m
D3—— 3-4管路的直径,m
a—— 常数
柱塞泵的固有脉动频率为:
(3)
柱塞泵的回冲脉动频率为:
(4)
式中,nh—— 液压泵的转速,r/min
Z—— 柱塞数
当液压泵的转速改变时,可以根据式(3)、式(4)计算出固有脉动频率和回冲脉动频率,将其分别代入式(1)和式(2),即:f1=f11,f3=f33。以此来求得相应的消音器的结构参数。利用传统数学方法和MATLAB编程来求解二级液压消音器的结构参数存在着相当大的困难。因此,采用半定量方法,结合脉动衰减曲线图,采取逐步逼近法,最终可以确定二级随动液压消音器的结构参数。液压脉动衰减公式如下[9]:
(5)
式中, TL —— 透过损失,dB
pin—— 输入压力,MPa
qin—— 输出流量,m3/s
pout—— 输出压力,MPa
qout—— 输入流量,m3/s
1.2 基于PLC控制的H型二级随动液压消音器的工作原理
图2为基于PLC控制的二级随动液压消音器的结构简图,随动调节装置的工作原理和控制原理为:当液压泵转速改变时,速度传感器把与转速对应的转速信号传递给PLC;PLC自动计算后,将转速信号对应的脉冲数以及脉冲频率传递给伺服控制器;伺服控制器接收信号后传递电压信号给伺服电机,从而控制伺服电机转动圈数与转速;伺服电机接收指令后,通过联轴器带动滚珠丝杠转动,进而将滚珠丝杠的转动转换为工作台的平动,从而实现滑动挡块1和3的精确平动,达到对1-2段(质量室1)、3-4段(质量室2)管路流通面积的控制。在液压消音器其他结构参数不变的前提下,使得二级液压消音器的2个固有频率分别等同于系统的固有脉动频率和回冲脉动频率。

1、11.伺服电机 2、12.联轴器 3、13.左轴承4、14.左固定支撑座 5、15.滚珠丝杠 6、16.螺母7、17.工作台 8、18.右轴承 9、19.右固定支撑座10.滑动挡块3 20.滑动挡块121.液压管路壁 22.液压管路图2 基于丝杠-滑块的二级随动液压消音器结构原理图
图3为滑块挡块与质量室的横截面图,考虑到实际加工方便,将质量室设计成方形体。通过控制滑动挡块的精确平动(即控制b的大小)来控制管路流通面积。
2 基于PLC控制的二级随动液压消音器的特性分析
2.1 二级随动液压消音器的静态特性分析
针对液压泵不断连续改变的转速,二级随动消音器是通过及时改变Δb1和Δb3来改变随动液压消音器的2个固有脉动频率, 从而实现随动衰减压力脉动的功能。
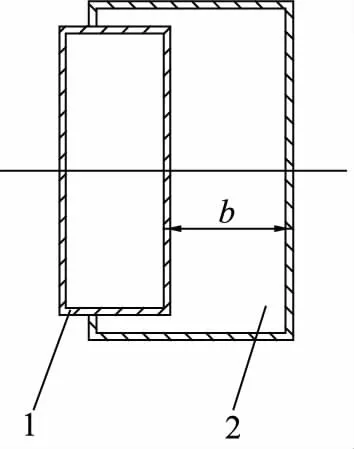
1.滑动挡块 2.质量室图3 滑动挡块与质量室横截面图
1) 精确定位的计算
PLC通过发送的脉冲来控制伺服电机,脉冲频率决定伺服电机转速,脉冲数确定伺服电机转动角度。
图2所示装置简图中:丝杠的螺距为d/m,伺服电机转速为nm/r·min-1,螺纹线数为c,则螺母的位移Δx/m为:
Δx=cdnmΔt
(6)
式中, Δt为丝杠转动时间,s。
伺服电机的分辨率为j/P·R-1,PLC在时间ΔT内发送J个脉冲,则伺服电机转速为:
(7)
将式(7)代入式(6)得:
(8)
由式(6)得:
(9)

(10)
(11)
式中, 下标k(k=1、3)为常数。
2) 实际应用计算和分析
某一9头柱塞泵的最大转速为2200 r/min,以其最大转速的50%(即f1=330 Hz,f3=165 Hz)所对应的滑动挡块位置作为平衡位置,考量转速范围为:50%~100%。选择水作为流体介质。位移与转速变化表如表1所示。以表1作为研究对象得图4、图5。
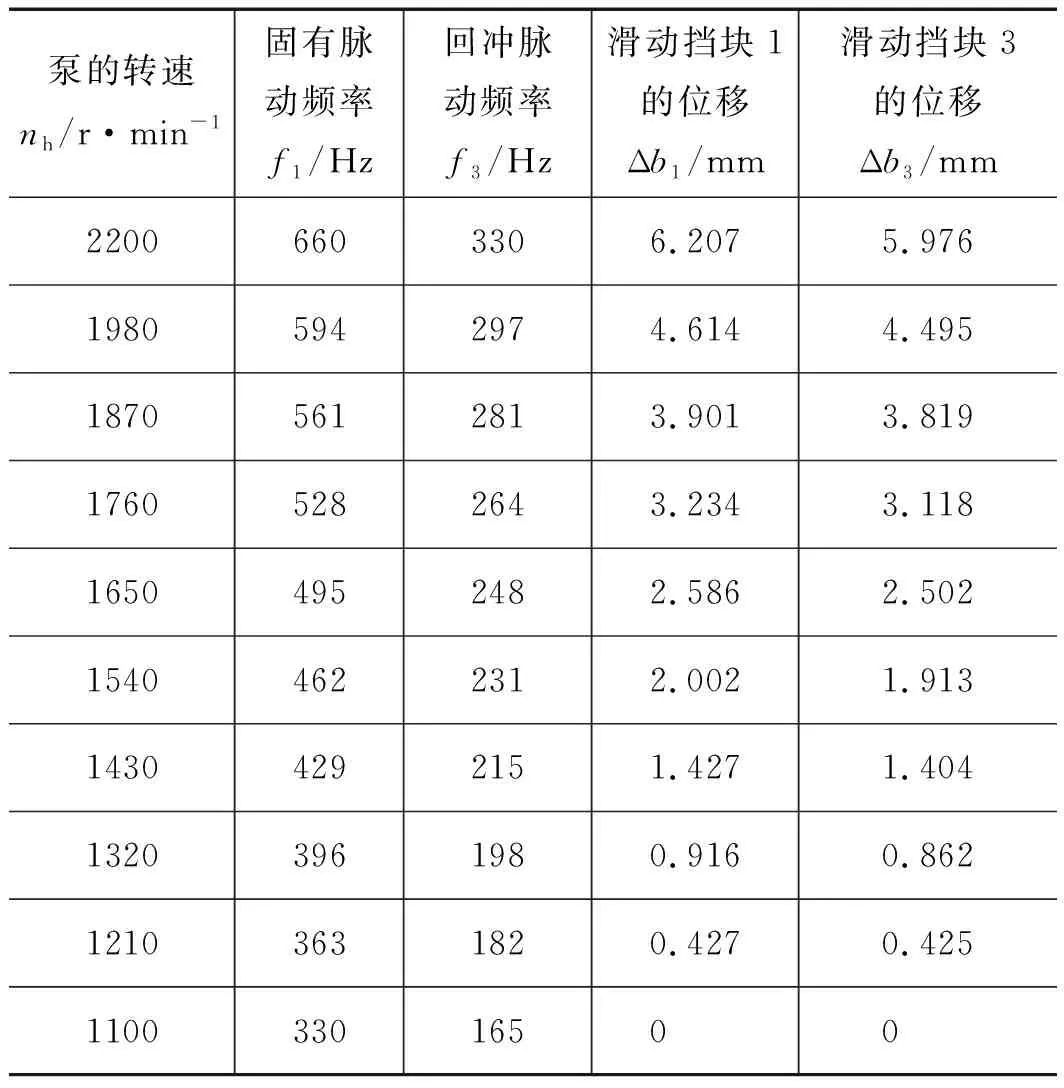
表1 模型结构尺寸表
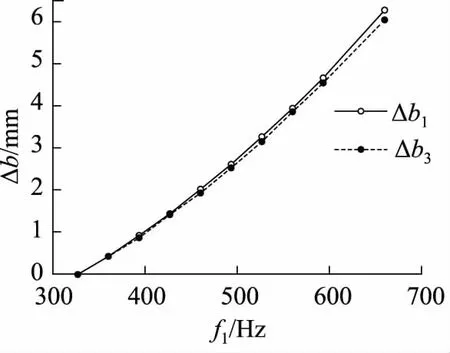
图4 以水为介质,固有脉冲频率与位移图

图5 以水为介质,回冲脉动频率与位移图
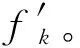

表2 滑块位移Δb1与脉冲信号相关参数表

表3 滑块位移Δb3与脉冲信号相关参数表
从图4,图5中可以看出,以水为介质时,液压系统的固有频率和回冲脉动频率与滑动挡块的位移的关系曲线是幂函数,2种频率的衰减是由2个滑动挡块的位移Δb1和Δb3共同作用的结果,随着频率的增大,位移相差越来越明显。
图6,图7给出了滑动挡块位移和脉冲数的变化图,由图可知,位移与脉冲数成正比例函数。当位移越小时,N1和N3差值越小,反之越大。
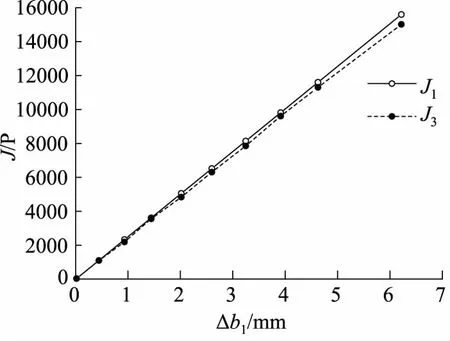
图6 以水为介质,脉冲数J1和J3与位移Δb1图
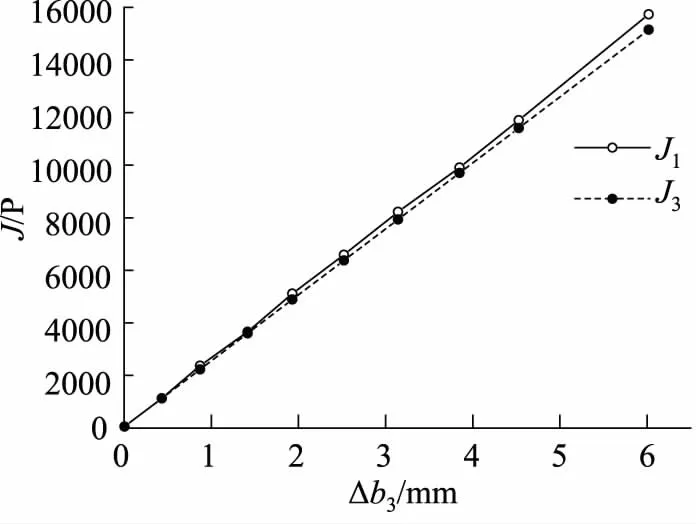
图7 以水为介质,脉冲数J1和J3与位移Δb3图
从图8可以看出,取液压系统的固有脉动频率为528 Hz、回冲脉动频率为264 Hz时,3种介质(水、32号液压油、46号液压油)的频率衰减效果:TL水>TL32号液压油>TL46号液压油。采用电学中的品质因数(Q值)概念,Q水>Q32号液压油>Q46号液压油,即介质为水时,对衰减频率的选择性优于其他2种介质。
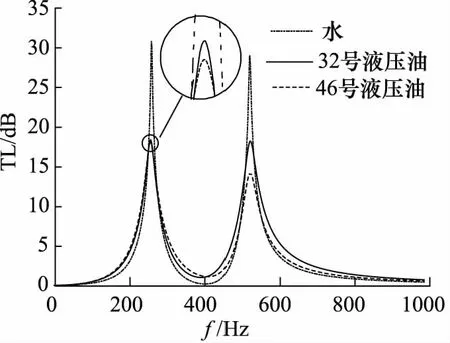
图8 二级随动H型液压消音器对3种介质的脉动衰减比较图
图9为一级H型液压消音器对液压系统的回冲脉动频率(3种介质:水、32号液压油、46号液压油)为264 Hz时的频率衰减效果图。

图9 一级H型液压消音器对3种介质的脉动衰减比较图
比较图8和图9可以得到,二级随动液压消音器对液压系统3种介质的脉动频率的衰减效果优于一级H型液压消音器的衰减效果,并且二级随动液压消音器可以同时衰减回冲脉动频率和固有脉动频率,而一级H型液压消音器只能衰减其中的一种频率。
2.2 随动调节装置的动态特性分析
由二级随动消音器的静态特性分析可得,液压泵的转速改变时,需要及时改变二级随动液压消音器的结构参数。但是二级随动调节装置的滚珠丝杠在转动时,受到工作台的作用,不可避免地会产生振动[10],滚珠丝杠的振动对二级随动液压消音器的工作性能的影响不可忽视。因此,研究滚珠丝杠的动态特性[11-13]对随动装置的影响是保证二级随动液压消音器工作可靠的前提。
1) 滚珠丝杠的动力学方程
将滚珠丝杠简化为受移动力作用的修正Timo-shenko梁[14]来进行研究。常系数修正Timoshenko梁的运动方程包含一个2阶和一个3阶的偏微分方程,如式(12)、式(13)所示:

(12)
(13)
式中,S—— 梁的横截面积,m2
G—— 梁的切变模量,MPa
μ—— 剪应力不均匀系数
w(x,t) —— 梁横截面的挠度,m
φ—— 梁横截面的转角,rad
E—— 梁的弹性模量,MPa
I—— 梁横截面对中性轴的惯性矩,m4
f(x,t) —— 作用在梁上的分布载荷,N/m
由式(12)、式(13)消去φ得梁受激励力的振动方程为:
(14)
2) 梁的自由振动的求解
令f(x,t)=0,由式(14)可得梁的自由振动方程为:

(15)
引入下列无量纲[15]常数及参数:
式中,l为梁的长度,m。
将式(16)代入式(15)式得梁的无量纲自由振动方程为:
(17)
可采用分离变量法求解梁的无量纲自由振动方程。令:
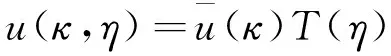
(18)
将式(18)代入式(17)式得:
(19)

将式(19)的通解还原其无量纲参数可得修正Timoshenko梁的自振频率计算公式为:
(20)
根据欧拉待定系数指数函数法求解方程式(19)的解,得出其特征方程的4个特征值为:
令:
A1,2=±θ,A3,4=±ib
(21)
式(21)的4个特征值对应4个线性独立的解,由此可得方程(19)式的通解为:
(22)
式中,Cm(m=1,2,3,4)为积分常数。
式(22)即为梁的振型函数,积分常数Cm由梁的边界条件确定。
3) 由梁的边界条件求解梁的自振频率
由于横向外部激励不会影响梁的固有频率,所以求解固有频率时可撤去外部激励。列出简支梁的边界条件为:
(23)
将式(23)分别代入式(21)、式(22),整理得:
b=nπ(n=1,2,…,n)
(24)
(25)
对应的固有频率为:
(26)
滚珠丝杠的物理参数如下:
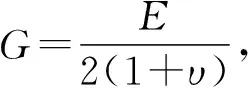
引入修正Timoshenko简支梁的固有频率公式[16]:
(27)
由式(26)及式(27)自振频率公式分别计算滚珠丝杠的固有频率。表4给出了丝杠的前五阶固有频率,从表中可以看出,2种方法算出的固有频率是一致的,说明推导出的固有频率公式(26)是正确的。由于采用的滚珠丝杠长度很短(l=40 mm),高跨比大,故求出来的固有频率大。由于工作台的运动频率远小于第一阶固有频率,所以丝杠与工作台在运动中不会发生共振现象。
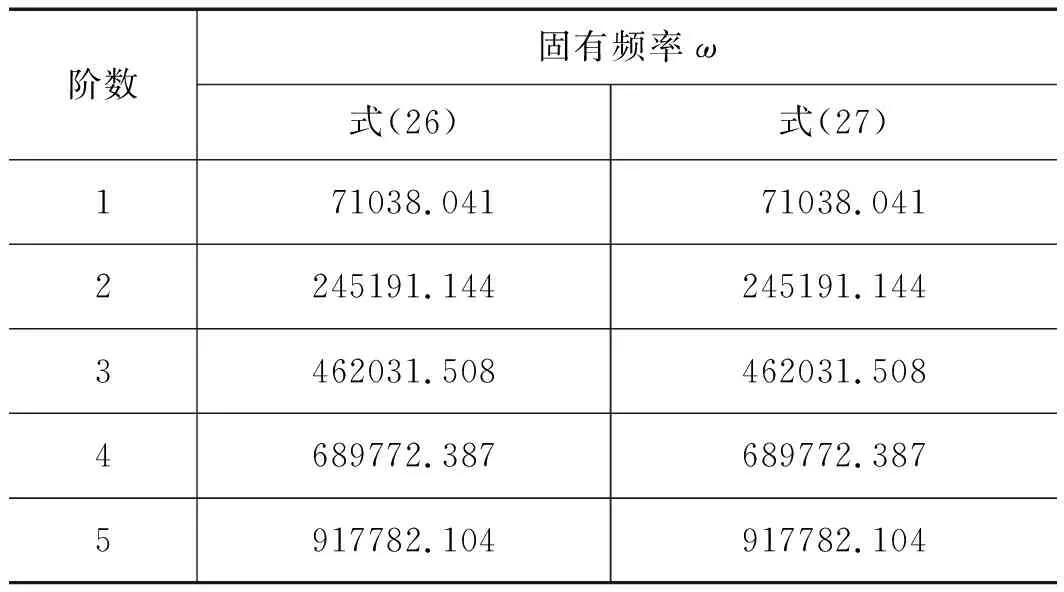
表4 滚珠丝杠的前五阶固有频率表 Hz
2.3 滚珠丝杠对激励的响应[17]
设工作台以速度v在丝杠上运动,忽略工作台的惯性,可简化为集中力F=mg沿丝杠移动,如图10所示。
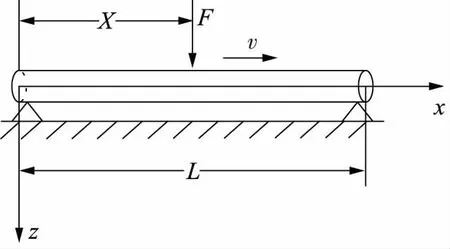
图10 丝杠受力简化图
丝杠的振动可用集中荷载作用下各阶振型的线性组合表示:
(28)
将式(28)分别代入式(14)、式(15),整理得:

(29)
由文献[16]导出简支修正Timoshenko梁的正交条件为:
(30)
引入参数Mn、Qn,分别定义为:
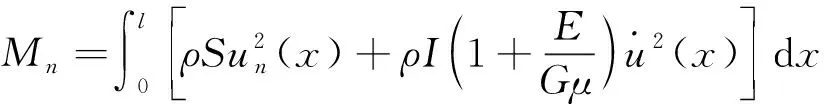
(31)
(32)
将式(29)各项与uk(x)相乘后沿梁的全长积分,利用正交条件式(30)以及式(31)和式(32)得:
(33)
利用杜哈梅积分得出式(33)的解的一般形式为:
(34)
集中力载荷可利用脉冲函数关系表示为:
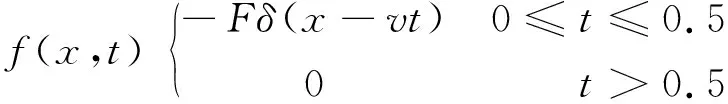
(35)
式中,F为工作台的重力,N。
令初始条件为0,将振型函数简正化后和式(34)、式(35)一起代入式(28)得:
(36)
式(36)为受到激励力简支梁的挠度方程。本研究设计的二级随动装置工作台和螺母质量为1.02 kg,工作台的平均速度v=0.08 m/s;将随动装置的结构参数代入式(36),利用MATLAB编程,得到图11~图13。
图11是以滚珠丝杠的有效行程为研究对象(x=40 mm)的振幅随时间变化的三维立体图。从图中可以看出,在工作台移动过程中,滚珠丝杠的挠度在任意时刻的最大值在丝杠的中点(x=20 mm)处,振幅最大值发生在t=0.25 s时刻。
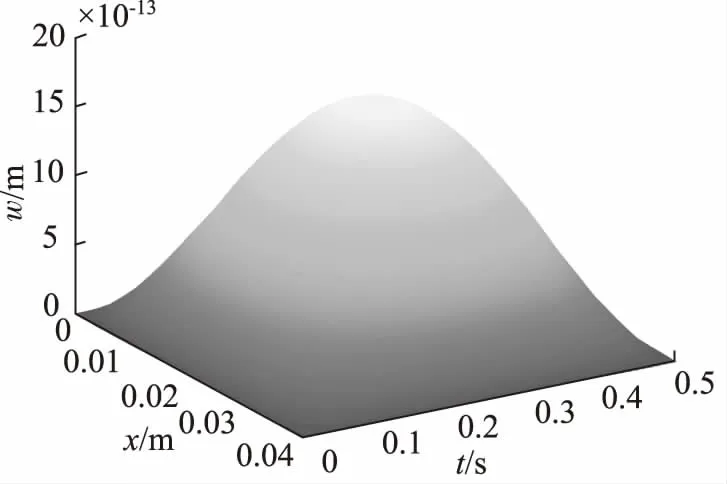
图11 滚珠丝杠挠度的三维立体图
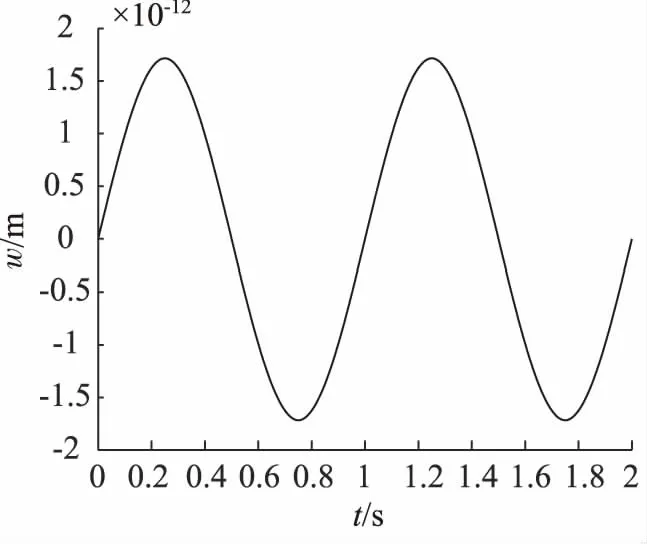
图12 滚珠丝杠中点振动时间变化图

图13 丝杠工作振动时间变化图
图12为丝杠的振幅最大值随时间变化的平面图。由图可知,t=0.25 s时,工作台位于x=20 mm处,振幅最大值为wmax=1.72×10-12m;振幅振动的数量级达到10-12m级别,可以认为其不会对随动装置运行的稳定性产生不良影响。
图13是工作台移动以及工作台移动完成后滚珠丝杠的振动随时间变化的三维图。从图中可以看出,工作台停止移动后,丝杠的自由振动与受激振动相差非常小。所以,二级随动调节装置在实际工作时,丝杠的振动可近似简化为t=0.5 s后的自由振动。结合图12,表明二级随动液压消音器工作时非常稳定,符合工程实际。
通过以上对二级随动液压消音器的动态性能计算与分析,可以得出:本研究设计的二级随动液压消音器能够响应及时、运行平稳、达到工程设计的要求。
3 结论
(1) 设计了一种新型的二级随动液压消音器,将消音器的结构参数随泵的转速的变化而改变,可以对不同时刻的回冲脉动频率和固有脉动频率进行衰减;
(2) 综合分析了装置的静态特性和动态特性,推导得到了脉冲数和滚珠丝杠振动的挠度函数表达式,并在此基础上分析了装置的滚珠丝杠振动带来的影响,分析结果表明滚珠丝杠的振动带来的影响非常小,可以忽略不计;
(3) 改进后的二级随动液压消音器系统运行稳定,能够实现同时对液压系统中的固有脉动频率和回冲脉动频率的即时衰减。为工程动力装置降噪提供了一种途径,在结构设计上提供了一种理论参考。
