三个二次巧转化,数学问题妙求解

一元二次不等式与其对应的二次函数、一元二次方程三者之间存在着密切的联系。同学们在解决相应的数学问题时,要充分注意三个“二次”之间的相互联系,并在一定条件下可以相互转换与应用。数形结合思想是解决二次方程、二次函数和二次不等式问题中的重要数学思想之一,具体解题时,要充分利用图像的直观性反映相应问题的本质,重视用函数观点处理相应的方程或不等式问题。

1.二次方程的转化

在解决二次方程的根的存在、根所在的区间等问题时,利用二次方程所对应的二次函数的图像与性质来转化,综合相应不等式(组)的求解来达到分析与求解的目的。

例1已知关于x的一元二次方程x2+2mx+2m+1=0有两个根x1,x2,其中x1∈(-1,0),x2∈(1,2),求m的取值范围。

解析：设f(x)=x2+2mx+2m+1,根据题意,画出示意图如图1 所示,由图可得,m满足不等式组解得

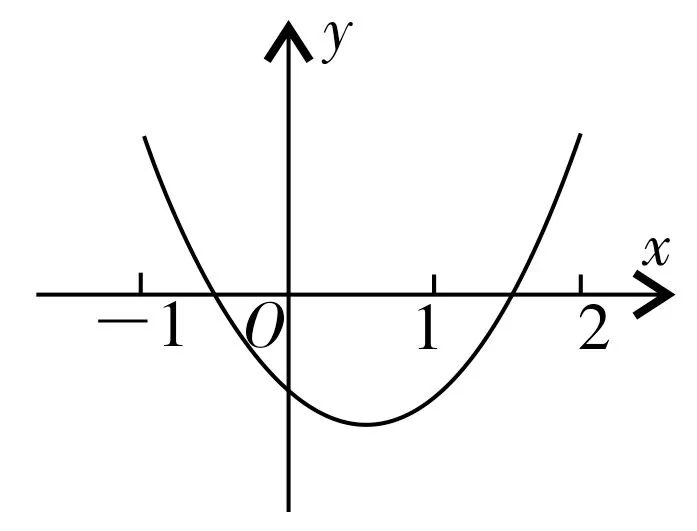
图1

2.二次函数的转化

同学们在解决二次函数的解析式、确定二次函数的图像等问题时,可把问题转化为与之相关的方程根的分布问题、不等式的求解问题,结合数形结合思想,通过函数、方程与不等式之间的相互关系,巧妙转化,达到求解的目的。

例2已知二次函数f(x)=mx2-2mx-1(m≠0),若 对 于x∈[1,3],函 数f(x)的图像恒在y=-2m+4的下方,求实数m的取值范围。

解析：由题意可知f(x)＜-2m+4 在[1,3]上恒成立,则mx2-2mx+2m-5＜0,即m(x-1)2+m-5＜0 在x∈[1,3]上恒成立。令g(x)=m(x-1)2+m-5,x∈[1,3]。

当m＞0 时,g(x)在[1,3]上是增函数,所以g(x)max=g(3)=5m-5＜0,解得m＜1,则0＜m＜1;

当m＜0 时,g(x)在[1,3]上是减函数,所以g(x)max=g(1)=m-5＜0,解得m＜5,结合条件可得m＜0。

综上可知,实数m的取值范围是{m|m＜0 或0＜m＜1}。

3.二次不等式的转化

对于一元二次不等式的恒成立问题,往往根据相应的二次函数图像与x轴的交点情况来确定对应的判别式的符号,以及结合一元二次方程的根、判别式公式等来转化,进而解决相应的恒成立问题。

例3试问是否存在实数m,对x∈R,不等式mx2-2x-m+2＜0 恒成立? 若存在,则求出实数m的取值范围;若不存在,请说明理由。

解析：若不等式mx2-2x-m+2＜0恒成立,则知函数f(x)=mx2-2x-m+2的图像全部在x轴的下方。当m=0时,原不等式可化为2-2x＜0,解得x＞1,不满足题意x∈R;当m≠0时,此时函数f(x)=mx2-2x-m+2为二次函数,则需满足二次函数的图像开口向下且相应的二次方程mx2-2x-m+2=0无解,则有此不等式组的解集为空集,即m无解。综上可知,不存在这样的实数m使得不等式mx2-2x-m+2＜0恒成立。