基于微分平坦与MPC的智能车换道控制算法

白成盼，惠 飞，景首才

(长安大学 信息工程学院，陕西 西安 710064)

0 引 言

随着车辆数量的不断增加，越来越多的交通事故发生，其中大多数是由于驾驶人员操作不当造成[1]。研究表明，由于车辆换道引发交通事故的可能性有4%～10%，同时10%的道路堵塞和延迟由换道车辆造成[2]。智能车辆能够准确检测周围车辆的实时动态信息，并通过有效的控制方法实现车辆的自主驾驶，提高交通安全和控制效率。

目前，智能车换道的控制算法有很多。在轨迹规划方面，文献[3]将车辆表示为多个以车身宽度为直径的动态圆，实现车辆的碰撞检测，并利用多项式方法实现车辆换道的轨迹规划；文献[4]将轨迹规划问题转化为对变道时间和变道距离约束的优化问题，为正常变道、紧急变道和超车变道规划参考轨迹；文献[5]将路径局部最小曲率变化作为约束条件，利用弹性带理论对车辆紧急路径进行规划，提高了车辆的操纵稳定性；文献[6]提出了一种基于环境识别的自动变道算法，利用车载传感器检测多种信号，并对变道后的本车与周围车辆的最终位置进行估计；文献[7]针对运动开始瞬间的轨迹规划问题，将障碍物表示为简化的s-topes，利用五次多项式结合动力学约束条件求得优化轨迹。在跟踪控制方面，文献[8]提出基于机器视觉和模糊控制的方法实现智能车辆驾驶轨迹跟踪控制；文献[9]利用滑模控制方法计算车辆的行驶速度和横摆角速度进而实现跟踪目的。

模型预测控制(MPC)能够有效克服模型精度误差等不利因素，保证被控对象具有良好的稳定性，因此被广泛应用于智能车控制领域。文献[10]利用MPC设计了一种主动转向控制器，使车辆在满足约束条件的情况下对目标轨迹进行跟踪；文献[11]基于行车环境势场建模与车辆动力学建模，利用MPC的优化控制算法生成最优参考轨迹，在实现轨迹规划的同时进行跟踪控制。

文中将微分平坦理论和模型预测控制算法相结合，提出了一种安全高效的换道轨迹规划和跟踪算法并对其进行验证。

1 智能车换道轨迹规划

由于一次性的轨迹规划计算量大且不易实现，因此文中利用路径-速度分解的方法对智能车实现换道轨迹规划。对智能车辆换道行驶轨迹的生成，按照现有的道路线形条件规划出一条适合其行驶的轨迹，然后根据轨迹上的点来引导智能车辆行驶，同时轨迹规划曲线的平坦性保证了智能车辆轨迹生成的可执行性。结合车辆行驶状态的各项约束求解得到满足车辆行驶目标的sigmoid函数，将其作为控制算法中的全局参考路径；同时，利用微分平坦理论，构造目标优化函数进而对车辆的行驶速度进行规划。

1.1 路径规划

车辆在行驶过程中的路径规划需要满足安全约束、曲率连续约束以及侧向位移约束等条件，sigmoid函数本身具有曲率连续的性质，且满足侧向加速度约束。因此文中提出在sigmoid函数的基础上实现对智能车的轨迹规划算法，其安全换道路径曲线如图1所示。

图1 基于sigmoid函数换道曲线

图中O为被控车辆，L为被控车行驶过程中的障碍车辆。sigmoid函数表达式为：

其中，x,y为车辆的纵向和侧向位移；k为纵向比例增益，表示车辆安全行驶的最大侧向偏移；a,b分别表示从源车道换至目标车道之间过渡轨迹中心的水平偏移量和陡度参数；c为侧向偏移量，根据仿真需求设计。通过求解下列约束方程即可获得满足车辆安全行驶的参考路径曲线参数a,b,c,k：

(1)安全距离约束。

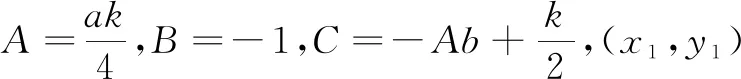
(2)起始点车辆侧向位移约束。

其中，ymax是车辆初始时刻最大侧向位移。

(3)车辆最大侧向加速度约束。

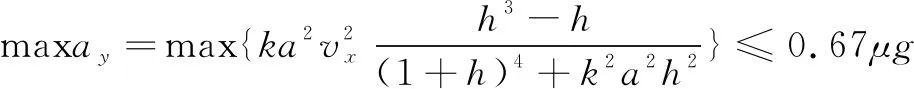
在侧向位移k=3.5 m换道工况下，对上述约束进行求解即可得到任意两点之间光滑且可微的sigmoid函数，可将其作为一项平坦输出进行速度规划，其路径曲线如图2所示。

图2 换道路径曲线

1.2 速度规划

依据智能车辆运动学模型微分平坦性质，运用多项式参数化曲线进行轨迹生成，这种方法只需变换曲线的参数就可以实现车辆不同的轨迹规划行为，从而使智能车辆轨迹规划更具实时性、灵活性。

如果一个系统能够找到平坦输出，使得系统的输入和状态可以由平坦输出及有限微分项表示出来，这样的系统称为平坦系统[12]。利用微分平坦实现轨迹规划既可以降低规划空间的维数同时也能保证规划处的轨迹对系统的可执行性[13]。利用微分平坦进行轨迹规划具体步骤如下：

(1)确定平坦输出：利用微分平坦进行轨迹规划的核心部分就是平坦输出的选定。文中将z=[x,y]作为平坦输出，利用其表示车辆系统运动学模型的表达式为：

对于该模型，u=[v,δ]为控制输入，具体平坦输出表示如下：

(2)平坦输出参数化：轨迹是输入和状态关于时间的函数，因此，将平坦输出变量参数化为适当的时间函数，可以确保产生参考轨迹的可行性。由于sigmoid函数自身曲率连续且满足侧向加速度约束的特点，文中利用简单多项式与sigmoid函数结合，将系统平坦输出参数化为：

(3)轨迹生成。

对上述平坦输出进行参数化后，需要对某一系统性能指标进行优化求解得到一组对应的系统参数，从而获得满足约束条件的轨迹参数作为目标平坦输出轨迹。文中对智能车行使时间以及能量函数进行目标优化，使其在最短的时间内完成高效的换道运动。具体目标函数及约束条件如下所示：

在一般情况下，非线性规划问题只能对其计算解析解，因此，需要将无限维的优化问题进行有限离散化，常用的离散化方法将优化时间域N等分，在N+1个离散点上对状态、控制输入和路径等进行约束。然后利用非线性规划算法求解最优参数，得到满足约束的最优轨迹。将得到的平坦输出直接带入车辆模型中，可以得到对应的控制输入u=[v,δ]，控制智能车速度和转向完成换道。本次微分平坦非线性优化求解得到最优时间tf=19 s，其横纵向加速曲线如图3所示。

从图中可以看出，求得的优化轨迹其加速度均在其约束范围之内。由于微分平坦理论控制车辆是一个完全离线操作的过程，实时性较差，因此文中选择模型预测控制算法对智能车进行在线实时轨迹跟踪实现换道。

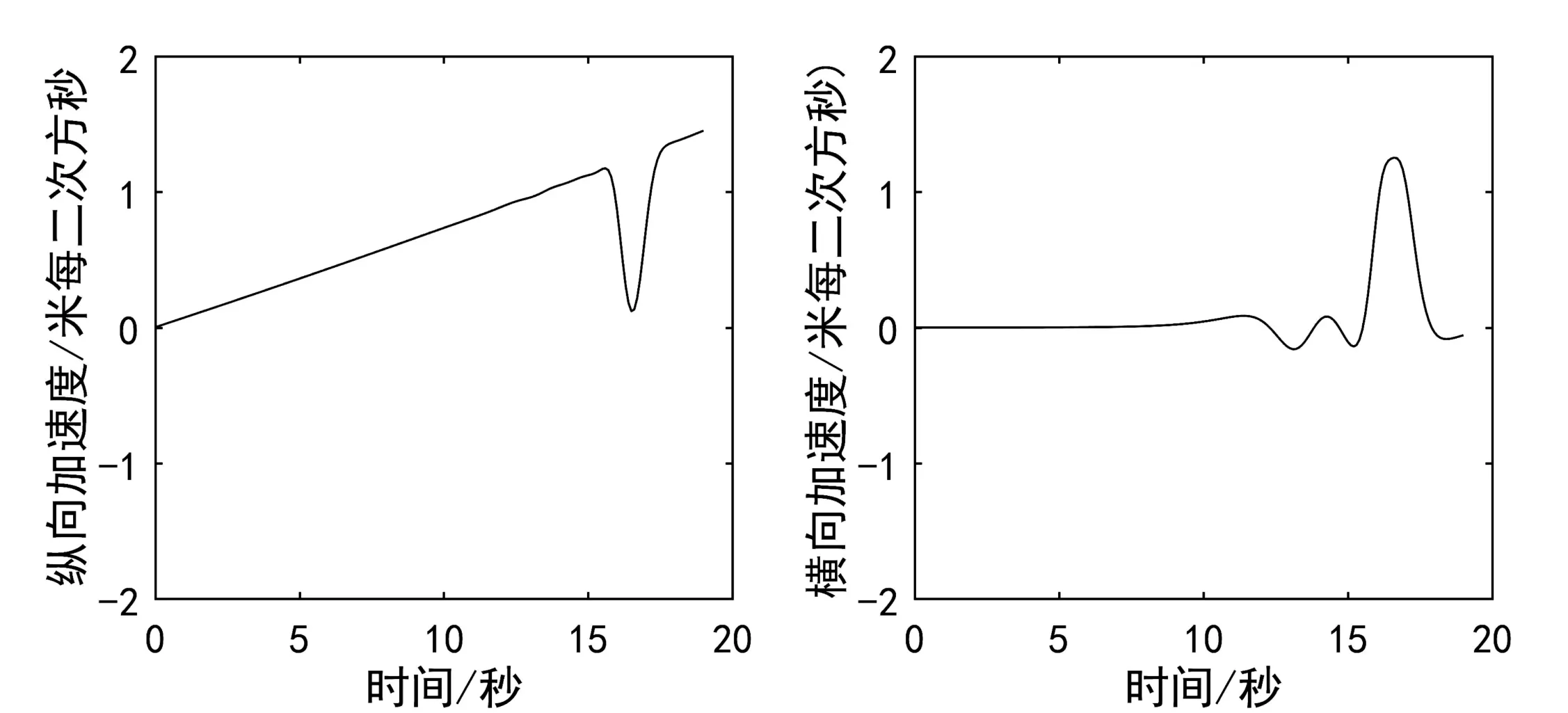
图3 加速度曲线

2 智能车换道轨迹跟踪

在上一节中，利用微分平坦理论只需经过简单的微分和函数运算即可得到期望的智能车换道状态轨迹和控制输入轨迹，方便对其是否满足约束条件进行检验。为满足智能车换道控制系统的实时性，本节将利用动力学模型构造目标函数以实现智能车换道的轨迹跟踪控制。

动力学模型作为对车辆系统动态分析的数学模型，其中典型的三个自由度的车辆模型与车辆运动学模型相结合，详细反映了车辆各项状态变量之间的非线性关系[14]，该模型具体表达式如下所示：

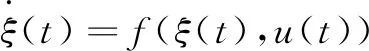
ξ(t+1)=ξ(t)+T·f(ξ(t),u(t))

模型预测控制的核心就是对优化问题的求解，其主要组成部分有目标函数和约束条件，前者确保对自主车辆控制的某些特性需求，后者则主要是对控制量或控制增量等进行附加约束。由于微分平坦中选择的平坦输出[x,y]均是对时间函数的参数化，为实现对智能车的有效跟踪，利用模型预测控制算法设计如下目标函数：

其中，各项分别表示预测时域(Np)内被控车的实际纵向与侧向轨迹和参考轨迹之间的偏差；控制时域(Nc)内对控制增量的要求；第四项中ε为松弛因子，它可以保证在优化求解过程中不会出现没有可行解的情况[15]；Q,S,R,ρ分别为各项权重系数。另外，对控制量和控制增量加以适当的约束能进一步确保车辆稳定行驶。

在每个优化求解周期内将得到的控制序列中首个元素作为实际的控制输入并作用于CarSim整车系统继而进行下次循环，直到完成换道。

3 算法验证结果分析

本节利用车辆动力学仿真软件CarSim与MATLAB/Simulink联合仿真对提出的轨迹规划算法进行验证。

实验场景中所涉及的车辆使用CarSim整车模型，具体模型参数见表1。文中将微分平坦优化得到的平坦输出轨迹带入到S函数中结合模型预测控制对被控车进行跟踪控制，对轨迹规划算法完成验证，具体Simulink仿真图如图4所示。

表1 车辆模型参数

图4 Simulink仿真图

场景中车道宽度为3.5 m，将第一节中得到的具有安全性的sigmoid函数作为参考路径进行换道，结合微分平坦求解得到的系统输入对被控车的速度进行实时控制，安全高效地完成换道。在轨迹跟踪过程中，模型预测控制器的参数设置如表2所示。

表2 控制器参数设置

在仿真过程中，将规划层中利用约束求解以及微分平坦得到满足加速度约束的路径曲线和参考速度作为下层跟踪控制的参考，利用表2参数对提出的代价函数进行优化求解，从而将求解得到的前轮转角输出至CarSim整车模型以实现车辆的换道控制。经验证，智能车在换道场景中的行驶轨迹和速度曲线(a)、航向角与前轮转角变化曲线(b)、实际跟踪轨迹与参考轨迹的位移偏差(c)如图5所示。图6为Carsim仿真动画效果截图，可以直观地反映车辆在换道过程中的7个时刻的状态。结合图5、6可以看出，控制参数转向角在约束范围之内，同时其轨迹跟踪误差极小，证明了该算法有效。

(a)轨迹和速度曲线

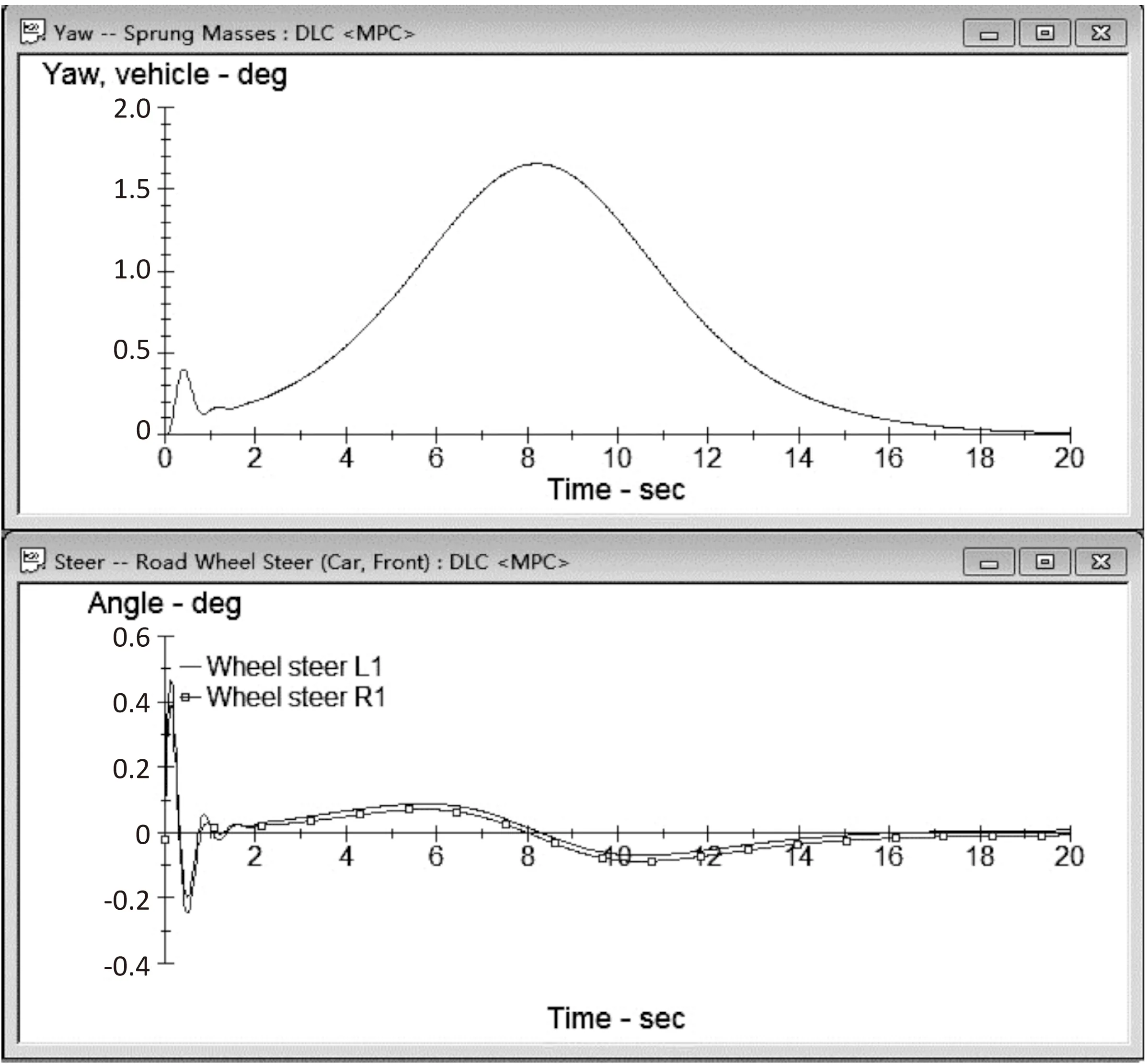
(b)航向和前轮转角曲线

(c)位移偏差

图6 Carsim仿真动画

4 结束语

针对智能车换道安全控制问题，提出了一种基于sigmoid函数与微分平坦理论相结合的换道轨迹规划算法，并利用基于车辆动力学模型预测控制算法对智能车参考轨迹进行跟踪控制，使其能够及时有效地完成换道。相较于其他轨迹规划的算法，系统的微分平坦特性和全状态反馈线性化特性是等价的，因此，在轨迹规划过程中会完全再现系统的动力学特性；sigmoid函数本身的优越性质加上微分平坦理论简化了整个系统的复杂性，同时经仿真验证，该算法适用于对智能车换道行为的轨迹规划。