基于神经网络的混合数据的因果发现
2020-05-22耿家兴万亚平李洪飞
耿家兴,万亚平,2,李洪飞
(1.南华大学 计算机学院,湖南 衡阳 421001;2.中核集团高可信计算重点学科实验室,湖南 衡阳 421001)
0 引 言
随着机器学习、深度学习等人工智能算法的崛起,人们逐渐意识到不能单纯地关注数据的相关性。2011年图灵奖得主Judea Pearl[1]认为人工智能深陷关联概率的泥潭从而忽视了因果,同时Judea Pearl认为研究者应该研究因果,因为这可能是实现真正的人工智能的可能路径。随着因果推断的深入研究,基于因果推断的应用也越来越多,例如在fMRI数据上的分析和分子发现途径研究;Statnikov等人[2]在2012提出了基因组学数据中因果分子相互作用的鉴定方法;Ma Sisi在2017年的工作中讨论了生物医学中观察数据可用于因果发现[3],以及在网络性能优化[4]、网购服装推荐[5]、社会媒体应用等[6]领域都有相关应用。因此因果推理正在成为机器学习领域一个越来越受关注的研究方向。现阶段的因果发现主要是在不进行任何干预的情况下确定两个变量之间的因果方向,这是一项具有挑战性的工作。在近阶段的因果发现研究进展中允许在某种假设下,基于纯粹观察数据推断两个变量之间的因果方向。然而在现实世界中观察到的数据往往由多种生成方式产生,这使得传统的因果推断方法存在识别率不高和稳定性较差的现象。
1 相关工作
目前在二元变量上的因果推断方法主要有两种,第一种是基于时序数据的因果方向推断,第二种是基于非时序数据的因果关系发现,现阶段研究比较多的是基于非时序数据的因果推断。
非时序数据上的因果关系发现又分为基于统计分析的因果推断和基于模型假设的因果推断。基于统计分析:Kano等人[7]于2003年提出路径分析法用于观测数据的因果结构,该方法通过将隐含协方差矩阵与样本协方差矩阵进行比较,对假设的因果关系进行统计检验,从而得出假设的因果关系的正确性。2003年Comley[8]提出了一种对称贝叶斯网络通过使用一种简单的决策树算法能够很好地识别连续型和离散型的联合概率分布。Sun等人[9]于2006年提出一种使用马尔可夫核函数来选择多变量之间的所有假设因果方向中的最可能的一个方向。基于模型假设:Shimizu[10]在2006年提出了一种线性非高斯非循环模型LinGAM,该算法假设数据是线性非混淆的,同时干扰变量是非高斯的,该模型使用独立成分分析的方法来进行因果分析。Zhang等人[11]在2009年通过考虑原因的非线性效应,内部噪声效应和观测变量中的测量失真效应,提出了后非线性因果模型PNL,并证明了该方法在因果方向的可识别性。在2009年Hoyer提出[12]加性噪声模型ANM,该模型能够处理非线性的数据,并成为了一种常用的因果发现方法。Janzing等人[13]提出通过二阶指数模型定义一系列平滑密度和条件密度,即通过最大化受第一和第二统计矩影响的条件熵来识别包含离散变量和连续变量的因果结构。2010年Daniusis等人[14]提出一种确定两个可逆函数相互关联性来识别确定的因果方向。2011年Jonas[1]提出了利用加性噪声模型对离散型数据的因果推断算法。2012年Janzing[15]提出了IGCI算法,该算法通过信息空间中的正交性来定义独立性的方法描述因果变量值之间的边缘概率分布和条件概率分布,从而通过因果关系的不对称性来确定因果方向。2015年Sgouritsa等人[16]提出了无监督的高斯回归过程来估计因果变量之间的条件概率CURE算法。2016年Mooij等人[17]总结了使用观测数据区分因果关系的方法和标准。2017年Marx等人[18]采用了一种基于柯尔莫戈罗夫复杂度的信息论方法,并利用最小值描述长度原理提供了一种实用的因果关系发现方法SLOPE。以上这些方法在进行二元变量的混合数据的因果推断中表现较差,2018年Hu[19]提出了一种基于加性噪声算法的混合数据的因果推断方法ANM-MM(additive noise model-mixture model)模型。
ANM-MM模型可以处理二元变量的混合数据的因果推断,但是在求解分布参数的过程中没有考虑到结果变量对分布参数的影响。因此文中在ANM-MM模型的基础上提出了一种使用神经网络学习改进的目标函数从而得到分布参数,原ANM-MM模型的目标函数被看作是该目标函数的一种特例。
2 预备知识
2.1 模型假设
文中提出的方法是在ANM-MM模型的假设下进行的,ANM-MM模型的定义是连续性变量X和Y由有限ANM模型生成,如图1所示。

图1 ANM_MM模型
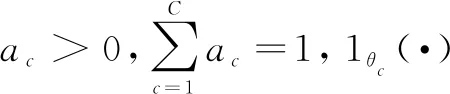
ANM_MM模型中所有的观测数据都是由同一个形式的函数f不同的参数θ生成,因为在每个独立的试验中,由于某些难以控制的外部因素的影响,数据生成过程略有不同。此外这些因素通常被认为是独立于观测变量的。
2.2 HilberSchmidt独立性准则
二元变量的独立性测试方法有很多,文中使用的是HilberSchmidt独立性准则。假设X,Y是两个一维变量,定义一个非线性映射φ(x)∈F,F属于再生核希尔伯特空间(reproducing kernel Hilbert space)且x∈X,再定义一个ψ(y)∈G,G同样属于再生核希尔伯特空间且y∈Y,则相应的核函数分别记为:
k(x,x')=〈φ(x),φ(x')〉,x,x'∈X
(1)
l(y,y')=〈ψ(y),ψ(y')〉,y,y'∈Y
(2)
对于所有的f∈F,g∈G定义:
〈f,Cxyg〉F=Exy([f(x)-Ex(f(x))][g(y)-
Ey(g(y))])
(3)
交叉协方差算子Cxy:G→F且:
Cxy=Exy[(φ(x)-μx)⊗(ψ(y)-μy)]
(4)
其中,μx=Exφ(x),μy=Eyφ(y),⊗为张量积,Cxy可以看作Hilbert-Schmidt算子,然后将Frobenius范数扩展到该算子上,得到Hilbert-Schmidt范数,将该范数平方即可得到Hilbert-Schmidt独立性准则:
(5)
其中,Prxy是X,Y的概率分布。
3 模型可识别性和参数估计
3.1 模型的可识别性
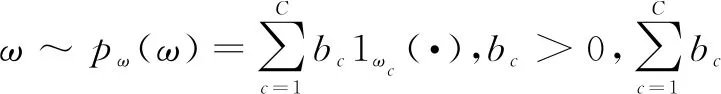
(6)


图2 因果推断示意图
根据定理可以通过研究假设原因与相应函数参数之间的独立性,推断出模型的因果方向,如果它们在因果方向上是独立的,那么它们很可能在反因果方向上是相互依赖的。因此在实际中两变量间的因果推断的方向是变量和中间参数之间独立性更大的方向。
3.2 参数估计
在ANM-MM模型中利用目标函数的对数似然极大化通过梯度下降来寻找潜在的分布参数的表示形式,然而θ不能直接通过极大似然估计进行求解,所以ANM-MM需要添加X和分布参数θ之间的HSIC独立性到损失函数得到:

λlogHSICb(X,Θ)]
(7)
由于在求解分布参数的过程中没有考虑到结果变量对分布参数的影响,文中修改了ANM-MM模型的损失函数(7),另外添加Y和分布参数θ之间的HSIC独立性到损失函数得到:

λlogHSICb(X,Θ)+
α(1-λ)logHSICb(Y,Θ)]
(8)
其中,λ控制原因变量X和分布参数之间的Hilbert-Schmidt独立性,α用来调节结果变量Y和分布参数的Hilbert-Schmidt独立性,当λ增大时即增强X和分布参数的独立性,由于结果变量前又有(1-λ)进行约束,则Y和分布参数独立性势必会减小,因此并未违反因果逻辑性。当α=0时,文中使用的目标函数(8)和ANM-MM的目标函数(7)具有一致性。由于该目标函数包含两个方向上的独立性测试,因此文中算法记作Dual-ANMM,另外当α=1时目标函数改写为:

λlogHSICb(X,Θ)+
(1-λ)logHSICb(Y,Θ)]
(9)
其中,目标函数(8)引入α的目的是控制数据和参数之间HilberSchmidt独立性的强弱。文中在实验中使用神经网络来学习,采取梯度下降法最优化α=1的目标函数(9)得到混合数据的抽象因果分布参数。
4 算法过程
文中使用了三层网络结构来学习混合数据的分布参数,第一层是Normlization layer,该层网络主要将输入数据正则化、规范化;第二层是Full-Connect全连接层,文中采用的是10个神经元;最后一层是激活层,文中使用的是LRelu激活。最后将通过梯度下降法求得目标函数(3)的最小值从而得到混合数据的分布参数。再通过HilberSchmidt独立性测试确定因果方向,如图3所示。
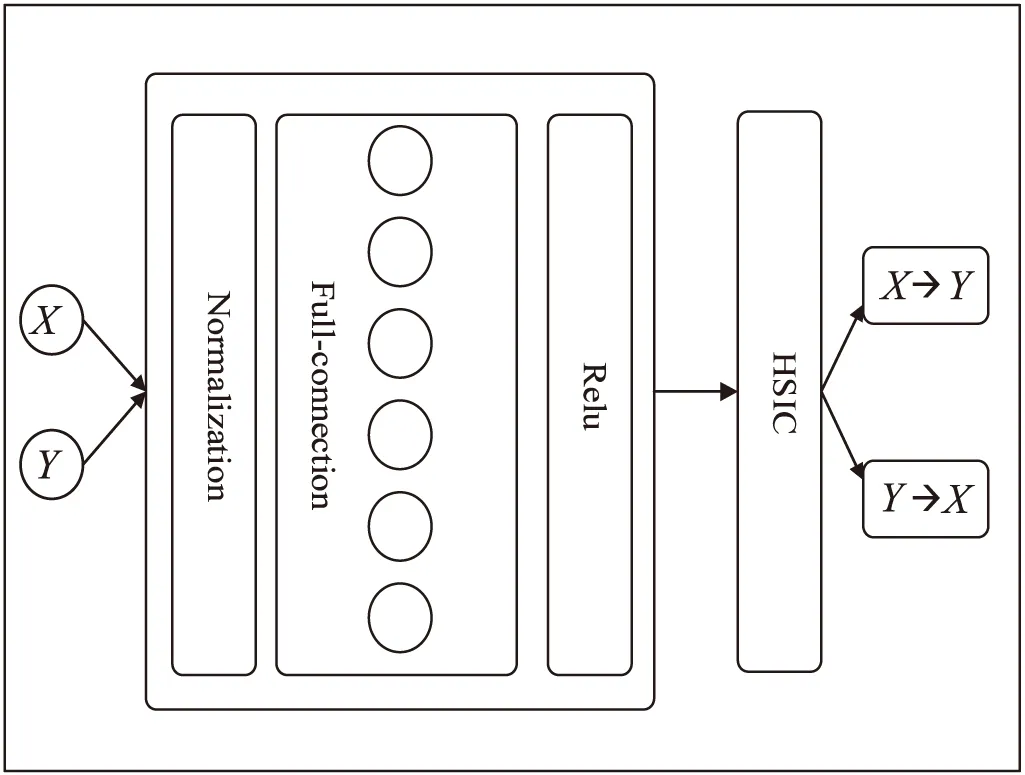
图3 网络架构
当HSIC(X,θ1)>HSIC(Y,θ2)时,X→Y;
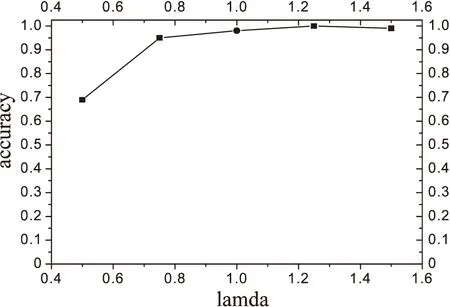
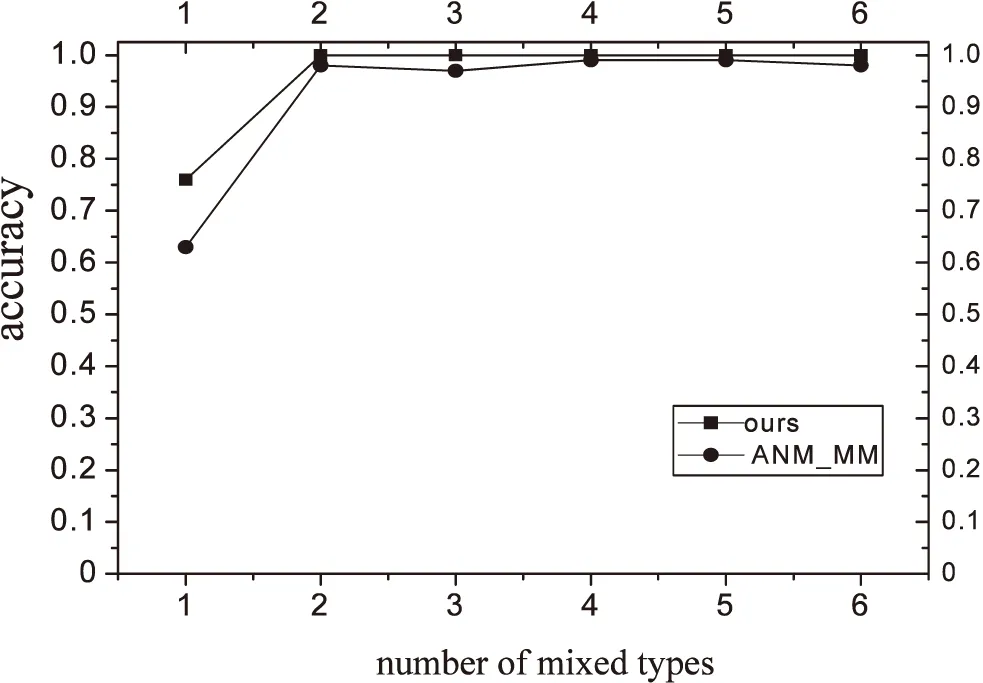
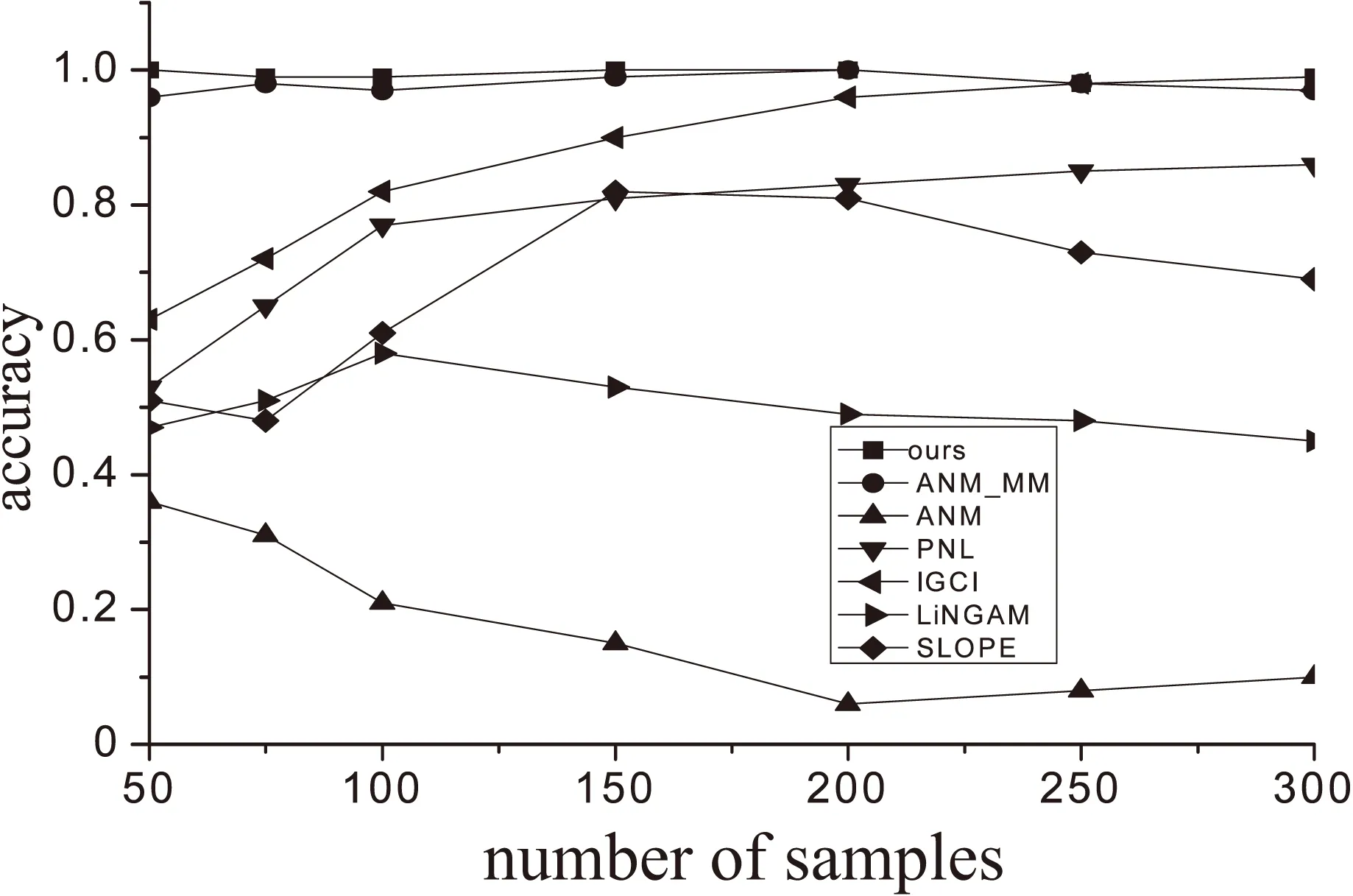
当HSIC(X,θ1) 当HSIC(X,θ1)=HSIC(Y,θ2)时无法识别,第三种情况在实际情况下很少发生。文中使用的HilberSchmidt独立性是Hu Shoubo改进的GPPOM_HSIC独立性方法。 Dual-ANMM算法过程如下: Algorithm Dual-ANMM(A kind of causal discovery by neural network) 输入:D,alpha=1,lamda//其中D是数据,alpha和lamda为超参数 输出:direct//输出方向 1.Standardize observation of eachD; 2.Random initialize weight of NN and other argument 3.Optimize target function by NN inX->Yestimate theta1 4.D1=HSIC(theta1,X) 5.Optimize target function by NN inY->Xestimate theta2 6.D2=HSIC(theta2,X) 7.IfD1 8.ElifD1 9.Else direct =0 10.Return direct LiNGAM模型[10]是一种线性非高斯因果推断模型,LiNGAM模型假设数据由E=βC+N产生,其中β属于实数域,C⊥N并且N是非高斯的。LiNGAM仅适用于非高斯噪声的线性关系,因此如果生成的数据违反了该假设,LiNGAM模型会表现得极差。如果数据之间的关系是线性函数的关系,识别率会提高,而且计算成本相对较低。在实验中,文中使用的LiNGAM是原始版本中基于独立成分分析的算法。 ANM模型[12]是一种加性噪声模型,ANM模型假设E=f(C)+N,这里的f是非线性函数并且C⊥N,该方法能够处理非线性数据。由于现实世界中的数据大多是非线性数据,该方法得到了广泛的应用。ANM算法识别因果关系使用原因和结果之间的不对称来检测,原因和结果之间的不对称是通过原因和残差之间独立的假设实现。因此该方法需要拟合回归函数,并对输入与的选择对性能识别率是至关重要的。在实验中,文中使用了Mooij等人(2016)提出的一种实现,该实现使用高斯过程回归进行预测,并使用熵估计进行输入和残差之间的关系评估。 PNL模型[11]是一种后线性模型,该模型是对ANM模型的一种泛化。PNL模型假设数据的生成机制是由E=g(f(C)+N)表示,其中g是非线性函数,f是线性函数,并且C⊥N。为了推断出因果关系的方向,在两个可能的方向上进行PNL模型测试,并检查输入和扰动之间的独立性。然而这里的扰动不同于回归残差,拟合PNL模型比拟合ANM要困难得多,准确率较高于ANM模型。在实验中,文中使用了基于约束非线性独立分量分析来估计扰动,并使用HilberSchmidt独立性准则进行统计独立测试。 实验在CentOS系统上python3.6环境中进行,分别在模拟数据集和真实数据集上实验,其他对比实验包括LiNGAM,IGCI,PNL,ANM分别按照上面实现方法在matlab2016a中进行。SLOPE实验是R3.5.2中进行。首先比较了λ对实验准确率的影响,在实验中分别取λ为0.5,0.75,1.0,1.25,1.5,其中当λ等于1.0的时候该模型等价于ANM-MM模型使用的损失函数。文中对混合数据类型个数对因果推断的准确率的影响进行了实验,然后是数据量对ANM-MM,ANM,IGCI,PNL,SLOPE,LiNGAM的影响进行了实验,最后在cause-effect pairs真实数据集上评估了算法的因果推理性能。cause-effect pairs具有用于测试因果检测算法的不同数据,数据文件一共包含108个txt文件,每个文件包含两个变量,一个是原因,另一个是效果。对于每个数据文件,都有一个描述性文件,可以在其中找到真实的因果关系以及数据来源描述,实验中108组数据中有9组被排除在外,因为它们要么由多变量数据组成,要么由分类数据组成(对47、52、53、54,55、70、71、101和105)。每对实验重复100次独立实验,记录不同方法的正确推理率。然后计算同一数据集对的平均百分比作为对应数据集的精度,实验结果如下。 如图4所示,实验测试了λ对实验准确率的影响,其中当λ等于1.0时表示ANM_MM模型对应的目标函数,实验表明α=1.0时,λ=1.25时结果会达到最好。 如图5所示,实验对比了混合数据类型个数对两种算法的影响。可以看出文中提出的算法是优于ANM-MM模型的,在实验中,当只有一种因果机制的时候ANM-MM模型的准确率低于65%,这是在100次重复实验中得到的结果,而文中提出的Dual-AMMM在参数α=1.0,λ=1.25时准确率能达到77%,即当数据并不是由多种因果机制生成,ANM-MM识别率低于Dual-AMMM。在多于一种混合类型的数据时,Dual-AMMM算法和ANM-MM模型结果不相上下。 图4 λ对实验准确率的影响 图5 混合数据类型个数对准确率的影响 该实验对比了几种不同的传统的因果推断算法和ANM-MM模型在不同数据量下的模拟数据的准确率,如图6所示。实验结果表明,在不同的数据量下,该算法在稳定性上优于传统的方法,其中ICGI在数据量增加时结果逼近文中提出的Dual-AMMM算法以及ANM-MM模型,由上图可以看出Dual-AMMM和ANM-MM原始算法和在稳定性和准确率上都优于其它方法。 图6 数据量对模型的影响 该实验在真实因果数据集cause-effect pairs上进行,结果如图7所示,柱状图的高度表示实验100次的平均准确率,其中Y的误差取上下界误差的最大。结果表明文中提出的Dual-AMMM算法优于其他传统的方法,平均准确率最高约85%左右,ANM-MM算法在82%左右。PNL也表现很好,其次是IGCI算法,但是IGCI和SLOPE的误差范围较大。 图7 在真实数据集上的对比 在ANM-MM的假设基础上提出了一种基于神经网络的因果推断方法。该方法使用梯度下降法最优化损失函数得到混合数据的抽象因果分布参数,然后将分布参数看作是原因变量和结果变量之间的隐变量,通过比较原因变量和分布参数之间的HilberSchmidt独立性来确定二元变量的因果方向。由于改进的ANM-MM求解分布参数的过程中没有考虑到结果变量对分布参数的影响,在实验上也表现出较其他传统的方法具有较好的稳定性和准确率。但是现阶段的研究主要是在二元变量之间的因果方向推断,因此将该方法推广到多元变量之间的因果图的识别是下一阶段的主要内容。5 传统因果推断方法对比
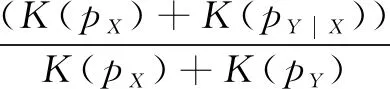
6 实验过程
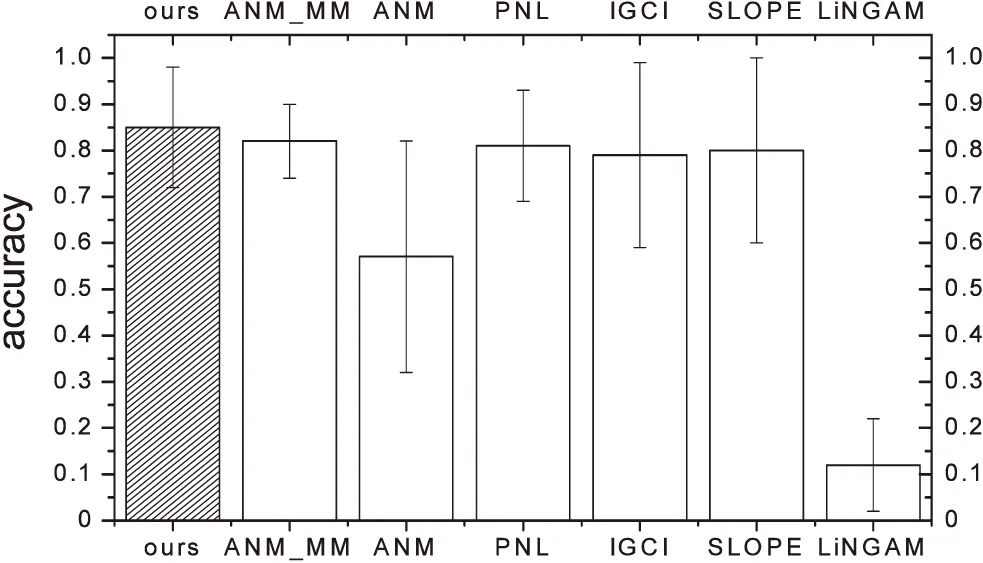
7 结束语
