基于随机久期缺口控制的全资产负债优化模型
2020-05-21迟国泰张志鹏
迟国泰,张志鹏,刘 艳
基于随机久期缺口控制的全资产负债优化模型
迟国泰,张志鹏,刘 艳
(大连理工大学 管理与经济学部,辽宁 大连 116024)
资产负债管理是银行等金融机构在负债结构和总量一定的前提下,通过对资产进行优化配置,达到资产流动性、盈利性和安全性“三性”之间的平衡。本文基于CIR动态利率期限结构求解随机久期,对包括增量和存量在内的全部资产负债组合的久期缺口进行预留和约束,构建资产负债优化模型控制利率风险。本文的创新与特色有三:一是以控制CIR利率期限结构的随机久期缺口为约束条件建立非线性规划模型、对资产配置进行利率风险免疫,反映了利率随时间的动态变化,突破了Macaulay久期、FW久期等现有研究的利率随时间的变化是固定不变或平行移动的限定条件,使资产配置的利率风险免疫更加符合现实情况。二是建立了包括增量资产负债与存量资产负债的全资产负债优化配置模型,改变了现有资产负债模型大多只考虑增量资产负债、而忽略存量资产负债的弊端。三是以市场利率朝着最不利方向变动时、预留缺口损失后的资本充足率仍满足监管要求为约束条件,保证了在利率不利变动情况下损失仍在可控范围内,在利率有利变动时银行净值增加。
银行资产负债管理;利率风险控制;随机久期;CIR模型;全部资产负债组合
0 引言
资产负债管理(Asset Liability Management, ALM)是银行等金融机构在负债结构和总量一定的前提下,为了实现安全性、流动性和盈利性的目标,而对资产进行优化配置的过程。
由于资产等于负债加上所有者权益,所以当利率变化时,银行的资产和负债的价值都会相应地发生变化,而两者的变化幅度不可能总是一致,所以所有者权益价值不可避免的会发生变化。因此利率风险是资产负债管理中必须控制的风险之一。
基于利率风险控制的资产负债管理优化模型可以分为两类:
第一类是基于资金缺口管理的资产负债组合优化模型。资金缺口管理是对某一期间内将要到期的利率敏感性资产与利率敏感性负债间的账面资金缺口进行测算,以消除利率波动对银行净值的影响[1,2]。但此模型忽略了货币的时间价值,无法真实反映各期现金流受利率的影响[3]。
第二类是基于久期控制的资产负债组合优化模型,具体包括:
(1)基于Macaulay久期或F-W久期的资产负债管理优化模型。Macaulay[4]最早提出久期概念,即各期现金流的加权平均时间。基于Macaulay久期进行资产负债管理利率风险控制的研究较多[5,6],但由于Macaulay久期依赖于利率期限结构平坦、且收益率曲线平行移动等前提,故该类模型在免疫利率非平行移动时存在缺陷。Fisher和Weil考虑了未来利率的变化、得到基于F-W久期的利率风险免疫方法[7]。现有研究基于F-W久期构建了资产负债优化模型[8-10]。虽然F-W久期允许收益率曲线为任意形状、但其仍隐含利率期限结构平行移动的假设,故对利率风险的控制效果并不理想[11]。
(2)基于多元久期免疫的资产负债管理优化模型。多元久期包括方向久期等离散多元久期,也包括M2等多元参数久期[12]。代表性的研究有:刘艳萍等通过方向久期来反映及其收益率的波动对现金流的影响,建立了以方向久期的免疫条件为约束,以组合收益最大为目标函数的资产负债组合优化模型[13]。吴灏文等基于方向久期及方向凸度来建立控制利率风险的免疫条件,构建了银行资产负债组合优化模型[14]。杨婉茜通过Nelson-Siegel模型将利率变化分解为水平、斜率和曲率三方面,以久期向量零缺口为约束条件建立模型[3]。信怀义通过M向量多维久期建立利率风险免疫模型[15]。多元久期方法的计算过程复杂、通常通过令久期缺口为0的方式控制利率风险,无法在利率发生有利变动时增加银行净值。
(3)基于随机久期免疫的资产负债管理优化模型。随机久期类资产负债优化模型通过利率的随机过程描述收益率曲线的非平行变动、进而对资产负债管理中的利率风险进行控制。代表性的研究有:基于Vasicek动态利率期限结构及久期表达式[16]构建的随机久期免疫的资产负债模型[17],以及基于Cox、Ingersoll和Ross提出的CIR随机久期[18]构建的动态利率风险免疫模型[19]。这类随机久期的资产负债配置研究较少,在配置中考虑包括已配置的存量和未配置的增量的文献更少。
综上所述,现有研究在利率风险控制方面已经取得了较大的进展,但仍存在以下问题:
(1)现有研究在构造资产负债管理模型时,大多只针对还未进行配置的增量资产和负债,没有考虑已经配置过的存量资产负债对配置结果的影响[3,5,6,9-15]。只着眼于“增量”资产负债的风险控制,并不能保证包括“增量”和“存量”在内的全部资产负债组合的风险得到控制。事实上,由于银行即将配置的增量资产规模较小、存量资产规模较大,一旦利率出现不利波动、存量资产负债造成的损失将远大于增量资产造成的损失。银行家们真正关注的是存量与增量在内的全部资产负债组合利率风险。控制“存量”与“增量”在内的全部资产负债组合的利率风险极为必要。
(2)现有研究[3,5,6,8-10]在衡量利率风险的过程中,大多采用的是Macaulay久期或静态久期,并未考虑利率的动态变化对久期的影响,这样的利率风险测量相对来说是不准确的。
(3)现有研究大多令久期缺口最小为目标函数或者久期缺口为0作为约束条件[9,10,19],这样虽然能够使银行在利率变化过程中规避风险,但也使银行失去在利率变化过程中增加所有者权益的机会。
本文基于CIR动态利率期限结构模型,得出考虑利率动态变化的随机久期。通过控制包括增量和存量在内的全部资产负债组合的利率风险,构造全资产负债模型。通过预留久期缺口而非令缺口为0,当利率出现有利变动时增加银行所有者权益。基于随机久期缺口控制的全资产负债优化模型原理如图1所示。

图1 基于随机久期缺口控制的资产负债优化原理
Figure 1 Principle of asset liability optimization based on stochastic duration gap control
1 随机久期缺口控制的全资产负债优化原理
1.1 CIR利率模型和随机久期
银行的实际业务中,贷款利率并非固定不变、而是具有波动性、随机性等特征[20],传统久期模型不能准确地识别实际利率的随机变化。随机久期基于动态利率期限结构提出,可以更好地描述收益率曲线的非平行移动等动态变化[17]。本文正是基于CIR动态利率模型和对应的随机久期,通过建立随机久期缺口约束利率风险,对资产进行优化配置。
Cox,Ingersoll和Ross在连续时间框架下,采用一般均衡方法构造了动态利率期限结构模型[18]:


根据式(1)所示的CIR动态利率期限结构,可得基于CIR利率期限结构的随机久期为[21]:
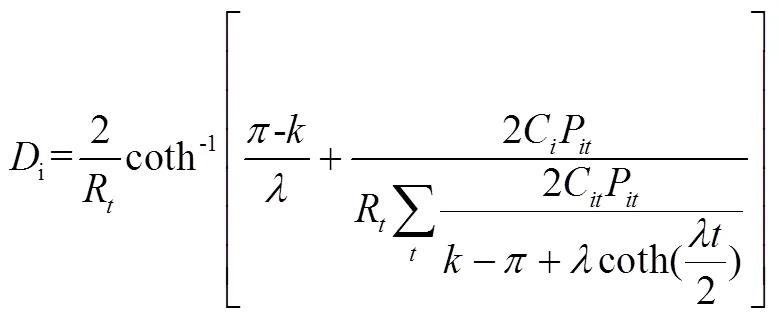
其中:D-第项资产或负债的久期;R-即期利率;coth-反双曲余切函数;-流动性溢价(并非圆周率,故值不为3.1415);-利率的均值回复速度;-参数变量;C-第项资产或负债到期时的现金流;P-第项资产或负债在第期的到期价值,需要通过市场利率R进行折现;C-第项资产或负债在第期的现金流,当资产或负债尚未到期时、C等于到期前第期现金流C,当资产或负债到期时,现金流C等于到期时现金流C。
应该指出,本文的式(2)与现有研究[21]的差别是:当计算存量的资产或负债时,这里的期限为剩余期限。例如,对于一笔已发放3个月的1年期贷款,则在代入式(2)的随机久期计算时,代入9、而非12,即将该笔贷款视为期限为9个月的新增贷款。这才会为计算存量和增量叠加后的资产负债组合风险打下基础,其好处下文再述。
式(2)的好处在于基于CIR动态利率期限结构,将利率的随机变化考虑在内,改变了Macaulay久期、F-W久期等不能识别利率随机变化的弊端。通过建立基于随机久期缺口控制的利率风险免疫条件,在控制利率风险的情况下最优配置资产。确保在利率发生变化时,银行股东的所有者权益不受损失。
1.2 基于存量与增量的随机久期缺口预留原理
大多数研究采用零缺口免疫方式控制利率风险[9,10,19]。但是,由于资产和负债每时每刻的变动,实践中总会或大或小地存在缺口,“零缺口”目标并不能达到[22]。此外,“零缺口”无法使银行在利率发生有利变动时增加净值。
本文在随机久期基础上,通过考虑存量与增量在内的全部资产负债久期并预留久期缺口,在控制风险的同时把握市场机会。
一般的久期缺口可表示为[6]:

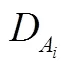
在本研究中,通过考虑存量与增量在内的全部资产或负债的随机久期,得到反映增量与存量资产负债的随机久期缺口[22]:
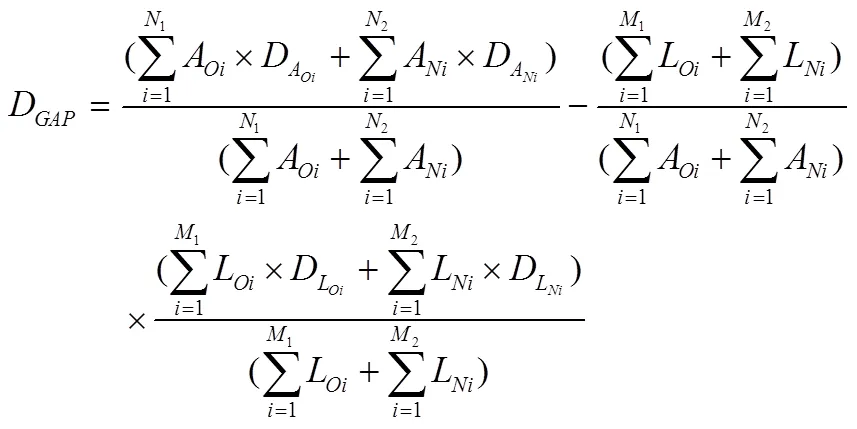
式(4)的经济学含义:式(4)右边第一项为增量和存量资产的随机久期,第二项为负债总额与资产总额的比值,第三项为增量与存量负债的随机久期。故式(4)是考虑了增量和存量在内的全部资产负债组合的随机久期缺口。
式(4)与式(3)的区别:现有研究通过式(3)计算久期缺口时、只考虑了“增量”的资产负债的风险控制。事实上,由于银行存量资产负债规模远大于增量资产负债规模,一旦利率出现不利波动、存量资产负债造成的损失亦将远大于增量资产造成的损失,故需要同时控制“存量”与“增量”资产负债组合的利率风险。本研究通过式(4)对包括“存量”和“增量”在内的全部资产负债的利率风险进行控制。
本研究的式(4)的表现形式与现有研究的缺口表达式相同,但内容或参数不同,其主要区别至少有两点:

二是本研究式(4)的久期,也并不完全是式(2)的CIR随机久期中的参数:形同式(2)的久期[21]中的时间参数是资产或负债的期限,也就是名义期限,因为随机久期是用来研究新增头寸的资产配置[21]。本研究的式(2)中的时间参数用的是“剩余期限”,因为只有“剩余期限”这个参数才能反映存量和增量资产负债的全部组合风险。不言而喻,忽略巨额的存量资产来仅仅研究为数相对很少的增量资产组合风险,并没有实际意义。
1.3 基于随机久期缺口的利率风险控制原理
1.3.1 随机久期缺口的方向控制原理
若预测未来利率会上升,则预留负缺口,以保证银行所有者权益增加[23],即:

若预测未来利率会下降,则预留正缺口,仅将式(5)不等式的符合的小于号“<”,替换为大于号“>”。其他不变。
式(5)的特点在于通过预留久期缺口,当利率有利变动时,银行可以增加所有者权益。改变了现有研究大多采用久期零缺口模型[9,10,19]、当利率有利变动时银行所有者权益无法增加的弊端。
1.3.2 随机久期缺口的大小控制原理
正确的预留缺口可以帮助银行在利率变化的过程中获得利润,但银行对利率变化趋势的预测不能保证总是正确。当预测错误时,银行就可能会遭受损失,因此需要将损失控制在银行可接受的范围内。
当利率发生变动时,银行的所有者权益变化可以表示为[24]:
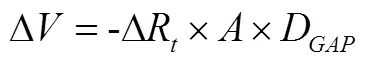


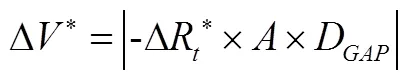
利用资本充足率对预留缺口进行约束,使利率发生不利变化时,银行的资本充足率也可以满足商业银行法和监管当局的要求。
则资本充足率的约束条件可以表示为[24]:
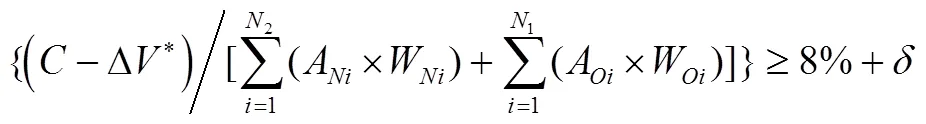

2 CIR模型和随机久期各参数的确定
2.1 CIR模型的参数估计
通过离散模型方法估计CIR模型参数,即[25]:


式(10)的经济学含义:揭示了第t+1时的利率R+1与第时的利率R之间的关系,将连续的市场利率离散化。

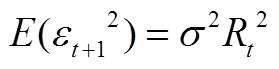
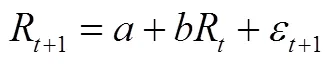





应该指出,若用来拟合CIR的利率数据为单利,则需要转换为复利形式,即[28]:

2.2 市场利率的拟合
根据式(2)可知,第项资产或负债在第期的到期价值P,需要通过市场利率R进行折现。因此需要对市场利率进行拟合。
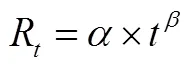
应该指出,上文2.1中的式(10)已经拟合了利率R的表达式,这里的式(19)还在对R进行再次拟合,其原因在于式(10)和式(19)的拟合用途不同。
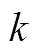
而式(19)则是描述利率R与期限的函数关系,目的在于通过期限确定市场利率,其用途在于对资产或负债的到期价值P进行折现。
2.3 随机久期参数的确定
CIR模型的参数一旦估计得到,可以得到CIR随机久期。为阅读方便,在此再次列出式(2),并重新编号为式(20),各字母含义同式(2)。
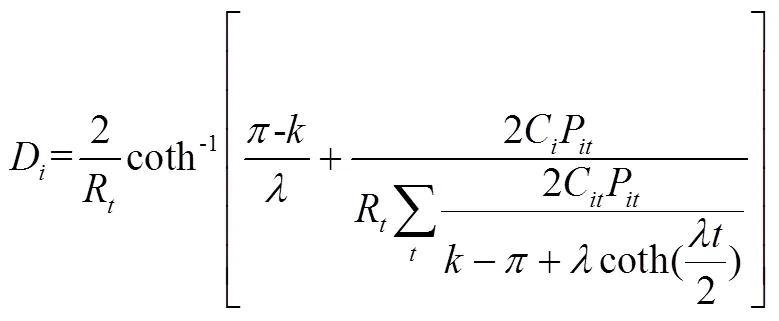
如前所述,D-第项资产或负债的久期;R-即期利率;coth-反双曲余切函数;-流动性溢价(并非圆周率,故值不为3.1415);-利率的均值回复速度;-参数变量;C-第项资产或负债到期时的现金流;P-第项资产或负债在第期的到期价值;C-第项资产或负债在第期的现金流,当资产或负债尚未到期时、C等于到期前第期现金流C,当资产或负债到期时,现金流C等于到期时现金流C。
其中[21]:
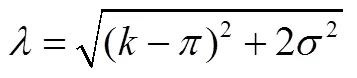
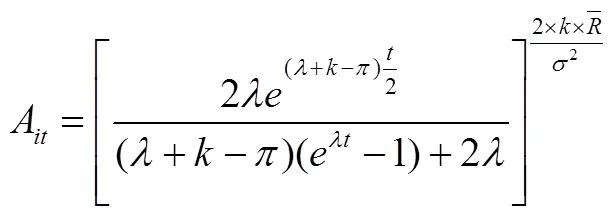




此外,在通过式(20)求解随机久期D时,需要用到第项资产或负债到期时的现金流C、第项资产或负债在第期的现金流C。
设:C-第项资产或负债到期时的现金流;L-第项负债的账面价值;R-第项资产或负债的票面利率;C-第项资产或负债在到期前第期的现金流;A-第项资产的账面价值。
对于包括存量与增量在内的负债,到期时的现金流计算公式为[17]:
C=L×R×t+L(25)
对于包括存量与增量在内的资产,到期前每期的现金流计算公式为[17]:
C=A×R (26)
对于包括存量与增量在内的资产,资产到期时的现金流计算公式为[17]:
C=A+C(27)
3 银行全资产负债优化模型的构建
3.1 目标函数的构建
银行追求的是全部资产的月利息收入最大,但是由于存量资产各项目的数额和利息收入已经为确定值,故只要银行增量资产的月利息收入最大,就能保证银行全部资产的月利息收入最大。
因此以增量资产利息收入最大为目标函数:

其中,2为新增资产的总项目数,X为第项新增资产的账面价值,R为第项新增资产的利率。
3.2 约束条件的构建
3.2.1 预留缺口约束条件
根据上文1.3,随机久期缺口的方向可由式(5)控制,随机久期缺口的大小可由式(9)控制。因此,分别以式(5)和式(9),约束预留缺口。
为方便阅读,再次给出式(5)并编号为式(29):

在此再次给出式(9)并重新编号为式(30),即:
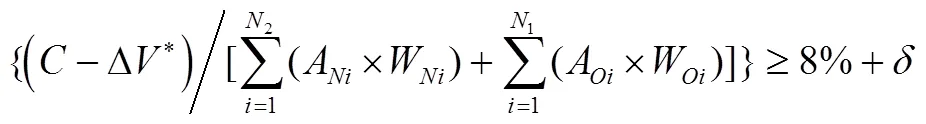
式(29)-(30)与现有研究的区别至少有三:

二是久期不一样。现有研究中久期[21]中时间参数是资产或负债的期限,也就是名义期限,因为CIR模型是用来研究新增头寸的资产配置[21]。本研究的久期中时间参数用的是“剩余期限”,因为只有“剩余期限”这个参数才能反映存量和增量资产负债的全部组合风险。不言而喻,忽略巨额存量资产、而仅考虑为数相对很少的增量资产风险并无意义。
三是现有研究采用的是零缺口[9,10,19]、而本研究预留了久期缺口。一方面由于在实践中很难保持零缺口[22],另一方面零缺口也不能使银行享受利率变动带来的收益。本研究的式(29)-(30)不仅能根据对利率的判断、在利率有利变动时增加银行净值,又可在利率发生不利变动时控制风险。事实上,利率的中长期变化是可以预测的。
3.2.2 其他约束条件
根据银行资产和负债的数量结构匹配原理[22],辅以法律法规和银行经营管理的要求,得到(31)-(38)的约束条件。
(1)资产规模约束:即新增资产的总额应该等于新增负债的总额[24]。

其中,A-增量资产总额;2-增量资产的总项目数;X-需要配置的第项增量资产;L-增量负债总额。

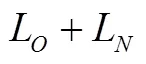
其中,A1-存量库存现金;1-需要配置的增量库存现金;L-存量负债总额;L-增量负债总额。
(3)非负性约束,即将配置的各项增量资产均应大于等于0[24]。
X≥0(=1,2,) (33)
其中,X-第项需要配置的增量资产。
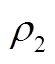

其中,1-增量资产中的短期资产项目数;X-需要配置的第项增量资产项目;2-存量资产中的短期资产项目数;A-第项存量资产;3-存量负债中的短期负债项目数;L-第项存量负债;4-增量负债中的短期负债项目数;L-第项增量负债。
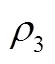
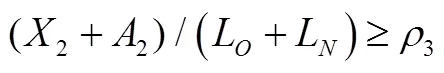
其中,2-增量存款准备金;2-存量存款准备金;L-存量负债总额;L-增量负债总额。

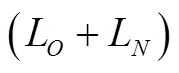
其中,A1-存量库存现金;A3-存量备付金;1-增量库存现金;3-增量备付金;L-存量负债总额;L-增量负债总额。
(7)中长期贷款结构约束,根据银行对贷款期限的偏好确定。例如,5年期贷款的数额应小于等于3年期贷款的数额;8年期贷款的数额应小于等于5年期贷款的数额[24]。
5≤3(37)
8≤5(38)
其中:5是5年期贷款;3是3年期贷款;8是8年期贷款。
综上,以式(28)为目标函数,以式(29)和式(30)的预留缺口上下界为约束条件,辅以约束条件(31)-(38),建立银行资产负债优化模型。
4 银行全资产负债优化模型的构建
4.1 CIR模型参数的确定
4.1.1 样本的选取
选取上海银行间同业拆放利率(SHIBOR)数据作为CIR模型参数估计的数据来源。由于SHIBOR隔夜利率及一月利率的短期变化趋势与其它利率高度相关,并且以其为标准的衍生品交易量大,非常有代表性[28]。但是考虑到时间跨度及数据量,最终选用2012年到2016年SHIBOR隔夜利率作为估计数据,数据来源为锐思数据库。
表1前3列的信息来源于锐思数据库。
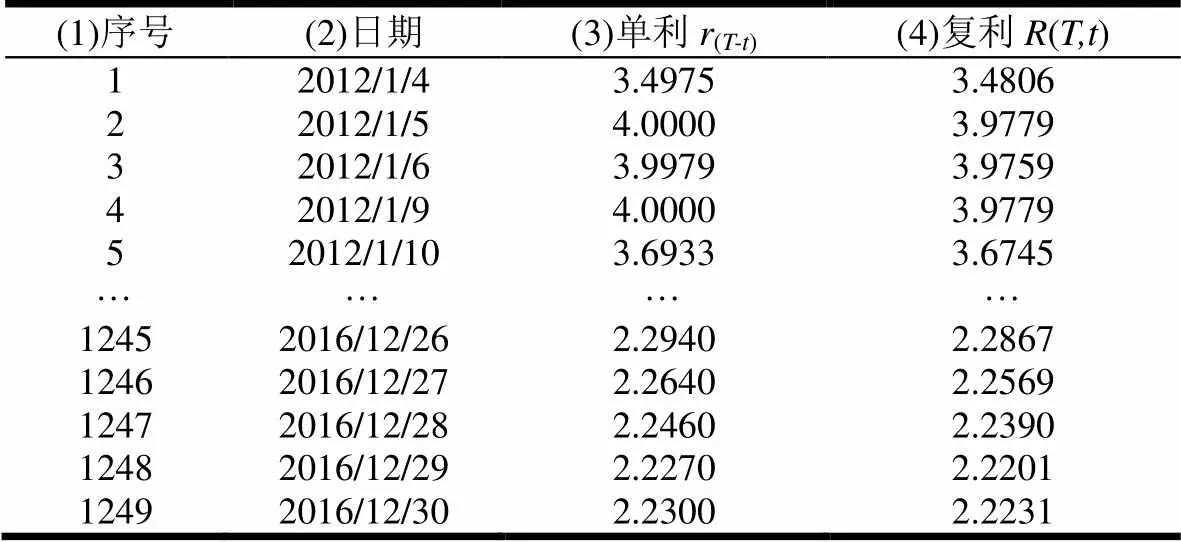
表1 SHIBOR隔夜利率及连续复利数据
由于查询到的SHIBOR利率为单利,故需要根据式(18)转换为复利形式。
将表1第3列SHIBOR隔夜利率单利数据代入公式(18),得到转换后的连续复利,列入表1第4列。


表2 SHIBOR利率拟合需要的数据
4.1.2 CIR模型的参数估计
表3第4列第1-2行是参数、估计值对应的检验显著性水平,由于sig均为0.00<0.01[29],故参数均通过了检验。

列入表3第3列第5-6行。

列入表3第3列第7行。

表3 CIR模型参数估计结果
4.2 市场利率的拟合
选用2017年5月3日的国债即期利率数据,对市场利率进行拟合。表4中的数据来源为Wind数据库。
以表4第3列的即期利率R为因变量,表4第2列的期限为自变量,拟合式(19)中的参数及。参数估计的结果如表5所示。

表4 国债即期利率数据
表5第1行第3列拟合优度R=0.908>0.5,所以拟合效果较好[30]。表5第2行是检验显著性水平,0.00<0.01,说明参数估计显著[29]。表5第3-4行是估计得到的参数及值,2.778,=0.055。

表5 模型汇总和参数估计值
将表5第3-4行的=2.778,=0.055,代入公式(19),得到:
R2.778×0.055(39)
式(39)即为市场利率R与期限的表达式。
4.3 随机久期参数的确定
对流动性溢价,本文也像现有研究[19]那样不考虑流动性溢价的影响,即=0。
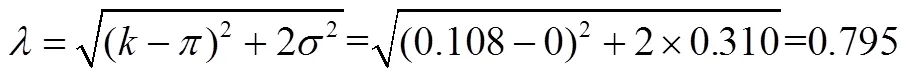
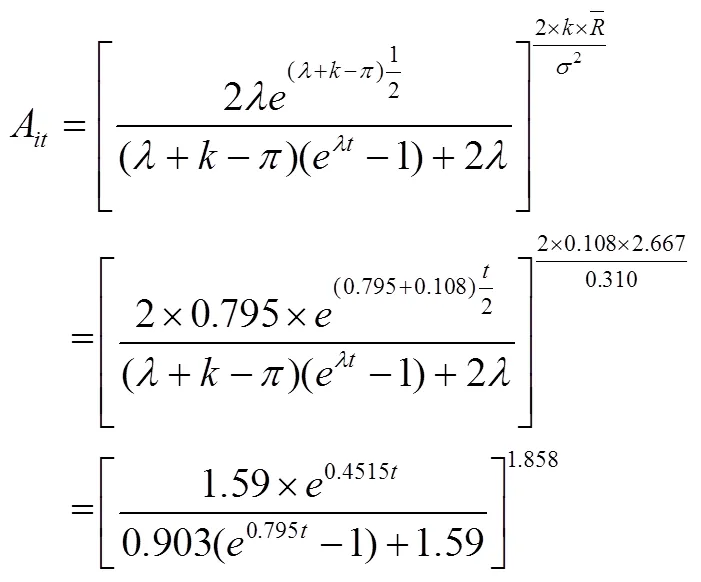
将表3中第6行=0.108,以及λ=0.795及=0,代入公式(23),得到参数B的表达式:

将式(40)计算得到的表达式A表达式,式(41)计算得到的B表达式以及λ=0.795代入式(24),得到市场价值P:

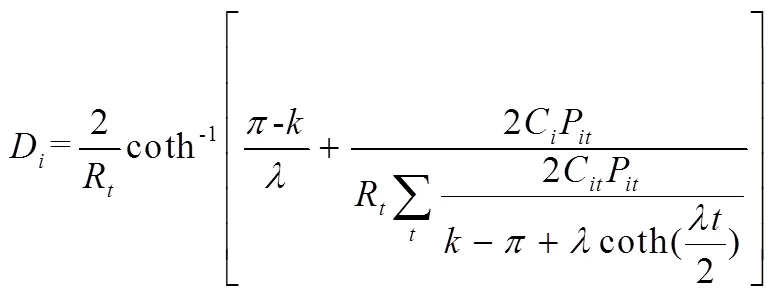
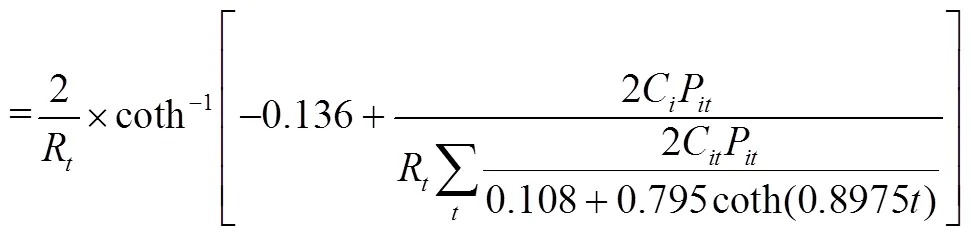
应该指出,式(43)是一个通式,可以计算存量资产、存量负债、增量资产以及增量负债等的久期,详见下文4.4.2。
4.4 银行数据及其有关参数的确定
4.4.1基本数据和现金流的计算
(1)存量负债数据及有关参数的计算
表6前6列来源于某商业银行。
表6第7列是表6第6列的代入式(39),计算得到的利率R列入表6第7列。
表6第8列亦来源于商业银行。
表6第9列是到期前每期的现金流C。因为表6第1-8行的各项存款均为到期一次还本付息,所以到期前每期的现金流C均为0。
表6第10列是到期时的现金流C,是将表6第3列的账面价值L,第6列的剩余期限,第8列的月利率R,代入式(25)中计算得到。
注意到上文的式(42)最后一个等号后的表达式,只与有关,因此、将表6第6列的剩余期限,代入式(42),计算得到P的值列入表6第11列。
(2)存量资产数据及其计算
表7前6列来源于商业银行。
表7第7列是市场利率R,将表7第6列剩余期限的值代入式(39),计算得到的利率R列入表7第7列。
表7第8列亦来源于某商业银行。
表7第9列是到期前每期的现金流C。由于贷款为每月付息一次,故将表7第3列的账面价值A,第8列的月利率R,代入式(26)计算得到。
表7第10列是到期时的现金流C,是将表7第3列的账面价值A,第9列的到期前每期的现金流C,代入式(27)计算得到。
表7第11列是到期价值P,是将表7第6列的剩余期限,代入式(42),计算得到P的值列入表7第11列。
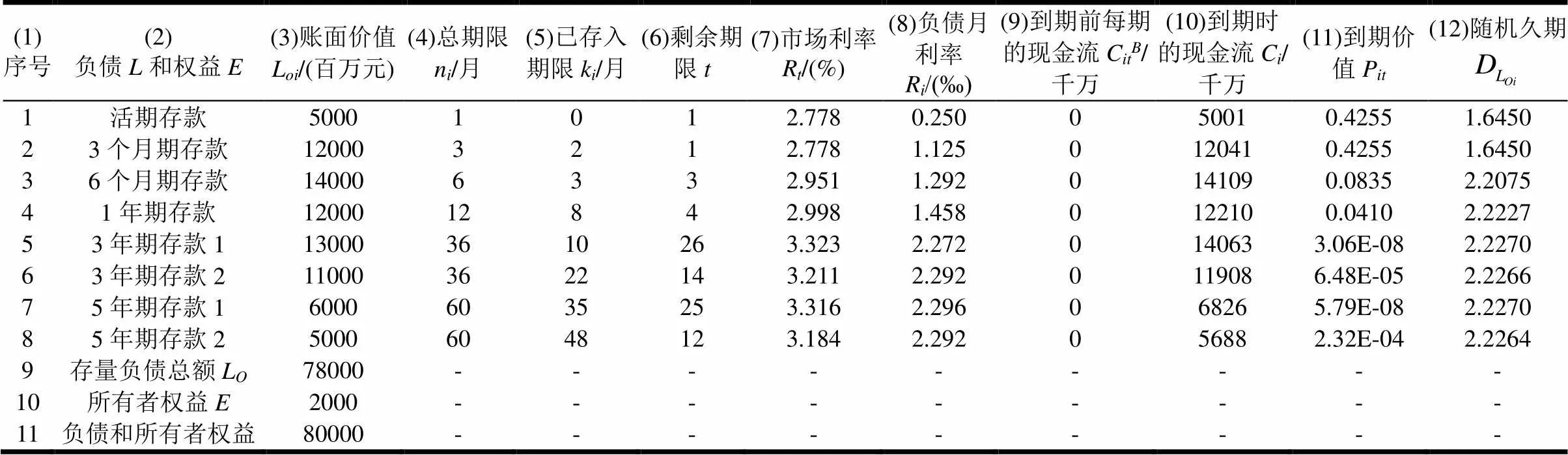
表6 存量负债与所有者权益数据信息

表7 存量资产数据信息
(3)新增负债数据及其计算
表8前5列来源于商业银行。
表8第6列是市场利率R,是将表8第4列期限的值代入式(39),计算结果列入表8第6列。
表8第7列前6行是到期前的现金流C,由于存款为到期一次还本付息,所以到期前的现金流C为0。
表8第8列是到期时的现金流C。将表8第3列的账面价值L,第4列的期限,第5列的月利率R,代入式(25)中计算得到。
表8第9列是到期价值P,将表8第4列的期限代入式(42),得到P的值列入表8第9列。
(4)新增资产数据及其计算
表9前5列来源于商业银行。
表9第6列为市场利率R,是将表9第4列期限的值代入式(39),计算结果如表9第6列。
表9第7列为到期前每期的现金流C,是将表9第3列的账面价值A、第5列的月利率R代入式(26)计算得到。
表9第8列为到期时的现金流C,是将表9第3列的账面价值A、第7列到期前每期的现金流C代入式(27)计算得到。
表9第9列是到期价值P,将表9第4列的期限,代入式(42),计算得到P的值列入表9第9列。
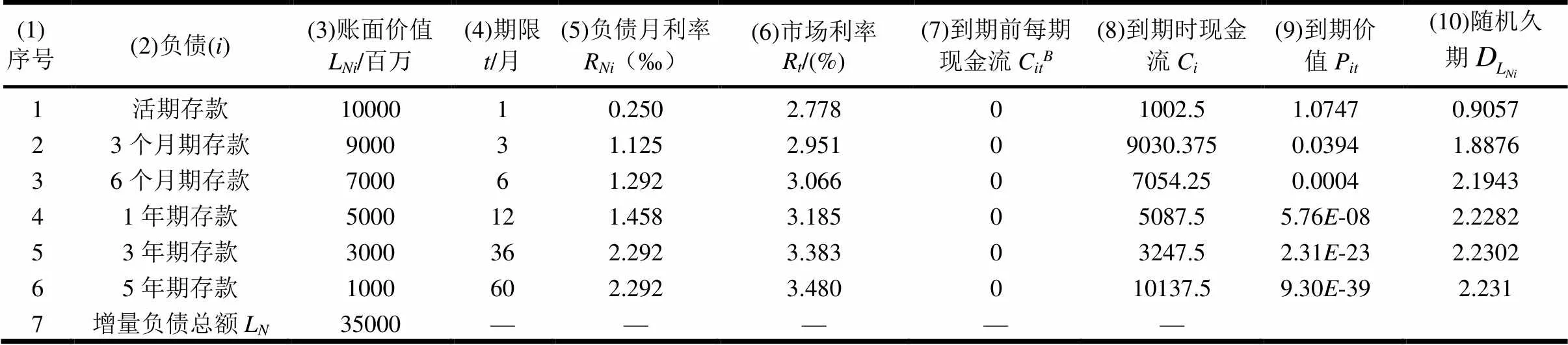
表8 增量负债数据表

表9 增量资产数据表
4.4.2各资产负债的久期计算
(1)存量负债的随机久期计算
由于表6是存量负债及所有者权益数据表,故存量负债的随机久期应通过表6计算。
第1个参数是市场利率R,来源于表6第7列。第2个参数是期限,来源于表6第6列。第3个参数是到期时现金流C,来源于表6第10列。第4个参数是到期价值P,来源于表6第11列。第5个参数是每期现金流C,包括:表6第9列的到期前每期现金流C,以及表6第10列的到期时的现金流C。
(2)存量资产的随机久期计算
由于表7是存量资产数据表,故存量资产的随机久期应通过表7计算。
第1个参数是市场利率R,来源于表7第7列。第2个参数是期限,来源于表7第6列。第3个参数是到期时现金流C,来源于表7第10列。第4个参数是到期价值P,来源于表7第11列。第5个参数是到期前每期现金流C,包括:表7第9列的到期前每期现金流C,以及表7第10列的到期时的现金流C。。
(3)增量负债的随机久期计算
由于表8是增量负债数据表,故增量负债的随机久期应通过表8计算。
第1个参数是市场利率R,来源于表8第6列。第2个参数是期限,来源于表8第4列。第3个参数是到期时现金流C,来源于表8第8列。第4个参数是到期价值P,来源于表8第9列。第5个参数是到期前每期现金流C,包括:表8第7列的到期前每期现金流C,以及表8第8列的到期时的现金流C。。
(4)增量资产的随机久期计算
由于表9是增量资产数据表,故增量资产的随机久期应通过表9计算。
第1个参数是市场利率R,来源于表9第6列前6行。第2个参数是期限,来源于表9第4列。第3个参数是到期时现金流C,来源于表9第8列。第4个参数是到期价值P,来源于表9第9列。第5个参数是到期前每期现金流C,包括:表9第7列的到期前每期现金流C,以及表9第8列的到期时的现金流C。
4.5 银行资产负债优化模型的建立
4.5.1 目标函数的构建
由表9第2列可知资产项目数2=8。将2=8、及表9第5列的月利率R代入式(28),得到:

4.5.2 基于预留缺口的约束条件
本文中预测利率将上升,故预留负缺口[23]。需要通过式(29)并且不等号取小于号“<”,建立负缺口约束。
式(29)共涉及12个参数,其中:
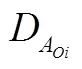
将上述参数代入式(29)并化简,得到预留负缺口约束为:

4.5.3 基于资本充足率的约束条件
本文假定银行董事会决定的资本充足率为11%,银行资本为6900百万。
先假定式(7)中的为2年[24],再根据最终的计算结果判定的取值是否合理。
式(8)涉及3个参数,其中:
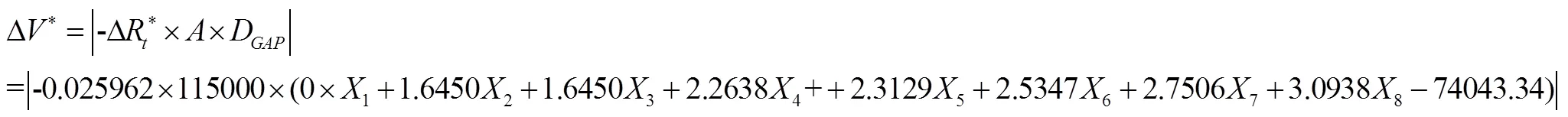
式(30)共涉及9个参数,其中:

将上述9个参数代入式(30),即:
[6900-0.025962×115000×|(0×1+1.64502+1.64503+2.26384+2.31295+2.53476+2.75067+3.09388)-74307.34|]/(0×600+0×13100+0×14500+6000+10000+11800+13000+2000+7000+2000+0×10×20×345678)≥11%
化简得:
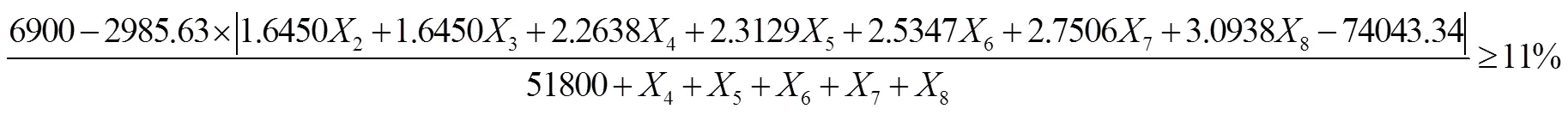
4.5.4 基于流动性风险的约束条件
(1)资产规模对称约束
将表8第3列第7行增量负债总额L=35000、增量资产的项目数2=8、表9第3列增量资产的账面价值X代入式(31),计算得到约束条件如下:
12345678=35000 (48)
(2)库存现金流动性比例约束
库存现金流动性比例约束如式(32),式(32)共有5个参数。其中:
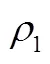
将上述5个参数代入式(32),即:
600+1≥(78000+35000)×0.6%
化简得:
1≥78 (49)
(3)非负性约束:
X≥0 (=1,2,…) (50)
(4)资产流动性比例约束
资产流动性比例约束如式(34),式(34)共有9个参数。其中:

将上述9个参数代入式(34),即:
12345+600+13100+14500+6000+10000≥(5000+12000+14000+12000+10000+9000 +7000+5000)×25%
化简得:
1234544200≥18500 (51)
(5)法定存款准备金约束
法定存款准备金约束如式(35),式(35)共有5个参数。其中:

将上述5个参数代入式(35),即:
2+13100≥(78000+35000)×16.5%
化简得:
2≥5545 (52)
(6)备付金比例约束:
备付金比例约束如式(36),式(36)共有7个参数。其中:
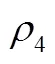
将上述7个参数代入式(36),即:
(600+14500+13)≥ (78000+35000)×5%
化简得:
13+15100≥5650 (53)
(7)中长期存贷款结构约束:
5年期贷款5包括:表7第3列的8-9行的5年期贷款额A8=2000、A9=7000,表9第7行第3列的新增5年期贷款额7。即:5=2000+7000+7。
3年期贷款3包括:表7第3列的6-7行的3年期贷款额A6=11800、A7=13000,表9第6行第3列的新增3年期贷款额6。即:3=11800+13000+6。
将上述参数代入式(37),得:
(2000+7000+7)≤(11800+13000+6)
化简得:
76≤15800 (54)
同理8年期贷款8包括:表7第3列第10行的8年期贷款额A10=2000,表9第3列第8行的新增8年期贷款额8。即:8=2000+8。
将上述参数代入式(38),得
(2000+8)≤(2000+7000+7)
化简得:
87≤7000 (55)
综上,以式(44)作为目标函数,式(45)、式(47)-式(55)为约束条件,即建立了基于随机久期缺口控制的资产负债优化模型。
4.5.5 模型的求解
(1)本模型配置结果的求解
求解上文4.5.4的资产负债优化模型,得到求解后的资产配置结果列入表10第3列第1-8行,对应的目标函数值列入表10第3列第9行。
将表10第3列第1-8行代入式(45)的不等号左端,得到久期缺口:
D=0×2109.494+1.6450×8875.665+1.6450×3330.663+2.2638×3878.296+2.3129×3917.074+2.5347×4092.247+2.7506×4262.756+3.0938×4533.805-74043.34=-0.0029
(2)利率变化1%所引起的银行所有者权益变化
通过式(6)计算利率上升1%时所有者权益变化量。式(6)共有3个参数,其中:
将上述参数代入式(6),得到利率上升1%时、所引起的模型1结果的所有者权益变动,即:

列入表10第3列第10行。

表10 模型配置结果
4.6 对比分析
4.6.1 对比模型的定义
为了便于分析,首先定义三个模型。
定义模型1:本文构建的基于CIR模型的预留缺口的全资产负债模型。
定义模型2:令式(45)的久期缺口为零、其他条件不变得到的资产负债优化模型。
定义模型3:只考虑“增量”、不考虑“存量”的资产负债优化模型,则模型3与模型1存在以下不同:




三是在式(32)、式(34)、式(35)、式(36)、式(37)及式(38)的其他约束条件构建时,删除各式中的存量资产和存量负债。
4.6.2 模型2的计算
(1)模型2配置结果的求解
令式(45)为等式,即久期缺口为0,即:
0×1+1.64502+1.64503+2.26384+2.31295
+2.53476+2.75067+3.09388-74043.34=0 (59)
目标函数及其余约束条件与原模型相同,得到模型2。
以式(44)为目标函数,式(47)-(55)及式(59)为约束条件,进行规划求解,得到的配置结果列入表10第4列第1-8行,对应的目标函数值列入表10第4列第9行。
(2)利率变化1%所引起的银行所有者权益变化
仿照上文4.5.5中所有者权益变化的计算过程,将式(6)中第3个参数D=0、其他不变,代入式(6),得到利率变动1%时、所引起的模型2结果的所有者权益变动,列入表10第4列第10-11行。
4.6.3 模型3的计算
(1)随机久期缺口约束的确定
上文预测利率将上升,故式(56)中的不等号取小于号“<”,建立负缺口约束。
式(56)共涉及6个参数,其中:

将上述参数代入式(56)并化简,得到预留负缺口约束为:
1.6452+1.6453+2.26384+2.31295
+2.53476+2.75067+3.09388-61468.1<0 (60)
(2)资本充足率约束的确定
式(58)涉及3个参数,其中:

仿照上文4.5.3中式(30)的代入过程,将所有涉及到的参数代入式(57),得:
[6900-0.025962×35000×|(0×1+1.64502+1.64503+2.26384+2.31295+2.53476+2.75067+3.09388)-61468.1|]/(0×10×20×345678)≥11%
化简得:

(3)其他约束的确定
在式(32)、式(34)、式(35)、式(36)、式(37)及式(38)的其他约束条件构建时,删除式中的存量资产和存量负债,则有:
1≥35000×0.6% (63)
12345≥(10000+9000+7000+5000)×25% (64)
2≥35000×16.5% (65)
(13)≥35000×5% (66)
7≤6(67)
8≤7(68)
(4)模型3配置结果的求解
以式(44)为目标函数,式(48)、式(50)、式(60)、式(62)-(68)为约束条件,进行规划求解,得到的配置结果列入表10第5列第1-8行,对应的目标函数值列入表10第5列第9行。
(5)利率变化1%所引起的银行所有者权益变化
将表10第5列第1-8行代入式(60)的不等号左端,得到模型3的久期缺口:
D’=0×5295.019+1.6450×13723.42+1.6450×1540+2.2638×2506.715+2.3129×5043.543+2.5347×2591.911+2.7506×2480.629+3.0938×1818.767-61468.1=-0.033
仿照上文4.5.5中所有者权益变化的计算过程,将式(6)中第3个参数D’=-0.033、其他不变,代入式(6),得到利率变动1%时、所引起的模型3结果的所有者权益变动,列入表10第5列第10-11行。
4.6.4 对比分析结果
(1)模型1与模型2的对比
由表10第9行第3-4列可知,模型1的目标函数值为94.045,大于模型2的目标函数值、即91.799,说明模型1比模型2能为银行争取到更大的收益。
由表10第10行第3-4列可知,当对利率变化预测正确、即实际利率上升时,利率每上升1%、模型1的所有者权益增长333.5万元。而此时模型2的所有者权益并未增长,说明当利率发生有利变动时,模型1优于模型2。
由表10第11行第3-4列可知,当对利率变化预测错误、即实际利率下降时,利率每下降1%、模型1的所有者权益将会减少,但由于模型1在约束条件中体现了资本充足率,所以仍可满足银行对资本充足率的要求。
综上,相比于令久期缺口为0的资产负债模型,本文构建的基于预留缺口的资产负债优化模型,不仅能有效增加银行收益,还能在利率有利变动时增加所有者权益,并能在利率不利变动情况下仍满足资本充足率的约束。
(2)模型1与模型3的对比
由表10第9行第3列及第5列可知,模型1的目标函数值为94.045,优于模型3的目标函数值(72.46),说明相较于模型3,本文构建的模型1能为银行争取到更大的收益。
由表10第10-11行可知,虽然当利率变化预测正确、利率每上升1%,模型3的所有者权益能增长3795万元,但也应看到,实际利率每下降1%时、模型3的所有者权益损失则高达3795万元,占表10第5列第9行目标函数值、也即全部新增贷款利息收入的52%!意味着新增贷款利息收入的一半以上发生了损失。这说明模型3不能有效控制整体资产负债组合的利率风险。究其原因,就是因为模型3在建模时没有考虑巨额的存量资产负债。
综上,通过考虑存量与增量在内的全部资产负债组合的模型、即模型1,相较于只考虑增量、不考虑存量资产负债组合的对比模型、即模型3,不仅能有效增加银行收益,更能有效控制资产负债组合的整体利率风险。
5 结论
本研究的主要结论:
(1)本文以资产组合的收益最大为目标函数,预留随机久期缺口,并通过资本充足率约束久期缺口大小,构建了基于存量与增量的预留缺口资产负债优化模型。
(2)通过对比分析发现,相比于令久期缺口为0的资产负债模型,本文构建的基于预留缺口的资产负债优化模型,不仅能有效增加银行收益,还能在利率有利变动时增加所有者权益,并能在利率不利变动情况下仍满足资本充足率的约束。此外,本文建立的基于存量与增量全部资产负债组合风险控制模型,相较于只考虑增量、不考虑存量资产负债组合的对比模型,不仅能有效增加银行收益,更能有效控制资产负债组合的整体利率风险。
本研究的主要创新与特色:
一是以控制CIR利率期限结构的随机久期缺口为约束条件建立非线性规划模型、对资产配置进行利率风险免疫,反映了利率随时间的动态变化,突破了Macaulay久期、FW久期等现有研究的利率随时间的变化是固定不变或平行移动的限定条件,使资产配置的利率风险免疫更加符合现实情况。
二是建立了包括增量资产负债与存量资产负债的全资产负债优化配置模型,改变了现有资产负债模型大多只考虑增量资产负债、而忽略存量资产负债的弊端。事实上,增量资产相较于存量资产占比较小,银行家们真正关注的是包括存量和增量在内的全部资产负债组合的利率风险。
三是以市场利率朝着最不利方向变动时、预留缺口损失后的资本充足率仍然满足监管要求为约束条件,保证了在利率不利变动情况下损失仍在可控范围内,在利率有利变动时银行净值增加。
[1] Brewer E. Bank Gap Management and the Use of Financial Futures[J]. Economic Perspectives. 2008: 12-22.
[2] Charumathi B. Asset Liability Management in Indian Banking Industry - with special reference to Interest Rate Risk Management in ICICI Bank[J]. Lecture Notes in Engineering & Computer Science. 2008, 2171(1): 1-6.
[3] 杨婉茜,成力为. 基于Nelson-Siegel模型控制利率风险的资产负债组合优化模型[J]. 系统工程. 2014,32(2): 12-20.
Yang W Q, Cheng L W. An optimization model of asset-liability portfolio based on Nelson-Siegel model to control interest rate risk[J]. Systems Engineering. 2014,32(2): 12-20.
[4] Macaulay F R. The Movement of Interest Rates, Bond Yields and Stock Prices in the United States Since 1856[J]. General Information. 1938, 5(4): 474-489.
[5] 迟国泰,闫达文. 基于VaR控制预留缺口的资产负债管理优化模型[J]. 管理工程学报. 2011, 25(3): 123-132.
Chi G T, Yan D W. Asset and Liability Management Optimal Model based on VaR Preparation Duration Gap[J]. Journal of Industrial Engineering and Engineering Management. 2011, 25(3): 123-132.
[6] 迟国泰,许文,王化增. 兼控利率风险和流动性风险的资产负债组合优化模型[J]. 控制与决策. 2006, 21(12): 1407-1411.
Chi G T, Xv W, Wang H Z. Optimization Model of Asset-liability Portfolio Considering Interest Risk and Liquidity Risk[J]. Control and Decision. 2006, 21(12): 1407-1411.
[7] Fisher L, Weil R L. Coping with the Risk of Interest-Rate Fluctuations: Returns to Bondholders from Naïve and Optimal Strategies[J]. Journal of Business. 1971, 44(4): 408-431.
[8] Jacoby G. A Duration Model For Defaultable Bonds[J]. Social Science Electronic Publishing. 2010, 26(1): 129-146.
[9] 邓黎阳,孙刚. 商业银行利率风险测度方法的现实选择——Fisher-Weil久期模型的应用[J]. 国际金融研究. 2005(12): 4-11.
Deng L Y, Sun G. The practical choice of interest rate risk measurement method for commercial banks-the application of Fisher-Weilduration model[J]. Studies of International Finance. 2005(12): 4-11.
[10] 房启亮. 我国商业银行利率风险管理实证研究[D]. 沈阳:东北大学, 2008.
Fang Q L. Empirical Research on the Interest Risk in Chinese Commercial Bank[D]. Shenyang: Northeastern University, 2008.
[11] 闫达文. 基于信用与利率风险控制的银行资产负债优化模型研究[D]. 大连:大连理工大学, 2010.
Yan D W. The research on bank's assets and liabilities optimizaton models based on the control of credit risk and interest risk[D]. Dalian: Dalian University of Technology, 2010.
[12] 朱峰. Vasicek方向久期:一类新的利率风险免疫工具[J]. 金融监管研究. 2013(1): 69-79.
Zhu F. Vasicek direction duration: a new immune tool for interest rate risk[J]. Financial Regulation Research. 2013(1): 69-79.
[13] 刘艳萍,王婷婷,迟国泰. 基于方向久期利率风险免疫的资产负债组合优化模型[J]. 管理评论. 2009, 21(4): 11-25.
Liu Y P, Wang T T, Chi G T. An Empirical Study on Corporate Governance of China Commercial Banks with OverseasStrategic Investors[J]. Management Review. 2009, 21(4): 11-25.
[14] 吴灏文,迟国泰. 基于方向久期与凸度免疫的资产负债优化模型[J]. 系统工程学报. 2012, 27(4): 506-512.
Wu H W, Chi G T. Bank assets and liabilities optimization model based on the immunities of the directional duration and directional convexity[J]. Journal of Systems Engineering. 2012, 27(4): 506-512.
[15] 信怀义. 基于免疫策略的债券投资组合实证研究[J]. 经济与管理. 2017, 31(1): 51-57.
Xin H Y. The Empirical Research on Bond Investment Portfolio based on Immunization Strategy[J]. Economy and Management. 2017, 31(1): 51-57.
[16] Vasicek O. An equilibrium characterization of the term structure[J]. Journal of Financial Economics. 1977, 12(4): 627.
[17] 张志鹏. 随机久期利率免疫的银行全资产负债优化模型研究[D]. 大连:大连理工大学, 2016.
Zhang Z P. Research on optimization model of total assets and liabilities based on stochastic duration[D]. Dalian: Dalian University of Technology, 2016.
[18] Cox J C, Ingersoll J E, Ross S A. Duration and the Measurement of Basis Risk[J]. Journal of Business. 1979, 52(1): 51-61.
[19] 吴琼. 基于动态利率风险免疫银行资产负债优化模型[D]. 大连:大连理工大学, 2016.
Wu Q. Optimal model of asset-liability-management of bank based on the dynamic interest rate Immunization of Interest Rate Risk [D]. Dalian: Dalian University of Technology, 2016.
[20] 王克明,梁戍. 基于利率期限结构的随机久期与凸度模型构建及应用[J]. 统计与决策. 2010, 2010(24): 158-160.
Wang K M, Liang S. Construction and application of Stochastic Duration and convexity model based on term structure of interest rate[J]. Statistics and Decision. 2010, 2010(24): 158-160.
[21] 谢赤,邓艺颖. 固定收入债券利率风险管理中的持续期度量方法[J]. 湖南大学学报(自科版). 2003, 30(6): 105-109.
Xie C, Deng Y Y. The Duration Approach in the Interest Rate Risk Management[J]. Journal of Hunan University(Natural Sciences). 2003, 30(6): 105-109.
[22] 迟国泰. 银行资产负债管理优化理论、模型与应用[M]. 北京:科学出版社, 2014.
Chi G T. Model and Optimization of Bnak Assets and Liabilities Management[M]. Beijing: Science Press, 2014.
[23] 俞乔. 商业银行管理学[M]. 上海人民出版社, 1998.
Yu Q. Management of commercial banks[M]. Shanghai People's publishing house, 1998
[24] 闫达文,迟国泰,吴颢文. 资本充足率控制预留缺口的资产负债优化模型[J]. 运筹与管理. 2011, 20(2): 137-144.
Yan D W, Chi G T, Wu H W. Optimization Model of Asset-liability Portfolio Based on the Duration Gap Control of Capital Adequacy[J]. Operations Research And Management Science.2011, 20(2): 137-144.
[25] Chan K C, Karolyi G A, Longstaff F A, et al. An Empirical Comparison of Alternative Models of the Short‐Term Interest Rate[J]. Journal of Finance. 1992, 47(3): 1209-1227.
[26] 何晓群,刘文卿. 浅谈加权最小二乘法及其残差图——兼答孙小素副教授[J]. 统计研究. 2006, 23(4): 53-57.
He X Q, Liu W Q. Preliminary Discussion on Weighted Least Square Method and Its Residual Plot:Also Answering Associate Professor Sun Xiaosu [J]. Statistical Research. 2006, 23(4): 53-57.
[27] 范龙振,张国庆. 两因子CIR模型对上交所利率期限结构的实证研究[J]. 系统工程学报. 2005, 20(5): 447-453.
Fan L Z, Zhang G Q. Modeling term-structure of yields in SSE with two-factor CIR model[J]. Journal of Systems Engineering. 2005, 20(5): 447-453.
[28] 侯文琪,潘善宝. 基于单因素利率模型的SHIBOR利率行为实证研究[J]. 华东交通大学学报. 2013(4): 82-88.
Hou W Q, Pan S B. An empirical study on SHIBOR with Single-factor Term Structure of Interest Rate models[J]. Journal of East China Jiaotong University. 2013(4): 82-88.
[29] 陈雯,陈浪南. 国债利率期限结构:建模与实证[J]. 世界经济. 2000(8): 24-28.
Chen W, Chen L N. Term structure of national debt interest rate: Modeling and demonstration[J]. The Journal of World Economy. 2000(8): 24-28.
[30] 李湘鸣. SPSS软件应用指导[M]. 南京:东南大学出版社, 2000.
Li X M. SPSS software application guidance [M]. Nanjing: Southeast University Press, 2000
[31] 中国人民银行. 中国人民银行决定下调存款准备金率[EB/OL]. http://www.pbc.gov.cn/zhengcehuobisi/125207/125213/125434/125798/3023454/index.html.
The People's Bank of China and The People's Bank of China decided to reduce the deposit reserve ratio [EB / OL] http://www.pbc.gov.cn/zhengcehuobisi/125207/125213/125434/125798/3023454/index.html.
Optimization model of assets and liabilities management based on stochastic duration gap
CHI Guotai, ZHANG Zhipeng, LIU Yan
(Faculty of Management and Economics of Dalian University of Technology, Dalian 116024, China)
Asset-Liability Management (ALM) is to achieve an optimal allocation of assets under the constraints on the number and structure of the liabilities, to realize the maximization return of the portfolio by pursuing assets liquidity, profitability, and safety. Since the assets are equal to liabilities plus the owners' equity, the value of the assets and liabilities of banks changes correspondingly when the interest rates change, and the changes of the two cannot always be the same. Therefore, the value of the owner's equity will inevitably change. Therefore, interest rate risk is one of the risks that must be controlled in asset-liability management. Moreover, in the operation of banks, the loan interest rate is not fixed but is characterized by volatility and randomness. Macaulay duration or static NS duration model cannot accurately identify the random change of the real interest rate.
The first part of this paper gives the stochastic duration function based on the dynamic interest rate term structure of CIR. Thus we consider the dynamic change of the interest rate over time and ameliorate the existing research like Macaulay and F-W duration that interest rates are fixed or in parallel movements. Thus, the interest rate risk immunization can be more in line with reality. By taking into consideration of the existing portfolio risk and increment portfolio risk, we improve the existing research that ignores the interest risk of stock assets and liabilities when performing asset allocation. By reserving a duration gap rather than making a gap of zero, the bank owner's equity is increased when interest rates change favorably, and the bank's capital adequacy ratio can still meet regulatory requirements when interest rates are adversely changed.
In the second part, the method of determining parameters of both the CIR model and the stochastic duration is given. It includes the steps of estimating the parameters of the CIR model with the discrete method, fitting the relationship between the market interest rate and termby an exponential function, and determining the parameters such as cash flow during the stochastic duration calculation.
The third part of this paper gives the asset-liability optimization model. Taking the maximum of the interest income of the bank as the objective function, a non-linear programming model is established by controlling the interest rate risk of all the assets and liabilities, including the stock and increment, through the constraint of the capital adequacy ratio controlling the stochastic duration gap size, supplemented by the statutory deposit reserve and other regulatory requirements. Thus, the optimal allocation of assets can be obtained.
The fourth part is an empirical study. The empirical results demonstrate that the total asset-liability model based on the CIR model can effectively control the interest rate risk. When compared with Model 2, which makes the duration gap equals 0, the model constructed in this paper not only can effectively increase the bank's income, but also can increase the owner's equity when the interest rate is favorable, and can still satisfy the restriction of the capital adequacy ratio under the unfavorable interest rate change. Compared with the Model 3, which only considers increment and does not consider the stock assets and liabilities, the model we constructed can not only effectively increase the bank's income, but also effectively control the overall interest risk of all the assets and liabilities.
In summary, based on the CIR dynamic term structure model, we obtain the stochastic duration and reserve the duration gap of all the assets and liabilities, including the increment and the stock. We constrain the duration gap to an acceptable level and build the asset-liability optimization model to control the interest rate risk. The empirical results show that the model we constructed can effectively control the interest rate risk of the total asset and liability portfolio, and it outperforms the model with zero gaps, and the model only considers the increment portfolio.
Bank asset-liability management; Interest rate risk controlling; Stochastic duration; CIR model; Total asset and liability portfolio
2017-12-20
2018-05-13
F830.33,O221.1
A
1004-6062(2020)03-0199-015
10.13587/j.cnki.jieem.2020.03.021
2017-12-20
2018-05-13
国家自然科学基金资助项目(71471027、71731003);国家社科基金一般项目(16BTJ017);辽宁经济社会发展重点课题(2015lslktzdian-05);辽宁省社科规划基金项目(L16BJY016)
迟国泰(1955—),男,黑龙江海伦县人;大连理工大学管理与经济学部教授,博士;研究方向是银行资产负债管理、金融风险管理。
Funded Project:Supported by the National Natural Science Foundation of China (71471027, 71731003), the National Social Science Foundation of China (16BTJ017), the Key Project of Economic and Social Development of Liaoning Province (2015lslktzdian-05) and the Social Science Planning of Liaoning Province (L16BJY016)
中文编辑:杜 健;英文编辑:Charlie C. Chen
