坡面径流阻力计算模式对比研究
2020-05-21余明辉
胡 鹏,余明辉
(武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072)
1 研究背景
坡面流是指降雨或融雪在扣除地面截留、填洼与下渗等损失后在重力作用下沿坡面表层流动的一种特殊水流,有时也包括雨水在坡面上部下渗后,经过表层土壤,以壤中流的形式在坡面下部复而流出地面,再度形成的一种片状水流。坡面流水力特性取决于许多因素,如降水强度和历时、土壤质地或种类、前期水分条件、植被密度和类型、地貌特性包括洼坑和小丘数量和大小、坡度和坡长、边界稳定性条件[1]。作为水流污染物迁移、土壤侵蚀及泥沙输移的主要动力因素,不同边界条件下坡面流的形成、发展过程是该领域的研究基础。
随着计算机技术和计算方法的迅速发展,坡面流的数值模拟求解越来越受到重视。作为坡面径流模型中重要的参数,阻力系数是影响坡面流计算精度的关键参数[2-3]。对坡面流阻力特性研究主要是通过野外和实验室内的放水或降雨模拟试验,根据实验结果应用回归分析等方法建立阻力系数与雷诺数、降雨强度、土壤粒径、坡度等因子的表达式,如姚文艺[4]、Abrahams等[5]、Hirsch[6]、Hu等[7]和Lawrence[8]建立了形式各异的阻力系数公式。Zhang 等[9]将坡面上阻力的处理分为三种类型:阻力系数为常数;不同土地类型、地表覆盖情况、耕作措施而采用不同阻力系数;考虑阻力系数的空间非均匀性,即其在每个网格的变化。由于坡面流阻力受土壤类型、植被覆盖、床面粗糙度及降雨影响等众多因素影响,难以从理论上描述,大多数水文模型中,仍将阻力系数作为常数处理。尽管阻力系数为常数使用较广泛,但其选取具有较强的经验性,越来越多的研究关注阻力的空间非均匀性对坡面汇流的影响[10-11]。
综上所述,现有成果尽管在坡面流阻力特性研究上取得了一些成果,但由于试验条件的差异,简化处理方法不同,建立的阻力公式仍有很大局限性,不便于应用。本文选取三种有代表性的阻力模式,即阻力系数为常数、基于阻力线性叠加原理的阻力分割模型、以淹没度为变量的Lawrence 模型,对其在裸坡、有砾石覆盖坡面、有植被覆盖坡面等三种典型坡面的坡面径流计算精度的影响规律展开研究,并对植被覆盖坡面,探究降雨强度对不同阻力模式模拟结果间差异的影响。
2 研究方法和计算模式
为研究不同阻力模式在坡面上的适用性,本文建立了坡面降雨径流数学模型,对形成坡面径流的两个主要过程降雨入渗和坡面汇流进行模拟。降雨入渗模型采用考虑坡度影响的Green-Ampt 模型,可完整模拟降雨入渗过程,得到入渗率随时间变化曲线。坡面径流模型采用扩散波模型,可模拟坡面汇流过程,得到坡面各水力要素的时空变化过程。模型的离散求解采用具有二阶精度的Maccormark 有限差分格式,网格划分与时间步长选取满足柯朗数小于1 的条件。模型中选取了三种不同的阻力模式,对不同类型坡面进行了模拟,并将不同阻力模式得到的模拟值与实测值比较分析。
2.1 坡面降雨入渗模型Green-Ampt 模型是最早基于物理过程和毛管理论的入渗模型,运用Darcy定律得到入渗率和入渗量之间的关系及其随时间的变化过程,能较好地考虑土壤饱和导水率、有效孔隙率、初始含水量和累计入渗量对入渗过程的影响。经典Green-Ampt 模型仅适用于平坡入渗,由于坡面坡度较大,用其求解坡面入渗过程会引入一定的误差。因此采用Chen 和Young 提出的考虑坡度对于土壤入渗的影响的改进模型[12]。
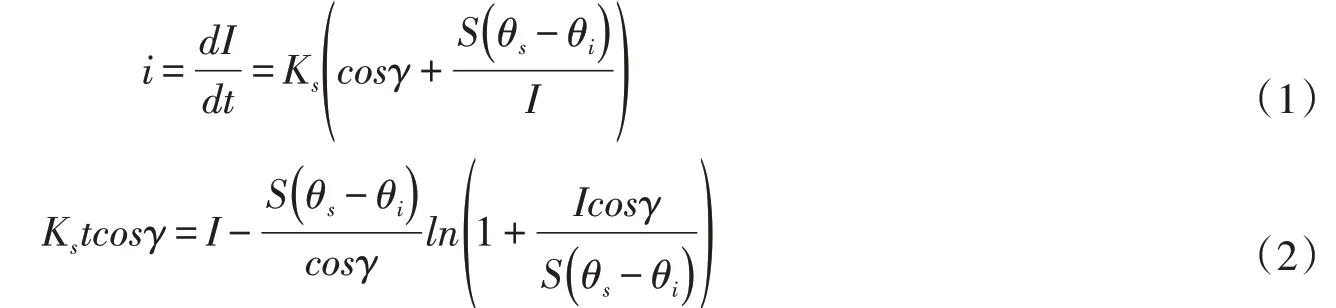
式中:i为入渗率,m/s;Ks为土壤饱和导水率,m/s;S为土壤吸力,m;I为累计入渗量,m;θs为土壤饱和含水率;θi为土壤初始含水率;γ为坡面倾角,°。
整个降雨入渗过程的入渗率可描述为:
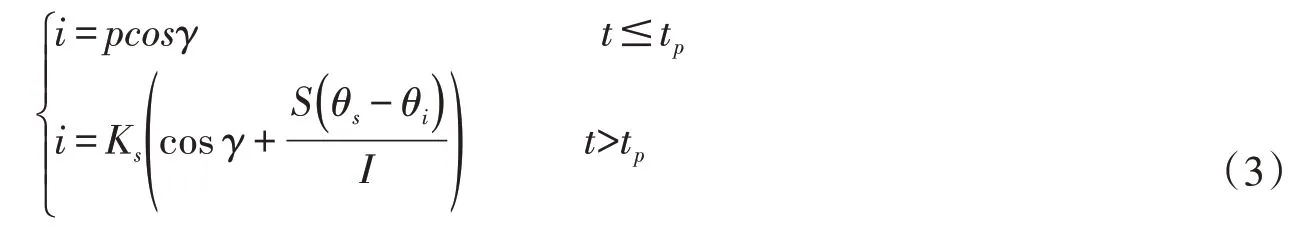
式中:p为降雨强度,mm/h;tp为开始积水时间,tp=Ip p;Ip为累计入渗量临界值,当i=pcosγ时,由下式推出Ip计算公式:

I为积水开始后的累计入渗量,也包括未积水时段的入渗量在内。由于不是从t=0时刻开始积水,I的计算须采用修正后的公式:
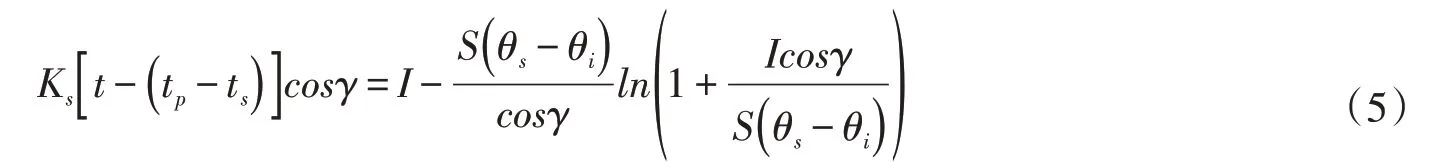
式中:ts为假设由t=0开始积水到入渗率i=p时所需的时间,可以理解为一个虚拟时间,s,计算公式如下:
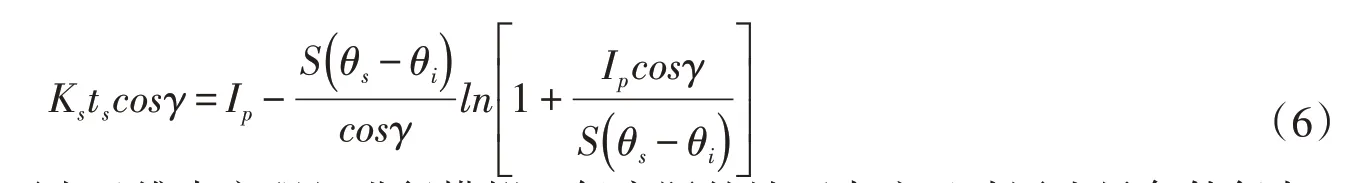
2.2 坡面径流模型坡面径流可由圣维南方程组进行模拟。但实际的坡面水流运动因边界条件复杂,同时,由于坡面流水深很浅,在实际坡面流动中受微地貌影响很大,完整的圣维南方程组并不一定能够很好地描述这种特殊的流动。简化的圣维南方程即运动波与扩散波模型被广泛的应用于坡面流模拟中,扩散波模型包括连续方程与动量方程,可表示如下[13]:

式中:h为水深,m;t为时间,s;p为降雨强度,m/s;i为入渗率,m/s;Sf为能坡;S0为坡面比降;x为沿坡面向下坐标;q为单宽流量,q=hu,m2/s;u为流速,m/s。
u可由Darcy-Weisbach公式计算:

式中:f为Darcy-Weisbach阻力系数;R为水力半径。
2.3 阻力模式Darcy-Weisbach 阻力系数f是无量纲参数且有一定的理论基础,大部分学者选择f对坡面流阻力特性研究进行研究,蒋昌波等[14]和Abrahams 等[15]也认为f比Chezy 系数和Manning 糙率系数更适合描述坡面地表水流的阻力。本文选取了下面三种阻力模式:
阻力系数为常数:

Lawrence 模型:Lawrence 以淹没度为变量,提出可将坡面流分为完全淹没、临界淹没和部分淹没三种状态。完全淹没时,基于紊流理论计算阻力;临界淹没时,假定掺长与特征粗糙度成正比关系;部分淹没时,仅考虑粗糙单元的拖曳力,分别推导建立了三种状态下阻力系数表达式[8]:
完全淹没:
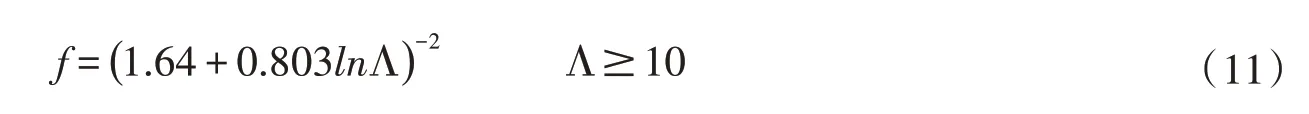
临界淹没:
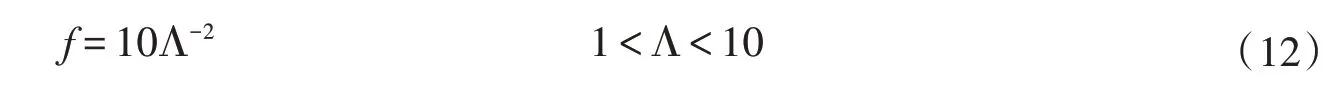
部分淹没:
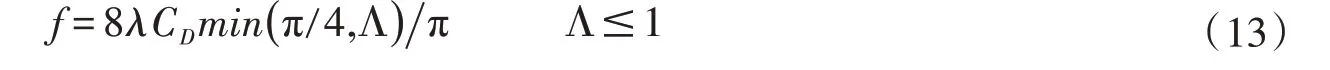
式中:Λ为淹没度,Λ=h Dr;h为水深;Dr为特征粗糙尺度;λ为床面粗糙单元的覆盖率,%;CD为系数。
阻力分割模型:在坡面流阻力研究特性研究中,阻力线性叠加原理得到了广泛应用,Abrahams提出根据地表特征差异将坡面流阻力分为4部分,降雨阻力、颗粒阻力、形态阻力和波阻力,通过阻力的线性叠加得到综合阻力。根据Abrahams,Hirsch 的系列试验结果,Hu 等人运用量纲分析与回归分析得到了部分阻力计算公式[5,7]。降雨阻力公式采用Shen的试验结果[16]:
降雨阻力:

颗粒阻力:

形态阻力:

波阻力:

综合阻力:

式中:p为降雨强 度,mm/min;Re为 雷诺数,Re=uh υ,υ为运 动 黏度,m2/s;Fr为 弗 劳德数,g为重力加速度,m/s2。
3 计算结果与分析
裸坡、有砾石覆盖坡面、有植被覆盖坡面为三种常见坡面类型,用上述三种不同阻力模式的降雨径流模型对各类型坡面进行模拟,将数值模拟结果与实测值进行比较分析。裸坡上试验数据分别采用中国科学院水土保持研究所和Abban 分别进行的室内人工降雨—入渗—径流试验数据,试验中土样分别为黄土和粉质壤土[17-18]。砾石是指平均粒径大于2 mm 小于64 mm 岩石或矿物碎屑物,砾石覆盖坡面常见于沙漠地带,有砾石覆盖坡面采用Jomaa 进行的室内实验数据,砾石的覆盖度为20%,粒径5 ~7 cm[19]。植被有明显的阻水滞流拦沙作用,因此植被过滤带常被用于坡面防护。植被冠层对降雨有截留能力,因此需考虑植被蓄水能力,有植被覆盖坡面采用Neibling进行的场地实验,距坡脚2.5 m 范围内有植被覆盖,植被覆盖率为40%。上述试验中土样均采用当地具有代表性土壤,经测定其性质后进行实验,降雨均采用人工降雨模拟装置,保持降雨强度均匀,降雨强度均取当地降雨的典型代表值,坡面入口处无来流,坡面出口自由出流,能很好的反映天然实际情况。各试验坡度均在缓坡范围内,对不同长度的坡长模拟对比结果分析也表明不同坡长下不同阻力模型对模拟结果的影响规律相一致,因此可认为试验坡长具有一定的代表性。试验过程中流量由尾部集流装置定时取样测量,流速测量采用染色剂法测得表面流速乘以修正系数即可得断面平均流速。从整体上看,可认为各试验具有一定的代表性与可比性。各坡面基本参数见表1。

表1 各坡面基本参数
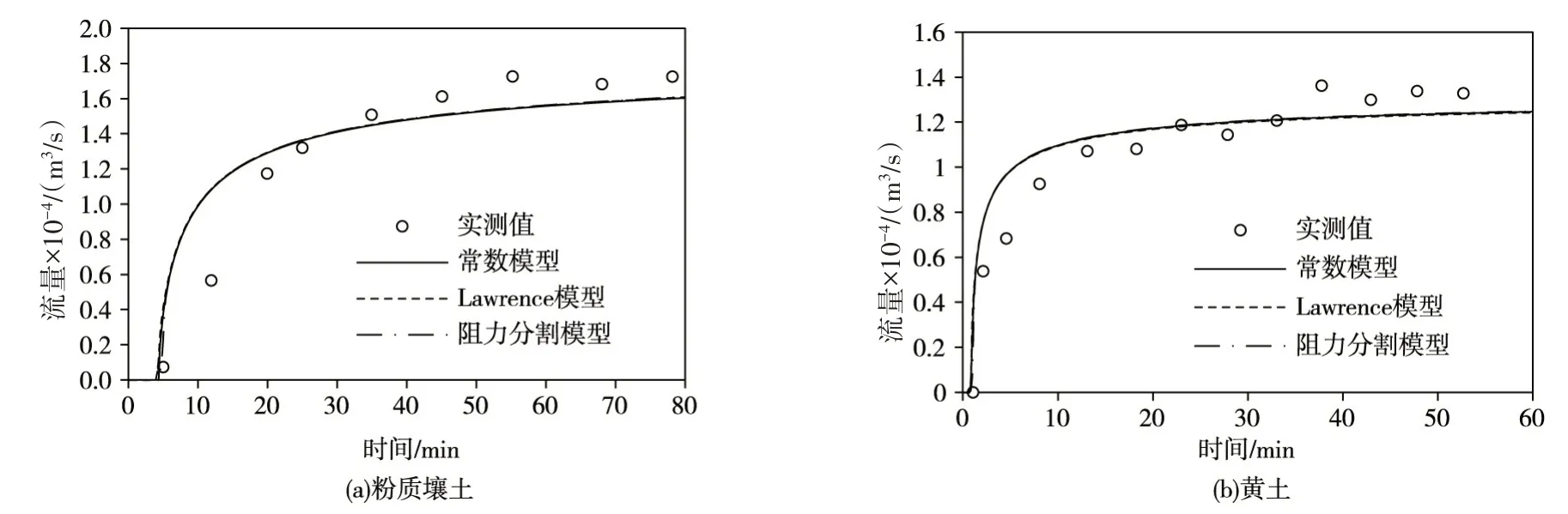
图1 裸坡出口实测流量与计算流量对比
图1—3 为各类型坡面流模拟出口流量过程与实测值对比图。由图可知,在裸坡上,无论是黄土还是粉质壤土,各阻力模式计算得到的流量过程并无差异,且均与实测资料吻合较好。在有砾石覆盖坡面上与有植被覆盖坡面上,涨水阶段各模式模拟结果有较大差别,阻力不仅仅会因为边界条件改变而变化,也会随水深,流速等水力要素变化而改变,故阻力与水力要素间是互相影响的,且是一个复杂的动态过程,考虑了阻力时空变化的阻力分割模式计算结果与实测资料最吻合,由于Lawrence 模型在水深较小,即淹没度较小的时候,由于其只考虑绕流阻力,会低估阻力系数,所以模拟流量值高于实测值。在坡面汇流的稳定阶段,可以发现各模式计算结果差别不大,此时,坡面流流量主要由降雨强度与入渗量决定,受阻力系数影响不大,这是由于达到稳定阶段后,坡面各水力要素随时间变化很小,一个时间步长内相差不大,因此由水力要素计算得到的阻力系数也几乎不变,由坡面径流模型中的连续性方程与动量方程可知,此时决定坡面流流量的关键主要是源项,即降雨量与入渗量。Huang 等[10]研究空间变化的阻力系数对流量过程影响时也得到了阻力系数对坡面径流流量的影响在坡面汇流的涨水与退水阶段较大,而在稳定阶段影响较小这一结论。对有植被覆盖坡面,模拟了其退水阶段,由图3 可知,常数模型及阻力分割模型和实测值吻合较好,但由于Lawrence 模型只考虑淹没度这个单一变量,在退水阶段会低估退水时间。

图2 砾石覆盖坡面出口流量与计算流量对比
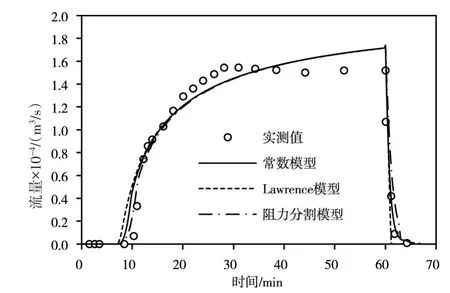
图3 植被覆盖坡面出口流量与计算流量对比
阻力模式的选取不仅影响坡面径流流量过程,也会影响坡面径流流速的模拟结果,坡面径流流速与污染物迁移,泥沙侵蚀过程密切相关,因此有必要对不同阻力模式下的流速模拟结果进行讨论。裸坡上模拟的出口流速过程与实测值对比见图4,从总体上看,阻力分割模型模拟效果最好,在初始涨水阶段,常数模型与实测值更为接近,而达到稳定阶段后,流速模拟值偏低,这是由于随着水深的增大,阻力系数应变小,而常数模型并不能体现这一特性,这与Mügler 等[20]在研究坡面径流模拟与污染物迁移时得出的阻力系数为常数的数学模型会低估最大流速结论一致。尽管在裸坡上Law⁃rence 模型模拟流量过程并无差别,但是流速模拟值较实测值总体偏高。
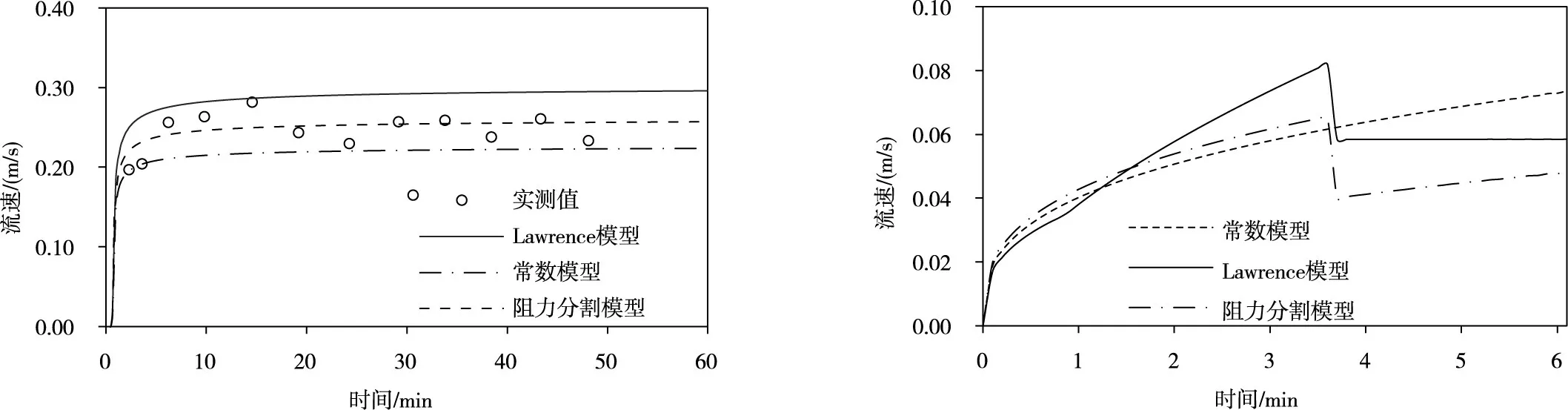
图4 出口流速与实测值对比

图5 流速沿程变化
图5 为有植被覆盖坡面在40 min 时坡面流速沿程分布。常数模型模拟流速沿程增大,最大流速在坡脚,阻力分割模型与Lawrence 模型模拟流速最大值并不是在坡脚,而是出现在植被覆盖区域上部,很好地体现植被的滞流效应,这与杨春霞等[21]和孙佳美等[22]研究植被覆盖对坡面产流产沙影响时得到的实验结果相符合。
4 讨论
坡面水文过程的发生主要动力来自于降雨,降雨强度会影响坡面的下渗过程,产流的时间,坡面径流流量以及达到稳定阶段时间。对于同一坡面,随着降雨强度的增大,其涨水阶段时间会减少,径流流量增大,从而导致不同阻力计算模式下坡面径流流量模拟结果间差异减小,但当差异减少至一定程度趋于稳定后,即使降雨强度增大,差异值也不再改变,将这一分界点定义为降雨强度阈值。对于不同坡面,降雨强度阈值会随坡长、坡度以及植被覆盖度变化而改变,因此有必要研究其变化规律。在有植被覆盖的坡面,不同的阻力模式对坡面流流量模拟结果有较大影响,考虑时空变化的阻力系数的阻力分割模式与实测值吻合最好,为探究降雨强度对不同阻力模式模拟结果的影响,将阻力分割模式计算得到的结果作为标准值,通过分析不同降雨强度下阻力系数常数模型与阻力分割模型计算结果间的Nash-Sutcliffe 效率系数,确定降雨强度阈值。大于阈值时,不同阻力模式对计算结果影响甚微;反之,不同阻力模式计算差异较大,需选择合适的阻力计算模式。
Nash-Sutcliffe效率系数计算公式为[23]:

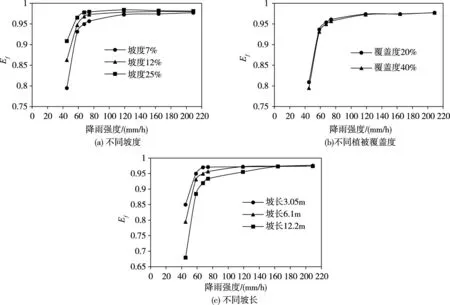
图6 Ef 与降雨强度关系
式中:Ef为Nash-Sutcliffe效率系数;Oj为测量值;Mj为模拟值;Oˉ为均值;n为时间点个数。
Ef值越接近1代表模拟值与实测值越吻合。
图6(a)为固定坡长与植被覆盖率条件下,坡度分别为7%、12%和25%时,根据模拟结果计算得到的Nash-Sutcliffe 效率系数与降雨强度间关系图。图中存在明显转折点,随着降雨强度的增大,E f值不发生变化,且E f值接近1,说明模拟结果相差很小,转折点的降雨强度即为降雨强度阈值。Pa⁃panicolaou 等通过研究坡面径流功率与降雨强度关系,也发现坡面上存在临界降雨强度,大于临界降雨强度时,坡面阻力特性对坡面径流模拟影响较小,几乎可忽略不计[11]。在坡度为7%时,降雨强度阈值为119 mm/h,在坡度为12%时,降雨强度阈值为74 mm/h,在坡度为25%时,降雨强度阈值为67.5 mm/h。在坡长一定条件下,坡度越缓,其降雨强度阈值越大。比较同一降雨强度下不同坡度情况下的Nash-Sutcliffe 效率系数,也可发现坡度越大,Nash-Sutcliffe 效率系数也越高,即不同阻力模型对计算结果影响更小。
图6(b)为固定坡长与坡度条件下,植被覆盖度为20%和40%时,根据模拟结果计算得到的Nash-Sutcliffe 效率系数与降雨强度间关系图。由图可知,不同植被覆盖度对降雨强度阈值影响不大,均在119 mm/h 左右。在同一降雨强度下,植被覆盖度越低,Nash-Sutcliffe 效率系数略高,不同阻力模型对计算结果影响略小。
图6(c)为固定坡度与植被覆盖度条件下,坡长分别为3.05 m、6.1 m 和12.2 m 时,根据模拟结果计算得到的Nash-Sutcliffe 效率系数与降雨强度间关系图。在坡长为3.05 m 时,其降雨强度阈值为67.5 mm/h;在坡长为6.1 m时,其降雨强度阈值为119 mm/h;在坡长为12.2 m时,其降雨强度阈值为164 mm/h。在坡度一定条件下,坡长越大,其降雨强度阈值越大。比较同一降雨强度下不同坡长情况下的Nash-Sutcliffe 效率系数,也可发现坡长越长,Nash-Sutcliffe 效率系数越小,即阻力模式的选取对计算结果影响越大。
5 结论
基于降雨径流数学模型,研究了不同阻力模式对坡面汇流计算结果的影响,可得出以下结论:(1)在裸坡上,不同阻力模式坡面流流量模拟结果差别很小,流速模拟结果表明阻力分割模型与实际更吻合,阻力系数为常数模型会低估最大流速,而Lawrence 模型模拟流速值较实测值总体偏高;在有砾石覆盖和植被覆盖的坡面上,考虑了阻力系数时空变化的阻力分割模型模拟精度最高,且能体现植被的滞流效应。从整体上看,阻力系数对坡面径流流量模拟的影响在坡面汇流的涨水与退水阶段较大,而在稳定阶段很小。(2)对有植被覆盖的坡面,存在降雨强度阈值,大于阈值时,不同阻力模式对计算结果影响甚微;反之,需选择合适的阻力计算模式。并且坡度坡长是影响降雨强度阈值的关键因子,坡长越长,坡度越缓,其降雨强度阈值越大。
