降雨入渗对浅埋黄土隧道稳定性的影响

邓祥辉，曹卫平，杨东升

(西安工业大学 建筑工程学院,西安 710021)

中国黄土分布广泛，大量建设工程不可避免地要修建在黄土地区。当隧道穿越浅层黄土中的Q4、Q3期黄土时，由于新黄土孔隙率大、湿陷性显著，隧道施工扰动极易引起各种工程问题[1-2]。特别是降雨产生的地表水入渗后，黄土隧道进、出口段以及浅埋段容易发生大变形、局部坍塌，甚至塌方等工程事故。因此，有必要深入研究降雨入渗作用下浅埋黄土隧道的结构稳定性。

目前，考虑降雨入渗对黄土隧道稳定性影响主要涉及三方面的研究：一是黄土渗流理论和模型研究；二是不同含水率的黄土力学特性研究；三是降雨入渗影响范围以及黄土隧道稳定性分析。渗流理论早期主要以Darcy定理为基础，将黄土视为孔隙介质。后续研究中，许多学者建立了专门的降雨入渗模型，其中应用最广泛的是Mein-Larson模型[3-4]。近年来，很多学者将优先流理论应用于黄土地层。如张中彬等[5]系统分析了黄土孔隙对优先流的影响，并总结了优先流定量化和数学模拟研究进展，指出受黄土结构复杂性影响，优先流理论在黄土中的应用还有诸多问题。在不同含水率黄土力学特性研究方面，陈正汉等[6]以压实黄土为研究对象，系统研究了非饱和土的力学特性在剪切过程中的变化规律，并对非饱和土水气运移的测试方法进行了研究。黄琨等[7]通过直剪试验研究了黄土抗剪强度与含水率的关系，发现黏聚力与含水率的关系可以用两段直线表示，当黄土达到一定含水率时，黏聚力急剧降低。梅岭等[8]通过试验指出脱水与吸水两种情况中，试样含水率随基质吸力变化的规律有所不同。邓洪亮等[9]通过大量浸水试验研究了黄土湿陷性与浸水时间、饱和度、含水率、压力间的关系。近年，在降雨入渗影响范围以及黄土隧道稳定性分析方面也取得了一些进展。如宋孝玉等[10]、张常亮等[11]进行了现场试验，研究了不同渗流强度、时间等因素的影响，发现新黄土中水分渗流速率较快，影响深度虽然会随降雨强度的提高而增加，但一般不会超过6 m的极限入渗深度，且极限深度与黄土所处区域密切相关。赖金星等[12]基于流固耦合理论，建立了隧道开挖流固耦合模型，分析了塑性区范围与排水方案有关系。Yoo等[13-14]采用流固耦合法分析了地下水渗流情况下隧道施工引起的土体沉降。王浩然等[15]通过数值模拟研究了渗流对隧道开挖面稳定上限的影响，分析了渗流对开挖面稳定性影响的因素和破坏模式。

目前，对黄土渗流模型、黄土非饱和特性、降雨入渗影响范围以及黄土隧道稳定性等方面均进行了研究[16]，但很少考虑依托实际黄土隧道工程建立基于黄土的弹塑性增量本构关系，也未考虑降雨入渗后饱和黄土地层和含水率增加地层对隧道稳定性的影响。鉴于此，笔者首先对不同含水率的隧道围岩黄土试样进行三轴试验，建立黄土的弹塑性增量本构关系；然后将建立的本构关系导入Midas数值模拟软件，应用渗流-应力耦合模块分析降雨入渗对浅埋黄土隧道稳定性的影响，并进行了工程验证。

1 围岩黄土三轴试验

试验黄土试样取自某隧道掌子面的Q3期原状黄土，在新开挖的黄土隧道掌子面中心1 m2的范围内，将周边土体掏空，将中心未扰动土体完整取出，制成300 mm×300 mm×200 mm的块体。为避免土样的扰动，对土样进行胶带密封、隔水包装运输至实验室，将未破坏的完整土体用削土器削制成高为200 mm、直径为60 mm的圆柱体试验土样。测得自然状态下含水率为18%，饱和含水率为30%，其他物理指标如表1所示。对制备好的土样均匀喷雾加湿，之后放在保湿缸内保湿2 h，称量质量，重复该步骤直至土样含水率达到4种试验含水率(18%、22%、26%、30%)。为获得非饱和土的应力-应变关系、力学参数及峰值强度等，对试样按含水率的不同进行分组，每组分别进行剪切试验和等压试验。

表1 隧道围岩黄土试样的初始物理指标Table 1 Initial physical parameters of undisturbed loess samples

1.1 试验参数及试样分组

1.1.1 剪切试验 试件在排水剪切试验前，进行24 h的固结。三轴试验中，剪切速率为0.025 mm/min，最大围压为300 kPa，最小为50 kPa，最大和最小围压中50 kPa为一档，共进行6种不同围压的试验。结束试验条件为：轴向应变达到15%或试件完全破坏。此时，可获得试件峰值强度和残余强度。

1.1.2 等压试验 试验控制条件为每隔24 h加一级荷载。从0 kPa加载至100 kPa时，每级荷载为25 kPa；从100 kPa加载至300 kPa时，每级荷载为50 kPa。试验时记录每级压力和体变。

将试样制作成含水率分别为18%、22%、26%、30%的4组，分别记为1、2、3和4组。每组按照围压设置需要，进行6次剪切试验和1次等压试验。每组7块试样，用数字1～7标记每块试样。共需要28块试样。

1.2 破坏形态分析

三轴剪切试验中，记录试样的破坏形态，并按含水率进行分组，其中，HT代表试样破坏前，HTP代表破坏后。受篇幅限制，只展示破坏规律最明显3组试样，如图1～图3所示。

图1 含水率18%试样破坏前后对比Fig.1 Comparison of samples with water content of 18% before and after

图2 含水率22%试样破坏前后对比Fig.2 Comparison of samples with water content of 22% before and after

图3 含水率30%试样破坏前后对比Fig.3 Comparison of samples with water content of 30% before and after destruction

从图1～图3可见，含水率与破坏形态密切相关，即含水率越低试样破坏程度越大；而围压与破坏形态呈正相关，即围压越高，剪切带长度越长，破碎越严重。从试验现象可见：

1)同一含水率条件下，破坏程度随固结压力的增大而增大。主要原因是固结压力较高时，黄土受挤压而压密，形成新的次生结构，新的黏聚力使剪切破坏更为明显。

2)在同一固结围压下，含水率越大，破坏程度越小。主要原因是随着含水率增加，颗粒间胶结物间距增大，胶结强度减小；同时，颗粒间吸附水膜变厚，凝聚强度降低和摩擦系数变小，此时试样更容易产生塑性变形而非直接破坏[17-18]。当试样含水率增大至饱和时，情况更加明显，试样破坏时基本不会出现剪切面。

3)力学指标均随含水率增大而减小，弹性模量和黏聚力从自然状态至饱和状态分别降低43%和62%，而内摩擦角受影响相对较小，仅降低16%。

1.3 应力-应变关系分析

根据试验情况，通过三轴仪读取并记录试验过程中的应力、应变值，绘制应力-应变曲线。每次剪切试验中保持围压σ3不变，增大轴向力σ1，与隧道围岩受力过程中的上部受压或下部卸荷情况一致，剪切试验的应力-应变曲线如图4所示。

图4 剪切试验应力-应变曲线图Fig.4 Stress-strain curve of shear test

由图4可见，随着试样含水率的增加，抗剪强度总体呈逐渐降低的趋势，但在应力-应变曲线中的直线段，直线的斜率随着围压增加而变大，说明围压的大小对黄土的抗剪能力至关重要。从试验过程看，试样应变达到2%时开始屈服，当应变量达到4%左右时结束。此时抗剪能力基本由围压提供。此外，试验中围压越大，屈服的起始应变量越小，说明固结过程虽然提高了试样的抗剪能力，但对土的结构性产生了一定的破坏，使其弹性在剪切过程中被更快速地消耗。另外，在相同围压下，试样弹性模量随着含水率增加而明显降低，主要原因是原生结构中部分胶结物质的溶解。但是，每组试样的弹性应变均能够持续2%左右，可见，保持黄土弹性上限的关键因素是黄土的颗粒排列情况，而含水率的增加对此影响不大。

当含水率超过中值含水率，达到26%时，试样的屈服过程明显加快，即同样剪切量能承受的剪应力大大降低。当试样含水率较大时(后两种含水率)，剪应力在试验中发生了明显降低的过程，即试样被完全破坏，塑性也完全丧失的情况。由此可见，含水率增加的影响贯穿于整个剪应力-应变过程。

1.4 土体抗剪参数

通过三轴剪切试验，绘制摩尔应力圆，得不同含水率下土体的抗剪参数如表2。由表2可知，含水率增加对黄土的黏聚力影响非常大，而对内摩擦角的影响较小，含水率增加后试样弹性阶段的抗剪能力大大降低，但此阶段的总应变量基本保持不变，这是因为含水率增加主要稀释了黄土的胶结物质，而对颗粒排列扰动较小。

表2 不同含水率试样的抗剪参数Table 2 Shear parameters of samples with different moisture content

2 建立本构关系

首先基于Hooke定理计算出整个变形中弹性变形和塑性变形；然后假设塑性变形满足Drucker 公设，通过应力-应变曲线的规律，拟合得到屈服函数和其他所需参数，建立弹塑性增量本构关系。

2.1 屈服面的确定

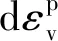
(1)

将试验结果绘制在p-q坐标中，拟合结果如图5所示。从图5可见，屈服轨迹大体上呈椭圆状。因此，可用椭圆曲线进行拟合，拟合公式为

(2)

式中：h为硬化参数。

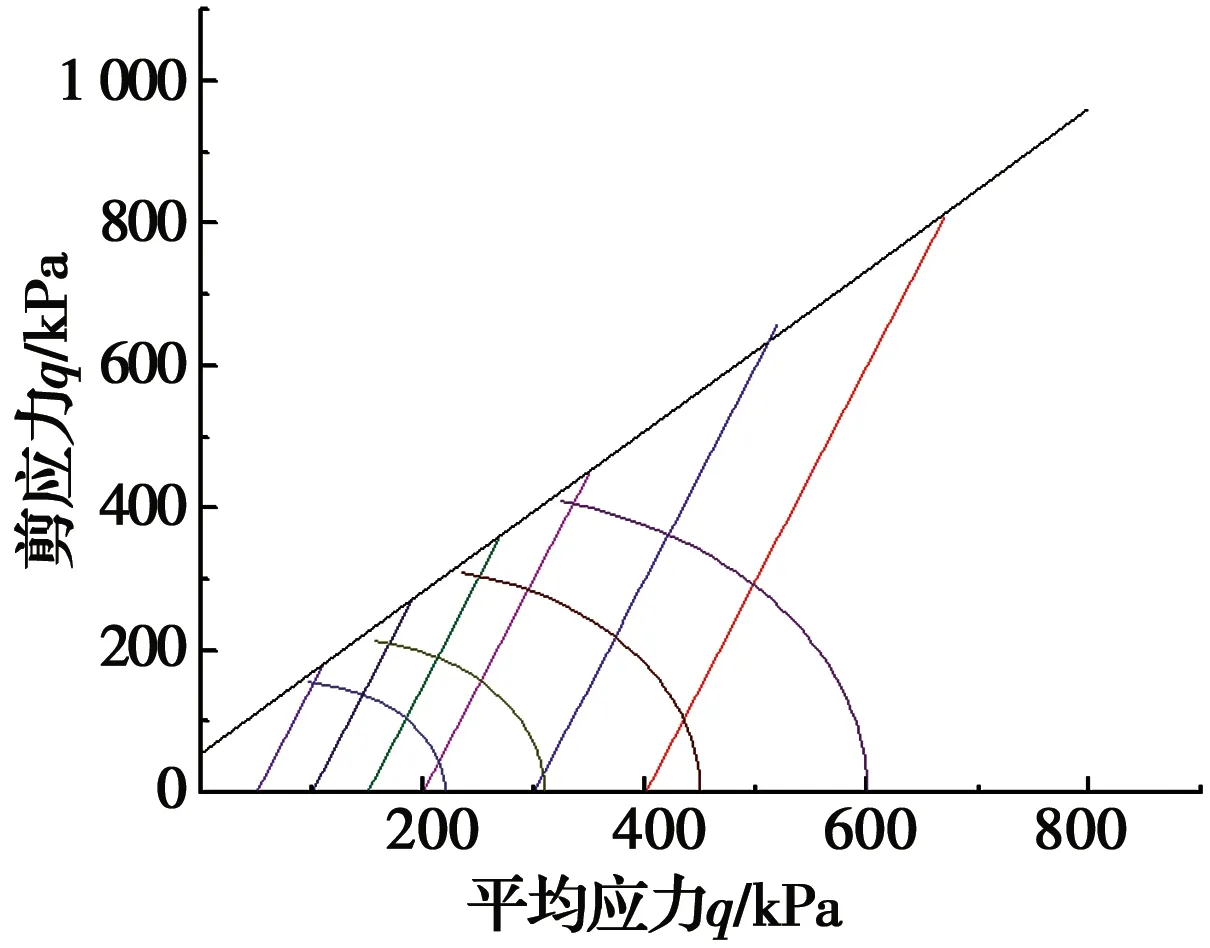
图5 屈服面拟合图Fig.5 Yield surface fitting

2.2 硬化参数的确定

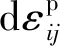
(3)

结合式(2)、式(3)，可得到硬化参数与塑性功的关系，如图6所示。

根据图6的拟合结果，硬化参数曲线可以用驼峰曲线表示，最终表示为

(4)

式中：a、b、c为试验参数，为围压σ3的函数，可以通过驼峰曲线的规律计算得到。试验参数计算式为

(5)

(6)

(7)

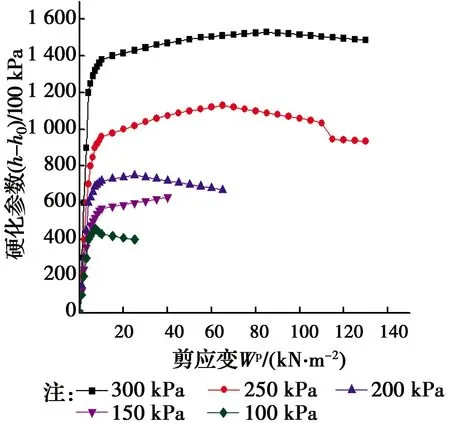
图6 硬化参数h与塑性功Wp关系图Fig.6 Relation diagram of hardening parameter h and plastic work Wp

2.3 验证本构关系

将剪切模量T、体变模量K、屈服曲线f及硬化参数公式h代入普遍的弹塑性增量公式得到p-q坐标系下的本构关系

(8)

式中：D为弹性矩阵；dλ为塑性因子。

模型验证步骤为：1)根据给定的初始应力，计算初始应变；2)根据应力的增量，得到新的应变状态增量；3)根据新的应变增量对应力状态增量进行修正，由此得到新的应变增量；4)如此循环，确定应力-应变关系[20]。对不同条件下试样的应力-应变曲线进行验证，计算曲线与试验曲线结果呈现相似规律。受篇幅限制，只展示自然含水率、150 kPa固结围压的验证结果，如图7所示。

图7 计算与实测应力-应变关系对比图Fig.7 Comparison diagram of calculated and measured stress-strain relationship

由图7可见，该本构关系对变形过程中的弹性部分有较好的契合度，屈服过程也与实际变形基本吻合。但由于黄土土样较大，且内部结构由一定差异，导致在剪切过程中试样表现出的力学性能有些差异[21]。

3 工程应用

3.1 依托工程概况

依托工程为西安到大同高速铁路的某黄土隧道，该隧道位于陕西省合阳县境内，该隧道全长9 359 m，起讫里程DK711+896～DK721+255。隧道开挖宽度为14.9 m，高度为12.7 m，面积153.7 m2，属于大断面隧道，隧道埋深最浅仅15.0 m。地表至90 m深处为Q3粉质粘土。洞口浅埋段为V级围岩，隧道采用三台阶七步法进行开挖施工，支护结构采用复合式衬砌，初期支护采用“型钢钢架+喷射混凝土+钢筋网+锁脚锚管”的型式：27 cm厚C25喷射混凝土；I20a钢架，0.8 m纵向间距；Ф42 mm×4 mm锁脚锚管，长为4.0 m，纵向间距为0.8 m。

建模以里程桩号DK711+910断面根据隧道工程地质情况和当地的降雨强度为例，设置地表渗流量，分析降雨入渗的深度，应用本文建立的本构模型以及调整入渗深度范围内的围岩参数，采用有限元软件Midas进行渗流-应力耦合模拟和分析降雨入渗对黄土浅埋段结构稳定性的影响。

需要说明，在隧道结构设计中初期支护与围岩是主要承载结构，二衬作为安全储备，故数值计算中不考虑二衬结构。为使2D模型有效地反应三台阶施工中的空间效应，结合实际施工情况使用Midas GTS NX 的施工阶段助手功能及荷载生产时步，设置开挖过程释放40%的总荷载，分5次释放，总时长为12 h；初期支护施作过程一次性释放30%的总荷载，总时长为4.8 h；喷射混凝土硬化过程释放30%的总荷载，分5次释放，硬化时长为24 h。另外，试验所得的黄土本构关系已包含着该地区黄土中孔隙和裂隙的影响，对其也不再进行专门的模拟计算。

3.2 建立模型

3.2.1 网格划分 隧道工程实际最浅埋深为15 m，其他3侧边界取至距最大开挖线上圆心70 m处建立2D网格，网格节点共4 884个，单元共4 872个。

3.2.2 边界条件

1)位移约束

模型的左、右边界在X方向固定，底部边界在X和Y方向均不能产生位移。

2)静力荷载约束

隧道埋深为15 m，属浅埋隧道，初始应力场仅考虑自重应力，因此，对模型在Y向施加竖直向下的、大小为1倍自重的约束。

3)渗流边界条件

查阅关中地区的历史气象资料，最大历史24 h降雨量接近于150 mm，故数值计算针对极端降雨情况(大暴雨及以上，24 h降雨量大于100 mm)进行模拟。根据降雨强度，在模型中加载相应的曲面流量，分别为0.13、0.15、0.11 m3/m2/d。

根据室内渗流试验得出，地表黄土的饱和渗透系数为0.851 m/d，地表渗流速度大于降雨速度，因此，本模型的渗流边界条件等于曲面流量。

3.2.3 模型参数

1)支护参数

支护材料与实际工程相同，参数如表3所示。支护结构中喷射混凝土、钢架、锁脚锚管均采用弹性梁单元模拟，仰拱回填混凝土用网格单元模拟。

表3 支护结构力学参数Table 3 Mechanical parameters of support structure

2)围岩参数

渗流分析中需要输入黄土的非饱和参数来计算渗流场，初始渗透系数等参数通过室内试验得到。通过将三轴试验中试样的自然、中值和饱和含水率，可得到水土特征曲线和渗透系数曲线(具体曲线不再列出)。

将得到的本构关系式(8)编译为Fortran语言，再将其导入计算软件的材料属性中的本构关系自定义功能模块。力学参数通过三轴试验数据计算得到，如表4所示。

表4 不同含水率下的围岩力学参数Table 4 Mechanical parameters of surrounding rock under different water content

3.3 模拟结果与分析

3.3.1 降雨影响范围分析 首先，计算不考虑降雨情况下所建模型的含水率整体分布情况，然后，在计算模型自然含水率分布的基础上，考虑降雨强度分别为0.11、0.1和0.15 m/d且降雨历时为1 d时，计算模型含水率分布情况。最上层模型的计算结果如图8所示。

图8 体积含水率分布Fig.8 Volumetric moisture content distribution

由图8可见，自然状态下含水率分布受地下水影响随深度增加而略微增大。考虑不同降雨强度时，随着降雨强度增大，2 m深度内土层会不断接近饱和；超过2 m后，含水率随深度增加而减小；当深度达到5 m左右时，含水率随深度不再增加，但处于非饱和状态。从结果看，计算结果与文献[11]所做的现场试验结果大致相同。取每1 m厚度土层含水率的平均值并近似等效为18%、22%、26%、30%中最接近的值，以此模拟降雨对围岩性质的影响，调整方案如表5所示。

表5 降雨影响后的围岩参数Table 5 The parameter of surrounding rock after the influence of rainfall

注：表中用含水率代替具体的围岩参数，不同含水率的具体参数见表2。

3.3.2 隧道结构稳定性分析 在得到降雨入渗的影响深度后，对正常情况下隧道施工进行模拟。分别对3种降雨情况下隧道施工过程进行分析，得到不同情况下隧道的受力与应变情况，结果如图9～图11所示(受篇幅限制只展示无降雨和最强降雨两种边界条件计算结果)。

图9 围岩竖向位移云图Fig.9 Vertical displacement cloud chart of surrounding rock

图10 隧道喷射混凝土应力Fig.10 Shotcrete stress of the tunnel

由图9可见，围岩的最大竖向位移发生在隧道拱顶上方围岩。不考虑降雨时，拱顶最终沉降为12 cm。考虑降雨入渗后，土体黏聚力降低，导致围岩位移大幅所增加。当降雨强度分别为0.11、0.13和0.15 m/d时，拱顶最大沉降值分别为13.5、14.7和17.5 cm，说明降雨入渗对浅埋大断面黄土隧道沉降的影响非常大，且随着降雨强度的增大而影响增强。

由图10可见，不考虑降雨时，初期支护结构中喷射混凝土结构最大应力为3.77 MPa。当降雨强度为0.11、0.13和0.15 m/d时，喷射混凝土最大应力分别为4.27、4.39和4.77 MPa。喷射混凝土应力相对于不考虑无降雨时增加26%，说明降雨对该隧道初期支护喷射混凝土应力的影响比较明显。

图11 隧道钢架应力Fig.11 Steel frame stress of tunnel

由图11可见，初期支护结构中钢架应力与喷射混凝土应力规律类似，不考虑降雨时，最大应力为34.4 MPa。当降雨强度为0.11、0.13、0.15 m/d时，钢架应力分别为38.9、40.0、43.6 MPa，应力最大值相对于不考虑降雨时增加了27%。降雨对钢架应力的影响依旧明显。

在钢架受弯方面，最大弯矩主要分布在隧道拱腰位置。考虑降雨对钢架受力有明显的变化，不考虑降雨时弯矩最大值为24.9 kN·m。当降雨强度为0.11、0.13和0.15 m/d时，弯矩分别为27.1、28.8和29.9 kN·m，最大值比不考虑降雨时增加20%。

由以上分析可见，虽然降雨入渗深度影响范围仅5 m左右，但因埋深较浅，隧道上部围岩自稳能力受到很大影响，导致地表水入渗对隧道稳定性造成很大影响。主要表现在围岩变形和结构受力增大两个方面：考虑降雨入渗与不考虑降雨时，隧道初期支护结构应力涨幅在20%～27%，而围岩变形涨幅达到了30%。因此，强降雨会对浅埋大断面黄土隧道的稳定性造成很大影响。

3.4 现场测试与验证

为了进一步验证本文提出的黄土弹塑性增量本构关系以及数值模拟结果的准确性，对依托工程隧道断面DK711+910进行变形监测。隧道沉降监测点布设在拱顶，由于隧道采用三台阶七步法开挖，净空收敛分别在上、中、下台阶布设测线，测试方案如图12所示。变形监测共计30 d，其中，晴天10 d，雨天6 d，多云及阴天14 d，最大降雨等级为中雨(10～25 mm/d)。

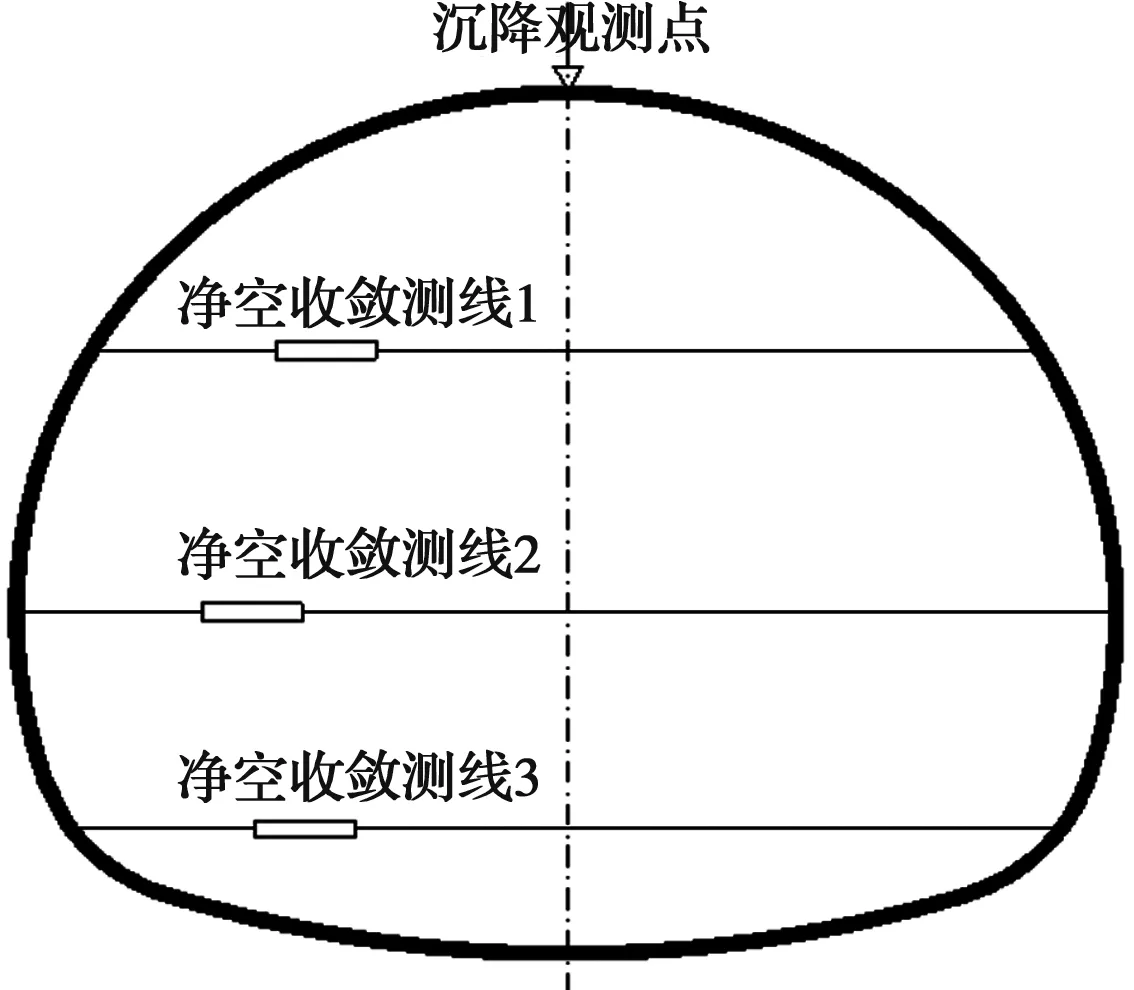
图12 隧道变形测试方案Fig.12 Deformation test scheme of the tunnel

对DK711+910断面变形数值模拟结果与实测拱顶沉降和净空收敛值进行对比分析，并绘制成时态曲线，如图13、图14所示。图13中，分别绘制了降雨强度为0.15、0.13、0.11 m/d，不考虑降雨的数值模拟结果以及实测拱顶沉降时态曲线。图14中，绘制了上述5种工况下，3条测线的净空收敛时态曲线。

图13 拱顶沉降结果对比Fig.13 Comparison of vault settlementvalues

从图13可见，数值模拟的4种工况与实测拱顶沉降的趋势基本一致。考虑降雨时，不同开挖步的拱顶沉降均大于实测值，不考虑降雨时拱顶沉降值为138.0 mm，而实测值为147.8 mm，误差仅为6.7%，实测拱顶最终沉降量与不考虑降雨情况下的数值模拟值比较接近。

图14 净空收敛结果对比Fig.14 Comparison of clearance coverage values

由图14可知，实测3条净空收敛测线的实测值与不考虑降雨情况下的数值模拟结果也比较接近。其中，测线1、2和3实测值分别为62.3、121.5、99.4 mm，与模拟结果的误差分别为9.3%、4.9%和10.9%。总体来看，无论是拱顶沉降，还是净空收敛，实测值与数值模拟值误差均较小。与测试结果的对比表明，本文建立的黄土弹塑性增量本构关系能比较准确地反映不同含水率黄土地层的力学特性，建立的本构关系合理，数值模拟结果与实测误差较小。

4 结论

以某大断面黄土隧道为工程依托，通过室内三轴试验，建立了黄土弹塑性增量本构关系，并将此本构模型应用在隧道稳定性数值模拟中，考虑4种降雨入渗条件对浅埋黄土隧道稳定性进行了分析。主要结论如下：

1)三轴试验中，试样的破坏程度随含水率增加而降低；当含水率不变，围压增大后，压密使试样生成新的次生结构和黏聚力，使剪切破坏更为明显。另外，力学指标均随含水率增大而减小，弹性模量、黏聚力和内摩擦角从自然状态至饱和后分别降低43%、62%和16%。

2)与实测结果的对比表明，建立的本构关系比较合理。新的本构关系中屈服函数采用椭圆函数拟合，由于椭圆函数不可能与实际屈服曲线完全契合，导致应力-应变曲线中塑性变形开始后计算应力均小于实际应力，但整个曲线与实际变形曲线契合效果良好。

3)在依托工程中，随着降雨强度的增加，地表2 m深度内的土层会逐步接近饱和，而2～5 m深度土层虽然含水率增加，但处于非饱和状态。考虑降雨入渗作用时，围岩变形明显增加。其中，考虑最强降雨与不考虑降雨入渗作用时，隧道拱顶沉降值从12 cm增大到17.5 cm，增加46%；隧道初期支护结构中喷射混凝土最大应力值增加26%，钢架应力和弯矩分别增加27%和20%。