基于PCA-PSO-SVM模型的海底多相流管道内腐蚀速率预测

王盼锋，王寿喜，马 钢，全 青

(西安石油大学石油工程学院，陕西 西安 710065)

随着我国海底石油的不断开发，海底管道建设也在不断增长，据能源局数据统计，截止2017年底，目前中国海底管道长度已超过8 000 km，已然成为了海上油气运输的“生命线”[1-2]。一旦海底管道发生失效或者破裂，不仅影响正常作业，更会导致生物多样性被严重破坏，造成极大的经济损失。查阅相关资料发现，海底管道失效事件主要由腐蚀造成，其占总事故数的40%。因此，通过对海底多相流管道内腐蚀速率的预测，可以了解管道内腐蚀情况，为预防海底管道腐蚀提供合理的措施与建议,以减少管道失效事件的发生。

目前，针对管道内腐蚀的预测已有大量的研究，如刘威等[3]根据实际海洋材料，将灰色模型GM(1,1)与神经网络模型相结合对海底管道海水腐蚀进行了预测，但并未将预测结果与实际数据作对比，因此模型的准确性还有待商榷；张国安等[4]通过对油气田中CO2腐蚀速率的3种预测模型即半经验模型、经验模型和机理模型进行了分析，结果表明这三种预测模型均存在不完整性，需要进行深入的探讨；Haque等[5]应用人工神经网络研究了管材的腐蚀疲劳性能；Kamrunnahar等[6]将神经网络作为数据挖掘工具进行腐蚀行为预测，结果表明神经网络存在一些缺点，如缺乏逻辑推理能力；邓志安等[7]、李响等[8]通过建立新的预测模型，对海洋管线腐蚀速率进行了研究，但是该模型只能在影响因素较少的前提下才有较高的预测精度；孙哲[9]通过建立BP神经网络算法对南海某多相流海底管段内腐蚀速率进行了预测，并编制了腐蚀速率预测程序，但是该程序预测误差偏大，预测结果不尽人意；Haque等[10]、Jimēnez-come等[11]、Vapnik[12]、Kaveh等[13]基于支持向量机算法对不同条件(氯离子浓度、酸度和温度)下的不锈钢对氯化钠溶液的耐蚀性进行了分析，并建立了腐蚀点蚀预测模型，结果表明支持向量机算法也仅适用于小样本问题。

综上所述，针对管道内腐蚀速率的预测研究目前均存在一定的缺陷，且针对海底多相流管道的内腐蚀速率预测研究相对较少[14]。面对大数据下人工智能的日益强大，本文提出了一种基于PCA-PSO-SVM组合模型的海底多相流管道内腐蚀速率预测的新方法，该方法采用部分实际管道内腐蚀速率及其相关影响因素数据对模型进行训练学习，对另一部分数据进行预测，并将预测结果与实际管道内腐蚀速率进行对比，以此验证模型的准确性。该研究可为海底多相流管道内腐蚀失效计算方法提供可靠的理论依据，为海底管道完整性风险评价提供科学的指导[15]。

1 海底多相流管道内腐蚀机理及其影响因素

1. 1 海底多相流管道内腐蚀的机理

海底多相流管道内的流动和流态极其复杂，输送介质基本为油、气、水三相介质，与单相流管道内的流动相比，海底多相流管道内经常会出现严重的内腐蚀问题[1,12]。其中,CO2腐蚀(sweet corrosion)是海底多相流管道内腐蚀最为常见的腐蚀机理。深海中CO2遇水会形成碳酸溶液，存在H+，钢制材料遇酸性溶液会发生电化学反应,其反应式如下：

CO2+H2O→H2CO3

(1)

(2)

阳极反应：

Fe-2e-→Fe2+

(3)

阴极反应：

2H++2e-→H2

(4)

总反应：

Fe+H2CO3→FeCO3+H2↑

(5)

从上述反应式可以看出，CO2腐蚀每时每刻都会发生，H+的不断产生也会加剧电化学腐蚀的发生。

1. 2 海底多相流管道内腐蚀的影响因素分析

已有研究表明，影响海底多相流管道内腐蚀的因素主要有温度、pH值、流体流速、压力、CO2分压和持液率等。

(1) 温度：查阅相关文献可以了解到温度在60℃左右时钢管CO2腐蚀动力学有质的飞跃变化：当温度大于60℃时，钢管表面易形成一种腐蚀性的保护膜，阻碍了钢材与介质的反应，从而使钢管内腐蚀速率变得缓慢；而当温度低于60℃以下时，随着温度的升高，由于没有保护膜的存在，钢管内腐蚀速率会明显加快，出现点蚀、坑蚀的程度较为严重，且当温度在60～70℃之间时出现钢管内腐蚀速率峰值。

(2) pH值：CO2在水中形成一种弱酸H2CO3，使得溶液pH值减小，不断出现H+之后会加剧阳极的反应。已有文献研究表明，当pH值处于4～6时，电化学反应会剧烈发生，管道内腐蚀现象严重。

(3) 流体流速：管道内腐蚀速率会因流体流速的增加而变大，这是因为流体流速的增加会加速管道内腐蚀过程的进行，并且当流体流动剧烈时，产生的切向力会破坏钢管表面形成的保护膜，加快Fe的化学反应，导致出现严重的局部腐蚀。

(4) 压力：压力对管道内腐蚀也有较为明显的影响。当压力较大时，管道受到了与腐蚀面相互垂直的应力作用，同时伴随着化学腐蚀，管道内腐蚀速率变大，管道寿命缩短；相反，当压力较小时，管道内产生的应力作用小，管道内腐蚀速率会大大降低

(5) CO2分压：CO2分压与温度类似，当温度低于60℃时，随着CO2分压的增大，管道内腐蚀速率加快；当温度大于60℃时，随着CO2分压的增大，管道内表面形成了腐蚀产物膜，阻碍了腐蚀反应的发生，管道内腐蚀速率变慢。

(6) 持液率：在多相流体系中，持液率对于何时何地发生管道内腐蚀以及腐蚀程度具有重要的作用。在多相流体系中，当液相占比较大时，金属表面易形成水膜，酸性气体较快溶解在液相中，此时会提供一种酸性介质，将有利于管道内腐蚀的发生；当液相占比较小时，钢管的润湿性受阻，水完全从金属表面去除，不易形成腐蚀环境，从而使管道内腐蚀速率明显降低。

通过以上分析可以发现，温度、pH值、流体流速、压力、CO2分压和持液率是海底多相流管道产生内腐蚀的重要影响因素，本研究中将着重考虑这六种因素的影响。

2 研究方法

2.1 PCA算法原理

主成分分析(Principal Factor Analysis,PCA)算法是一种数据压缩和数据降维的分析技术[16-18]。PCA算法通过构造一系列线性组合新变量，并在彼此不相关的前提下反映原始数据的信息，且在不影响预测结果的条件下，对海底多相流管道内腐蚀速率的影响因素进行简化，从而提升预测效率。PCA算法的计算步骤如下：

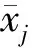
(6)

(2) 建立相关系数矩阵Rm×n。按下式建立相关系数矩阵Rm×n：

(7)

(8)

(3) 计算主成分的贡献率和累计贡献率。依据|R-λE|求解特征根λ1≥λ2≥…≥λm，求出齐次线性方程组(R-λiE)u=0的特征向量u1,u2,…,um，并计算主成分Fi的贡献率ei和累计贡献率P，其计算公式如下：

(9)

(10)

一般情况下，当p个影响因素的累计贡献率超过80%时，就可以使用p个影响因素代替所有的影响因素。在本研究中，为了保障预测结果的准确性，将选择累计贡献率超过90%的影响因素数据代替所有的影响因素数据进行研究。

2.2 PSO和SVM算法原理

2.2.1 粒子群优化(PSO)算法

粒子群优化(Particle Swarm Optimization，PSO)算法是一种通过群体之间相互合作和信息共享，利用迭代方法寻求最优值的优化算法，它是最为常见的寻优算法模型[19-21]。

PSO算法假定每个寻优问题均为在搜索空间的粒子，其主要是通过速度、位置和适应度三个变量表示其特征的。假设搜索空间是N维，群体中有M个粒子，第i个粒子表示一个N维向量，在寻优搜索过程中，每个粒子通过不断跟踪两个最优解(一个是自身最优解Pbesti,另一个是全局最优解Gbestg)进行更新，其关系式如下：

(11)

(12)

2.2.2 支持向量机(SVM)算法

支持向量机(Support Vector Machine，SVM)算法对于解决小样本、非线性和高维模式识别具有明显的优越性，是一种具有良好性能的分类算法，并且其还能推广应用到人工智能、机器学习方面[22]。

SVM算法首先给定样本数据集D={(xi,yi)|i=1,2,…,l},其中xi∈Rn，yi∈R。SVM算法数据预测模型通过引进松弛变量约束η和η*，并且引进从输入空间Rn到Hibbert空间H的变换φ，将数据集D(xi,yi)(i=1,2,…,l,xi∈Rn,yi∈R)映射为f(φ(xi),yi,b)=0(i=1,2,…,l)，将原始的回归问题转化为优化函数问题,如下式：

(13)

式中：ω为权重向量；C为惩罚因子，且C>0。

优化函数的约束条件为

ωT=φ(xi)+b-yi≤ε+ηi

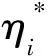
(14)

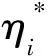
式中：ε为损失函数，且ε>0；b为映射的参数。

若对应的变换φ的核函数为K(xi,xj)，上述问题则转化为

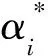
(15)

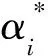
式中：α为拉格朗日乘子。

最终得到优化后的回归函数为

(16)

其中,SVM算法回归的核函数K(xi,xj)主要包括以下几种(可取任意值)：

多项式核函数为

K(xi,xj)=(γxixj+fcoe)d

(17)

径向基核函数为

K(xi,xj)=exp(-γ|xi-xj|2)

(18)

Sigmoid核函数为

K(xi,xj)=tanh(γxixj+fcoe)

(19)

式中：d为幂参数。

在上述三种核函数中，径向基核函数的应用相对较广，因此本研究将选择径向基核函数作为SVM算法的核函数。

2.3 PCA-PSO-SVM组合预测模型

在PCA-SVM预测模型中，先输入温度、pH值、流体流速、压力、CO2分压、持液率6项影响因素，经过PCA算法处理后得到SVM模型预测的主要因素PC1,PC2,…,PCm；然后将海底多相流管道内腐蚀速率的主要影响因素数据和部分管道内腐蚀速率数据作为PSO-SVM预测模型的输入数据，对剩余部分的管道内腐蚀速率进行预测。PCA-PSO-SVM组合模型对海底多相流管道内腐蚀速率进行预测的流程见图1。

图1 PCA-PSO-SVM组合模型对海底多相流管道内腐蚀 速率的预测流程Fig.1 Flow chart of prediction of internal corrosion rate of submarine multiphase flow pipelines based on PCA-PSO-SVM prediction model

3 预测过程与分析

3. 1 数据来源

本研究对我国某海域4条海底多相流管道进行了内腐蚀检测[7]，并对4条海底管道54个位置点的内腐蚀速率进行了计算，同时通过实时仿真设备对4条管道54个位置点处的温度、pH值、流体流速、压力、CO2分压、持液率6项影响因素数据进行了模拟仿真，得到某海域海底多相流管道这些位置点处的内腐蚀速率及其影响因素数据，部分数据见表1。将某海域海底多相流管道这54个位置点的数据分为集合，分别为学习数据集和预测数据集，其中学习数据集包含海底管道44个位置点的数据，用于模型训练；预测数据集包含海底管道10个位置点的数据，用于模型预测和模型误差检验。

表1 某海域海底多相流管道部分位置点的内腐蚀速率及其影响因素数据

3.2 PCA算法预测结果

根据上述的PCA算法原理，使用MATLAB编程软件，依据对某海域海底多相流管道内腐蚀影响因素的分析结果，将温度、pH值、流体流速、压力、CO2分压和持液率输入至PCA算法中，并按照公式(6)至(10)计算，得到PCA算法的处理结果，见表2。

表2 PCA算法的处理结果

由表2可知，温度对于该海域海底管道内腐蚀速率的影响相对较大，这与文献中的分析结果一致，而压力对该海域海底管道内腐蚀速率的影响相对较小。通过本研究可以发现，温度、pH值、流体流速、CO2分压和持液率这五项影响因素对海底多相流管道内腐蚀速率的累计贡献率已经超过了90%，因此为了减少模型的数据训练与预测时间，可以忽略压力对海底多相流管道内腐蚀速率的影响，只将温度、pH值、流体流速、CO2分压和持液率这五项影响因素作为海底多相流管道内腐蚀速率的影响因素展开下一步的研究。

3.3 PSO算法寻优结果

在使用PSO算法对参数进行寻优的过程中，搜索空间的维度N设置为2，权重因子ω设置为2,加速度因子c1和c2分别设置为0.9和0.4，为了得到最优的参数，寻优过程中的迭代次数设置为1 000次，通过使用MATLAB编写PSO算法对SVM算法中的参数C和ε进行寻优。

除PSO算法以外，常见的SVM算法参数寻优主要有三种，分别是遗传算法(GA算法)、最小二乘算法(LS算法)和交叉验证算法(CV算法)，本文分别使用这三种寻优算法对SVM算法公式(13)、(14)中的参数C和ε进行优选，寻优计算结果见表3。

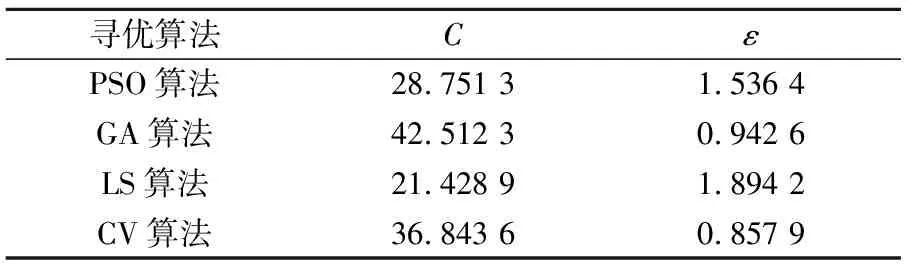
表3 不同算法对参数C和ε的优选结果

3.4 PCA-PSO-SVM组合模型的预测结果分析

只从寻优的结果角度出发，无法检验PCA-PSO-SVM组合模型的优越性，因此需要将PCA-PSO-SVM模型与PCA-GA-SVM模型、PCA-LS-SVM模型和PCA-CV-SVM模型预测的误差进行对比。

根据PCA算法影响因素分析结果和PSO算法参数寻优结果，在MATLAB软件中建立SVM模型，依据SVM算法原理和公式(13)～(16)，将温度、pH值、流体流速、CO2分压和持液率这五项影响因素作为海底多相流管道内腐蚀速率的影响因素，使用某海域海底管道44个位置点的数据对PCA-PSO-SVM组合预测模型进行训练，并对剩余的管道10个位置点的内腐蚀速率进行了预测，计算每个位置点处的预测误差和所有预测结果的平均绝对误差，同时将该组合预测模型与PCA-GA-SVM模型、PCA-LS-SVM模型、PCA-CV-SVM模型的预测结果进行了对比。在应用这些算法的过程中，输入数据的维度为6维，输出数据的维度为1维，SVM算法中核函数选择径向基核函数，参数C和ε的选择来源于表3，通过MATLAB程序分别进行预测，最终得到不同预测模型的预测结果见图2，不同预测模型的绝对误差变化见图3，不同预测模型的平均相对误差以及模型训练所需要的时间见表4。

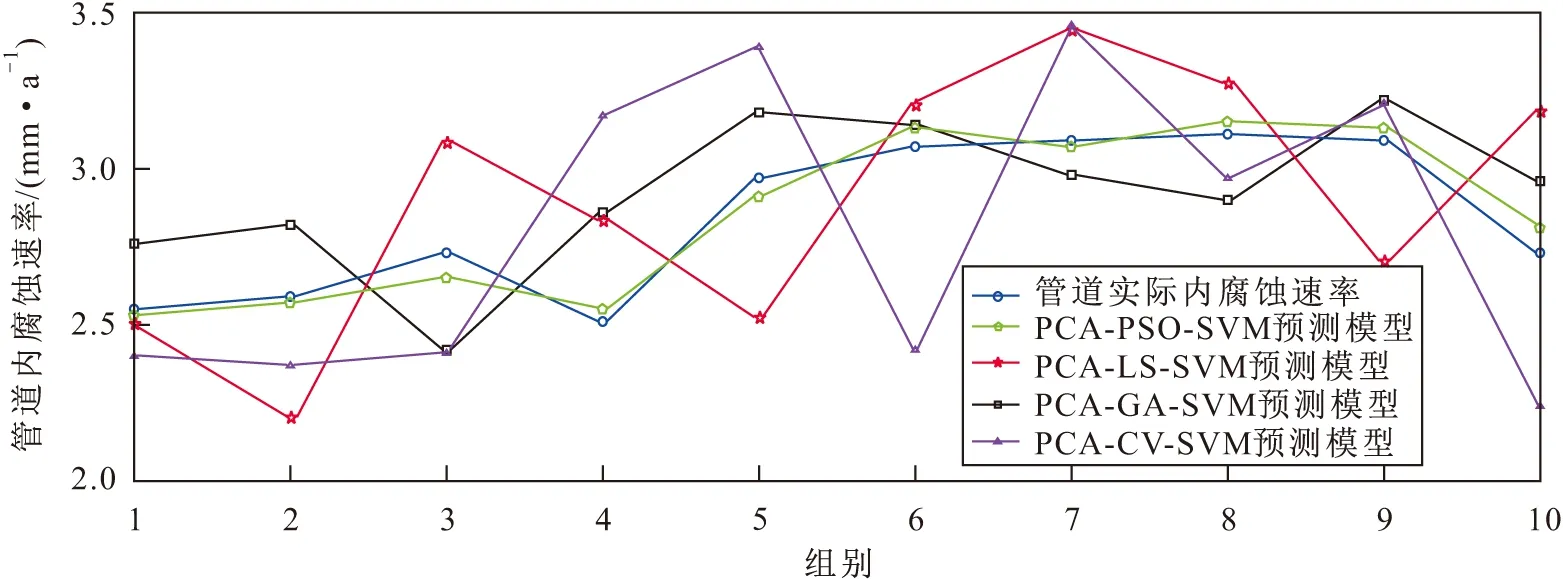
图2 不同预测模型的预测结果对比Fig.2 Comparison of prediction results of different models

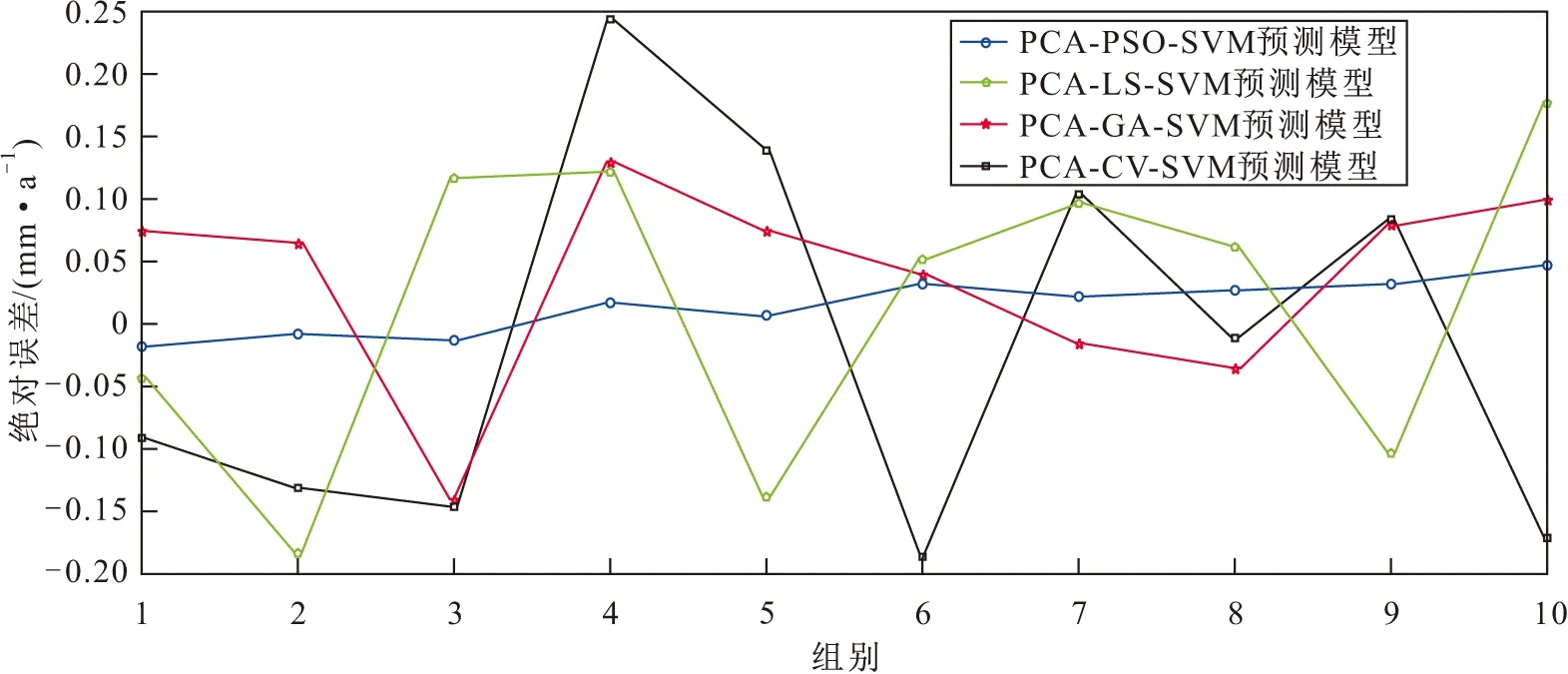
图3 不同预测模型的绝对误差对比Fig.3 Comparison of absolute errors of different models

表4 不同预测模型的平均相对误差和模型训练时间

由图2、图3和表4可以看出：PCA-PSO-SVM组合模型预测结果的变化趋势与管道实际内腐蚀速率变化趋势基本一致，管道10个位置点内腐蚀速率的预测相对误差均没有超过5%，且与其他3种预测模型相比，该组合预测模型的平均相对误差仅有1.848%，远低于其他预测模型；在模型训练时间方面，组合预测模型仅需要3.17 s，也小于其他3种预测模型的学习时间。因此，针对海底多相流管道内腐蚀速率的预测问题，本文所提出的PCA-PSO-SVM组合预测模型具有可靠性和可行性。

4 结 论

本文对海底多相流管道内腐蚀速率的影响因素进行分析，对PCA算法、PSO算法和SVM算法进行了理论介绍，并提出了可用于海底多相流管道内腐蚀速率预测的PCA-PSO-SVM组合模型。该组合模型先使用PCA算法对海底多相流管道内腐蚀速率的影响因素进行降维，再使用PSO算法对SVM算法的参数进行寻优，并在此基础上使用SVM算法对44组海底多相流管道内腐蚀的影响因素数据和管道内腐蚀速率数据进行学习训练，对10组海底多相流管道内腐蚀速率数据进行预测，同时计算该组合模型预测的平均相对误差和模型训练时间，将其与其他预测模型进行了对比，以验证模型的可靠性。通过本次研究可以得出以下结论：

(1) 海底多相流管道内腐蚀速率受温度、pH值、流体流速、压力、CO2分压和持液率6项因素的影响，其中温度对海底多相流管道内腐蚀的影响相对较大，压力对其影响相对较小，因此为了简化模型、缩短高模型训练时间，可以忽略压力对海底多相流管道内腐蚀的影响。

(2) 使用PCA-PSO-SVM组合模型对海底多相流管道内腐蚀速率进行预测时，该组合模型的相对误差最大不超过5%，平均相对误差仅有1.848%，而在模型训练时间方面，该组合预测模型仅需要3.17 s，这两项数据均小于其他预测模型，表明针对海底多相流管道内腐蚀速率的预测问题，PCA-PSO-SVM组合预测模型具有可靠性和可行性。