基于人工神经网络的炭质岩隧道锚杆应力计算研究

2020-05-21王才进骆俊晖段隆臣

安全与环境工程 2020年2期

王才进，骆俊晖，张涛，段隆臣，马冲

(1.中国地质大学(武汉)工程学院，湖北武汉 430074；2.广西交通设计集团有限公司，广西南宁 530029；3.中国地质大学(武汉)数学与物理学院，湖北武汉 430074)

锚杆支护的使用始于20世纪初期，自德国谢列兹矿最先采用锚杆支护井下巷道以来，锚杆支护以其结构简单、施工方便、成本低和对工程适应性强等特点，在土木工程(包括采矿工程)中得到了广泛的应用。随着全长黏结式锚杆的使用，锚杆在软弱围岩隧道加固中也得到了推广，特别是“新奥法”的成功，进一步确定了锚杆在软弱围岩隧道支护结构中的作用[1-3]。

近年来，研究人员对隧道锚杆支护受力机制进行了大量的研究。如王明恕等[4]根据全长锚固锚杆的作用机理，提出了锚杆的中性点理论；Li等[5]建立了岩石锚杆拉拔试验承受拉力的分析模型，认为锚杆受力是一种叠加力；郭小红等[6]根据锚杆承载拱理论给出了计算系统锚杆承载力的计算方法；文竞舟等[7]通过求解锚杆轴向位移的微分方程，并经过算例分析得出适当增加全长黏结式锚杆的锚固长度能有效改善锚杆的锚固效果。上述关于隧道锚杆应力的计算主要是在理论分析的基础上进行的，但值得注意的是，影响锚杆应力的因素很多，如锚杆的类型、锚固岩土体性质和施工工艺等，这些因素都会影响锚杆的锚固效果，而这些因素难以在现有的理论计算中得到全面考虑，并且理论方法具有地域性限制，所得结果与实际值偏离较大，难以在工程设计中推广应用。因此，本文以某炭质岩隧道锚杆加固为工程背景，根据工程地质条件与现场实际监测情况，采用人工神经网络分析方法，分析了围岩应力、渗透压和围岩应变对隧道锚杆应力的影响，建立了可估算隧道锚杆应力的人工神经网络模型，并通过将模型预测结果与实测结果进行比较，以验证模型预测隧道锚杆应力的准确性和有效性，为隧道设计提供参考。

1 工程概况

以广西河池至百色高速公路岜向隧道为依托，选择Ⅳ级围岩段和Ⅴ级围岩段进行锚杆轴向应力现场测试，现场测试段为炭质岩隧道。

岜向隧道为分离式长隧道，走向约为246°，隧道左线设计长度为1 815.0 m，进、出口隧道路面设计高程分别为387.959 m、432.114 m，最大埋深约为245.99 m；隧道右线设计长度为1 850.0 m，隧道进、出口路面设计高程分别为387.941 m、432.488 m，最大埋深约为226.03 m。根据钻孔及工程地质测绘资料，隧道区地层由新到老主要由第四系冲洪积层(Qal+pl)、第四系残坡积层(Qel+dl)、石炭系下统大塘阶(C1d)、石炭系下统岩关阶(C1y)、泥盆系上统同车江组(D3t)、泥盆系上统榴江组(D3l)地层和断层破碎带组成。

现场试验段选择在该隧道Z2K4+120～Z2K4+520段，该试验段是炭质岩围岩等级最高的断面，监测断面埋深约为92 m，属泥盆系上统同车江组(D3t)地层，其岩性为薄—中层状泥页岩、炭质泥岩、泥质粉砂岩夹硅质岩，受褶皱挤压的影响，岩石碎裂化及硅化较严重，岩体破碎，呈碎裂状结构，围岩稳定性较差。隧道施工采用台阶开挖方法，最大开挖跨度为12.2 m，该隧道现场施工情况见图1。

图1 某炭质岩隧道现场施工情况Fig.1 Construction conditions of a carbonaceous tunnel in the field

某炭质岩隧道监测点初期支护由喷射混凝土、钢筋网和锚杆组成；锚杆为φ25 mm、长4 m，间距为1.2 m×0.5 m；初期支护采用C25的喷射混凝土，二次衬砌采用C25整体式现浇混凝土。某炭质岩隧道监测断面的复合衬砌结构设计图，见图2。

图2 某炭质岩隧道监测断面的复合衬砌结构设计图(单位：cm)Fig.2 Composite lining structure design of the monitoring section of a carbonaceous tunnel (unit:cm)

2 隧道锚杆布置及锚杆应力现场测试

锚杆应力测量采用GJ-16振弦式钢筋测力计(见图3)，该测力计由振弦式钢筋应力计和测量线组成，测量线末端与频率仪相连，根据隧道监测点的钢筋应力计中钢弦的频率变化，进而得出锚杆的应变和应力。

图3 振弦式钢筋测力计Fig.3 Vibrating wire type dynamometer

本次现场试验在某炭质岩隧道左线围岩等级最高的地方选取3个监测断面(A、B、C)，在完成二次衬砌施工后开始锚杆应力测量，其中监测断面A和B(Z2K4+140、Z2K4+155)在Ⅴ级围岩段，监测断面C(Z2K4+170)在Ⅳ级围岩段；GJ-16振弦式钢筋测力计设置在锚杆的中部，锚杆及监测点的布置图见图4；每个监测断面设置4个监测点(M1、M2、M3和M4)，其中M1、M2、M3和M4监测点分别在锚杆左拱脚、右拱脚、左拱肩和右拱肩。监测点位置同时布置土压力盒、渗压计和应变计，用来监测该处的围岩应力、渗透压和围岩应变位移。

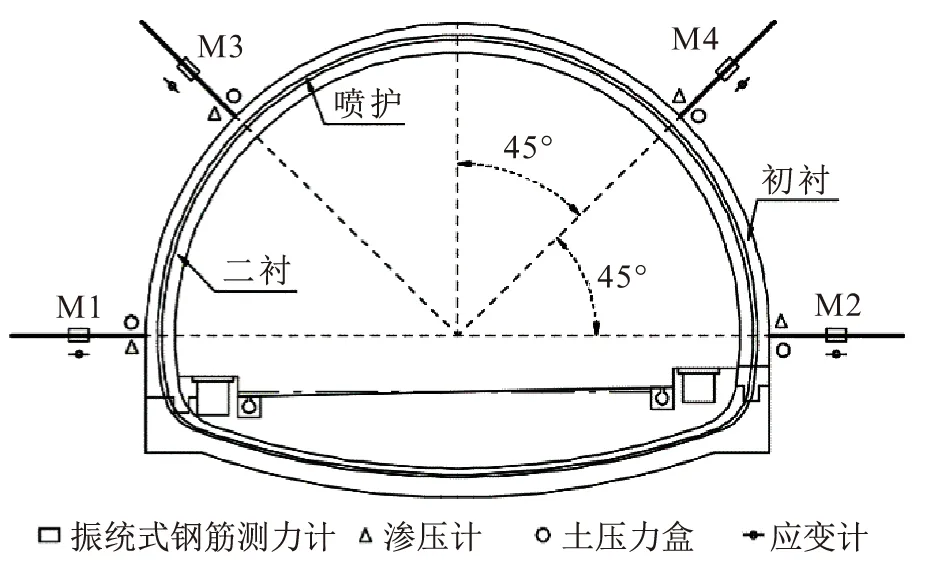
图4 某炭质岩隧道锚杆及监测点的布置图Fig.4 Layout of the bolt and monitoring points of a carbonaceous tunnel

某炭质岩隧道现场试验监测断面A、B和C各监测点的锚杆应力时程曲线，见图5。

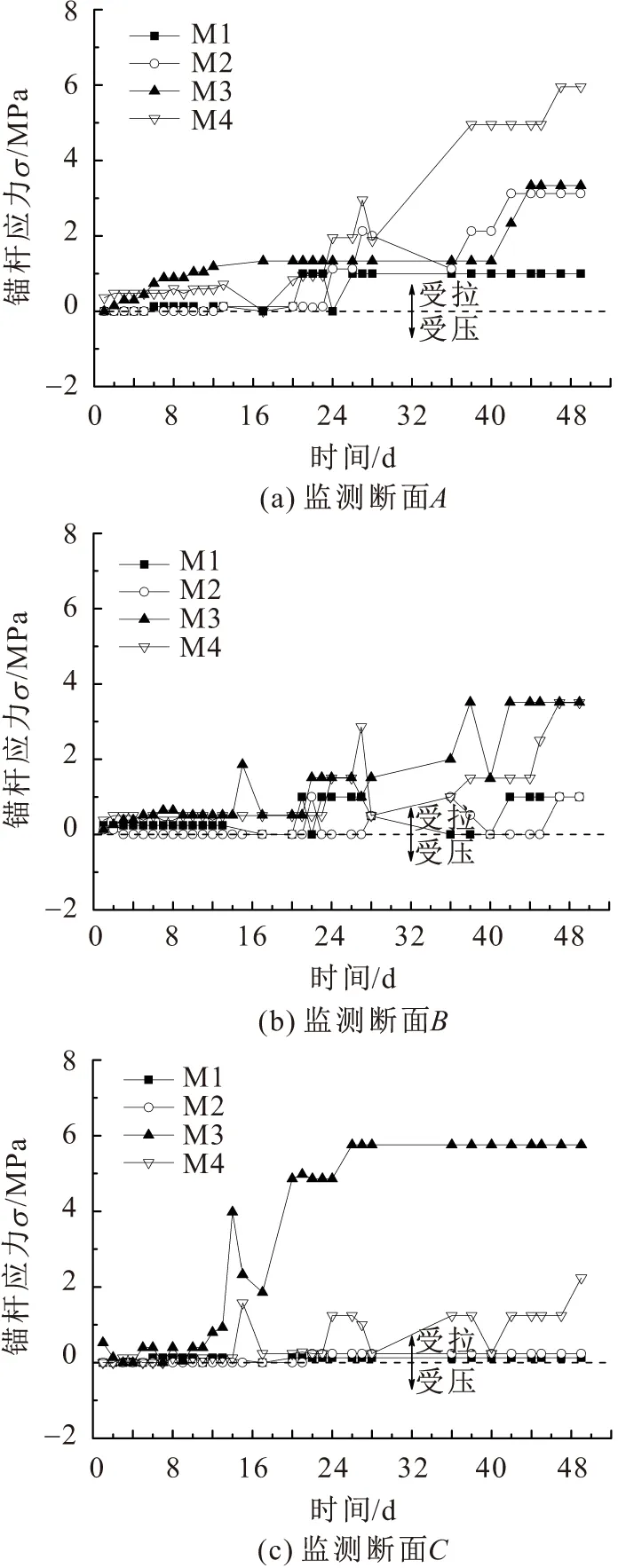
图5 某炭质岩隧道现场试验监测断面A、B、C各监测点的锚杆应力时程曲线Fig.5 Time history curves of bolt stress at monitoring points on the monitoring sections A,B,C in field test of a carbonaceous tunnel

由图5可见：该隧道3个监测断面锚杆主要承受拉力，锚杆在拱肩处受到的压力大于拱脚处；拱肩处的锚杆应力随着时间的增加而缓慢增加，监测一段时间后增加加快，最后达到最大值；拱脚处的锚杆应力监测一段时间后才从零开始增加，最后的增加量很小，而监测断面C拱脚处的锚杆应力为零；在监测到14～18 d、24～28 d和36～40 d时该锚杆应力时程曲线波动较大，这是由于监测期间有几次暴雨，炭质页岩遇到雨水软化造成的。

3 基于人工神经网络的隧道锚杆应力预测

3. 1 人工神经网络分析方法

人工神经网络(Artificial Neural Network,ANN)是由相互连接的神经元组成的复杂网络，该网络试图模仿人类大脑和神经系统的行为，是一种人工智能。神经元在逻辑上按层排列：输入层、一个或多个隐藏层和输出层。神经元通过加权连接相互作用，每个神经元都连接到下一层的所有神经元。输入层是将数据呈现给网络的方式，输出层保持网络对输入的响应。目前，没有分析方法将网络结构定义为问题复杂性的函数，必须反复试验手动选择结构，一个或两个隐藏层对于大多数问题是非常有效的[8-11]，隐藏层使网络能够表示输入层与输出层之间的复杂关联，该神经网络结构被称为完全互连的前馈多层神经网络(MLP)。图6为人工神经网络(ANN)结构，其中P1、P2和P3作为输入层，H1和H2作为隐藏层神经元，R1、R2和R3作为输出层。

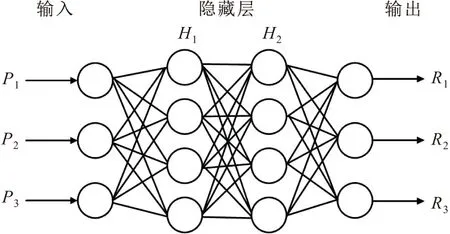
图6 人工神经网络(ANN)结构Fig.6 Structure of the Artificial Neural Network(ANN)

目前逆向传播神经网络在岩土工程和地质工程领域得到了很好的应用[12-15]。逆向传播神经网络通过将隐藏层的神经元权重相乘，再对乘积进行求和，然后使用非线性传递函数来得到输出层。在岩土工程领域，常用到的神经网络传递函数是sigmoid函数。ANN通过比较输出值与实测值的误差进而修改隐藏层神经元的权重来“学习”，误差项导数的负值与权重的变化呈比例关系。通过训练，直到输出值与实测值的均方误差最小且小于指定的误差时停止训练。根据相关系数R2、均方根误差RMSE和方差比VAF等值的大小可以评估ANN模型的性能[16-19]。当R2的值接近1且误差项的值很小则ANN模型训练有素。

本文利用ANN技术建立估算隧道锚杆应力的计算模型，预测锚杆的应力，其中训练是在Matlab的神经网络工具箱中完成，选择Levenberg-Marquardt反向传播学习算法用于训练过程。

3. 2 人工神经网络模型的建立

根据现场试验的数据，分别对隧道监测断面A(命名为ANN-A)、B(ANN-B)和C(ANN-C)建立ANN模型用来预测隧道锚杆的应力值。ANN模型有3个输入参数，即渗透压Π、围岩应力σ1和围岩变形位移D，模型的3个输出参数均为锚杆应力σ。本文选择这3个参数作为模型的输入参数是因为这些参数是影响锚杆受力的主要因素，其中渗透压Π和围岩应力σ1是影响锚杆受力的主要因素，围岩变形位移D是影响锚杆变形的主要因素。

表1分别列出了ANN模型的输入和输出参数的边界值。将每个ANN模型的输入、输出参数数据在0和1之间进行归一化处理。

表1 单个人工神经网络模型输入和输出参数的边界值

在构建模型过程中，通常将试验数据分成两个数据集，一个数据集用于神经网络训练来构建ANN模型，另一个独立的数据集用来估计ANN模型的性能[20]。但将试验数据分成两个数据集用于神经网络训练可能会出现过度拟合的情况，使ANN模型不能很好地推广到新数据[18]。因此，本文使用交叉验证技术来作为神经网络训练终止的标准[21]。在交叉验证中，将数据库分为训练集、验证集和测试集三个子集。其中，训练集用于更新神经元的权重，同时监测设定的误差；当验证集误差开始增加时，由于它被认为是最佳的泛化点，所以停止模型训练；最后，将测试集数据馈送到ANN模型以评估其性能。本文将55%的监测数据用于模型训练，25%的监测数据用于单个模型的验证，20%的监测数据用于模型测试。

Matlab神经网络工具箱是一种流行的数值计算和可视化软件[18]，可用于多层感知器的训练和测试。在模型测试中，首先选择1个隐藏层，隐藏层的神经元数量从1开始增加；然后选择2个隐藏层，隐藏层的神经元数量从1开始增加，通过训练得出最佳隐藏层数和隐藏层神经元数。传递函数采用Log-sigmoid和Tan-sigmoid，以使ANN模型在训练和测试中达到最佳性能。在模型训练中，选择不同的动量因子μ如0.001、0.002和0.003作为训练过程，以寻找最有效的ANN结构；选择最大训练时期数为1 000次，采用相关系数R2和均方误差(MSE)来评估ANN模型的性能，当MSE值最小和R2值最大时为最佳ANN结构。Sigmoid函数的表达式和均方误差(MSE)的计算公式如下：

(1)

(2)

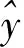
表2给出了性能最佳的单个人工神经网络模型的计算参数信息。

单个人工神经网络模型(训练集、验证集和测试集)锚杆应力的预测结果与实测结果的比较，见图7。

表2 性能最佳的单个人工神经网络模型的计算参数

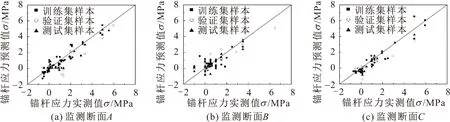
图7 单个人工神经网络模型锚杆应力预测值与实测值的对比Fig.7 Comparison of bolt stress between predicted values by individual ANN models and measured values

由图7可见，人工神经网络模型预测得到的锚杆应力值与实测值基本一致，且模型预测精度较高，这表明人工神经网络模型能够准确、有效地预测锚杆应力。

表3给出了人工神经网络模型的输入、输出参数权重值和偏差值。

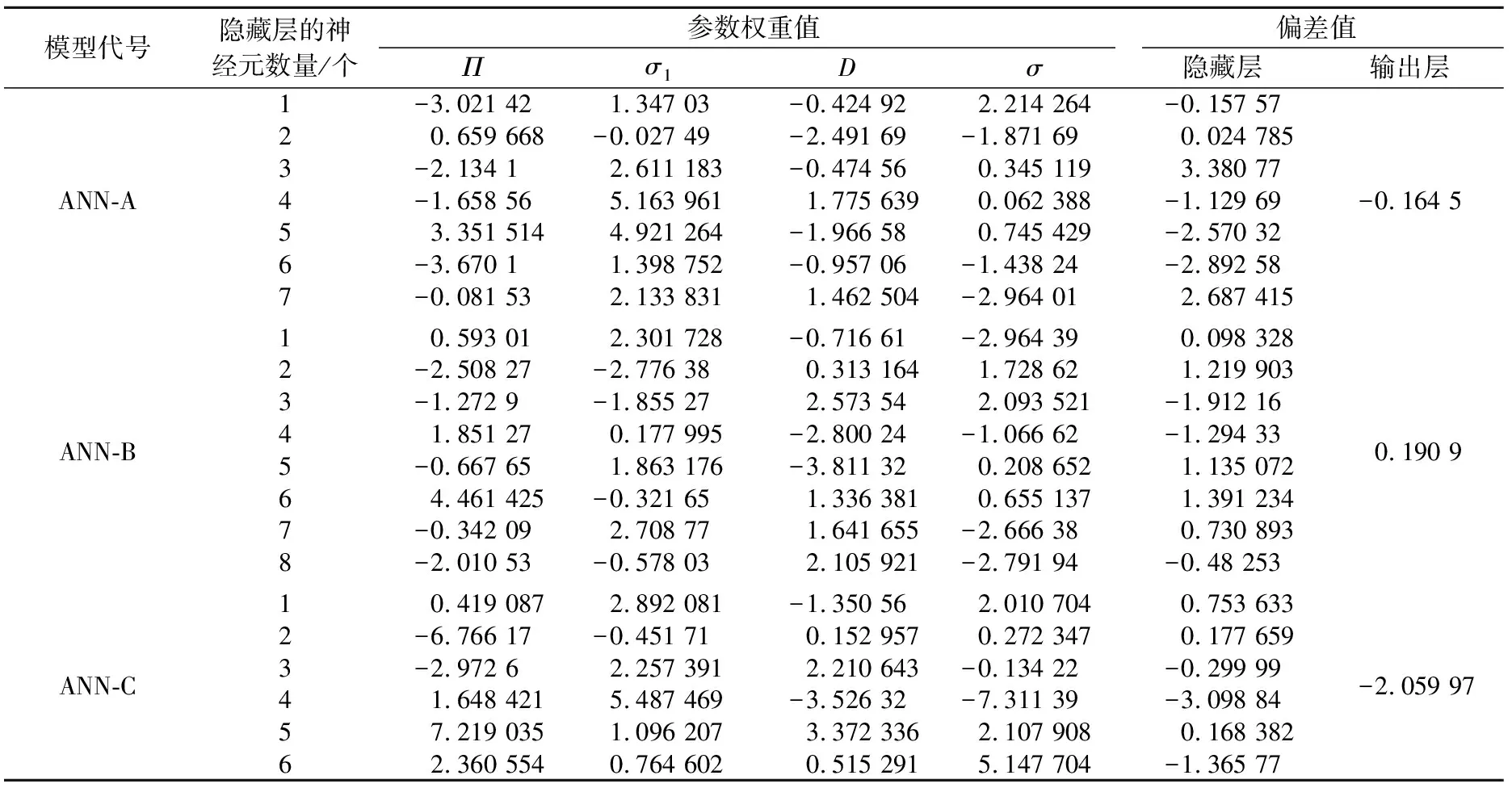
表3 单个人工神经网络模型的输入、输出参数权重值和偏差值

3. 3 人工神经网络模型的性能检验

实际上，预测值与实测值之间的相关系数是检验ANN模型预测性能的一个重要指标。在本文中，还将方差比(VAF)和均方根误差(RMSE)用于检验ANN模型的性能。方差比(VAF)和均方根误差(RMSE)的计算公式如下：

(3)

(4)

如果VAF为100%且RMSE为0，则表示该ANN模型的性能最佳。

表4列出了单个人工神经网络模型的性能检验指标值。

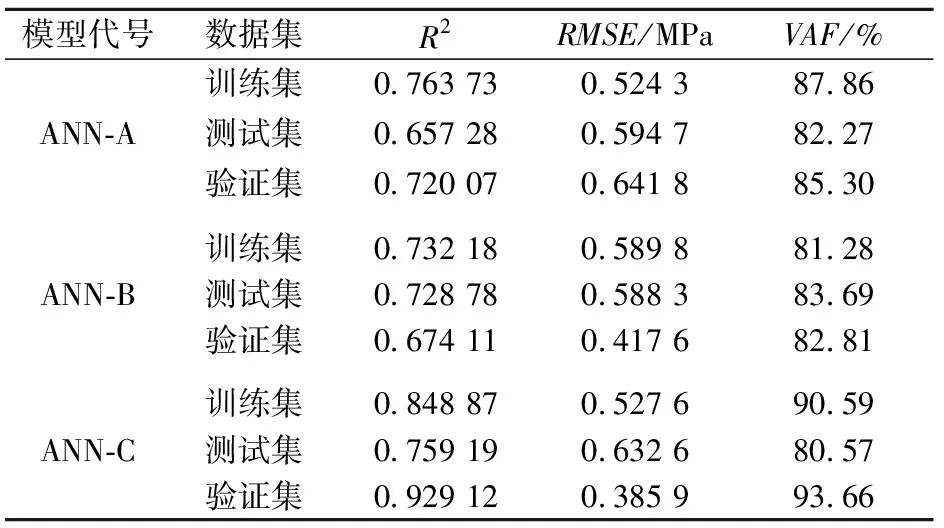
表4 单个人工神经网络模型的性能检验指标值

由表4可见，不同ANN模型的相关系数R2均大于0.65，均方根误差RMSE均小于0.65 MPa，方差比VAF均大于80%，表明建立的ANN模型在预测锚杆应力方面非常有效。

单个人工神经网络模型锚杆应力的预测值与实测值的比较，见图8。

图8 单个人工神经网络模型锚杆应力预测值与实测值的比较Fig.8 Comparison of bolt stress between predicted values obtained from individual ANN models and measured values

由图8可见，该隧道监测断面A的相关系数R2为0.720 1，监测断面B的相关系数R2为0.674 1，监测断面C的相关系数R2为0.929 1；其中监测断面A和监测断面B的相关系数R2低于监测断面C，这是因为监测断面A和监测断面B的围岩等级为Ⅴ级，而监测断面C的围岩等级为Ⅳ级，围岩等级越高围岩越不稳定，影响锚杆应力的因素也会发生相应的改变，所以监测断面A和监测断面B的相关系数R2低于监测断面C，但从预测结果来看，每个人工神经网络模型都能够准确地预测锚杆的应力值。