基于孔洞填充的残缺三维模型检索

陈思琦，刘 丽，陈秀秀，张 龙，王天时

山东师范大学 信息科学与工程学院，济南 250014

1 引言

随着信息技术的不断发展和人们生活水平的提高，人们对色彩、视觉享受的要求越来越高，单一的图像、文本、音频等已经远不能满足人们的需求。因此，三维模型应运而生，凭借其丰富的形状信息和逼真的视觉效果，广泛应用于三维游戏、虚拟现实环境、计算机辅助设计、考古学[1-6]等多个领域。

在众多三维模型中，至少有10%～20%的三维模型存在残缺或信息不完整，其中包括年代久远的出土文物的自然破损、外力造成的人为缺损和扫描时因遮挡或其他原因造成的三维模型信息不完整等。信息缺失的三维模型无法表达完整的模型信息，对残缺三维模型特征的提取也会受到残缺区域的影响。因此，在三维模型检索时，残缺区域较大的残缺三维模型也难以得到理想的检索结果。

在众多三维模型检索方法中，主要有两大类方法：基于视图的方法和基于投影的方法[7]。Ansary等[8]提出自适应视图聚类算法（Adaptive Views Clustering，AVC），利用两个单位正二十面体得到三维模型的320张投影，选取代表性图像，引入一种概率统计方法来计算两个三维模型的相似距离；Papadakis等[9]提出全景视图三维模型检索算法，将三维模型分别进行复数主成分分析（Complex Principal Component Analysis，CPCA）、法向主成分分析（Normal Principal Component Analysis，NPCA）后，放入圆柱体内沿三个坐标轴进行放射投影，得到灰度图后，分别提取Fourier 特征和离散小波变换（Discrete Wavelet Transformation，DWT）特征，并以此来计算两个三维模型的相似距离。此类方法通过投影获得三维模型的二维信息，但是没有充分学习视图间关系，检索精确度有待进一步提高。Gao等[10]提出一种与相机位置无关的三维模型检索算法，将视图集聚类后，引入高斯模型来进行模型间匹配。此类方法通过学习视图间关系，提高了检索精确度，但是其特征描述符表达能力不足，限制了精确度的进一步提升。Gao 等[11]将词袋模型引入三维模型检索，提高了检索效率；Zhao等[12]利用多特征融合的方式，对三维模型进行检索；Nie等[13]将稀疏编码引入三维模型检索，取得了较好的检索精确度。此类方法直接以三维模型的多视图作为算法输入，复杂性相对较低，检索结果优异，但是没有充分考虑视图间关联。

虽然三维模型检索方法较多，各自有其优点，但这些方法都难以有效实现对残缺模型的检索。因此，本文以残缺三维模型为研究对象，通过填充残缺三维模型建立其与对应的完整三维模型之间的形状关联，从而实现残缺三维模型的有效检索。

2 基于孔洞填充的残缺三维模型检索

若想将残缺三维模型填充成为完整三维模型，首先要确定残缺三维模型的孔洞边界，使用填充算法进行填充，但在填充时需要注意的是，填充后孔洞区域应与模型其他区域平滑自然地衔接；填充完成后，对于填充三维模型的每一点，取与该点距离最近的n个点构建矩阵，通过求解矩阵获得该点的曲率值，作为填充三维模型的特征；最后，对填充三维模型使用聚类算法进行聚类，并计算填充三维模型与不同三维模型之间的曲率差值，从而获得两个三维模型的相似距离。

2.1 高精度的孔洞填充

孔洞填充属于无中生有的过程，填充数据与原数据之间存在一定误差，因此，需要不断优化填充后的数据，以达到填充数据与原数据误差尽可能小的目的。

三角网格模型由一系列三角面片组成，通常情况下，每条边连接两个三角面片。假设三角网格模型的曲面为M，对M上所有的边进行检测，若M上某条边只连接了一个三角面片，则这条边即为孔洞区域的边界边。所有只连接一个三角面片的边最后连接包围的区域即为孔洞区域，这些边即为孔洞区域的边界。

确定边界后，采用最小角度法对网格进行初始化填充，首先计算边界边长度的平均值ˉ；再计算每条边界边与其相邻边的夹角大小，并找出具有最小夹角的边界点，计算它的两个相邻边界点的距离d，若d ＜2×，则增加一个三角形，反之则增加两个三角形；最后，更新边界点的信息，判断孔洞是否填充完成。

使用最小角度法填充的网格效果并不是很好，最小二乘网格法可以提供视觉上的平滑性，使填充后的模型更加自然。

其中，di为顶点vi的1 环邻域顶点数。当式（1）成立时，顶点vi则位于其1环邻域的中心处。

由于vi位于三维空间中，该方法可以用矩阵表示，如下所示：

其中，x、y和z为包含n个顶点n×1 维向量，L为n×n的Laplace矩阵，其具体形式为：

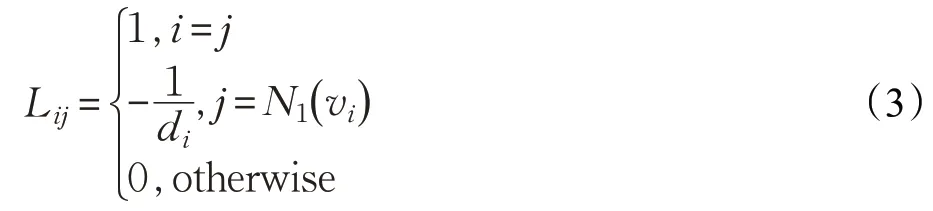
在式（3）中，矩阵L的秩为n-k,n为网格顶点数目，k为网格连通区域的个数。为使方程有解，需加入个控制顶点坐标vs作为方程的边界条件，本文将孔洞区域的边界顶点作为控制顶点，则线性方程的表达形式转换为：

其中，

当矩阵A满秩时，使下式最小化即可求得x：

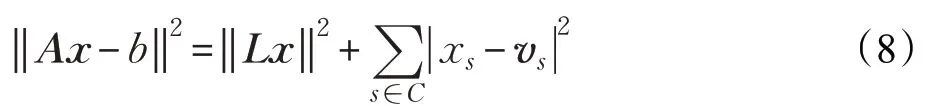
在式（8）中，等式右边第一部分是使得每个顶点位于其1环邻域顶点的中心，第二部分是为了使控制顶点的位置满足要求。

当矩阵A满秩时，该方程的唯一解为ATb，因此，当ATAx=ATb时 ‖Ax-b‖最小，对系数矩阵进行因式分解，可以得到ATA=RTR。其中R为上三角矩阵，则通过求解三角线性方程RTX=ATb和Rx=X即可求得x，同理可求得y和z。

径向基函数（Radial Basis Function，RBF）网络能够解决空间散乱数据点的平滑插值问题，使填充模型更加接近于原始模型。其输入由构成，隐层单元由输入x和已知坐标点坐标计算得到的基函数构成，输出层由一个或多个线性单元组成，表示为多个基函数的线性组合：

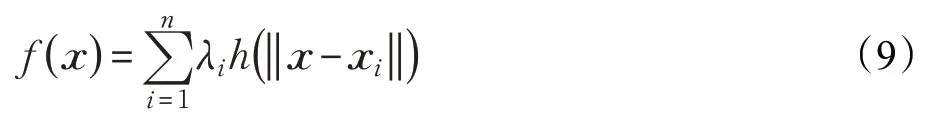
其中，λi表示RBF的组合系数，通过已知的坐标点坐标求得最优解。

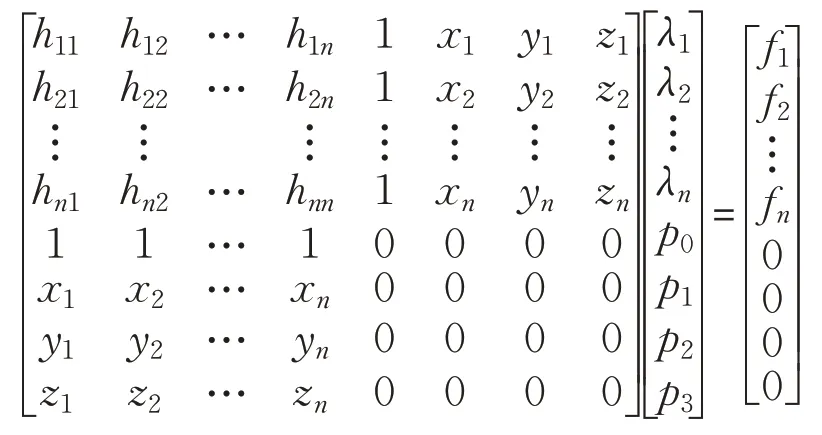
为得到三维网格模型，采用牛顿迭代法将网格顶点映射到隐式曲面上。若取，则式（10）变为：

算法具体过程如下所示。

算法1 高精度的孔洞填充

步骤1 确定孔洞边界，若三维网格模型的边只连接一个三角面片，则该边为孔洞边界边。

步骤2 采用最小角度法填充网格模型。计算边界边长度的平均值ˉ，若具有最小夹角的边界点的两条边界边的距离d ＜2×，则增加一个三角形，反之则增加两个三角形。

步骤3 采用最小二乘网格法优化已生成的顶点位置。

步骤4 采用RBF 网络和牛顿迭代法优化模型，获得填充后的三维网格模型。

2.2 填充三维模型检索

2.2.1 填充三维模型曲率计算

在提取三维点云模型的几何信息时，主要通过直接计算法和最小二乘拟合算法获取点云的局部n次曲面。点云的局部曲面有两种表示方法：一是基于法向距离的局部曲面表示；二是基于欧氏距离的局部曲面表示。基于孔洞填充的残缺三维模型检索方法利用点云模型的坐标信息，采用基于欧氏距离的局部曲面表示法获取点云模型的曲率。曲率是描述三维模型形状的重要属性[14]，准确的坐标信息提高了对模型描述的精确度，进而提高了三维模型检索时的准确率[15]。

2.2.2 填充三维模型聚类

基于孔洞填充的残缺三维模型检索算法将三维模型看作由几个点集组合而成的整体，每个点集内的点都具有较高的相似度，点集间相似度较低。因此，在三维模型检索时，可以采用类间匹配的方法，计算两个三维模型的类间曲率距离，从而使具有最高相似度的两个类相互匹配。对于填充三维模型M1和其他不同的三维模型M2,M1和M2应该具有相同的聚类数目，才能保证M1和M2中的类可以一一匹配。

经典聚类算法中，K-means聚类算法以其简单快速的优势得到广泛应用，但由于K-means聚类算法对初始聚类中心的选择是随机的，当两个聚类中心相聚比较近时，最终的聚类结果可能不太理想。因此，本文使用K-means++聚类算法，在K-means 聚类算法的基础上，首先随机选择一个点作为初始聚类中心；然后计算其他点到该聚类中心的欧氏距离，并计算其他各点适合作为聚类中心的概率，选择具有最大概率的点作为第二个聚类中心；重复此过程，直到选出K个聚类中心为止；最后，以聚类中心对每个数据点的影响为标准对三维模型进行聚类。K-means++聚类算法选取的初始聚类中心进行了优化，使初始聚类中心不是完全随机选取，而是选择距离已有聚类中心较远的点作为下一个聚类中心。该算法的时间复杂度为O( )n，其中n是样本数量，算法执行效率比较高。

具体聚类过程如下：

然后，计算每个点成为下个聚类中心的概率，计算公式如下：

重复这一过程，直到选出K个初始聚类中心为止。

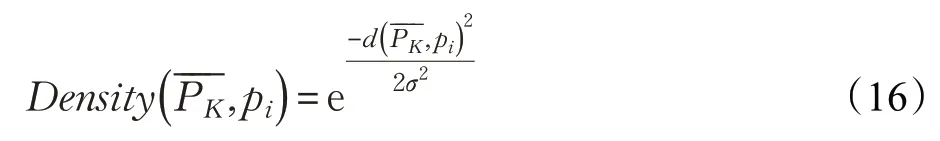
在一次聚类完成后，需要重新计算聚类中心的坐标，计算公式如下：

最后，计算新聚类中心对其他各点的影响值，并重新进行聚类，重复这一过程，直到聚类结果不发生改变为止。聚类过程结束后，最终结果即为具有相同聚类数目的三维模型M1和M2。

2.2.3 填充三维模型匹配

聚类过程结束后，三维模型M1和M2分别由相同聚类数目的类簇组成，类簇内的点具有较高的相似度，类簇间的点具有较低的相似度，因此M1的类簇和M2的类簇也存在相似度高低的问题。由此，计算三维模型M1和M2的相似度可以转化为计算M1的类簇和M2的类簇的相似度，并对M2中的每一类设置标记位，若M2中的某一类k2与M1中的某一类k1相似度最高，则将的标记位设置为1，不再参与M1中其他类的相似度计算，从而提高了计算效率。

在三维点云模型中，类簇即为点的集合，计算类簇之间的相似度，即计算两个点集之间的相似度。计算点集间距离最常用的方法是计算两点集间的Hausdorff距离。假设空间中有两点集，则A和B之间的Hausdorff距离为：

该方法的主要思想是对任意的类k1∈M1，分别计算k1与M2中标记位不为1的类之间的距离，称该距离为类间曲率距离，记为，在M2所有标记位不为1的类中，选择与k1具有最小的类作为k1匹配类，将匹配类的标记位设置为1，在进行M1中其他类匹配时，标记位为1 的类不再参与匹配计算；所有类均匹配完成后，将所有的相加，结果记为C_DIS，C_DIS即为M1与M2的相似度。该方法的具体计算过程如下。

M1中第k1类的类间曲率距离为：

对任意的类k1∈M1，应计算k1与M2中所有标记位不为1的类，从中选择具有最小的类与k1匹配，并将匹配类k2的标记位设置为1。

然后，计算C_DIS。三维模型M1和M2中的类一一对应后，此时每个均为最小值，M1和M2的类间相似度最高，因此将K个相加，M1和M2的相似度也为最高，计算公式如式（14）所示。

3 实验及结论

3.1 实验结果

实验使用 Matlab R2016a、Visual Studio 2017 和OpenGL编程环境实现计算曲率特征、模型分类、模型匹配和显示模型，实验平台为Intel i7-6700 3.40 GHz CPU、8 GB 内存的IBM PC 机。实验使用斯坦福大学三维模型数据库，以填充后的三维模型Bunny为三维检索模型M1,三维检索模型M2为grey rabbit、hare、smile Bunny、cat、bird、bicycle、Armadillo 和 buddha。图1 展示了完整三维网格模型、残缺三维网格模型及填充三维网格模型，图2展示了三维检索模型M2的点云模型。

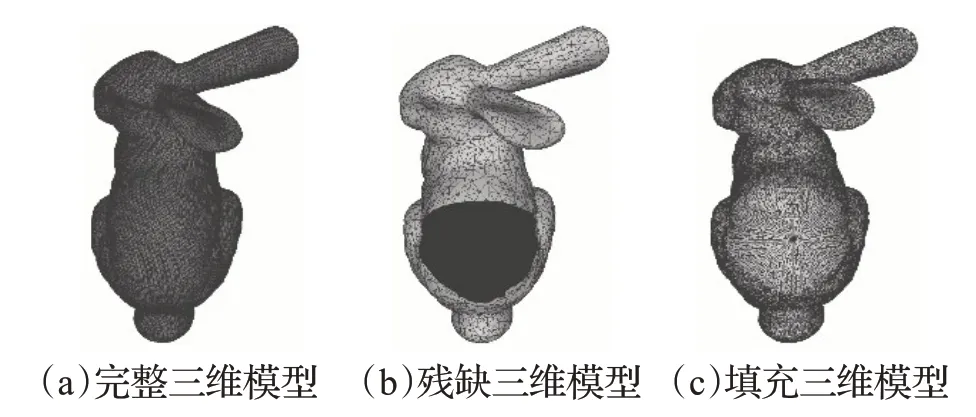
图1 三维模型的网格模型图

图2 三维检索模型M2 的点云模型图

由图1可以看出，填充后的三维模型虽然也是完整三维模型，但是其拓扑结构与完整三维模型相比已经发生改变。因此，填充三维模型有形状关联的作用，可以作为残缺三维模型与其对应的完整三维模型的过渡模型。

为探究拓扑结构的改变是否会对三维模型聚类结果造成影响，将填充三维模型和对应的完整三维模型分别进行聚类，聚类数目K分别取10、9、8、7、6。聚类结果如图3所示。

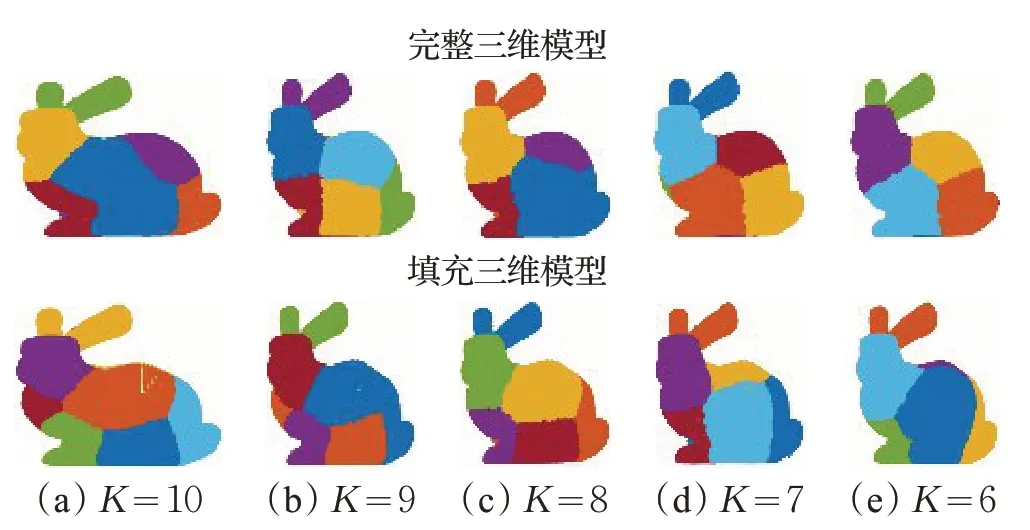
图3 填充三维模型与完整三维模型在不同K 值下的聚类结果

由图3 可以看出，在相同K值下，填充三维模型与其对应的完整三维模型的聚类结果不完全相同，主要的差异体现在孔洞及其周围区域，填充三维模型与其对应的完整三维模型的聚类结果差别最为明显，而远离孔洞区域的部分，如耳朵、脸部等区域，填充三维模型与其对应的完整三维模型的聚类结果差别不大。由此可以看出，拓扑结构的改变会导致聚类结果发生变化。

拓扑结构的改变导致聚类结果发生了改变，是否会进一步对检索结果有较大影响，以及不同的聚类数目K对填充三维模型的检索结果是否也存在影响。为探究以上两个问题，表1和表2分别列出了在取不同的K值时，完整三维模型和填充三维模型进行检索时的C_DIS结果。

表1 完整三维模型的C_DIS结果

表2 填充三维模型的C_DIS结果

由表1 的实验结果可知，当K固定时，在三维检索模型M2中，按照与完整三维模型的相似度由高到低的顺序，依次为hare、grey rabbit、smile Bunny、cat、Armadillo、buddha、bird 和 bicycle。由表 2 的实验结果可知，当K固定时，在三维检索模型M2中，按照与填充三维模型M1的相似度由高到低的顺序，检索结果与完整三维模型的检索结果相同。当K取不同值时，表1和表2的检索结果不变，并按照与M1为同类生物、与M1为不同类生物的顺序排列，在与M1为不同类生物中，又按照生物、非生物的顺序排列。

根据表1 和表2 的实验结果，可以画出以聚类数目K为X轴，以 C_DIS 为Y轴的折线图，如图4所示。

由图4可知，从总体来看，在K取不同值时，无论是填充三维模型还是其对应的完整三维模型，C_DIS 结果基本保持稳定，受K值变化的影响不大。因此，即使在不知道事先应将模型聚为几类的情况下，也能得到较为准确的检索结果。从检索结果来看，虽然不同K值下检索结果稍有差异，但与Bunny属于同类生物的grey rabbit、hare 和 smile Bunny 的相似度要高于与 Bunny 属于不同类生物的三维模型，检索结果基本稳定，准确率比较高。

为了更直观地描述填充三维模型与其对应的完整三维模型检索结果的对比关系，图5绘制了填充三维模型和其对应的完整三维模型与每一个三维检索模型检索时的K-C_DIS折线图。

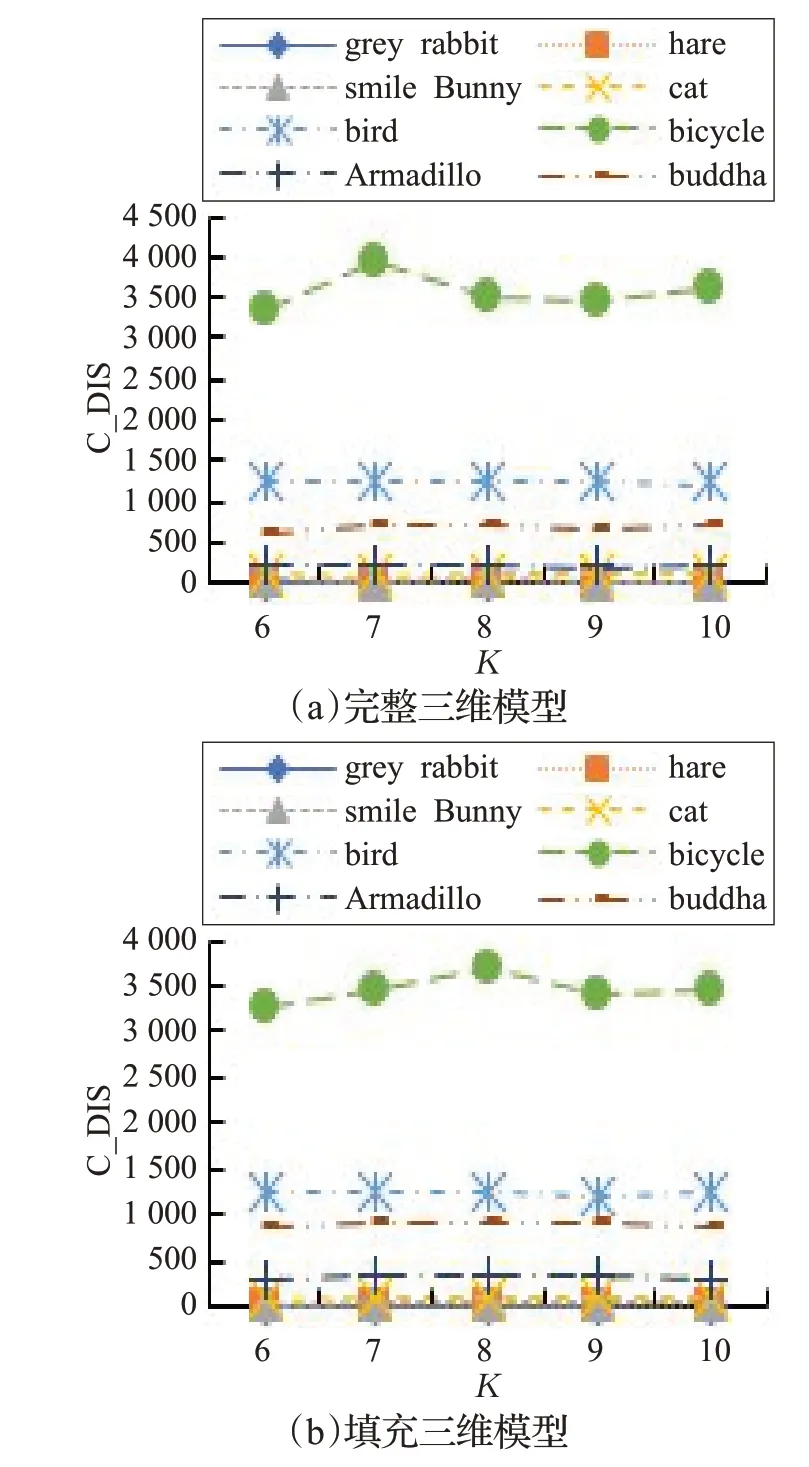
图4 K-C_DIS折线图

由图5可知，三维检索模型与填充三维模型的检索结果与其对应的完整三维模型检索结果的差异均保持在一定范围内，由此可知，在一定误差范围内，残缺三维模型可以通过填充成为完整三维模型进行检索，其检索结果可以作为对应的完整三维模型检索结果使用。

3.2 性能分析

实验过程可以分为孔洞检测、孔洞填充、模型聚类和模型匹配四部分。以残缺三维模型Bunny为例，孔洞检测和孔洞填充所用的时间如表3所示。

表3 孔洞检测和孔洞填充所用时间

在模型聚类阶段，取不同K值时聚类所用时间如表4所示。

表4 取不同K 值时聚类所用时间

在不同K值下，模型匹配所用时间如表5所示。

在完整的三维模型检索过程中，孔洞检测和孔洞填充所需时间占完整实验所需时间的比例如表6所示。

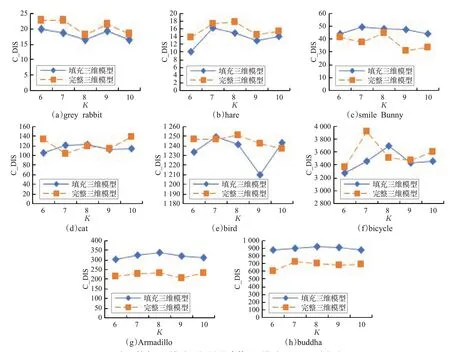
图5 填充三维模型和其对应的完整三维模型K-C_DIS对比图

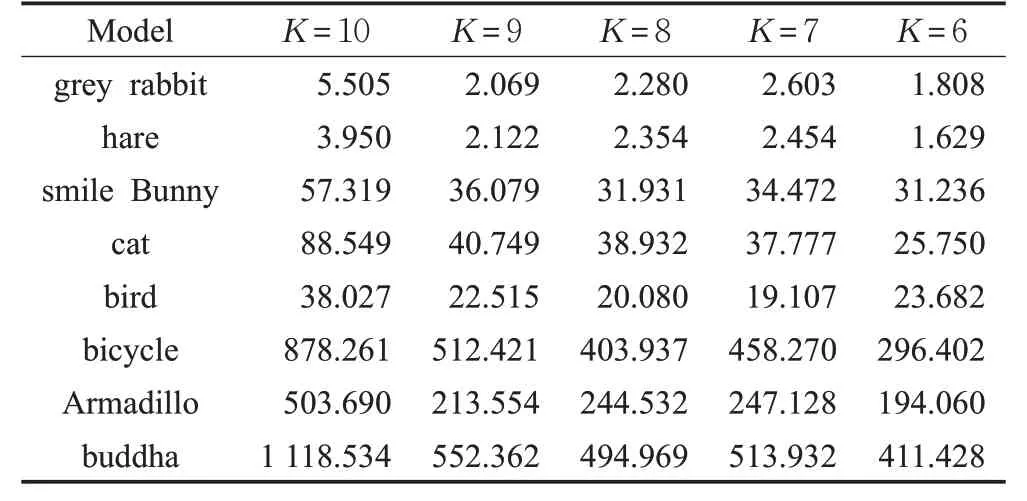
表5 不同K 值下模型匹配所用时间 s

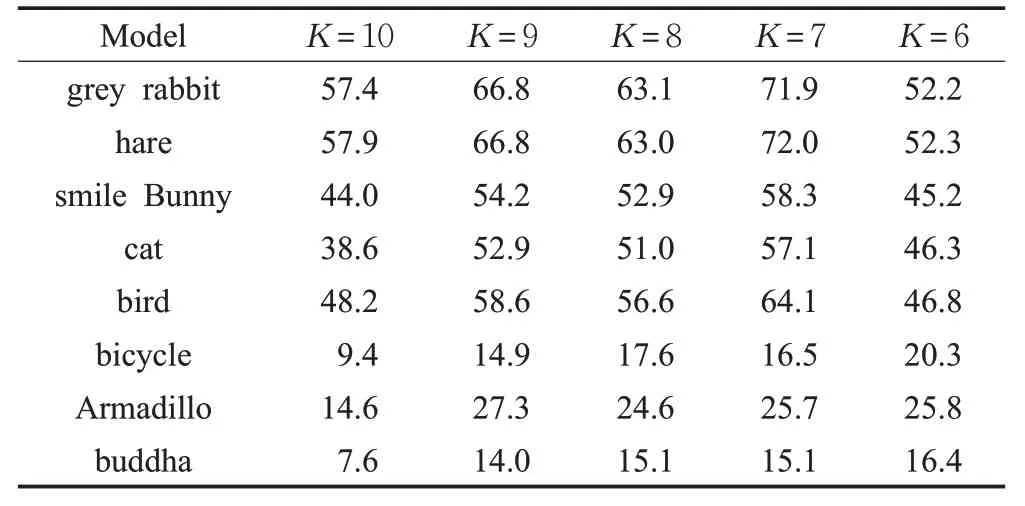
表6 孔洞检测和孔洞填充所需时间占比 %

由表5 和表6 的数据可知，当检索模型的数据集大小与被检索模型的数据集大小相差不大时，孔洞检测和孔洞填充所需时间占完整实验运行时间的比例集中在50%左右，最高可达到70%以上，所占比例较高；当检索模型的数据集大小远大于被检索模型的数据集大小时，孔洞检测和孔洞填充所需时间占完整实验运行时间的比例集中在20%左右。虽然孔洞检测和孔洞填充所用时间占完整实验所用时间的比例大幅下降，但模型匹配过程所用时间却大幅增长，因此，孔洞检测和孔洞填充所占比例相对而言呈现下降趋势。

4 结束语

基于孔洞填充的残缺三维模型检索方法以残缺三维模型为研究对象，通过填充残缺三维模型建立与其对应的完整三维模型的形状关联，从而实现对残缺三维模型的检索。从检索结果来看，填充三维模型检索结果与其对应的完整三维模型检索结果差异较小，在一定误差范围内，填充三维模型的检索结果可以作为与其对应的完整三维模型的检索结果使用。因此，本文算法既适用于残缺三维模型，也适用于完整三维模型，检索方法具有鲁棒性。此外，通过填充，使残缺三维模型在外观上尽可能接近对应的完整三维模型。因此，填充三维模型和对应的完整三维模型曲面弯曲程度基本保持一致，曲率能够较好地描述填充三维模型的特征。最后，根据聚类中心对每个数据点的影响进行聚类，采用类间匹配的方法计算模型相似度，避免了重复计算每个点与其他数据点的距离，提高了计算效率。