基于生成对抗网络的抗泄露加密算法研究
2020-05-20李西明吴嘉润吴少乾郭玉彬
李西明,吴嘉润,吴少乾,郭玉彬,马 莎
华南农业大学 数学与信息学院,广州 510642
1 引言
抗泄漏密码学是伴随着侧信道攻击技术而产生的,其主要关注的是如何设计可以抵抗各种侧信道攻击的安全密码方案,用于消除秘密信息泄露对方案安全性的影响。2004年Micali和Reyzin提出的唯计算泄露模型[1]对抗泄漏密码学研究具有开创性的意义。而Akavia 等人在文献[2]中提出的弱密钥泄露模型降低了构造安全的抗弱密钥泄露攻击的密码方案的难度。Naor和Segev在文献[3]中提出在弱密钥泄漏模型中选择明文安全的公钥加密方案,使得抗泄漏密码学可以扩展到更多的应用场景。近年来,国内相关研究者也集中研究了密钥连续泄漏情况下密码系统的安全问题[4-6]。
生成对抗网络(Generative Adversarial Networks,GANs)由一个生成模型和一个判别模型组成,其核心思想是让生成模型和判别模型对抗学习,两者进行博弈,使得两者在互相对抗过程中不断强化,最后得到能够生成以假乱真数据的生成模型。自Goodfellow等人[7]提出后,GANs 已被广泛应用并取得了很好的成绩,其中应用效果最好的是在计算机视觉领域,包括图像生成及分割[8]、图像风格迁移[9]等。另外,在信息检索[10]、文本生成[11]等领域中也取得了令人瞩目的成果。
2016 年 Google Brain 团队 Abadi 等人利用生成对抗网络进行了安全通信方面的研究[12]。该加密通信模型由两个互相通信的神经网络Alice 与Bob,以及一个窃听者神经网络Eve 组成。当Alice 与Bob 进行加密通信时,尽量限制Eve从窃听Alice和Bob之间的通信中获得信息。在训练过程中,Alice 与Bob 在保证明文加密解密准确无误的情况下尽力提高加密解密复杂度,而Eve则尽量使自己的解密结果与明文相近,提高解密的准确性。通过对抗训练,可得到一个能够保证正常通信并抵抗窃听的加密通信模型。
本文研究使用生成对抗网络来解决密钥部分泄漏情况下安全加密通信问题。首先提出了基于生成对抗网络的抗泄漏密码学的基本架构,然后使用文献[12]的Alice、Bob 和 Eve 在 16 位密钥对称加密方案下,泄露1比特密钥时,模型基本可以实现安全的加密通信。进而对通信双方及敌手的神经网络模型进行增加全连接层、修改激活函数以及数据批规格化等方面的改进,改进后的神经网络模型通过对抗训练可实现8 比特及以下密钥信息泄漏的安全保密通信。
2 GANs加密通信
Abadi等人在文献[12]中把对称加密系统通信双方Alice与Bob以及敌方Eve均设计为神经网络模型,并通过GANs 实现了在敌手监听情况下的加密安全通信。其工作始于经典的密码学场景,如图1所示[12]。Alice与Bob 进行加密通信。Alice 利用密钥K(Key)对明文P(PlainText)加密生成密文C(Ciphertext)。Bob 与 Eve均能够完整获取密文C。Bob通过密钥K对密文C进行解密,解密后获得消息PBob。Eve在没有密钥情况下对密文C解密,得到消息PEve。Alice 与Bob 组成的加密通信模型与Eve 的敌手模型在对抗训练过程中不断优化,最终使消息PBob与明文P完全相等,而PEve与P的差异尽量大。
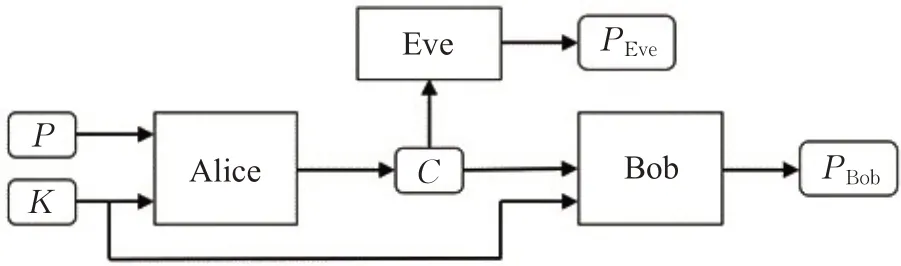
图1 安全加密通信中的Alice、Bob和Eve
图2 给出Abadi 等人实验中使用的神经网络模型,其中Alice和Bob模型相同,Eve的神经网络模型增加了一层全连接层用以模拟生成密钥的过程。Alice输入为P和K,加密输出为C。Bob 输入为C和K,解密输出为PBob。Eve 作为敌手对信息进行窃听,输入为C,解密输出为PEve。Alice与Bob通过训练共同提升加密解密能力,保证解密结果PBob=P,敌手Eve 通过训练提高解密能力,其目标是PEve=P,而实际训练中降低PEve的损失率,使得PEve尽量接近P。通信方与敌手的对抗表现为在训练过程中互相反馈,Eve的训练结果用于下一轮Alice 和Bob 的加密解密训练,Alice 和Bob的训练结果用于Eve的下一轮解密训练,从而提高加密通信方案的安全性。
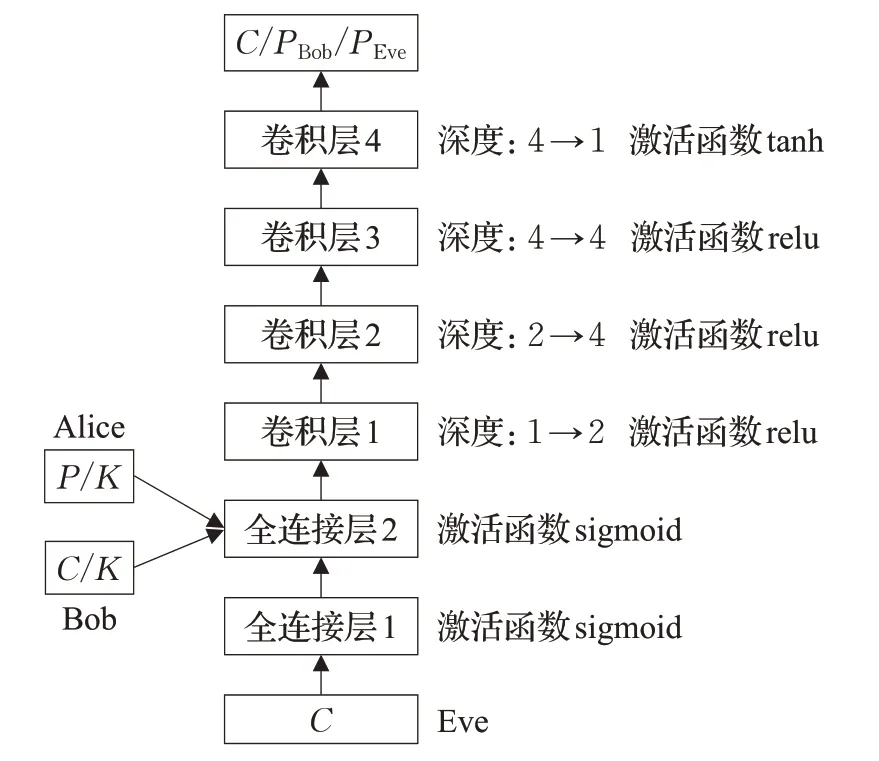
图2 Alice、Bob和Eve的神经网络结构
其实验在16 位明文(每比特取值为1 或-1)、16 位密钥对称加密条件下进行,通过对抗训练,通信双方可正常通信,即保证PBob=P,而Eve 解密结果保持与明文的差异在7~8比特之间,即解密结果与随机生成的结果相似,未获取更多有用信息。
为计算Alice 与Bob、Eve 解密结果与明文的差距,同时给出明文与解密明文之间的距离。设N为明文P和解密明文P0的长度,则P与P0之间的距离定义为:


因为Bob与Alice需要抵抗Eve的破解,所以损失需要涉及到Eve的损失LEve。通信方信息损失记作LBob,其计算公式定义为式(3)。
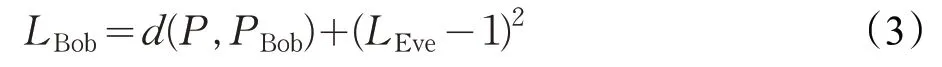
3 GANs抗泄露加密通信
为描述方便,本文首先给出基于生成对抗网络的抗泄露加密通信系统结构,如图3 所示。图3 中,Alice 与Bob是通信方,Alice利用密钥K对信息P进行加密,生成密文C。Bob 接受密文C,利用密钥K进行解密得到明文PBob(在此不考虑使用的是对称加密还是非对称加密方案,因为无论何种加密方案,加密和解密密钥都是已知的)。Eve 是敌手,他通过监听或获取密文C与部分泄露的密钥LK,利用C和LK解密得到明文PEve。Alice、Bob和Eve是具有相同计算能力的神经网络,因为通信方Alice、Bob具有完整密钥,无疑通过神经网络训练,可实现正常通信。Eve窃取密文C和部分密钥LK,通过训练可获取尽量多的信息。抗泄漏加密通信的目标是通过神经网络设计和对抗训练实现Alice、Bob 双方正常通信,而Eve 无法得到比随机猜想更好的解密结果。极端情况下,即使Eve拿到16比特密钥中的15比特,依然无法解密得到明文P,而Alice和Bob依旧保持正常通信。
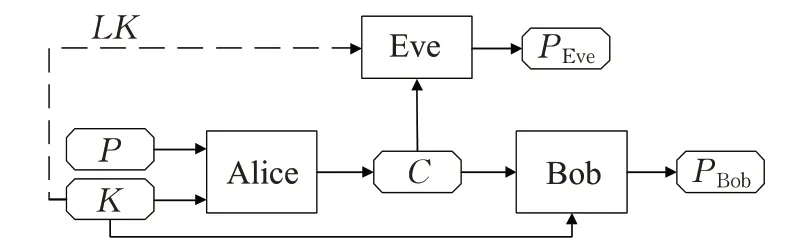
图3 抗泄露加密通信场景
本文首先使用Abadi 等人给出的Alice 与Bob 的神经网络模型,如图2所示。图2中Eve模型的全连接层1是用来推测密钥的,但在本文抗泄露加密通信中它已获取了一个泄漏i比特的密钥,同时假设ABC三方具有相同的计算能力,因此设定Eve 与Alice、Bob 的神经网络模型相同,并为其增加一个新的输入,即泄露i比特的密钥LK。三方神经网络模型与输入输出见图4。

图4 Alice、Bob和Eve初步的抗泄漏加密通信模型
本文在密钥泄露1 比特、2 比特的情况下对通信双方和敌手进行对抗训练。实验中Alice、Bob和Eve均采用AdamOptimizer 优化器进行模型优化。对抗训练按轮进行。模型的学习速率均设为0.000 8。Alice的输入端由明文P和密钥K组成,Bob 的输入端由密文C和密钥K组成,Eve的输入端由密文C与部分密钥LK组成。其中P、K、LK和C均用长度为N的数组表示,检测时N取16。P和K中每一位随机取值为-1 或1。随机选取密钥K中的n位,生成部分泄漏密钥LK,n代表密钥相同的位数,剩余位由随机数生成。如下为模型的伪代码。
Alice网络搭建:
(1)明文与密钥K横向拼接作为Alice 的输入(设明文与密钥长度均为N);
(2)Alice 输入传入2N×2N的全连接神经网络,输出经过激活函数sigmoid;
(3)卷积层1过滤器大小为4×1,扫描后输出的网络深度为2,步长为1,激活函数为relu函数;
(4)卷积层2过滤器大小为2×2,扫描后输出的网络深度为4,步长为2,激活函数为relu函数;
(5)卷积层3过滤器大小为1×4,扫描后输出的网络深度为4,步长为1,激活函数为relu函数;
(6)卷积层4过滤器大小为1×4,扫描后输出的网络深度为1,步长为1,激活函数为tanh函数;
(7)输出的结果为密文C。
Bob网络搭建:
(1)密文C与密钥K拼接作为Bob输入(设密文与密钥长度均为N);
(2)Bob 输入传入 2N×2N的全连接神经网络,输出经过激活函数sigmoid;
(3)采用与Alice完全相同的卷积网络结构。
Eve网络搭建:
(1)把密钥K中的随机x位数赋值到泄漏的密钥K′中作为泄漏的信息,其他数用随机数生成,得到泄漏的密钥K′;
(2)密文C与泄漏的密钥K′拼接作为Eve的输入;
(3)Eve输入传入2N×2N的全连接神经网络,输出经过激活函数sigmoid;
(4)采用与Alice完全相同的卷积网络结构。
首先对Alice和Bob 进行加密解密训练,训练2 000次,稳定后利用其训练结果对Eve 进行解密训练,同样训练2 000次可达到稳定。下一轮利用Eve的解密结果对Alice 和Bob 进行加密解密训练,再利用其训练结果对Eve进行解密训练。此训练共进行10轮,训练结果如图5所示。
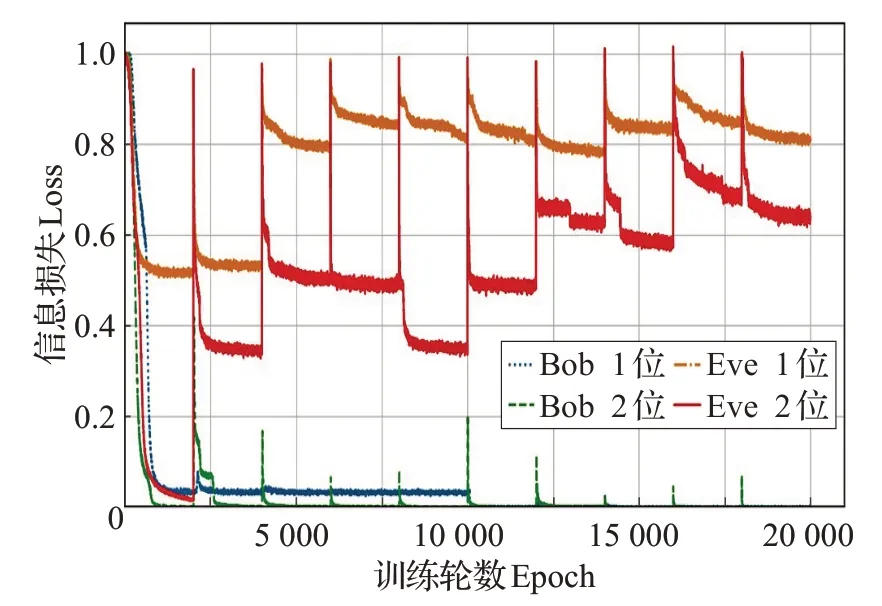
图5 模型的抗泄露训练结果
图5 中,在泄漏1 比特密钥时Alice 和Bob 在训练5轮以后可达到稳定,信息损失率接近0,而Eve 经过10轮训练其损失率仍保持在0.80~0.85之间,接近最好值1。依据式(2),此时Eve 解密正确的比特数约占明文长度的40%~50%,接近随机猜想的正确位数。此情况与原加密通信方案没有密钥泄露的情况相比,Eve获得了稍多一点的信息,但远无法达到完全解密的程度。泄漏2比特密钥时,Alice和Bob在训练2轮以后可达到稳定,比泄露1 比特密钥训练速度快。Eve 经过10 轮训练后可达到稳定,但其信息损失稳定在0.6~0.7 之间,即Eve解密正确的比特数约占30%~35%,由于明文取值仅有1和-1,此情况等价于解密正确位数占的比例65%~70%,此时泄漏信息略多,不再是一个可接受的抗泄露加密通信方案。
4 增强的抗泄露加密模型
抗泄露加密通信的关键在于部分密钥泄漏,既要保证通信双方Alice和Bob的正常通信,又要保证在Eve得到部分密钥情况下无法正确解密。由上文实验可知,Abadi等人给出的神经网络模型在泄露1比特密钥情况下勉强可用,但泄露2比特及以上时,无法使用,因此无法直接用来解决抗泄露加密通信问题。本文从改进激活函数、增强神经网络功能以及批规格化三方面对此模型进行改进,并通过实验来验证抗泄露加密模型。
4.1 改进激活函数
分析实验过程,在泄漏密钥位数增加时,图4中Eve神经网络模型的损失下降显著,说明Eve越来越容易破解密文了。模型中使用relu 激活函数容易导致神经元死亡现象,通过对模型中死亡神经元个数统计得出,Alice与Bob 死亡神经元比例约为34%,Eve 的死亡神经元比例为50%。死亡神经元出现原因在Xu 等人的文献[13]中已指出。
以下给出修改激活函数的具体原因。图6为relu与leaky relu 的函数图像,由图可知,relu 函数在输入为负数时输出的结果恒为0,因此relu 函数在负半轴的导数也恒为0。由于神经网络的权值更新是通过反向传播实现的,而反向传播即通过计算损失E对权值w的偏导数来更新权值,当神经元的输出为负数时,relu 的导数必然是0,因此权值w将不会进行更新。正因如此,使用多层relu 神经网络(若都使用relu 作激活函数)的时候,容易出现大面积的神经元死亡,即大部分的神经元不再更新权值,代表神经网络的学习进程停滞。本文提出使用leaky relu 函数,因为此函数在负半轴的导数不恒为0,有效地保证当输入落在负半轴时损失E对权值w的偏导数不恒为0,权值依然能够进行更新,避免由于神经元死亡而导致的学习进程停滞的问题。故将模型中所有卷积神经网络的relu 激活函数修改为leaky relu函数,其余部分结构不变。
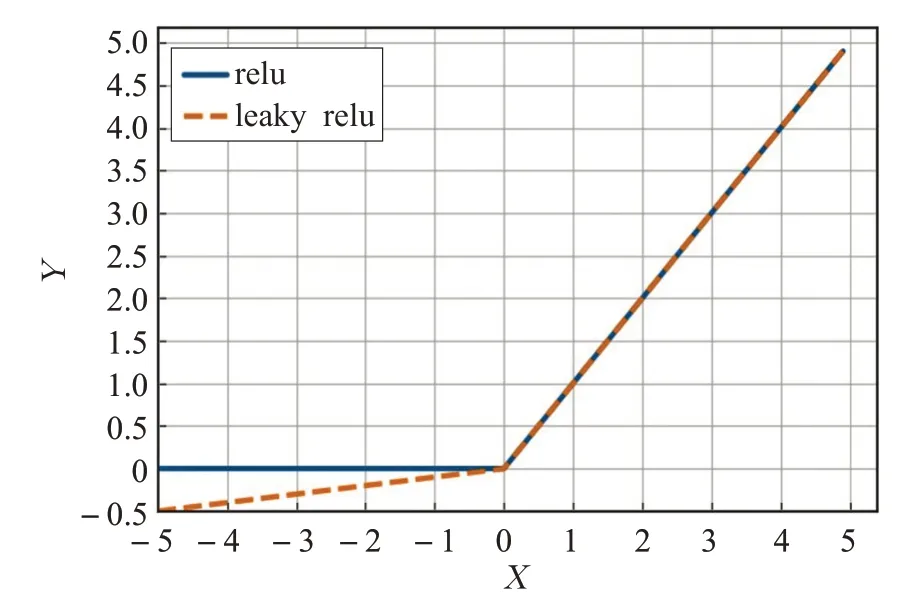
图6 relu与leaky relu激活函数
图7 给出修改激活函数后,1~5 比特密钥泄露情况下的训练结果。为描述方便,图7 横坐标改为轮数,每轮训练中首先对Alice 和Bob 的加密解密进行训练,再利用训练结果对Eve 进行训练。每轮训练对Alice 和Bob、Eve 各训练2 000 次。实验过程中发现对3 个网络的训练都可以2 000次以内达到稳定状态。从图7中可以看出,修改激活函数之后模型的能力得到提升,且没有出现Bob无法解析密文的情况。Eve在1、2比特密钥泄露情况下训练较为平稳,均可达到接近0.9 的信息损失。当Eve 已知位数达到3 和4 后信息损失出现波动,无法进入平滑优化。据统计,死亡神经元的比例下降了约1%。同时因为修改激活函数后减少了死亡神经元的出现,所以模型的训练时间也有所增加,增长比例约为5.7%。
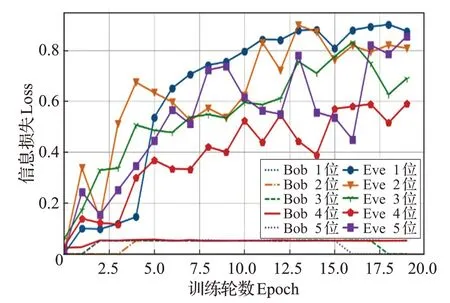
图7 测试1~5比特密钥泄露的运行结果
4.2 增强模型的复杂性
通过上一节的操作,把安全通信的密钥泄漏提高到了2 比特,密钥泄漏比特数进一步提高后,就无法进行安全通信了,也就是说,Bob和Eve都不能正确解密Alice发送的密文。这说明,接收网络和敌手网络被加密的信息迷惑,网络解密能力达到了极限。如果增强Bob 和Eve的网络模型,其解密能力就能提高,但是由于Eve只有部分密钥,其解密能力的提升程度应该低于Bob。为验证这一想法,通过增加全连接层的方法来同步增加Bob与Eve的解密能力,保证Bob与Eve的解密能力一致。
模型修改:对Bob 和Eve 的神经网络模型在图4 基础上增加全连接层2,激活函数取tanh函数,他们的输入输出保持不变。Alice 神经网络和输入输出都保持不变。同时按4.1节对3个神经网络的卷积层1~3,将激活函数修改为leaky relu函数。
以下给出使用tanh 的具体原因。图8 为sigmoid 与tanh 函数的导函数图像,由图可知sigmoid 导函数的值域在[0,0.25],而 tanh 导函数的值域在[0,1]。因为 sigmoid 的导数最大为0.25,所以在更新权值、计算偏导数的过程中必然也乘了一个小于等于0.25 的值。因此这样计算出来的偏导数会偏小。随着sigmoid 层数的增加,会有更多的数相乘,这种现象会越来越严重,最终导致权值的更新过小,即反向传播的信息量被大量减少,近似于没有任何更新,从而出现死亡神经元,学习进度停滞。本文使用的tanh 的导数比sigmoid 的导数大,因此相比sigmoid,权值更新的值并不会被压缩得太小,神经网络层数增加时,对更新的数值影响也不会太大。因此tanh能够有效地减缓死亡神经元的现象,从而避免神经网络学习进程停滞的问题[13-14]。因此,此处取全连接层2的激活函数为tanh函数,不取sigmoid函数。

图8 sigmoid与tanh的导函数
对1~5比特密钥泄露情况,本文对Alice、Bob和Eve进行训练,训练结果如图9所示。由图9可知,整体上增加全连接层后模型稳定性增强。同时,Bob的解密能力明显增强,经1~3 轮训练后可达到稳定,且其信息损失均接近0。Eve 在1~3 比特密钥泄露情况下训练较为平稳,均可达到0.8 左右的信息损失。但是在4~5 比特密钥泄露情况下Eve信息损失波动在0.4~0.7之间,平均在0.6附近,无法进一步提升。
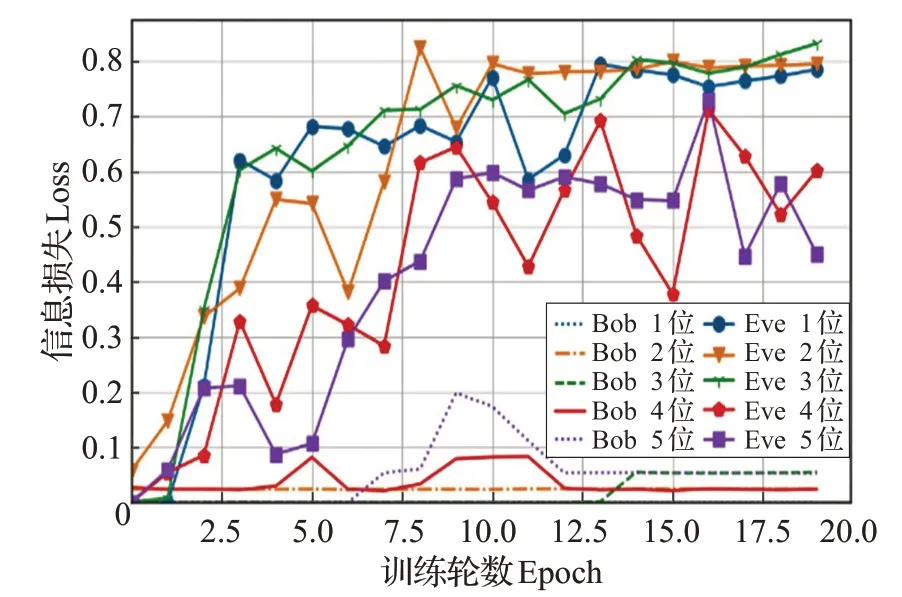
图9 测试1~5比特密钥泄露的运行结果
4.3 数据规格化处理
进一步分析4.2 节的实验结果,模型在增加全连接层后稳定性得到了提升,但很可能陷入局部最优位置。因此考虑对全连接层加入规格化处理来减少数据差异性因素对模型优化的影响,提升神经网络寻找最优解的能力。
数据规格化(Scaling)又称数据尺度归一化[15],就是将数据的取值范围映射到一个特定范围之内,以消除数值型属性因大小范围不一而影响基于距离的分类方法结果的公正性。本文对Bob、Eve 模型的输入数据采用取零均值规格化方法进行处理,取均值为0,方差为1。修改后Alice、Bob和Eve模型见图10。
增加数据规格化处理后,对密钥泄漏1~9比特的情况进行模型训练,结果见图11。由图11 可知,Bob 与Eve 在增加数据规格化后整体解密能力都有较大提高。数据规格化起到进一步增加模型稳定性,同时避免陷入局部最优的作用。Bob的解密能力经过1~3轮训练后可达到稳定,信息损失接近0。Eve在密钥泄漏1~7比特情况下收敛都很快,在训练9 轮后可达到稳定状态,且信息损失可达到0.8左右。密钥泄漏达到8比特时收敛变慢,但信息损失仍可达到0.8 附近。但当密钥泄漏达到9 比特时收敛较慢,经19 轮训练后才基本达到稳定,而信息损失在0.6 附近。可见,图10 给出的模型对1~8比特密钥泄漏,在多轮训练可得到安全的抗泄漏加密通信模型。继续增加密钥泄漏位数情况下,无法得到安全的抗泄漏加密通信模型。
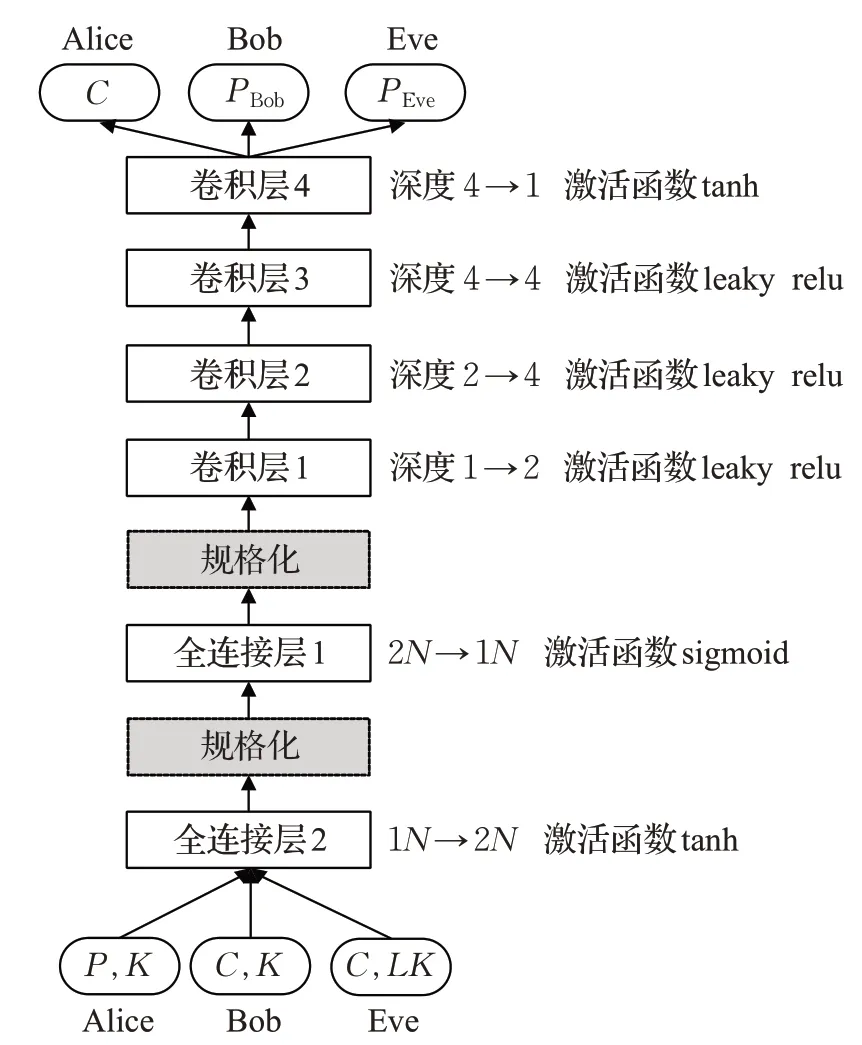
图10 抗泄漏加密通信模型
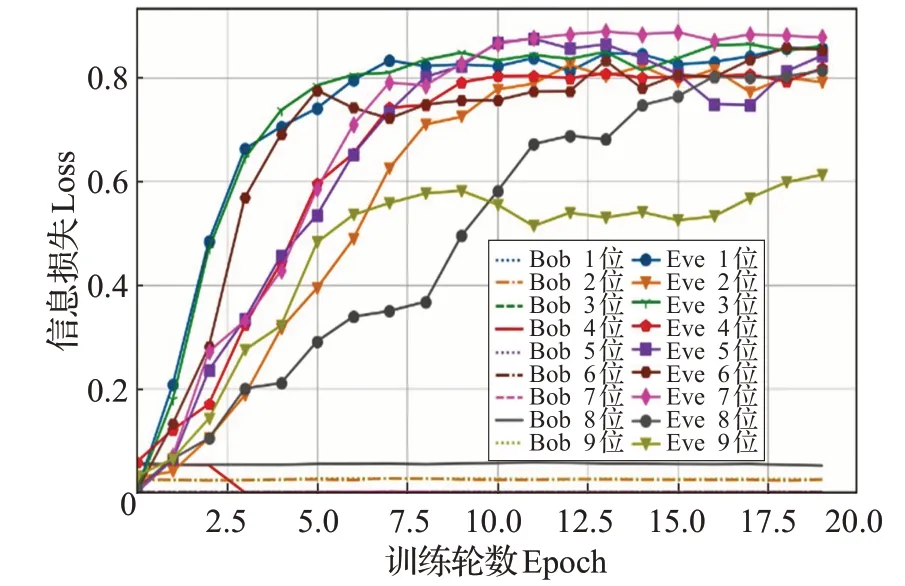
图11 测试1~9比特密钥泄露的运行结果
5 结束语
本文利用神经网络、生成对抗网络解决抗泄露加密通信问题,给出基于生成对抗网络的抗泄露加密通信方案。从Abadi等人的安全加密通信模型出发,通过一系列实验改进,在16位密钥对称加密通信环境中,密钥泄露达到8位时仍可保证安全的抗泄露加密通信模型。
本文为抗泄露加密通信提供了一种全新的解决思路,并通过实验证明了思路的可行性。但本文对神经网络的改进目前仅从提高神经网络复杂性、激活函数和数据规格化方面开展,所使用的方法主要是提高模型整体解密能力和稳定性。
对抗泄漏加密通信问题,还可从更加精巧、更具有针对性的神经网络结构,更强的加解密能力,增加神经网络模型的存储能力等方面入手。期望通过实验实现仅剩余1 比特密钥未泄漏的极端情况下仍能保证安全通信的终极目标。
