优化极限学习机及其在脑卒中TCD数据分类应用

耿银凤，张雪英，李凤莲，胡风云，贾文辉，王 超

1.太原理工大学 信息与计算机学院，太原 030024

2.山西省人民医院 神经内科，太原 030012

1 引言

脑卒中是现代社会中的一种高发性脑血管病，严重危害人类健康和影响人们生产生活，其中缺血性卒中占脑卒中总数的半数以上[1]。因此，在发病早期或者潜伏期，能准确预测缺血性脑卒中疾病发病状况，从而采取适当的措施进行积极的干预治疗显得极为重要。

颅内动脉狭窄已被医学研究证明是缺血性脑卒中的重要诱因之一[2]，经颅多普勒（Transcranial Doppler，TCD）作为一种无创伤的颅内动脉狭窄的筛查检测工具，因其操作方便、价格低廉的特点，在临床上广泛应用于脑卒中疾病的诊断[3-4]。脑卒中的诊断实际上可看作是一个分类问题，随着人工智能技术的发展，许多研究人员希望通过人工智能技术辅助医生进行诊断，避免医生因经验不足产生的错误，提高诊断效率。目前用于TCD 数据分类研究的方法主要有支持向量机（Support Vector Machine，SVM）[5]和人工神经网络（Artificial Neural Network，ANN）[6-8]等。SVM 虽然具有较强的非线性拟合能力，但其分类性能易受输入参数影响[9]；ANN 一般采用梯度下降法（如反向传播算法）对大量样本进行训练，不断迭代调整网络的权值，因而具有很强的学习能力，但其存在收敛速度慢，容易陷入局部极值，对网络初始权值依赖度高等缺点。针对现有TCD分类诊断模型存在的训练速度慢、准确率低等缺点，本文选择极限学习机（Extreme Learning Machine，ELM）作为TCD 数据分类模型，这有利于提高模型训练速度，并增强模型的泛化能力[10]。

ELM 学习算法自产生以来得到了飞快的发展，针对不同的应用场景，分别衍生出了核极限学习机（Extreme Learning Machine with Kernel，KELM）、在线序贯极限学习机及加权极限学习机（Weighted Extreme Learning Machine，W-ELM）[11]等相关算法，并广泛应用于人脸识别[12]、交通信号灯检测[13]、电力负荷预测[14]、遥感影像分类[15]等领域。随着ELM的发展，研究人员逐渐意识到，由于隐含层的输入权值和阈值等参数在ELM学习过程中是随机选择产生的，可能存在部分参数为0 的情况，导致部分隐含层神经元失效。与传统的ANN 算法相比，ELM往往需要更多的隐含层神经元数目，使得网络的复杂度增加；并且ELM 的分类性能易受随机产生的隐含层参数影响。为克服这些缺点，通过应用群智能算法对ELM的隐含层参数进行优化，可以提升泛化性能，提高分类精度，降低网络复杂度[16]。作为一种群智能算法，蝙蝠算法（Bat Algorithm，BA）具有寻优速度快、全局寻优能力强的优点，可避免陷入局部最优。为此，本文提出了一种BA优化ELM的缺血性脑卒中TCD数据分类诊断模型BA-ELM，该模型可以对脑卒中病人的TCD数据进行快速的分类，并达到较高的分类预测精度。

2 ELM基本原理

ELM 是由Huang 提出的一种单隐层前馈神经网络（Single Hidden Layer Feedforward Neural Network，SLFN）训练算法。SLFN作为一种常见的ANN，其用于连接输入层和输出层的隐含层只有一层。与传统ANN不同的是，ELM 的隐含层输入权值和阈值是随机产生而不是通过迭代生成的，并且不需人为设置初始权值和初始阈值等参数，因而大大提高了网络的训练速度，同时克服了ANN易出现的过拟合问题。图1为ELM的网络结构图。

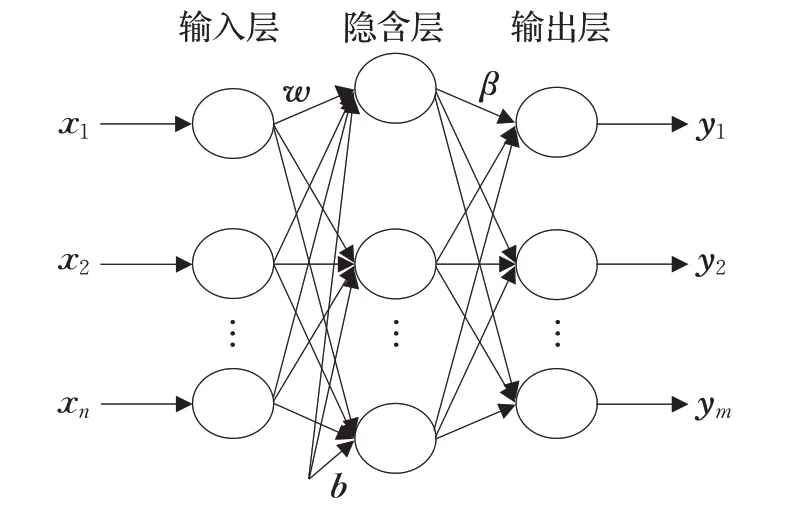
图1 ELM网络结构

对于N个训练样本(xi,ti),xi=[xi1,xi2,…,xin]∈Rn为输入样本，ti=[ti1,ti2,…,tim]T∈Rm表示样本标签，即网络的期望输出。输入层神经元数目为n，隐含层神经元数目为L，输出层神经元数目为m，SLFN 的输入输出关系为：

式中，wi=[wi1,wi2,…,win]T是输入层和第i个隐含层神经元之间连接权值，即隐含层输入权值，bi是第i个隐含层神经元的阈值，βi=[βi1,βi2,…,βim]T是第i个隐含层神经元和输出层之间的连接权值，即输出权值，yj=[yj1,yj2,…,yjm] 表示网络的实际输出，g(·) 是隐含层神经元的激励函数，一般可以从“Sigmoid”“RBF”“Hardlim”等函数中选择。训练ELM 使得样本实际输出零误差逼近期望输出，即：

也就是说，存在βi、wi和bi使得

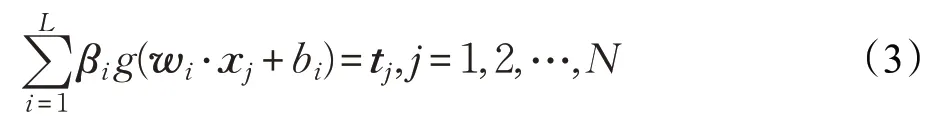
上式进一步写成矩阵形式：

其中，H、β和T分别为：

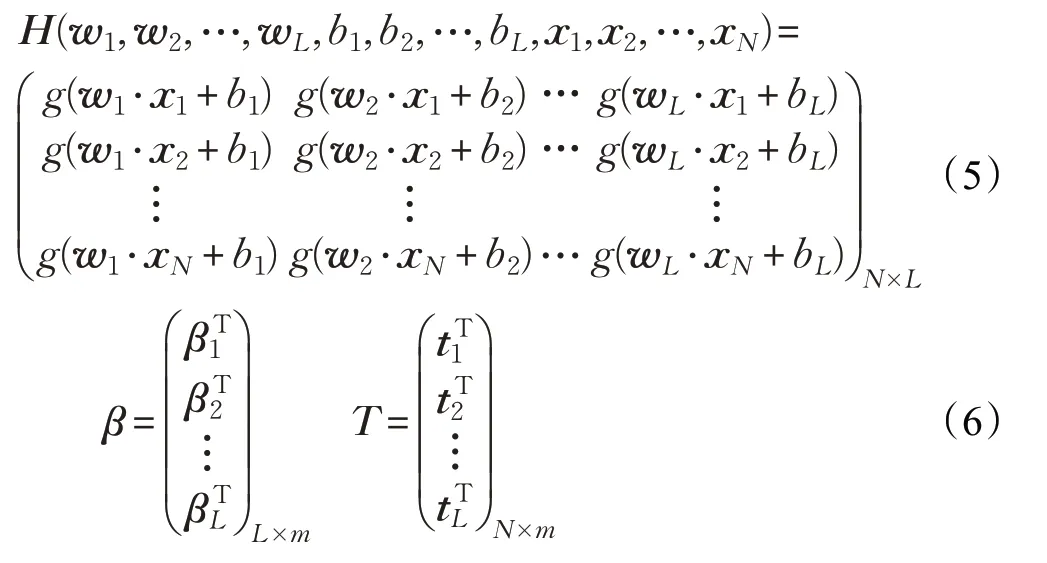
式（4）和（5）中的H是隐含层输出矩阵，Hij表示对应于输入xi的第j个隐含层神经元的输出。由于wi和bi都是随机产生而不是通过训练产生的，其值一经产生隐含层输出矩阵H的各元素值都为确定值，即H为一个确定的矩阵，又因为T是已知值，需要训练的参数只有隐含层输出权值β。极限学习机的学习过程就是根据线性系统Hβ=T求解β的最小范数最小二乘解：

3 BA算法

BA算法是一种群智能算法，2010年由Yang Xinshe受启发于蝙蝠觅食过程中的回声定位而提出[17]。与其他群智能算法相比，BA算法具有寻优速度快、全局搜索能力强等显著优点。该算法的基本原理为：将数目为n的蝙蝠种群映射到D维搜索空间中，n个蝙蝠个体所处的位置即为所求优化问题的n个可行解，将种群中蝙蝠个体搜寻食物时位置更新的过程类比为参数优化过程。该算法的目标是寻找出迭代后种群中最优的蝙蝠个体位置，也即n个可行解中的最优解。

虚拟蝙蝠个体的位置、速度和脉冲频率分别按式（8）～（10）进行更新：

在算法的局部搜索阶段，先产生一个随机数，若该随机数大于脉冲发射速率，则蝙蝠种群按式（11）所示规则在当前全局最优解附近随机扰动产生局部最优解：

式中，ε为[-1,1]间的随机数，At表示n个蝙蝠个体的平均响度。

蝙蝠在飞行过程中会根据与食物距离的远近来调整其脉冲响度和脉冲发射速率，具体表现为：在刚开始觅食时脉冲发射速率较小且脉冲响度大，随着搜寻过程的进行，与食物的距离越来越近，蝙蝠不断降低脉冲响度并增大其脉冲发射速率。脉冲响度和脉冲发射速率的更新规则分别为式（12）和（13）：

其中，α、γ均为常量且满足 0＜α ＜1，γ ＞0 。

4 基于BA优化ELM的TCD数据分类模型

本文给出的BA-ELM 算法基本机理主要是采用蝙蝠算法优化ELM 算法的隐含层输入权值和隐含层阈值，其基本思想为：将ELM的隐含层输入权值和阈值映射为蝙蝠优化算法中各个蝙蝠个体D维空间中的位置矩阵，并设计出BA-ELM网络模型的适应度函数。BAELM 网络模型的最优化问题可以转化为：求解适应度函数值全局最小时所对应的蝙蝠个体，该蝙蝠个体位置即为全局最优解，根据蝙蝠个体位置与ELM 的隐含层输入权值和隐含层阈值的映射关系，即可得到最优的ELM 隐含层参数，按式（4）和（7）很容易求出ELM 的隐含层输出矩阵和输出权值矩阵，从而得到最优的ELM网络模型。基于该算法建立的TCD数据分类模型原理框图如图2所示。

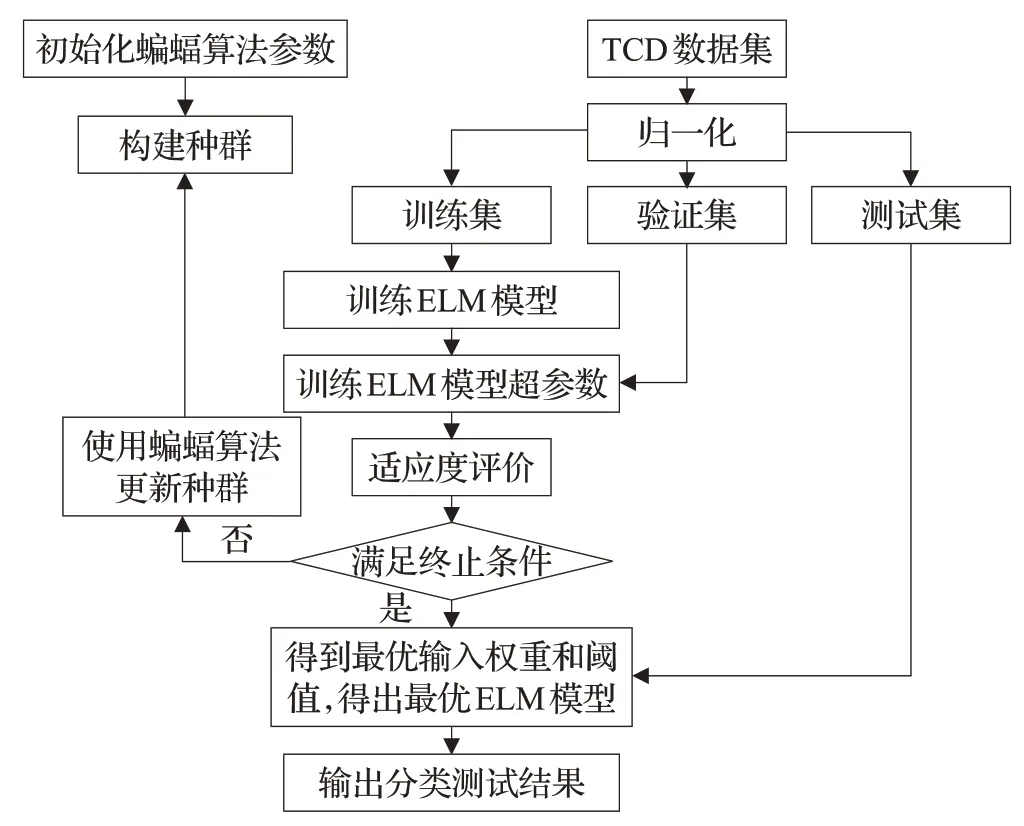
图2 基于BA-ELM的TCD数据分类模型

蝙蝠算法优化ELM的算法流程如下：

训练阶段

输入：具有N个实例的训练集ti∈Rm，xi为具有n维特征的输入样本，ti为第i个实例的类别标签；具有N′ 个实例的验证集。

（1）产生一个蝙蝠个体数为n的初始种群，初始化其脉冲响度Ai，脉冲发射速率ri，并设置最大迭代次数iter_max，搜索脉冲频率范围[fmin,fmax]，响度衰减系数α，脉冲发射速率的增强因子γ等参数（α、γ均为常量且 0＜α ＜1,γ ＞0）。

（2）随机初始化D维空间中蝙蝠种群的位置、速度、频率等参数，其参数产生的随机性正好对应ELM参数中隐含层输入权值和阈值矩阵元素产生的随机性。采用合适的映射方法将ELM的隐含层输入权值矩阵和隐含层阈值矩阵映射成蝙蝠种群的位置矩阵。用训练集来训练得到ELM 的隐含层输入权值、隐含层阈值和输出权值等网络模型参数，利用构建的ELM 网络模型对验证集数据进行分类，以验证集的误分率为适应度函数，找到适应度函数值最小的蝙蝠个体，其位置为当前全局最优。

（3）根据式（8）～（10）所示的更新规则对种群每个蝙蝠个体的位置、速度和脉冲频率进行迭代更新。

（4）产生一个随机数，当该随机数大于ri，则按式（11）所示规则在当前全局最优解附近进行随机扰动产生新解。

（5）再产生一个随机数，当该随机数小于Ai且，则蝙蝠个体i移往步骤（4）中新解所在位置。

（6）比较所有蝙蝠个体的适应度值，适应度值最小的蝙蝠个体位置即为当前最优解。

（7）重复步骤（3）～（6），直到满足最大迭代次数，得出最优蝙蝠个体位置，并根据映射关系得到最优的ELM隐含层输入权值矩阵和隐含层阈值矩阵。

输出：由步骤（7）中求得的最优的隐含层参数及步骤（2）中训练得到的输出权值构成的ELM网络模型。

测试阶段

输入：具有N″个实例的测试集。

（1）将训练阶段得到的隐含层输入权值和隐含层阈值代入式（5）求出测试集的隐含层输出矩阵H′。

（2）根据式（14）计算测试集的测试输出：

输出：测试集的分类结果。

5 实验分析

5.1 实验数据

为了测试蝙蝠算法优化极限学习机对TCD数据的分类性能，从山西省人民医院2017 年12 月的经颅多普勒超声报告中随机选取256例颅内动脉狭窄病人和512例正常人的TCD数据，每例数据包含左侧颈内动脉、右侧颈内动脉、左侧椎动脉和右侧椎动脉4个部位的收缩期最大流速（PSV）、舒张末期流速（EDV）、阻力指数（RI）和血管直径（R）等特征，特征数为16，数据标签来自山西省人民医院放射科医师的标注。

5.2 实验设计

首先对脑卒中TCD 特征数据进行归一化处理，然后将其中288 例作为训练集，288 例作为验证集，192 例作为测试集，训练BA-ELM 网络模型，测试模型对颅内动脉狭窄和正常人的分类准确率。其中训练集的作用是训练得到ELM的输出权值，验证集用来训练超参数，即ELM 网络模型中的隐含层输入权值和隐含层阈值。为了验证基于BA优化的ELM模型的优越性，设置了以下模型对比实验：BA 优化ELM、差分进化算法（Differential Evolution，DE）优化ELM、粒子群算法（Partical Swarm Optimization，PSO）优化ELM 和基本ELM。实验执行环境为Matlab R2016a，运行环境为Windows7家庭普通版。

经多次仿真实验，参数设置如下：蝙蝠种群大小取20，初始脉冲响度取1.6，初始脉冲发射速率取0.000 1，搜索脉冲频率范围取[0，2]，脉冲响度衰减系数设为0.9，脉冲发射速率的增强因子设为0.99，蝙蝠种群最大迭代次数为20。激活函数均取sigmoid 函数每种方法的实验结果都是20次独立运行的平均值。

5.3 实验结果和分析

表1 所示为各分类模型对TCD 数据的分类结果及其相应的隐含层神经元数和训练时间。可以看出，BA-ELM、DE-ELM 和PSO-ELM 的分类准确率比ELM分别提高了22.77 个百分点、20.84 个百分点和21.52 个百分点，所需隐含层神经元数却比ELM少，说明群智能算法不仅可以有效降低ELM 网络复杂度，同时可以有效提高ELM 的分类性能。另外，BA-ELM 算法的分类准确率最高，但所需隐含层神经元数最少，训练时间也比DE-ELM和PSO-ELM分类模型分别降低了7.90 s 和4.20 s。实验结果表明了BA-ELM 用于TCD 数据分类时的有效性。

而从原理上分析，DE 算法的全局搜索能力受种群多样性的影响，随着种群的进化，各个个体逐渐向最优个体靠近，个体间差异减小，种群多样性逐渐丧失，算法容易陷入局部最优[18]；PSO 算法前期收敛快，但由于所有粒子都飞往最优解方向，失去多样性，后期收敛速度降低，同时收敛精度到达一定程度后无法继续提高[19]；BA 算法的速度更新和位置更新公式与PSO 类似，但由于其采用了频率调整和参数控制策略，可以控制蝙蝠移动的速度和范围，使全局搜索更加高效，可以达到较高的收敛速度与收敛精度。因而在训练时间和分类准确率方面，BA-ELM均优于DE-ELM和PSO-ELM。

由表1 可知，ELM 的训练时间最短，这是因为群智能算法寻优的过程也占用一定的训练时间，而BA-ELM也仅需要1.56 s，但分类准确率从ELM的75.57%提高到98.34%，提高了22.77个百分点，表明了BA算法优化后的ELM的分类性能较经典的ELM有了显著提高，但训练时间的增加并不明显。

表1 TCD数据的分类结果及各算法隐含层神经元数和训练时间对比

为降低实验结果的偶然性，各算法均独立运行10次，以运行次数为横坐标，分类准确率为纵坐标画折线图，对BA-ELM、DE-ELM、PSO-ELM 和ELM 算法的稳定性进行了比较，实验结果如图3所示。与其他几种算法相比，BA-ELM 算法不仅可以取得最高的分类准确率，而且各次运行实验结果之间的波动最小，算法的稳定性最好。

图3 算法稳定性比较

综上，与其他群智能算法相比，BA-ELM 网络模型用于脑卒中TCD数据分类不但可以获得较好的分类效果，还可以降低训练模型所需的时间和网络结构的复杂度，且该算法具有较高的稳定性，与其他算法相比具有一定的优势。

6 结束语

本文针对ELM用于TCD数据分类时对隐含层输入权值和阈值参数选择敏感的缺点，提出一种基于BAELM 的脑卒中TCD 数据分类模型。实验结果表明，与其他智能算法优化ELM 的结果相比，BA-ELM 在分类准确率、计算效率及算法稳定性上，均优于其他群智能算法，从而验证了该算法的优越性。因此BA-ELM模型可以高效准确地分类TCD 数据，在脑卒中预测中具有重要的实际应用价值。实际的脑卒中TCD数据经常是不平衡的，本文算法以总体准确率为评价指标，其对不平衡率较高的数据集是否适用还需进一步的研究。下一步工作是研究不平衡率对分类器性能的影响，并改进算法使其适用于分类实际中的不平衡TCD数据集。