BSO-MCKD在高速列车齿轮箱轴承早期故障诊断中的应用*

朱 丹， 苏燕辰， 孙 琦， 龙 莹

(西南交通大学 机械工程学院, 成都 610031)

齿轮箱轴承是高速列车传动系统中的重要零部件之一，其故障或失效严重影响高速列车的平稳、安全及运行。随着高速列车运营速度的提升和线路的不断延伸，齿轮箱轴承的服役环境变得越加严酷恶劣，更易发生磨损、擦伤等损伤类故障。如果能在齿轮箱轴承早期故障阶段及时有效地检测出异常，会降低维修成本，并能有效避免故障发展到后期所带来的灾难性事故。因此，轴承早期故障检测极为重要，越早检测出轴承故障，越有利于高速列车的安全运行。

当轴承部件(外圈、内圈、滚动体和保持架)表面发生局部损伤时，会产生周期性冲击信号[1]，但早期故障冲击信号微弱且淹没于强烈的背景噪声中，因此探寻有效的微弱故障冲击成分提取方法是故障诊断领域的热点和难点。近年来，一些学者提出了很多有效的方法，如小波变换[2-3]，经验模式分解[4-5]，最小熵解卷积[6-7]等。其中小波变换方法在最优小波基的选取上还未有标准或成熟的选择方法；经验模式分解方法常出现过包络，欠包络和模态混叠等问题；最小熵解卷积方法的鲁棒性欠佳。

McDonald等[8]在MED的基础上提出了最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution，MCKD)的新方法，以相关峭度为评价标准，充分考虑故障冲击成分的周期性，突出信号中被强噪声所掩盖的连续脉冲，并将其应用到齿轮的故障检测中，取得了良好的效果。然而MCKD的滤波效果受到FIR滤波器阶数L、信号周期T和移位数M的严重影响。在MCKD的相关文献[9-11]中，参数M和L的选取大都通过经验来选择，缺乏相应参考标准，且参数T的选取也忽略了实际轴承故障频率与理论故障频率之间的差异，因此需要采用一种方法自适应的确定MCKD参数的最佳取值，使得MCKD方法取得较优效果。

提出采用天牛群优化算法(Beetle Swarm Optimization Algorithm，BSO)对MCKD的影响参数(L、T、M)进行寻优，实现自动寻找最佳参数的自适应MCKD算法，突出淹没在噪声中的连续冲击成分，然后根据解卷积信号中突出的连续脉冲成分的周期判断轴承状态，实现轴承故障的精确诊断。

1 基于BSO算法的MCKD方法

1.1 MCKD基本理论

MCKD的本质是寻找一个FIR滤波器，通过传感器输出信号x来恢复冲击信号y，从而达到抑制噪声和突出故障冲击成分的目的，即：

(1)

式中，f=[f1,f2,…,fL]T为滤波器的系数；L为滤波器的阶数。

MCKD是以相关峭度作为评定解卷积效果的指标，并将其作为求解最优结果的目标函数。对于任一信号yn，相关峭度定义为

(2)

式中，T为冲击信号周期；M为位移数。

MCKD算法的目标函数为

(3)

即求解方程

(4)

求解方程后得到的滤波器系数组合用矩阵形式可表示为

(5)

式中，

r=[0T2T…mT]

1.2 改进的MCKD

MCKD算法中，故障信号周期T、移位数M和滤波器阶数L3个参数决定了滤波效果。为避免人为主观因素对MCKD参数设置的影响，利用BSO算法自适应选取MCKD中的3个关键影响参数(T、L、M)。BSO[12]是一种新的全局优化算法，它将天牛觅食机制[13](BAS)和粒子群优化[11](Particle Swarm Optimization，PSO)紧密的结合起来，这两个部分的结合不仅加快了种群的迭代速度，而且降低了种群陷入局部最优的几率。

假设在D维空间中，由N只天牛组成种群X=(X1X2…XN)，其中第s只天牛代表一个D维的向量Xs=(Xs1Xs2…XsD)，天牛在D维空间中的速度为vs=(vs1vs2…vsD)，种群的全局极值和个体的局部极值分别为gbest和pbest。在粒子群算法的大框架下，由速度的更新(PSO)和步长的更新(BAS)共同决定天牛下一步的位置。个体位置更新公式：

(6)

式中：

w=wmax-(wmax-wmin)×k/n

式中：s=1,2 …N；c1,c2—天牛的学习因子，默认c1=c2=2；

k为当前迭代的次数；n为最大迭代数；

λ为[0,1]之间的常数，λ值越大，PSO算法更新方式占的比重越大，文中λ=0.5；

ξ为天牛位置的移动距离；，rand为介于[0,1]之间的随机数；

w为惯性因子，wmin和wmax分别表示w的最小值和最大值，文中wmin=0.4，wmax=0.9，使算法能够在进化开始时搜索更大的范围，并尽快找到最优解区域；

dk为k次迭代时质心到须的距离；c为常数；η为动态步长更新的系数，默认参数step1=0.4,step0=0.9；

在BSO优化过程中，需要确定一个适应度函数来衡量提取到的故障特征的丰富度。当轴承发生局部损伤时，通常在时域中出现周期性的脉冲序列，而在频谱中表现为突出幅值的故障特征频率和倍频成分。选取故障特征能量比[14](fault feature energy ratio，K)作为适应度函数来衡量所提取故障信号的优劣，K值越大表明所提故障特征成分越丰富，因此，K的最大化作为BSO寻优算法的最终目标。设滤波信号的包络谱幅值序列为X(j=1,2,…,M)，f为故障特征频率，则故障特征能量比为：

(7)

参数L、T和M的自适应选取过程：

(1)初始化BSO算法中的各项参数并确定优化过程中的适应度函数；

(2)以影响参数[T，L，M]的组合作为天牛，每只天牛对应一对影响参数，随机生成一定数量的参数组合作为天牛的初始位置，随机初始化每只天牛的移动速度；

(3)根据天牛的位置对信号做MCKD运算，并计算每只天牛相对应的适应度值

(4)计算每只天牛左右两须的位置，并计算左右两须的适应度值；

(5)比较所有适应度值大小并更新个体局部极值和种群全局极值；

(6)利用式(6)更新粒子的速度和位置；

(7)循环迭代，转至步骤(3)，直至迭代数为最大设定值，输出最大适应度值对应的天牛位置。

2 诊断流程

利用MCKD算法处理低信噪比的轴承故障信号时，如何筛选出MCKD影响参数的最佳组合，增大信噪比，且最大程度突出信号中的规律性冲击成分是故障诊断的关键所在。为了实现影响参数组合的最佳自适应选择，利用BSO算法并行搜寻MCKD算法的影响参数(L、T、M)，然后设置最佳参数对原始信号进行MCKD滤波，在解卷积信号的时域波形中突出由故障引起的周期性冲击特征，并依据该特征的周期判断故障的位置。具体诊断流程如下所述：

(1)设定BSO算法中各项参数并搜索MCKD算法的3个影响参数。考虑到轴承理论故障频率f与实际故障频率之间的差异，T参数的初始化范围为[fs/f-5,fs/f+5],fs为采样频率；L和M参数的初始化范围分别为[10，500]和[1，8]；天牛群规模N为30，迭代次数n为30。

(2)BSO优化完成后会得到一组最优参数组合[L，T，M]，设定MCKD算法的滤波器阶数L、解卷积周期T和移位数M，并利用参数优化后的MCKD算法对故障信号进行解卷积处理。

(3)根据以上获得的解卷积时域信号中由故障激发的连续性脉冲的周期来判断轴承当前状态。

3 轴承全寿命周期的加速度试验

为了验证文中方法在滚动轴承早期故障诊断上的可行性和有效性，选取NSFI/UCR智能维护系统中心的滚动轴承全寿命周期的加速度试验数据[15]进行分析。试验台布局如图1所示，试验转轴上同时装有4个相同的ZA-2215双列圆柱轴承，轴承参数见表1，转速为2 000 r/min。每个轴承的水平和垂直方向各布置一个加速度传感器来采集轴承的振动信号，采样频率fs=20 kHz。

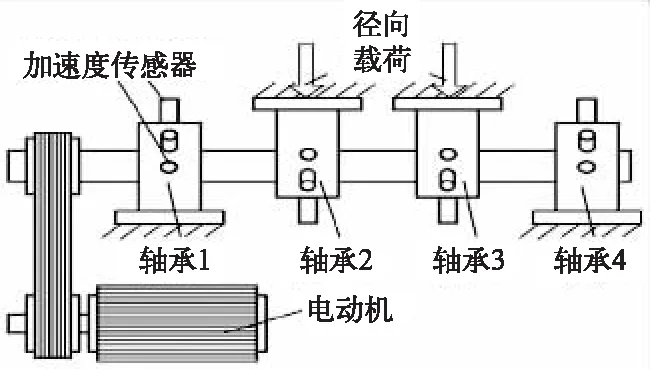
图1 试验台示意图

轴承节径D/mm滚动体直径d/mm滚动体个数Z接触角α/弧度71.58.4160.264 8

根据轴承参数计算得到轴承外圈理论故障特征频率fo=236.4 Hz，那么周期性冲击间隔为0.004 23 s。从图2所示的轴承原始振动信号中看不到明显的周期冲击成分。为了准确判断轴承是否发生了故障，利用文中提出的基于BSO优化的MCKD算法处理轴承的原始振动信号，结果如图3和图4所示。图3为轴承故障特征能量比随迭代数进化的关系曲线，当迭代至第10代时，得到最大的特征能量比5.026 5，BSO算法寻优得到的滤波器阶数、解卷积周期和移位数的最佳组合为[430,86.57,6]。从图4(a)中能清楚的看出间隔为0.004 28 s 的周期性冲击成分，与轴承外圈理论故障频率236.4 Hz吻合，且图4(b)中轴承外圈故障特征频率fo及其倍频处幅值突出，谱线清晰，由此可以确定轴承外圈发生了局部损伤故障，需要及时进行维修，保证生产持续进行。

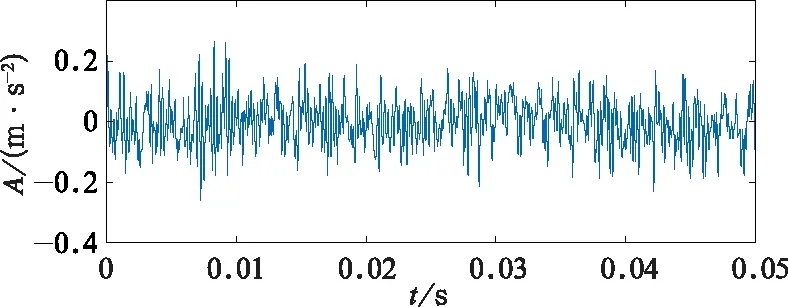
图2 轴承原始振动信号时域波形

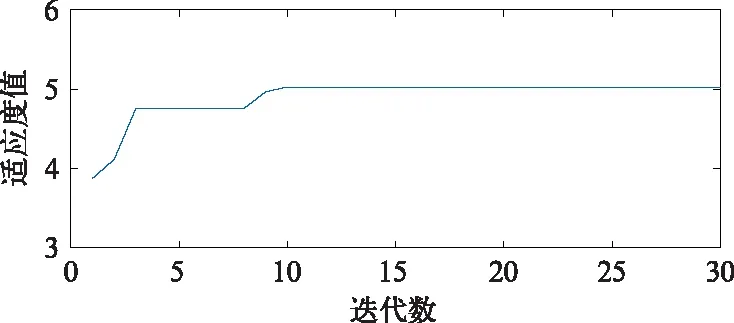
图3 故障特征能量比随迭代数进化的关系曲线

为了进行对比分析，利用互补集合经验模态分解方法对轴承的原始振动信号进行处理，结果如图5所示。图5(a)中第2个模态分量IMF2有一定的冲击性，但是冲击间隔不明显，不易于轴承故障判别，且图5(b)包络谱中也无法识别轴承故障特征频率，由此可以说明CEEMD诊断效果不如文中提出方法。

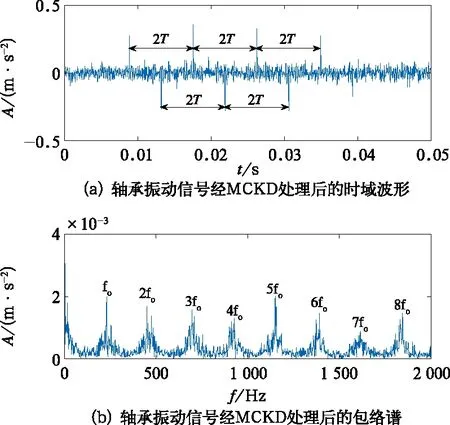
图4 轴承振动信号经MCKD处理后的时域图和包络谱

图5 轴承振动信号经CEEMD处理后的时域图和包络谱

4 高速列车齿轮箱轴承故障试验

为了进一步说明文中方法的有效性，使用来自图6的某型号高速列车的齿轮箱轴承台架试验数据进行验证。试验轴承型号为R70的圆锥滚子轴承，轴承参数如表2所示。在轴承滚动体上加工宽和深都为0.03 mm的划痕来模拟轴承滚动体故障，设定的采样频率为10 kHz，电机转速为2 396 r/min，计算出轴承滚动体的故障特征频率fb=209 Hz，那么周期性冲击间隔为0.004 78 s。

图6 齿轮箱轴承试验台

表2 R70轴承结构参数

轴承原始振动信号时域波形如图7所示，从时域波形中可以看到一定的周期冲击成分，但是噪声成分比较大，并不能准确判断轴承故障。为了充分确定轴承故障的发生，利用文中提出的基于BSO优化的自适应MCKD算法对高速列车齿轮箱轴承故障信号进行分析，结果如图8和图9所示。图8为轴承故障特征能量比随迭代数进化的关系曲线，在第15代时，特征能量比最大为6.205 0，BSO算法寻优得到的滤波器阶数、解卷积周期和移位数的最佳组合为[499,46.8,7]。从图9(a)中可以发现振动原始信号经参数优化的MCKD算法处理后，获得的解卷积信号中脉冲成分十分突出，且具有明显规律，0.004 72 s的周期与理论上的轴承滚动体故障特征频率209 Hz相符，图9(b)中轴承滚动体故障特征频率fb及其倍频处幅值突出，所以可以断定高速列车齿轮箱轴承的滚动体发生了故障，应及时进行有计划的检查和维修。

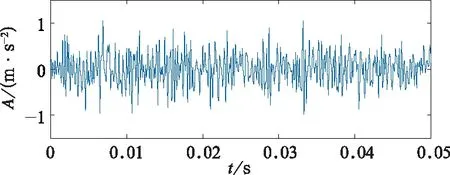
图7 轴承振动信号的时域波形

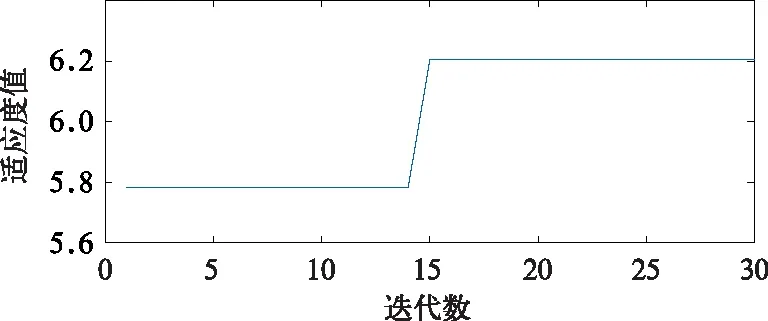
图8 故障特征能量比随迭代数进化的关系曲线

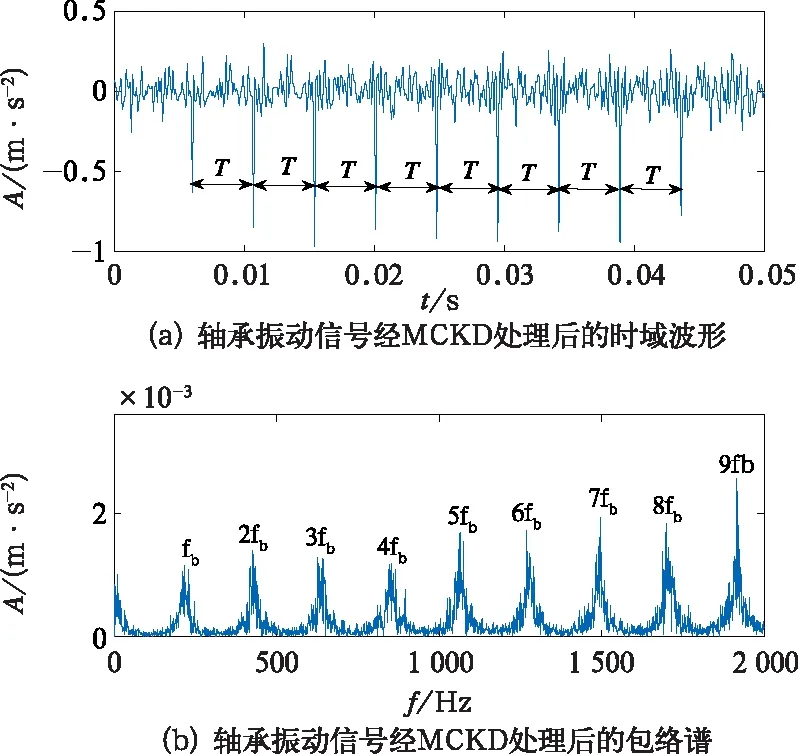
图9 轴承振动信号经MCKD处理后的时域图和包络谱

为了对比分析，利用文献[6]中基于最小熵解卷积的轴承微弱故障特征提取方法对轴承原始振动信号进行分析，得到的结果如图10所示。用该方法能提取到一定的冲击成分，但是相较于文中方法，其提取结果中仍含有较强的噪声，故障冲击特征不是很明显。

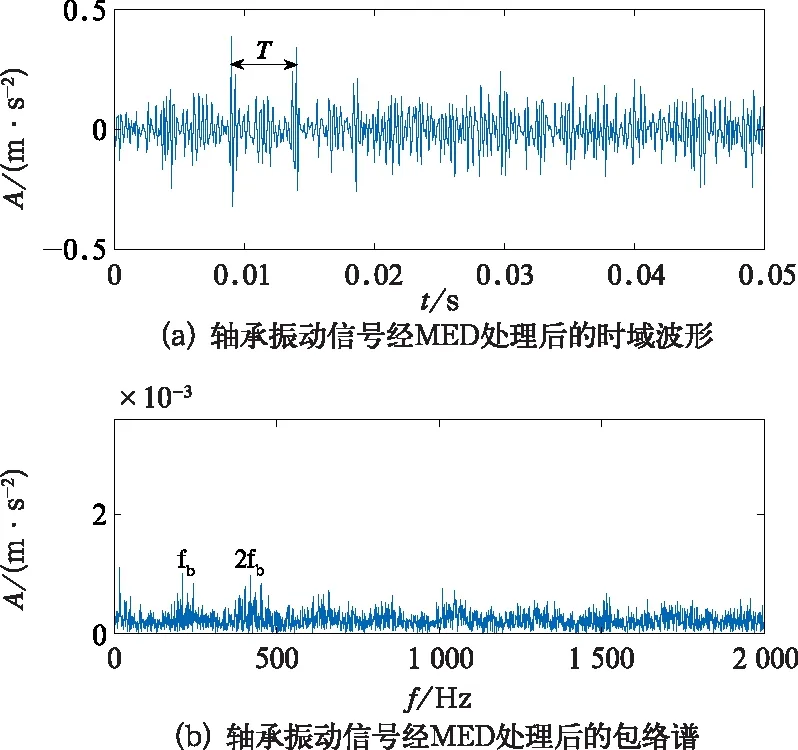
图10 轴承振动信号经MED处理后的时域图和包络谱

5 结束语

(1)基于BSO改进的MCKD方法能够自动搜寻最优滤波器阶数、冲击信号周期以及移位数，使MCKD方法具有自适应性且能够有效的提取轴承原始信号中被噪声掩盖的冲击成分，实现对高速列车齿轮箱轴承早期故障的准确诊断。

(2)在轴承早期故障的检测及诊断上，基于BSO改进的自适应MCKD方法的诊断效果要优于CEEMD和MED方法，且该方法为高速列车齿轮箱轴承的早期故障诊断提供了一种新的手段。