遵循波利亚“解题表”,深挖题目内在价值
2020-05-19麦少凤
麦少凤

[摘 要] 教师如果认为“题目简单”而不太重视课本习题,则易陷入“为做题而做题”的误区. 课本中会有一些“小题目”,教师借助波利亚的“怎样解题表”,可以帮助学生更快更有效地找到解决问题的切入点和难点的突破点,还可以让自己更深入地挖掘题目本身的内在价值,让“小题目”产生“大发现”的美妙变化,有利于师生的解题思维提升.
[关键词] 波利亚“解题表”;内在价值;通性通法
问题缘起:一道课本习题
案例 如图1,在正方形ABCD中,M是BC的中点,MN⊥MA,CN平分∠DCE,E为BC的延长线上一点. 求证:MA=MN.
上述案例是人教版教材八下的一道课本习题,这是很经典的一道习题,很多地方的中考题或期末考试题都喜欢以这道题为母版进行改編,而且经久不衰. 由此可见,这道题蕴含着丰富的内在价值,值得我们对它进行深度探究. 下文,我们将遵循波利亚“解题表”的四部曲,深挖该题的内在价值,并以此为契机,引导读者触类旁通、举一反三.
众所周知,学生解题时遇到的最大困难是,即使他们已掌握了扎实的基础知识(数学的基本概念、公式、定理、方法)和基本技能,也可以运用它们去解决一些问题,但面对陌生的问题时,他们却不知如何下手,宛如“老虎吃天,无从下口”. 近年来,广州的中考题每年都会呈现好几道这样“宛如天降”的压轴题,让广大考生束手无策,根本不知从何下手. 广州中考数据显示,分数段在130-150的考生占比:2017年为5.52%,2018年为2.13%. 因此,对于广大广州考生来说,中考数学拿高分是相当困难的事情. 造成压轴题难以成功突破的原因虽然有很多,但最重要的可能是以下两方面:一是缺少解题的基本思想方法,二是缺少指导自己理解题意的基本方法. 而波利亚的“解题表”,虽然没有为我们提供一个万能的解题方法,但却可以引导我们更好地理解题意,更容易找到解题的思路,同时也可以引导我们更进一步地思考题目的内在意义,达到解一题,懂一类,甚至触类旁通的效果.
波利亚的“怎样解题表”是针对“怎样解题”“怎样学会解题”等问题,教师把“解题中典型、有用的智力活动”,按照学生解决问题时思维的自然过程分为四个阶段,即弄清问题、拟定计划、实现计划、回顾,描绘出解题理论的一个总体轮廓,也组成了一个完整的解题系统.
解题策略
(一)弄清问题
(1)你要求证什么?
题目要求证的是MA=MN.
(2)你有哪些条件?包括外显条件、内含条件或隐含条件?
一方面是题目给出的正方形ABCD中,M是BC的中点,MN⊥MA,CN平分∠DCE,另一方面是由这些已知条件可以直接推出的BM=CM,∠BAM=∠EMN,∠MCN=135°.
(二)拟定计划
1. 题目类型识别
当我们着手解答一道习题的时候,第一件事就是要识别题目类型,这个过程也叫模式识别. 倘若识别了习题的类型,在多数情况下,我们就能得到解题的思路,因为有很多类型的习题都会有它们对应的解题法则或解题方法.
例如,若要证明线段相等,最常规的思路是通过证明这两条边所在的三角形全等;如果这两条线段在同一个三角形,则可以借助等角对等边证明两腰相等;如果在直角三角形背景下,还可以借助三角函数,也可以通过勾股定理证明这两条线段的长度相等. 这是证明线段相等的一般思路,当然,最常规、最基础、最具一般性的方法,肯定是证明三角形全等了.
2. 辅助问题与形成计划
有很多习题,尽管能够识别出对应的类型,但通常不能直接套用在待解决的问题中,又或者是问题本身的类型并不容易被识别或根本是自身不熟悉或费解的,此时就需要设置“桥梁”,以完成从未知到已知的转化,而这些所谓的“桥梁”就是指辅助问题了.
从题目图形可知,AM所在的三角形是Rt△ABM,而MN所在的三角形是钝角△MCN,这两个三角形不可能全等.
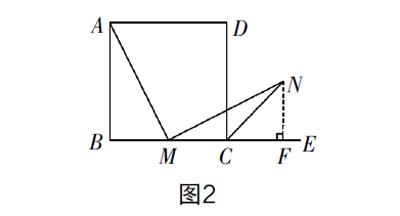
辅助问题 那还能否通过证全等的方法证明结论?可以,但必须添加辅助线. 那应该怎样添加?要么利用MN构造一个直角三角形与Rt△ABM全等,要么利用AM构造一个含135°的钝角三角形与△MCN全等. 然而,方案一中的构造Rt△MFN,却不够条件证明Rt△MFN与 Rt△ABM全等(如图2).
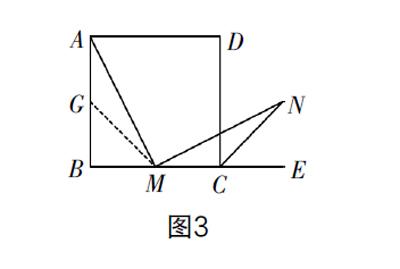
形成计划 改用方案二,在Rt△ABM的AB边上通过截取BG=BM构造△AGM,再证明△AGM与△MCN全等(如图3). 而该方案的难点是怎样才能想到在AB边上通过截取BG=BM构造△AGM与△MCN全等,思考的依据是:由条件可知,∠BAM=∠EMN,∠MCN=135°,因此构造的新三角形必须含有135°角,而135°角会让人联想到45°角,而45°角就不难让人联想到等腰直角三角形,难点可由此进行突破.
(三)实现计划
证法1:如图3,在AB上截取BG=BM,
因为四边形ABCD为正方形,点M为BC的中点,
所以BM=CM=BG=AG,∠BGM=BMG=45°.
又CN平分∠DCE,
所以∠NCE=45°,∠AGM=∠MCN=135°.
又MN⊥MA,
所以∠BAM+∠AMB=90°,∠CMN+∠AMB=90°,
所以∠BAM=∠CMN,
所以△AGM?艿△MCN(ASA),
所以MA=MN.
(四)回顾
1. 检验与拓展
正面检验每一步的推理是否有效,计算是否准确,确认无误后,再思考除了上述方法外,还能否用别的方法证明这个结论?站在中考复习的维度上,要证明线段相等,在具备某些特定条件的前提下,本案例还可以借助三角函数或构建坐标系求解.
证法2:借助三角函数证明MA=MN. (初三适用)
如图2,由于∠BAM=∠EMN,所以tan∠BAM=tan∠EMN,设NF=x,AB=2a(或AB=2也行),由 = = ,解得x=a,从而可证MA=MN.
证法3:通过构建直角坐标系,求出N点坐标.
如图4,构建直角坐标系,设AB=2,N点坐标为(1+a,a),先求出线段AM的解析式,再由MN⊥MA,k ·k =-1,求出线段MN的解析式,将N点坐标代入,即可求出a的值,从而求出AM与MN的长度,进而得证.
2. 推广与变式
“推广”指将题目及其解法的本质推广到类似的情境中;“變式”指保持题目或解法中的一些成分不变,改变某个或某些成分,产生不同类型的变式题.
变式:本案例中的M点是线段BC的中点,具有特殊性,倘若改变M点的位置,令点M为直线BC上任意一点,则题目的结论还会成立吗?
分类讨论:①当点M在线段BC上(对应图5);②当点M在线段BC的延长线上(对应图6);③当点M在线段BC的反向延长线上(对应图7). 经研究发现,改变点M的位置,变成上述三种情况时,题目的结论仍然成立,证明的思路与上文的证法1相同,但用证法2和证法3却不可行. 由此可见,证法1才是通性通法,具有一般性,而证法2和证法3具有特殊性,在题目具备特殊条件时可行.
我们是否会得到更一般性的结论呢?
思考1:把题目中的“正方形ABCD”改为“等边△ABC”,把“M是BC的中点”改为“点M为直线BC上异于B,C的任意一点”,点N是∠ACE的角平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?
结论1:结论成立. 如图7、图8、图9所示,证明思路与上述变式相同.
思考2:如果把原题目中的“正方形ABCD”改为“正n边形ABCDE…”,当∠AMN= 时,结论AM=MN是否还成立?
结论2:结论仍然成立,只是要借助高中会学到的数学归纳法才能证明. 但作为初中生,教师可以引导学生去猜想和发现(无须证明)这个结论,也是非常有价值的. 另外,也可以把本题改成一道填空题,让学生猜想当∠AMN=______°时,结论AM=MN仍然成立(无须证明).
教学启示
(一)启示之一:“通式通法”显价值
章建跃博士反复强调:一线数学教师一定要注重“通性通法”的教学,而所谓的“通性”就是指概念所反映的数学基本性质;“通法”则是指概念所蕴含的思想方法. 在教学中,注重数学的基础知识、基本性质及其所蕴含的数学思想方法,才是追求数学教学的“长期利益”. 而在解题教学中,“通法”是指最常见、最基本的解题模式. 在本案例中,我们会发现通过作辅助线构造△AGM与△MCN全等是解决这道题的通法,具有一般性和普适性,最重要的是当改变题目条件时,这种方法同样适用,而其他的很多方法已经不适用了,这就是大巧若拙的“通性通法”的价值所在了. 因此,在解题教学中,我们要使学生逐步养成从基本概念、基本原理及其联系性出发思考和解决问题的习惯,追求解决问题的“通性通法”才是发展学生思维能力的正道.
(二)启示之二:“借题发挥”助升华
“借题发挥”来解决问题,就是借助解决某个简单的问题来解决更难或隐藏更深的问题,以彰显这个问题的价值. 如果我们只满足于原题目,就发现不了“当改变点M的位置”或“改变图形背景”时,问题的结论仍然成立这个一般性的问题,因而也就更难发现原来这个问题还可以推广到一个正多边形中去这个更具一般性的命题,这样这道题就失去了它本该有的内部价值了,这对于学生来说是非常大的损失. 因此,在解题的过程中,只要我们坚持把握问题的价值,坚持厘清问题本质,坚持运用变式问题的眼光,借发挥已解决过的习题的价值来解决更深入的问题,就一定会更有收获.
(三)启示之三:“回归课本” 是正道
波利亚指出:“一个有责任心的教师与其穷于应付烦琐的数学内容和过量的题目,还不如适当选择某些有意义但又不太复杂的题目去帮助学生发掘题目的各个方面,在指导学生解 题的过程中,提高他们的才智与推理能力. ”本案例的题目来源于课本的习题,题目本身难度不算太大,但学生在没有提示的前提下答题,情况并不理想. 这只是浩瀚题海中一道很普通的题目,但深挖后却发现小题目蕴含大学问. 此外,我们的学生做了很多题目,可是一到真正的大考,我们所有的尖子生几乎全部沦陷;更离谱的是,还有不少教师认为课本的题目太简单,没有可做性,教学全程居然都不使用课本……其实,从上述案例及其变式延伸中我们可以看出,学生的解题思维没有培养起来不是因为课本的题目不够好、不够多,而恰好是因为我们普遍没有重视课本,没有认真对待教材,不愿意也不用心去帮助学生深挖课本习题的各个方面及其内在价值,只是纯粹地为做题而做题. 因此,让我们的教学回归课本,重质减量,选好题讲好题,注重思维培养,才是数学教学之正道也.
