基于现场实测的大跨钢桁悬索桥疲劳可靠度分析

韩 艳，李 凯，孙一婵，蔡春声

(1. 长沙理工大学 土木工程学院，湖南 长沙 410114；2. 路易斯安那州立大学 土木与环境工程系，美国 路易斯安那州，巴吞鲁日 70803)

0 引言

钢桁桥因跨越能力强、施工方便、外形优美、整体性好被广泛应用于大跨度桥梁，尤其是大跨度悬索桥。在长期的车辆荷载和风荷载作用下，钢桁架主梁各杆件尤其是杆件的各个连接部位将长期处于累积疲劳损伤的状态[1-2]，进而影响桁架主梁结构的长期安全运营。因此，对大跨度钢桁架悬索桥关键构件处的细节进行疲劳可靠度评估显得极为重要。

以往对钢桥疲劳的研究大多基于疲劳应力谱，因此，首先需要对处于正常运营期的大桥车流情况进行调查统计并分析，再通过确定不同车型荷载参数建立车辆荷载谱，最后得到只能反映大桥整体的车载特征，因此得到的局部应力分析结果将会在较大程度上与实际情况不符[3-5]。为了更好地掌控大桥的服役情况，结构健康监测系统应运而生，目前已广泛地在大跨度桥梁领域使用[6-8]，应变时程可直接通过监测系统得到，用于疲劳分析的疲劳应力谱可由雨流计数法获得，随后便可对桥梁钢结构构件细节进行疲劳累积损伤及可靠度评估研究[9-10]。但桥梁健康监测系统经济投入成本很大，而且以往基于现场实测的研究往往针对大跨度钢箱梁桥[11-14]，基于现场监测数据研究大跨度钢桁梁悬索桥关键构件的疲劳可靠度较少。

为节约成本，针对大跨度钢桁梁悬索桥，首先采用ANSYS软件建立了大桥的壳-梁混合单元空间桁架主梁有限元模型，随后通过分析确定了大桥的关键构件及关键点。针对关键构件的关键点，进行为期6 d的应变实时监测，通过对实测数据的预处理，获得了比较准确的应力响应，然后对于所测关键构件的关键点运用核密度估计法建立基于小子样的疲劳荷载谱概率分布模型，研究大桥所测关键构件关键点的疲劳可靠度，为大桥的安全运营提供保障。

1 有限元建模及关键截面确定

本研究以某大跨度钢桁架悬索桥为工程背景，其主跨为1 176 m，主缆采用(242+1 176+116)m的孔跨布置方式。加劲梁选用梁高为7.5 m且桁架节间距为7.25 m的钢桁梁。桥面行车道系钢纵梁与混凝土桥面板相结合，钢纵梁与主桁上横梁之间选用橡胶支座支承方式，左右两幅桥面行车道布置方式为有间距分离布置。

在ANSYS软件平台建立了该大跨悬索桥的有限元模型，节点与单元个数分别为84 085个与76 846个。模型中采用beam188梁单元来模拟加劲梁所有构件以及索塔部分，吊杆以及主缆均为Link10杆单元；为了能最大程度上接近大桥的真实情况，针对钢-混组合桥面系采用壳-梁单元混合有限元模型，并通过MPC方法使得Shell63单元(桥面板)与Beam188单元(钢纵梁)连接形式为耦合连接。壳-梁单元混合有限元模型如图1所示。

图1 壳-梁单元混合有限元模型Fig.1 FE model of shell-beam hybrid elements

移动车辆荷载作用下大桥各构件的应力响应可通过ANSYS瞬态计算实现，进一步对应力结果进行统计分析就能获得大桥在随机车流荷载作用下的关键节点位置。为了能够实现车辆荷载的每一荷载步均作用在Shell63单元(桥面板)的节点上，根据桥面车辆的移动速度以及时间步长确定了建模时Shell63单元需采用的横桥向与顺桥向的尺寸[15]，利用节点集中力荷载来代替移动车辆。从应力计算结果可知，首先，杆件的轴向应力与杆件的第一主应力在数值上相差不大，这说明大桥的钢桁架杆件在车辆荷载作用下以承受轴向的拉压应力为主，这也跟现实情况相吻合；其次，大桥跨中横桥向下弦杆为加劲梁钢桁架轴向应力幅值较大的构件，在此基础上对跨中的钢桁架进行详细划分并进行计算分析；最后基于计算的结果确定了大桥关键部位，如图2所示，其中加粗部分指最大应力关键点与关键位置。

图2 最大应力位置Fig.2 Position of maximum stress

2 关键截面应变实时监测及数据分析处理

2.1 应变实时监测

根据上一节大桥有限元模型计算结果，综合考虑设备实际情况和试验的经济有效性，本研究选取靠近跨中的68#截面作为测试断面，如图2所示。选取该断面的多个关键构件，在关键构件的关键点布置应变传感器，如图3所示。在斜腹杆和中间直腹杆底部位置沿杆件轴向各布置一个单向应变片，在中间下弦杆的中间位置的上下表面各布置了一个多向应变花，在中间下弦杆的两端上表面各布置了一个沿轴向的单向应变片。为获得大桥疲劳荷载信息，采用智能信号动态采集仪在桥址现场进行了为期6 d的实桥数据采集。

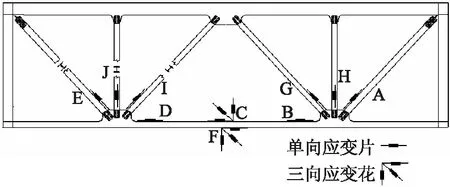
图3 测点布置示意图Fig.3 Layout of measuring points

应力幅大小以及循环次数是桥梁产生疲劳损伤的两个决定性的影响因素，而应力幅的大小又取决于车辆荷载的变化。由于在测试过程的环境比较复杂，风与温度等自然条件将会对测试结果产生影响，得到的测试结果中还包括了大量的噪音成分，因此，实测数据将会不理想，与实际情况存在偏差。为了确保结果的真实性与可行性，尽量选择无风的天气进行测试。另外，进行疲劳分析前，首先采用趋势平均法消除了温差对细节所测应力时程的影响，其中测点E消除温差影响后的应力响应时程如图4所示。

图4 测点E消除温度影响后的应力时程Fig.4 Stress time history of point E after erasing influence of temperature

图5(a)～(e)为车辆通过68#截面时所测关键点的应力时程，其中以桥面中心线为分界线，与车辆在同一侧的杆件定义为同侧杆件，不在同一侧的杆件定义为不同侧杆件。其中由图5(a)可以发现，当车辆从外侧加厚斜杆上部桥面经过时，同侧杆件和不同侧杆件都承受拉应力，其中与行驶车辆处相同侧的杆件所受拉应力要明显大于不同侧的。从图5(b)、(d)和(e)可以发现，对于主横桁架的直腹杆、下弦杆以及斜腹杆，当车辆从同侧经过时受压应力，当车辆从异侧驶过时受拉应力。由图5(c)可知，当车辆经过时，主横桁架下弦杆上下表面的动态应力幅值较小，且行驶车辆的方向对其影响微弱。疲劳损伤的程度主要取决于应力幅值的大小与应力循环次数，从实际监测中发现E测点侧的车流量明显要多于A测点侧的车流量，另外从图5中可以看出，外侧加厚斜杆的应力幅值比其他杆件相对要大些，因此基于以上两点本研究选取测点E进行疲劳累计损伤计算和寿命评估。

图5 某时间段内各测点应力变化情况Fig.5 Change of stress of each measuring point in a certain time period

2.2 数据分析处理

应力时程能反应所测杆件的应力大小与时间的关系，无法直接得到各应力幅的作用次数，通过雨流计数法对2017年6月12日测点E的应力时程进行统计处理得到的雨流计数直方图如图6所示。其中应力幅值2 MPa以下的循环次数最多，且其数量级远大于2 MPa以上的应力幅值，如表1所示。另外，对所测的应力时程进行疲劳累积损伤分析，得到的疲劳损伤直方图如图7所示。通过与图6进行对比可知，应力幅值低于2 MPa的应力循环产生的累积疲劳损伤极小。因此，文中忽略幅值低于2 MPa的应力循环，以提高计算效率，图8给出了经过处理后的测点E的雨流直方图。

图6 雨流计数直方图 (2017年6月12日测点E)Fig.6 Rain flow count histogram of Point E on June 12, 2017

采用以上数据处理方法对测点E所测得的2017年6月12日到6月17日的应力时程进行处理，得到了如图9所示的疲劳应力谱。

表1 测点E 2017年6月12日疲劳荷载Tab.1 Fatigue loads of Point E on June 12, 2017

图7 测点E疲劳损伤直方图(2017年6月12日)Fig.7 Fatigue damage histogram of Point E on June 12, 2017

图8 处理后的测点E雨流计数直方图(2017年6月12日)Fig.8 Processed rain flow count histogram of Point E on June 12, 2017

从图9中可以看出，连续6 d的疲劳应力谱非常相似，而且均分别在2，6 MPa和12 MPa应力范围处出现了波峰，2 MPa应力范围对应的循环次数最多，6 MPa的次之，12 MPa的相对较少。这一变化规律与钢箱梁的疲劳应力谱的变化规律有所不同，这可能是由于本研究的大桥是钢桁梁，与钢箱梁的结构受力不同所致。

3 基于实测数据的关键构件疲劳可靠度分析

3.1 疲劳极限状态方程

基于Palmgren-Miner线性累积损伤准则，结构的疲劳累积损伤定义为[16-17]：

(1)

式中，ni与Ni分别指应力幅值为Si对应的作用次数与常幅S-N曲线中应力幅值Si的疲劳寿命；Seq为等效应力幅值；Nd为等效应力幅值Seq对应的循环次数。在随机车辆荷载作用下构件细节处的应力循环具备高周变幅的特点，基于疲劳损伤等价的原则可获得等幅应力循环的等效应力幅值Seq。因此，基于欧洲规范Eurocode 3[18]，等效应力幅值Seq可定义为[19]：

图9 测点E的疲劳应力谱Fig.9 Fatigue stress spectrum of Point E

(2)

(3)

式中，Si和Sj分别为应力谱中大于常幅疲劳极限ΔσD的应力幅和小于常幅疲劳极限ΔσD的应力幅；ni和nj分别为应力谱中大于常幅疲劳极限ΔσD的应力幅所对应的循环次数与小于ΔσD对应的循环次数；KC和KD分别为应力幅大于和小于ΔσD的疲劳强度系数，分别表示为：

(4)

式中，ΔσC为构件细节类型；ΔσD为相应细节类型对应的常幅疲劳极限值。

大桥关键构件在随机车辆荷载作用下发生疲劳破坏是损伤长期累积的结果，由此可建立关键构件的疲劳损伤极限状态方程，表达式为：

g(X)=Df-D，

(5)

式中，Df为临界损伤；D为结构使用期内的随机车流荷载作用下的累积疲劳损伤值。在Miner线性累积损伤理论把1定为结构的临界损伤值，但是众多工程实例表明结构发生破坏时的Df具有一定的随机性，并非一个固定值；X为选取的随机变量。由于目前大跨度桥梁一般选用100 a的设计基准期，本研究中的等效应力幅Seq以及与之相对应的循环次数Nd代表的是一天的情况，每天产生的疲劳损伤可以由式(1)计算得到，每天的疲劳损伤乘以365 d再乘以桥梁服役年数n可得桥梁服役期所产生的疲劳损伤，那么大桥关键构件的疲劳损伤极限状态方程表示为：

(6)

当关键构件关键点发生疲劳破坏时，实际的累积疲劳损伤将会大于临界损伤，即g(X)<0，在役大桥重要构件的疲劳可靠度指标可表示为：

β=Φ-1(1-Pf)=-Φ-1(Pf)，

(7)

式中，Pf为失效概率，且Pf=P(g(X)<0)；Φ-1(·)为标准正态分布的逆函数。

3.2 极限状态方程随机变量的概率特征分析

本研究选极限状态方程中的临界损伤Df、日循环次数Nd、日等效应力幅Seq以及材料性能参数KD为随机变量，下面将详细介绍各随机变量的概率分布特征。

本研究假设临界损伤Df服从均值为1，变异系数为0.3的对数正态分布[20]。本研究采用欧洲规范Eurocode 3的疲劳强度S-N曲线，细节编号为90，假设疲劳强度系数KD服从对数正态分布，均值为6.26×1015，变异系数为0.45。

文中关键点的应力测试只有6 d，样本数量较少，为此通过核密度估计方法来构建日等效应力幅Seq基于小样本的概率分布模型以更为准确地获得其概率分布特征[21]。节假日、天气情况都会影响每天的车流量和车辆类型分布进而影响日等效应力幅Seq的概率分布，因此需将样本范围扩大，其边界范围[a，b]定义为：

(8)

(9)

式中，N为样本的个数，样本中的最大值和最小值分别用Xmax和Xmin表示。若样本外的可能数据不落在边界范围的概率为p，则其表达式为

p=P[x(N+k)∉[a,b]]，

(10)

式中，k大于0。

若样本以外可能的数据与样本都服从某个独立分布fx(x)，则产生在边界范围内的数据的概率为：

(11)

那么所得样本的发生概率为qN，当给定一个置信区间(1-α)时，将建立更加趋于真实的概率模型。若显著性水平α=qN，那么

P(α，N)=1-α1/N。

(12)

文中显著性水平取0.01。

以局部正态分布和最大值熵原理为先验条件，利用核密度估计表示应力循环次数与等效应力Seq的概率密度：

(13)

(14)

式中，σ为标准差，可由式(13)和式(14)确定。

由于样本数据只有约一周的车流荷载信息，因此相对地扩大样本的数量以获得更多样、分布范围更广的等效应力值，将每一天的应力时程分成6个相等的时间段，那么式(2)中Seq可表示为：

式中，Seq1至Seq6为相应的时段对应的等效应力值。

基于以上通过核密度估计理论推导的公式，可得一天中6个时间段Seq的标准差为0.553 1，0.524 4，0.715 3，0.868 6，0.498 4，0.441 3，日应力循环次数标准差为428。图10和图11分别为第4时间段的Seq概率密度函数和概率分布函数，图12和图13分别为全天的应力循环次数的概率密度函数和概率分布函数。

图10 等效应力概率密度函数Fig.10 Probability density function of equivalent stress

图11 等效应力概率分布函数Fig.11 Probability distribution function of equivalent stress

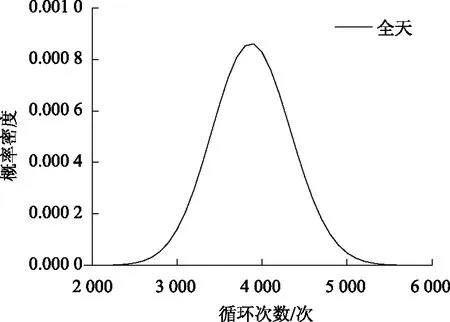
图12 全天循环次数概率密度函数Fig.12 Probability density function of daily cycle numbers

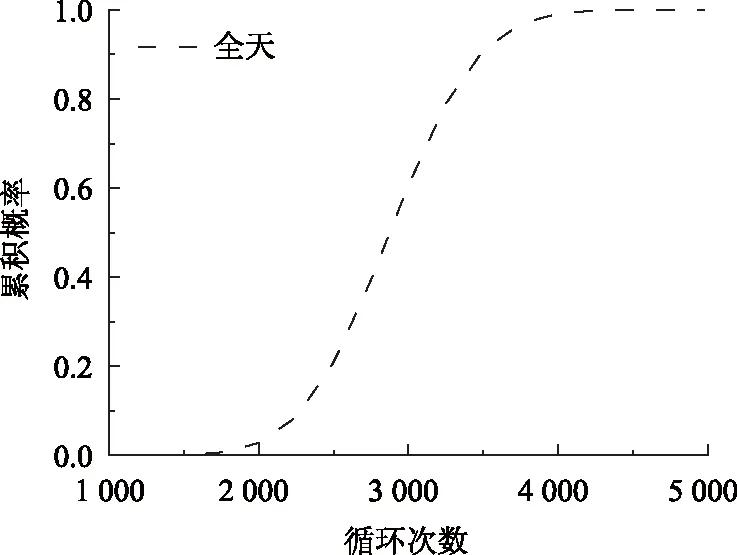
图13 全天循环次数概率分布函数Fig.13 Probability distribution function of daily cycle numbers

3.3 疲劳可靠度分析

目前结构可靠度分析方法通常有一次二阶矩方法(包括中心点法、验算点法和最优化方法)和Monte-Carlo方法等。Monte-Carlo方法的特点是不要求把随机变量当量正态化，也无需将随机变量当量正态化，极限状态函数的非线性程度与整个模拟过程是没有关系的，收敛速度也不受随机变量维数的影响，可以通过大量重复仿真计算使得可靠度的计算结果接近准确值。因此采用Monte-Carlo方法对关键构件的可靠度进行分析，整体计算流程如图14所示。

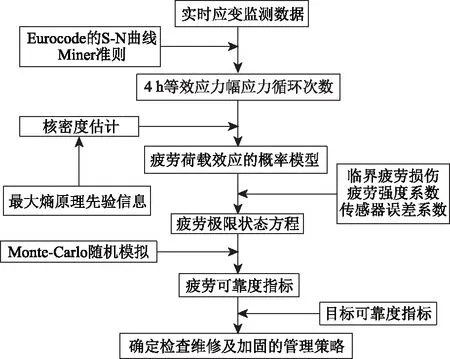
图14 疲劳可靠度分析流程Fig.14 Flowchart of fatigue reliability analysis

图15 外侧斜腹杆时变疲劳可靠度曲线Fig.15 Curves of fatigue reliability vs. service time for outside oblique web member

该大跨悬索桥桁架主梁构件细节的时变疲劳可靠度指标曲线可依据式(6)和式(7)利用Monte-Carlo法获得，另通过设置两种车流量的线性增长系数2%和5%[18]以研究车流增长系数对疲劳可靠度的影响。图15为外侧斜腹杆测点E处的时变疲劳可靠度指标曲线，图中目标疲劳可靠度指标取2。

从图15可知疲劳可靠度指标随着服役年限的增长而不断降低进而增大结构疲劳失效的概率；车流量的增长会显著降低构件在服役期的疲劳可靠度， 当车流量增长系数为0时，构件的疲劳寿命远大于350 a；当车流量增长系数为2%时，构件的疲劳寿命降为250 a左右；当车流量增长系数为5%时，构件的疲劳寿命仅为160 a。另外总体来看构件的疲劳寿命远大于设计基准期100 a，因此该桥钢桁构件在服役期内具有很高的疲劳可靠度水平，失效概率很低。

4 结论

基于大桥短期的现场监测数据，采用核密度方法获得日等效应力Seq和日循环次数的概率密度函数，然后利用Monte-Carlo法获得构件细节处的时变疲劳可靠度指标曲线，得到了如下结论：

(1)当车辆荷载经过构件上方时外侧斜腹杆所受的拉应力最大，相对其他杆件更容易发生疲劳破坏，因此应当得到高度关注。

(2)当样本数据较少时，可采用核密度方法获得更合理的样本概率分布模型，进而有效地进行大桥疲劳可靠度评估分析，该方法可为相关研究提供参考。

(3)该大跨钢桁悬索桥钢桁主梁构件在设计基准期内具备较高的疲劳可靠度指标，疲劳失效概率很低，但车流量的增长会急剧地降低构件细节处的疲劳寿命，因此应当时常监控车流量的增长和车轴重的增长情况。