温差作用下外贴FRP加固混凝土桥梁界面黏结性能研究

2020-05-19郝建文李汉江郭海燕蒋济同

公路交通科技 2020年4期

董坤，郝建文，李汉江，郭海燕，蒋济同

(1. 中国海洋大学工程学院，山东青岛 266100； 2. 滨州公路养护处，山东滨州 256600)

0 引言

外贴纤维增强聚合物(FRP)材料加固混凝土桥梁结构的施工技术因其施工方便，并充分利用FRP材料自身轻质高强的优点，已成功用于国内量大面广的中小跨径混凝土桥梁的加固修复工程[1-3]。对于外贴FRP加固混凝土桥梁结构，通常使用胶粘剂将FRP材料与混凝土粘合在一起，从而保证FRP材料与混凝土之间力的传递。因此，FRP材料与混凝土之间黏结性能的强弱对加固效果具有重要影响。由于胶粘剂及FRP材料性能的差异性，FRP-混凝土界面黏结-滑移本构也相差较大，国内外学者在结合试验和理论研究的基础上提出了较为准确的黏结-滑移行为预测公式[4-7]。然而，由于FRP材料与混凝土的线膨胀系数相差较大，在温差作用下，界面黏结层会产生温度应力，而温度应力则对界面黏结性能产生一定的影响。尚守平[8]通过对FRP材料加固后桥梁进行现场实地的长期监测，系统地测出随着温差的变化，加固结构的黏结界面真实存在着一定的温度应力。因此，明确温度应力对界面黏结性能的影响，给出考虑材料和界面参数变化的理论计算公式，是对处于较大环境温差下结构进行加固设计时的关键。

现有文献中关于温度下FRP-混凝土界面黏结性能的理论研究很少。部分学者结合试验和对常温理论的修正提出了一些简化的温度下界面黏结性能模型。Dai[9]在双参数黏结-滑移本构模型的基础上，考虑了温度对FRP材料性能以及胶粘剂黏结性能的影响，提出了温度下的界面非线性黏结-滑移模型；Gamage等[10]在试验研究基础上提出了简化的三线性FRP-混凝土界面剪切强度随温度变化公式；Caggiano. A[11]采用基于断裂能的弹塑性界面模型，提出了高温下FRP-混凝土界面黏结-滑移性能的热力学模型。但上述学者对温度下界面黏结性能的研究中，并未明确给出界面温度应力的分布及退化规律。在针对界面温度应力的研究中，赵启林[12]提出了一种弹性计算方法推导FRP加固梁的界面温度应力；黄龙男[13]、于天来[14]等也同样推导了温差作用下界面温度应力的定量公式，同时指出了界面温度应力的分布及大小与FRP材料的刚度和温差有较大关系，而被补强基底材料的刚度对界面温度应力几乎没有影响；张路[15]分析了因日照辐射和均匀变温引起CFRP加固混凝土箱梁的温度自应力。但上述理论研究中，均忽略了界面滑移对于温度应力的影响，这种假定显然是与实际不相符的。同时，忽略滑移会加剧端部应力集中现象，这会高估界面温度应力对于界面黏结性能的影响，使加固设计存在一定的不合理性，故温度应力的计算应充分考虑滑移效应对端部应力的释放。

本研究考虑界面滑移，引入材料变量和双线性黏结-滑移界面本构模型，解析推导了温差作用下FRP-混凝土界面受力全过程中界面滑移、黏结应力分布和FRP材料应力应变的计算公式，并结合试验数据和数值模拟验证了解析式的正确性。随后，利用解析式探究了不同温差作用下温度应力的分布及变化规律，并分析了温差和黏结层数对界面性能的影响。

1 考虑界面滑移的温度应力求解

1.1 温差作用下界面微分方程建立

本研究采用双线性黏结-滑移本构模型进行温度应力的解析推导，本构模型如图1所示。双线性黏结-滑移本构由式(1)描述，其中界面模型的主要控制参数有3个：界面剪应力峰值τf、界面剪应力峰值对应的滑移量s1、极限滑移量sf。

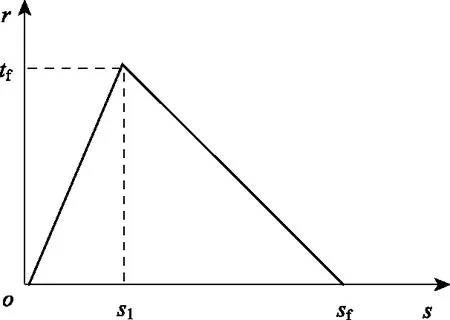
图1 本构双线性模型Fig.1 Bilinear constitutive model

(1)

在温差作用下FRP-混凝土黏结界面的响应以黏结中心为原点呈对称分布，对称位置的界面滑移、黏结剪应力、FRP应力应变等量均数值相等，大小相反。因此，此处取一半节点进行受力分析，黏结节点分析模型及典型微元如图2、图3所示。根据材料的弹性模量及厚度的相对关系，分析过程中做了如下假定：

(1)界面树脂只承受剪应力，而不承担正应力，且不考虑温度变化引起的蠕变；

(2)FRP材料所受正应力沿厚度方向均匀分布，且不考虑宽度方向的应力变化。

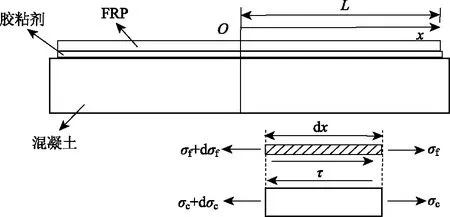
图2 温差作用下黏结节点模型Fig.2 Model of bond joint under temperature difference

根据图2中黏结节点的受力情况，存在以下平衡方程：

(2)

σftfbf+σctcbc=0，

(3)

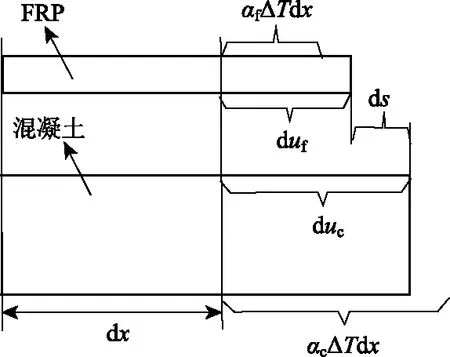
图3 温差作用下微元体变形图Fig.3 Microelement deformation under temperature difference

式中，σf为FRP应力；σc为混凝土应力；tf为FRP厚度；tc为混凝土厚度；bc为混凝土宽度；bf为FRP宽度；τ为界面黏结剪应力。

温差作用下，微元体变形如图3所示。结合工程应用中多数的实际情况(αc>αf,ΔT>0)得：

σf=Ef(εf-αfΔT)，

(4)

σc=Ec(αcΔT-εc)，

(5)

s=uc-uf，

(6)

式中，αf和αc分别为FRP和混凝土线膨胀系数；εf和εc分别为FRP和混凝土的轴向应变；Ef和Ec分别为FRP和混凝土弹性模量；ΔT为界面温差；s为界面滑移量；uf和uc分别为FRP和混凝土的变形量。

联立式(3)～(6)可得：

(7)

(8)

联立式(1)～(8)，同时引入界面断裂能Gf，可得界面滑移的微分平衡方程：

(9)

(10)

1.2 界面微分方程求解

由界面理论预测可知：在温差作用下，界面黏结中点处滑移始终为0，伴随脱粘过程的开始到脱粘极限状态下，在黏结中点两侧处的一定范围内始终存在着弹性应力增长阶段。因此，随着温差的增大下界面黏结-滑移行为只可能出现3个阶段，即弹性阶段、弹性-软化阶段和弹性-软化-脱粘阶段，如图4所示。图4中a为界面软化长度；ad为界面脱粘出现时的软化长度；d为界面脱粘长度。

图4 温差作用下界面剪应力分布和脱粘开展Fig.4 Interfacial shear stress distribution and debonding under temperature difference

1.2.1 弹性段求解

温差不大时，在整个界面长度内都将处于应力弹性增长阶段，即在黏结端部x=L处，界面黏结剪应力τ小于τf，界面滑移s小于s1，如图4(a)所示。将本构关系代入式(9)中，可得如下微分方程：

(11)

(12)

式中λ1，λ2,λ均为常系数。

由温差作用下黏结节点受力情况可确定微分方程式(11)的边界条件为：

(13)

将边界条件式(13)代入式(11)中，解得：

(14)

(15)

(16)

(17)

现将x=L处(黏结端部)滑移用Δ表示，温差-端部滑移关系式可由式(14)得到：

(18)

1.2.2 弹性-软化段求解

随着温差继续增加，滑移增大， FRP-混凝土材料的界面进入弹性-软化阶段，如图4(c)所示。将本构关系代入式(9)中，可得如下微分方程：

(19)

(20)

(21)

此时的边界条件为：

(22)

将边界条件式(22)代入微分方程式(19)、式(20)得：

弹性区域(0≤s≤s1，即0≤x≤L-a)的解：

(23)

(24)

(25)

(26)

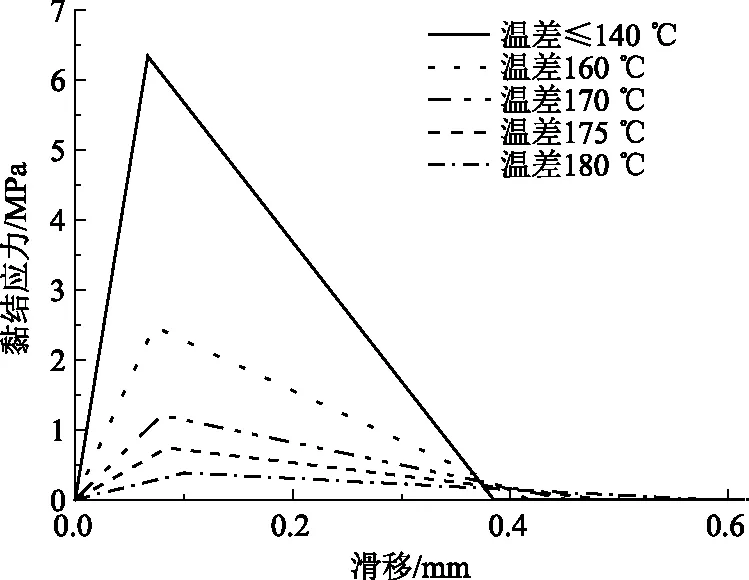
软化区域(s1

(27)

(28)

(29)

λ2cos[λ2(x-L+a)]}〉。

(30)

由式(27)可得，弹性-软化阶段温差-端部滑移关系式为：

(31)

在x=L-a处，将s=s1代入式(23)可得温差与软化长度a的关系：

(32)

1.2.3 弹性-软化-脱粘段求解

温差继续增加，随着界面软化程度的加深，界面将出现脱粘并且沿着界面由黏结端部向黏结中点处开展。由此，通过脱粘出现时，如图4(d)所示，令Δ=sf这一条件得到脱粘出现时的软化长度ad，即式(33)：

(33)

在脱粘出现后，随着温差继续增加，脱粘将继续扩展。脱粘发展的过程如图4(e)所示，通过引入脱粘长度d，用(L-d)代替弹性-软化段解析公式中的L，式(23)～式(30)仍旧成立。

此时，温差-端部滑移关系可改写为：

Δ=sf+(αc-αf)ΔTd。

(34)

在x=L-d处，界面黏结剪应力τ=0，由此得到软化长度a、脱粘长度d与温差ΔT之间的关系式：

(35)

2 温度应力解析表达式验证

运用上述解析表达式与已有试验数据进行对比分析，同时对试验工况进行数值模拟，用以验证解析表达式的正确性。

2.1 试验和数值模型概况

对比试验选用哈尔滨工业大学黄龙男等[13]对FRP补强混凝土梁界面进行的温度应力试验，同时制作了无约束的FRP单向复合材料试件，用以测定FRP复合材料的线膨胀系数。FRP补强混凝土梁试件尺寸见图5，试验所用碳纤维片材、胶粘剂和混凝土材料性能及尺寸见表1，其中胶粘剂的玻璃化温度Tg为180 ℃，混凝土圆柱体28 d强度51.2 MPa。

表1 试件材料基本信息Tab.1 Basic information of test materials

试验时设定基准温度为20 ℃，测试温度分别为-15，40，60 ℃。根据文献[16-17]中对高温作用下胶粘剂试验研究结果可知，胶粘剂性能的变化区间在其玻璃化转变温度Tg±20 ℃的范围内，故可认为在此试验中的界面黏结-滑移本构模型不随温度发生改变。根据Yuan[18]和Dai[19]的建议公式，界面参数取为τmax=6.334，s1=0.066 6，sf=0.384 6。

利用有限元软件Abaqus对文献[13]的试验进行了数值模拟，模型尺寸如图5所示，其中，混凝土材料采用实体单元C3D8R，FRP材料采用3维壳单元S4R模拟；FRP材料与混凝土界面的黏结-滑移关系采用Connector单元模拟。

图5 FRP加固混凝土试件(单位：mm)Fig.5 FRP strengthened concrete specimen (unit:mm)

2.2 结果对比验证

针对剪应力引起的应变分布，即ds/dx，图6给出了试验、解析式以及数值模拟的对比。从图6(a)中可以看出解析式、数值模拟与试验结果3者间的良好吻合；同时，图6(b)中给出了试验与解析解两者间具有良好的相关性，相关系数为0.982 4，标准误差为0.000 036，验证了解析表达式的正确性。

图6 解析表达式的对比验证Fig.6 Comparison and verification of analytic expressions

图7给出了试验工况下，FRP应力分布和界面黏结剪应力分布的数值结果与解析结果的对比。从对比结果来看，数值结果与解析结果吻合良好。其中，FRP应力在黏结中点处最大，沿长度方向向黏结端部减小，在端部处的应力为0；界面滑移在黏结中点处为0，沿长度方向向黏结端部呈非线性弹性增长。同时，数值结果中黏结中点界面滑移与黏结端部处的FRP应力结果，验证了解析推导中边界条件的正确性。

图7 试验工况解析式与数值模拟结果对比Fig.7 Comparison of result obtained from numerical simulation and Analytical formula of test condition

3 温差和黏结层数对界面性能的影响

3.1 不同温差对界面性能的影响

在常温下界面本构的参数不会发生变化；而随着温度升高，胶粘剂软化，界面本构的参数也将产生变化。根据文献[20]中的断裂能等效原则，可计算出双线性本构关系随温度变化规律，图8给出了各温差下界面黏结-滑移模型。

图8 不同温差下界面黏结-滑移模型Fig.8 Bond-slip model at different temperature differences

图9给出了温差变化下界面黏结剪应力和滑移的分布图。由图9(a)可知，界面滑移随着温差的增大而增大。在温度未进入胶粘剂玻璃化转变温度区间时，界面滑移始终很小，且只有在距离黏结端部30 mm左右范围内出现明显滑移，其余位置几乎无明显变化，同时由图9(c)可得，此时端部滑移值与温差增长间的斜率较小；而在温度进入胶粘剂玻璃化转变温度区间时，界面滑移变化开始明显加快，并且端部滑移值与温差增长间的斜率陡然增大，黏结端部出现界面软化。当温差达到180 ℃(温度Tg+20 ℃)时，界面滑移分布已接近呈线性分布。

图9 不同温差对界面黏结性能的影响Fig.9 Influence of different temperature differences on interface bonding behavior

由图9(b)可知，在温度未进入胶粘剂玻璃化转变温度区间时，随着温差的增大，界面黏结剪应力随之增大；当在温度进入胶粘剂玻璃化转变温度区间时，随着温差的增大，界面最大黏结剪应力开始下降。在温差170 ℃时，界面黏结剪应力分布出现下降点，意味着界面端部出现软化；继续升温，黏结剪应力下降点向黏结中点处靠近，意味着端部软化程度的加深。同时，由图9(c)可得，在温差140 ℃时，界面黏结剪应力最大值达到峰值；而当温差达到温差180 ℃时，因界面软化加深，界面黏结强度退化为峰值的10%。

同时，试验中采用的FRP材料加固混凝土的界面剪切强度为6.4 MPa。而在温差作用下界面黏结剪应力最大值达到3.3 MPa，其值达到了FRP材料加固混凝土的界面剪切强度的51%。因此，温差产生的界面温度应力会对加固梁界面黏结性能产生相当不利的影响。

3.2 黏结层数对界面性能的影响

FRP黏结层数变化所影响的是黏结层的刚度，结合Dai[19]给出的界面断裂能计算公式和文献[20]中的断裂能等效原则，可计算出双线性本构模型随黏结层数的变化规律，图10给出了不同黏结层数下的界面黏结-滑移模型。

图10 不同黏结层数下界面黏结滑移-模型Fig.10 Bond-slip models with different bonding layers

图11给出了两种温差下不同黏结层数的界面滑移和黏结剪应力分布图。结合图11可得：当温度未进入胶粘剂玻璃化转变温度区时，随着黏结层数的增加，界面滑移和黏结剪应力均呈现出增大趋势。但整个界面长度内均处于非线性的弹性增长阶段，界面间未因增加黏结层数而出现界面的软化。可见，此时增加黏结层数可以提高加固效果。

图11 温差60 ℃和160 ℃下不同黏结层数界面物理量分布Fig.11 Distribution of interfacial physical quantities of different bond Layers at temperature difference of 60 ℃ and 160 ℃

当温度进入胶粘剂玻璃化转变温度区时，由图11可知，随着黏结层数的增长，界面滑移数值大幅度提高。界面黏结剪应力则仅在黏结层数为1层时，整个界面长度内均处于非线性的弹性增长阶段；而在加固层数为2，3，4层界面黏结剪应力分布出现了下降点，且最大黏结剪应力均小于1层时的最大黏结剪应力，即界面进入了软化脱粘阶段。可见，此时增加黏结层数会加快界面软化的出现。