运营期上硬下软型双层地基动力损伤评价

2020-05-19曹海莹

公路交通科技 2020年4期

曹海莹，杜量，徐珊

(1. 燕山大学建筑工程与力学学院,河北秦皇岛 066004；2. 燕山大学河北省土木工程绿色建造与智能运维重点实验室，河北秦皇岛 066004)

0 引言

由于水分蒸发、盐分沉积和地下水位变幅等原因，在我国沿海和平原地区广泛分布着一层硬度较大的土层，称之为硬壳层。由于上硬下软型双层地基(简称双层地基)存在具有一定承载能力的硬壳层，一直备受国内外学者的关注[1-2]。文献[3]详细阐述了路基中硬壳层的工程特性，并展望了天然硬壳层的利用前景。利用天然硬壳层作为路基持力层，可以节省地基处理的费用，利于优化工程设计。为了降低硬壳层承担荷载的风险，往往采用低路堤设计方案，这导致了车辆荷载作用下传递至路基土动应力的增加，加大了路基运营期失稳的风险性。因此，运营期双层地基动力特性与工程设计方面仍有诸多问题亟待解决。由于土体动力学性质的复杂性和车辆荷载的随机性等因素制约[4]，相关研究鲜有报道。

目前，关于车辆荷载作用下路基土动力学特性的研究正处于活跃期，许多学者的努力正在使该领域的成果不断完善和发展。文献[5-6]开展路基土动应力现场监测工作，收集了宝贵的实测数据，但是因投入的人力、物力大，数据量还未积累到一定规模。文献[7-9]分别通过室内动三轴试验、空心圆柱扭剪仪试验和扫描电镜试验，得到了土体动力特性和微观演化特征方面的有益结论，由于采集的土样离散性较大，相关结论尚未达成一致共识。文献[10]构建了车辆-路面-路基相互作用的动力学模型。文献[11]基于动力互易定理推导出移动荷载作用下的土体振动解析解。文献[12] 利用累积孔压模型展开了交通荷载作用下的地基沉降计算，鉴于理论解具有前提假定，需结合具体工况进行应用。文献[13]借助数值模拟手段再现了车辆运动过程中的加、卸载过程。文献[14]计算得到路基土中动应力、动应变的时程变化曲线，而参数大小和模型选择是困扰计算精度的关键因素，其结果仍需结合实际工程进一步验证。

文献[15]研究表明，车辆荷载作用于低路堤时，动应力的有效影响深度范围为2.5～6.0 m，而硬壳层的厚度一般为1.0～5.0 m之间，这说明下卧软土层也被纳入路基土的实际工作区之内，因此，研究运营期双层地基的受力状态至少需要考虑硬、软两个土层。研究层状路基传力特性的代表性方法包括：文献[16-17]采用弹性层状体系理论及传递矩阵法计算动应力传递；文献[18]应用薄层法分析弹性波在层状介质中的传播规律；文献[19]通过数值积分算法获得了成层地基动应力的简化计算方法等，而以上方法并未考虑土层界面处动应力非连续的情况。文献[20-21]分别借助室内模型试验和有限差分法曾验证上硬下软型土层结构在界面处存在动应力突变现象，因此，已有计算手段并不适用于运营期双层地基的情况，相关研究工作仍有待现场监测数据的支撑和理论方法的改进。

本研究在前人研究的基础上，以河北省境内的邢台-临西高速公路(以下简称邢临高速)双层地基为研究对象，基于现场监测数据提出硬、软土层界面处动应力突变的表征参数；结合室内动三轴试验结果和非线性疲劳损伤累计模型，构建硬、软土体关联性损伤变量和双层地基动力损伤演化方程；借助数据统计手段，对地基土损伤演化信息进行挖掘，给出运营期双层地基设计的指标依据。

1 现场监测

1.1 监测方案

邢临高速公路分两期建设，一期工程邢台市至威县段于2003年7月28日开工建设，二期工程威县至山东界段于2004年5月28日开工，2005年12月21日两期同步建成通车。设计标准为：双向四车道、全封闭、全立交高速公路，全长104.64 km，路基宽26 m，设计行车速度100 km/h。低路堤路段路堤高度约2 m左右，最大路堤高度可达到7～9 m。主要路面结构形式：综合稳定土底基层、水泥稳定碎石基层、中粒式沥青混凝土下面层和中面层、细粒式沥青混凝土上面层。

邢临高速分布着典型的双层地基土，硬壳层厚度为1.5～4.1 m，主要分布在K33+550～K39+990和K51+550～K60+455区段。对于天然硬壳层作为路基持力层的路段而言，如果增加路堤高度，路堤可近似作为硬壳层的一部分，对动应力扩散起到关键作用。与此同时，路堤荷载的增加势必会加剧硬壳层的承载负担，如果降低路堤高度，会导致车辆荷载产生的动应力传递到更深的地基土中，进而对道路的运营状况和受力状态产生不利影响。经过前期试验路段的摸索，将K33+550～K39+990和K51+550～K60+455区段采用低路堤方案，路堤高度定为2 m左右。共选择14个典型监控断面，采用螺旋钻孔辅助自制夹具的方法埋置动态土压力盒(XHZ-4XX型电阻应变式)，对硬、软土层界面处的动应力展开监测。监控断面如下：K33+650，K38+650，K39+990和K51+650共4个监控断面和K39+750～K39+950路段(每隔20 m设置1个监控断面)，土体物理力学参数见表1。

仪器布设见图1，在硬壳层底部和软土层顶部埋设1#和2#动态土压力盒。有效监控断面为12个，监测期为1 a(以运营期伊始为起点)，每隔10 d收集1次监测数据。

1.2 监测数据整理

以K39+770断面为例，对监测数据的处理过程进行说明。该断面路堤填高为2.1 m，为沥青混凝土路面，监测起止日期为2007年6月—2008年6月，其动应力监测数据如图2所示。

图2中每个土压力盒的监测数据获取过程如下：每个断面的监测间歇时间为10 d，每次采集约40～50组数据(即同类型车辆经过该监测断面40～50次，每组数据均对应1条动应力波动曲线，取动应力峰值作为该曲线的代表值)，然后对各组数据中的动应力峰值取平均作为本次监测的数据点(剔除异常数据)。在获取样本时，每次采集数据所针对的车辆荷载类型是相同的，但是同一断面相邻次的车辆荷载类型不同，例如：第1次仅监测大型货车(起始时间)，第2次仅监测中型货车(第10天)，第3次仅监测小轿车(第20天)。

表1 土体物理力学参数Tab.1 Physico-mechanical parameters of soils

图1 监测仪器布设Fig.1 Layout of monitoring instrument

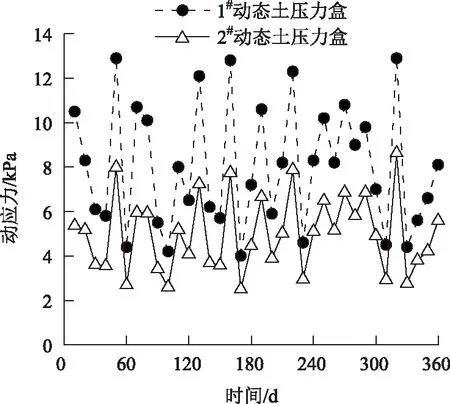
图2 K39+770断面动应力监测数据的平均值Fig.2 Average values of dynamic stress monitoring data (section K39+770)

由图2可知，受到车辆荷载大小、车速变化等多种因素的影响，1#和2#动态土压力盒的监测数据波动性较大，真实反映了车辆荷载作用下土层中动应力的响应特征，符合统计学中抽样随机性的原则。依据文献[20]室内模型试验结果验证和文献[22]理论计算公式的估算，图2中的数据具有可靠性。

定义动应力界面传递系数为ξ，即：

(1)

式中,σd1为硬壳层底部的动应力幅值(1#动态土压力盒；σd2为下卧软土层顶部的动应力幅值(2#动态土压力盒)。

利用式(1)对图2中的原始数据进行处理，计算结果如图3所示。

图3 动应力界面传递系数随时间的变化曲线Fig.3 Curve of dynamic stress interface transfer coefficient vs. time

由图3可以看出，K39+770断面动应力界面传递系数随时间变化曲线具有良好的线性拟合特性，其平均值为0.628(明显小于1.0)，这说明在土层界面处发生了动应力突减现象。这主要是由于上硬、下软两种土体介质的波阻抗具有差异性所导致的，即当车辆荷载产生的应力波传递至土层界面时，反射波的存在使得透射波的能量被消减，进而诱发动应力的突变。由拟合直线的斜率可知，随着交通运营期的增加，动应力界面传递系数的数值略有升高，这说明硬壳层经受车辆荷载长期作用后其力学性能产生了劣化(波阻抗降低)，对动应力的界面突减作用在消弱；而拟合直线的斜率值很小，证明硬壳层的力学性能劣化是一个非常缓慢的过程，如果近似按照图3中拟合直线方程展开预测，当交通运营时间为5.6 a时，动应力界面传递系数ξ=1.0，即硬壳层对动应力的突减作用消失。

依照K39+770断面对监测数据的处理过程，可获得12个断面的动应力传递系数平均值(其他11个断面的传递系数时程曲线同样具有较好的线性拟合特性)，见表2。

表2 动应力界面传递系数平均值Tab.2 Average value of dynamic stress interface transfer coefficient

由表2可知，动应力界面传递系数介于0.4～0.6之间的断面有5个，介于0.6～0.8之间的断面有7个。因此，土层界面处的动应力突减现象是客观存在的(以下简称界面效应)。工程设计中往往假定土体为均质材料，忽视了层状地基的界面效应，显然过高估计了双层地基中的应力水平，致使设计方案过于保守。同时，界面效应的存在有利于低路堤设计方案的实施，对降低路基土动应力水平起到积极作用。

2 室内动三轴试验

为了获得硬、软土体的临界动应力值，采用套筒式土钻分别在硬壳层底部、软土层顶部采集土样，制备出若干试样进行室内动三轴试验，试样尺寸：直径d=39.1 mm，高h=80 mm。试验采用国产SDT-10型微机控制电液伺服动三轴仪，选用的振动波形为正弦波，加载次数为10万次，临界动应力的确定标准为：随着动应力水平的逐级增大，土样的累积应变-加载次数曲线将会呈现出稳定型曲线、临界型曲线、破坏型曲线3种类型，其中临界型曲线对应的动应力为临界动应力[23]。选择围压、振动频率和动应力幅值作为试验控制条件，见表3。

表3 试验条件Tab.3 Experimental condition

图4和图5分别为软土和硬土的临界动应力曲线。

图4 临界动应力Fig.4 Critical dynamic stresses

依照图4，找到临界曲线对应的动应力幅值，即为该土样的临界动应力。经对动三轴试验数据进行统计分析，得到的结果为：硬土的临界动应力范围为50～75 kPa，软土的临界动应力范围为9～21 kPa。

3 运营期路基土损伤评价

由于高速公路的设计使用年限一般为15～20 a，在运营期内路基土承受车辆荷载作用达几千万次，属于典型的低应力水平诱发高周疲劳破坏情况，路基土的力学性能由原状土逐渐演变为损伤土。从这个认知角度出发，引入路基土损伤评价机制能够有效反映路基土的运营状况和受力状态。

3.1 损伤演化方程构建

文献[24]应用的Richart-Newmark模型(简称R-N模型)，是一种非线性疲劳损伤累计模型。该模型能够有效地考虑荷载幅值和加载次序对材料变形损伤的影响，不仅适用于高周疲劳条件，且还能很好地反映岩土工程材料的非线性变形特征。但是R-N模型以往的应用对象往往为单一土体，为便于双层地基土体的损伤评价，将其拓展为包含硬、软两种土体的整体损伤演化方程，如式(2)所示：

(2)

式中，Dmi为前m个车载序列引起的总土体损伤值，无量纲；nm为第m个车载序列的加载次数；Nm为动应力幅值σdi作用下的土体临界循环次数；cmi为与土体动应力水平相关的计算参数，无量纲；i代表土体的类型，即：当i=1时表示硬土，当i=2时表示软土。

兼顾双层地基土的动力学特点和cmi值的属性，构建如下cmi值的计算公式：

(3)

(4)

式中，σdcri为土体的临界动应力；σdi为土体中的动应力幅值；Si为土体的动应力水平。

(1)当σdi=0时，cmi=1，此时式(2)演变成P-M线性损伤累积模型；

(2)当0<σdi<σdcri时，0

(3)当σdi=σdcri时，cmi=0，Dmi=1，此时土体处于完全损伤状态。

3.2 两种土体计算参数的关联性

定义λ为硬、软土体的动应力水平关联性系数(同一车辆荷载作用下)：

(5)

式中，S1为硬土的动应力水平；S2为软土的动应力水平。

将式(1)和式(4)代入式(5)，可得：

(6)

式中，σdcr1为硬土的临界动应力；σdcr2为软土的临界动应力。

由式(6)可知，界面动应力传递系数ξ与土体临界动应力比σdcr1/σdcr2均可表现硬、软土动力特性的差异性，但两者的变化趋势正好相反。将表1中的12组现场实测ξ值及临界动应力的试验结果代入式(6)，得到λ=1.60～1.73，λ值在一个很小的范围内波动，其波动误差不超过6.25%，说明硬、软土的动应力水平具有较强的关联性。

将式(5)代入式(3)可得：

cm2=1-λ(1-cm1)，

(7)

式中，cm1为硬土损伤模型的计算参数；cm2为软土损伤模型的计算参数。

利用式(7)可以得到硬、软土模型计算参数之间的关系曲线，如图5所示。两种参数取值范围局限于两条边界线之内，可见两者也具有较强的相关性。

图5 R-N损伤模型参数关联曲线Fig.5 Relevance curves of R-N damage model’s parameters

3.3 硬、软土体损伤演化特征

为得到高速公路准确的加载情况，需要对车辆载荷谱进行统计分析。为研究方便，分别以100%轻型车辆作用、80%轻型车辆+20%重型车辆作用(以下简称轻载作用为主)、50%轻型车辆+50%重型车辆作用、20%轻型车辆+80%重型车辆作用(以下简称重载作用为主)4种工况展开计算，其中20%，50%，80%和100%指加载车辆出现的概率。以K39+870断面和K38+650断面为例，其R-N模型计算参数见表4，土体损伤曲线如图6所示。

表4 R-N损伤模型计算参数Tab.4 Calculation parameters of R-N damage model

图6 土体损伤曲线Fig.6 Curves of soil damage

定义硬、软土损伤曲线在原点处切线之间的夹角为θ(以下简称夹角)，该夹角的数值变化可分解为两部分：数值不变而位置发生转动，以及位置不变而数值发生改变。将第1部分转动的角度用β表示(以下简称夹角转动)，将第2部分数值的改变量用Δθ表示(以下简称夹角增量)。将图7导入CAD软件中，借助CAD软件的绘图和测量功能，可以较为便捷地获取到夹角θ和夹角转动β的数值大小。在图7中只需将各损伤曲线与损伤值Dmi=1对应的直线取交点，该交点的横坐标即为运营期寿命的数值大小。

图7 硬、软土运营期寿命的统计关系Fig.7 Statistical relation between operation period lives of hard soil and soft soil

由图7可知，对于K38+650断面而言，轻载作用为主时夹角θ1=32.2°，重载作用为主时夹角θ2=41.5°，θ2相对θ1绕原点逆时针发生夹角转动β=8.8°，同时产生夹角增量Δθ=9.3°；对于K39+870断面而言，轻载作用为主时夹角θ3=35.1°，重载作用为主时夹角θ4=39.2°，θ4相对θ3绕原点逆时针发生夹角转动β=9.8°，同时产生夹角增量Δθ=4.1°。K38+650断面、K39+870断面的夹角转动β和夹角增量Δθ均未超过10°，但是两者的运营期寿命(当Dmi=1时对应的加载次数)降低值却相差很大，前者降低4 200万次，后者降低2 700万次。可见，夹角转动β与夹角增量Δθ对路基运营期寿命十分敏感，是评价路基损伤的两个关键指标(其他10个断面的计算结果也得出了相似结论)。

值得关注的是，在不考虑界面效应且轻载作用为主时，软土的运营期寿命为8 700万次(图7(a))和3 500万次(图7(b))；在不考虑界面效应且重载作用为主时，软土的运营期寿命仅为3 800万次(图7(a))和0次(图7(b))。计算结果与工程实际严重不符，这说明双层地基设计中不能忽视界面效应的影响。

4 工程设计指导

夹角转动β、夹角增量Δθ及运营期寿命用来表征土体损伤演化特征比较直观，但用于工程设计中操作性不强，下面对12个断面的土体损伤曲线信息进行统计分析。

4.1 路基失稳关键层的确定

分别以硬、软土的运营期寿命为横、纵坐标建立坐标系，如图7所示。

由图7可知，所有数据点均在y=x直线的下方，说明在相同工况下软土的运营期寿命短于硬土，即软土的损伤程度大于硬土，路基的总体运营期寿命取决于软土层，软土层是控制路基稳定性的关键土层，这与文献[25]的结论基本一致。由式(6)的计算结果不难得出，这是软土动应力水平均高于硬土所导致的结果。

由于下卧软土层并不位于地表，且车辆荷载传递至此的动应力数值很小，其潜在的破坏行为和对路基稳定性的影响程度往往被忽视，这一点在双层地基设计中应引起高度重视。

4.2 车辆荷载增幅影响

以100%轻型车辆作用为基准，将12个断面其他3种工况产生的夹角转动β最大值、最小值与荷载增幅(例如，轻载作用为主较100%轻型车辆作用的荷载增幅为40%)绘制在同一个坐标系，如图8所示。

图8 夹角转动与荷载增幅的拟合曲线Fig.8 Fitting curves of intersection angle rotation and load increment

由图8可知，夹角转动β与荷载增幅之间基本呈线性关系，说明夹角转动β主要受车辆荷载大小影响，车辆荷载加大时β为逆时针，反之为顺时针。车辆荷载每增幅10%夹角转动β相应增加约1°，运营期寿命降低约270～480万次，这为估算超载运营工况的双层地基寿命提供了依据。

此外，从图8的两类数据点分布特征看，轻载作用为主的数据区域向重载作用为主的数据区域发生了逆时针偏转，这说明车辆荷载的增加使得软土层的运营期寿命缩短速度快于硬土，导致整个路基的运营期寿命呈现加速降低的趋势。

4.3 硬壳层厚度的利用范围

由于传递路径的增加，硬壳层厚度直接影响到车辆荷载传递至软土层的动应力大小，继而影响到软土的运营期寿命。将12个断面的硬壳层厚度与对应的软土层运营期寿命(包括轻载作用为主和重载作用为主两种工况)建立在同一坐标系下，如图9所示。

图9 硬壳层厚度与软土运营期寿命关系曲线Fig.9 Curves of hard crust’s thickness vs. soft soil’s operation period life

由图9可知，两种工况下的关系曲线基本呈上升走势，即随着硬壳层厚度的增加，软土运营期寿命得以延长。重载作用为主工况下曲线相对平缓，主要是由于重载交通导致硬壳层性能劣化严重，界面效应减弱明显，致使传递至软土层中动应力增加，与硬壳层厚度增加引发动应力减小两者呈抵消之势。

在开始阶段两条曲线趋于平缓，并出现了小幅波动，这主要是因为硬壳层厚度较小，承载能力相对薄弱，其力学性能劣化明显，导致上述动应力抵消现象显著造成的。找出两条曲线共有的稳定上升段起点，对应的硬壳层厚度为2.3 m，该数值可以作为高速公路工程设计中的重要参考值。

4.4 硬、软土压缩模量比拐点值

图10 夹角增量平均值与压缩模量比的拟合曲线Fig.10 Fitting curve of average intersection angle increment and compression modulus ratio

经过10余年的通车检验，发现在利用天然硬壳层作为路基持力层的路段中，其硬壳层厚度超过2.3 m 且硬、软土体压缩模量比大于4.6的断面，其路面出现明显裂缝、车辙的情况很少，且路基监控断面的沉降量未超过预先设定的报警值。2013年7月至8月对重载交通作用较为频繁的上覆厚硬壳层软土路基段展开现场调查，结果表明，5%的区段运营效果较差或一般，15%的区段运营效果较好，80%的区段运营效果优良。

因此，对于同时满足上述两个条件的高速公路路基断面，建议在工程设计中应优先考虑利用天然硬壳层作为路基持力层，而非直接采用地基处理的方式(具体设计时也要兼顾路堤高度、硬壳层刚度等因素的影响)。