递归算法的应用与分析

倪锦园 张建勋

摘  要：递归思想是算法分析设计中最重要的思想之一，递归算法应用十分广泛，借助递归算法可以把一些较为复杂的问题简洁地表示出来。该文重点介绍了递归算法的概念和三个特点，通过计算机博弈树详细说明了递归算法在数据结构中树的应用，使用点格棋博弈过程落子的不同状况系统地介绍了递归算法在图的应用，并通过对照实验重点分析了递归算法和递归算法非递归化的执行效率。

关键词：递归;算法;非递归化;效率

中图分类号：TP301.6        文献标识码：A 文章编号：2096-4706（2020）20-0146-04

Application and Analysis of Recursive Algorithm

NI Jinyuan，ZHANG Jianxun

（College of Computer Science and Engineering，Chongqing University of Technology，Chongqing  400054，China）

Abstract：Recursive thought is one of the most important thoughts in algorithm analysis and design. Recursive algorithms are widely used. With the help of recursive algorithms，some more complex problems can be expressed concisely. This article focuses on the concept and three characteristics of the recursive algorithm. This paper describes the application of recursive algorithm in data structure tree in detail through computer game tree，systematically introduces the application of recursive algorithm in graph by using different situations in the process of point chess game，and analyzes the execution efficiency of recursive algorithm and recursive algorithm non recursive through contrast experiments.

Keywords：recursion;algorithm;non-recursive;efficiency

0  引  言

在日常編程过程中，通过使用递归算法可以简化大量的代码，同时也让代码的可维护性变得更好。笔者通过将递归算法应用到点格棋博弈系统中，完成了整个博弈系统搜索引擎和测试引擎的实现，并在全国计算机博弈大赛上取得了较好的成绩。递归算法是程序开发过程中一种重要的方法，通过递归算法可以让程序的结构性更加清晰，可以把一些不容易解决的问题处理好，而且解题思路更为明确，不容易产生歧义。在算法分析与设计课程中很多问题都用到了递归的方法，比如汉诺塔问题、整数划分问题、求阶层问题等。递归算法的设计还是比较复杂的，要设计一个好的递归算法来解决以上问题就要注意三个关键点：首先分析问题的定义，找到合理的解决办法就需要找出算法的递归公式，设计一个好的递归公式是解决问题的关键;其次设计一个递归的边界条件也就是递归的终止条件是十分重要的;最后的关键是要不断地缩小问题的规模，记录递归时参数传递的过程[1，2]。

1  递归算法概述

1.1  递归算法概念

递归算法是指算法本身可以直接或者间接的调用自己，将一个较为复杂的问题分解为规模较小的子问题，算法在执行过程中重复不断地实现自我调用的过程。在不断递归调用的过程中，只有达到递归边界的临界值时，才会跳出递归循环，递归算法会从后往前依次逆序返回，就是把每一层递归调用的值放入一个栈中，算法执行到递归的出口时，就进行出栈的操作，从最后一层递归调用的值逆序返回，返回到第一个入栈操作，这样就完成了整个递归算法的操作[3-5]。

1.2  递归算法特点

递归算法在程序设计中是十分重要的方法，帮助解决了许多较为复杂的问题，递归算法极大地简化了程序开发的工作量，使程序的结构性也较为清晰，可读性更高，同时让问题更容易被理解和接纳。递归算法主要有下面三个特点。

1.2.1  设计递归公式

递归算法直接或间接的调用自己本身，将一个较为复杂的问题化解为一个或多个子问题来求解，同时子问题与被分解的问题有同样的算法，举个简单的例子递归求n个元素的和，可以写出公式f（n）=n+f（n-1）进行递归迭代，还有比较经典的汉诺塔问题，就是以c柱为支撑柱，将a柱上n-1的盘子移动到b柱上的公式是f（n-1，a，c，b），移动的盘子打印输出move（n，a，c）;以a柱为支撑柱，将b柱上的盘子移动到c柱的公式是f（n-1，b，a，c）。每一次迭代递归的时候，问题规模都在缩小，同时上一次的输出成为了下一次迭代递归的输入。

1.2.2  递归算法的边界条件

边界条件就是递归的出口。递归算法不是无穷无尽的，当程序递归到最后一层时，就要返回输出。由于每一层递归都会使问题规模不断缩小，所以每一次递归都会越来越趋近于终止条件，直到达到终止的条件，返回临界值。例如递归求阶乘问题f（n）=n·f（n-1），递归的终止条件当n=1时，如果没有递归的边界条件，此时程序是无限循环的，没有输出结果。递归算法的边界条件有的时候也不止一个，在整数划分问题里面，要分别讨论最大化分数值和被划分的整数值大小关系，此时递归边界条件也有多个的。

1.2.3  缩小问题的规模

递归过程中需要不断地减小问题地规模，而且递归算法是在直接或间接地调用自身，所以递归时参数传递的过程中，要逐步减少或者增加参数值向递归算法的边界条件靠拢，控制了递归方向才能控制递归算法。例如斐波那契数，F（0）=

0，F（1）=1，F（n）=F（n-1）+F（n-2），每一次递归调用的过程中，问题的规模都在不断地缩小，直到问题规模缩小到递归出口的时候，就达到了递归输出的条件。

2  递归算法的应用

2.1  递归算法在树中的应用

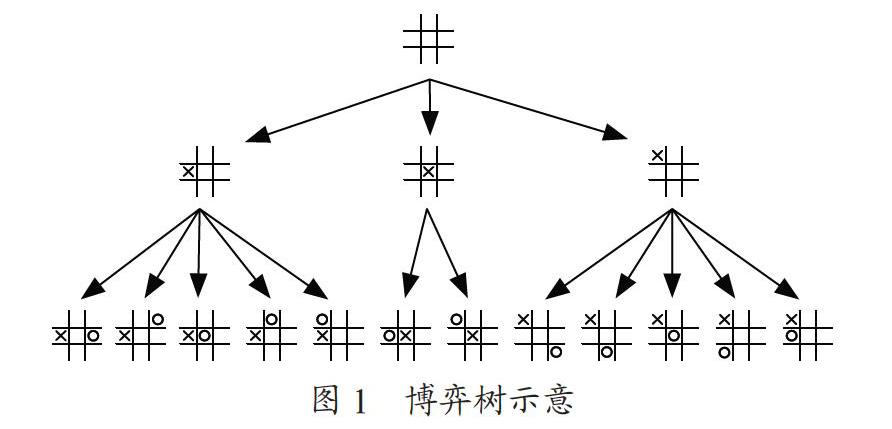
树是一种基本的数据结构，它是由n（n>0）个有限节点组成一个具有层次关系的集合[6，7]。树里面每一个节点具有相同的数据结构，每个数据元素直接的关系是“一对多”，所以很多有关树的问题通常用到递归的思想。本文提到的计算机博弈树也运用了递归的思想，博弈树的每个节点代表一个落子后的一个局面，每个局面都是递归产生的，而且是通过深度优先遍历，一层一层往下延伸，每一个局面生成的过程都会在上一层局面中进行递归搜索，搜索到上一层局面没有落子的位置时，就會产生新的局面，它的根节点也就是现在所处的局面，也成为当前局面。因为双方落子的不确定性，博弈树的递归发展也是不一样的，但总是根据棋盘信息进行模拟递归展开的，然后逐渐地就可以形成一个树形结构。以井字棋为基础的博弈树的示意图如图1所示。在图1中，博弈树主要是通过井字棋来建立的，表现一局井字棋游戏博弈树的全部过程，整颗博弈树构建的过程是通过递归产生的，井字棋游戏是由双方轮流着边的棋类博弈游戏。

在图1中的根节点表示一个空棋盘，根节点下面的三个子节点中的×表示一号玩家可以走的位置，在接下面的一层节点中的○表示的是二号玩家可以走的位置，二号玩家的落子位置完全要根据一号玩家的落子位置，通过递归搜索确定此位置未被一号玩家占领后，才能产生，因此，在棋局的不断进行中，博弈树在每一层递归的过程中也会越来越大。

2.2  递归算法在图中的应用

递归算法在图中的应用是用来描述点格棋先后落子位置顺序的算法，图是由顶点V集和边E集构成，因此图可以表示成G=（V，E），图是一种基本的数据结构，在很多有关于图的应用中都用到了递归算法。点格棋博弈的过程中用到了有关于图的递归算法，点格棋是中国计算机博弈大赛的竞赛项目之一，博弈双方轮流将两个相邻的点连接成一条边，边属于双方共有，只讨论格子的所属，当某一个格子的四条边都被连成线时，占领最后一条边的玩家拥有这个格子，占领格子后有一个奖励边，该玩家必须再下一步。根据这个竞赛规则，可以用递归算法的思想来设计点格棋博弈双方落子的流程图，点格棋递归落子流程图如图2所示。

博弈双方在落子的过程中选择先后手递归进行落子，若电脑先手，电脑进行落子，然后条件判断当前落子是否达到占格的条件，若没有占格，则由玩家进行落子，若都没有达到占格的条件，就递归到另一方进行落子。若任意一方达到占格的条件，则判断当前占格数量是否超过所有格子的一半，若超过一半就跳出循环，若未超过一半就又递归调用自身落子的函数，在点格棋双方博弈的过程中，不断地递归调用落子的函数。

3  递归算法与非递归化

对比递归算法和递归算法的非递归化时，下面就实际操作一个案例来分析各自执行效率，完成任务问题：在一个双线程的电脑上，有n个任务将要完成，完成一个任务都将占用一个线程。一个线程完成任务的方法有两种，可以一次完成一个任务，也可以一次完成两个任务。需要完成n个任务，一共有多少种执行的方法。

用递归思想的具体思路：

（1）当只有一个任务的时候，有一种完成任务的方法。

（2）当只有两个任务的时候，有四种完成任务的方法：分别是两个任务分别占用两个不同的线程，有两种;一个线程一次性完成两个任务，有两种。

完成任务问题的算法实现包括了递归算法和非递归算法。

3.1  递归算法

递归算法在程序执行的过程中，不断地直接或间接的进行自我的调用，递归调用的过程中，系统会为每一层调用开辟新的栈来存储信息，直到程序执行到边界条件的时候，才完成自我调用，然后逆序返回栈中每一层存储的数据，直到把栈里面的数据全部返回，到此就完成了整个递归算法的执行。在解决很多问题的时候，递归算法是十分有效的，它对问题的描述清楚易懂，便于对整个程序的编写和调试。但是递归的过程中需要用到系统的堆栈，会消耗更多的空间资源，当递归深度过于庞大的时候，程序有可能会出现异常死机的现象[8]。完成任务问题的递归算法代码为：

#include

#include

#include

int Digui（int n）

{

if（n==1）        //只有一个任务时，有一种方法

return 1;

if（n==2）

return 4;   //有两个任务时，有四种方法

return Digui（n - 1）+Digui（n - 2）;

}

int main（）

{

long int begin，end;

time（&begin）;

int n;

printf（"请输入任务量：＼n"）;

scanf（"%d"，&n）;

printf（"任务完成的方法一共有：＼n"）;

printf（"%d＼n"， Digui（n））;

time（&end）;

printf（"程序执行过程中的时间：＼n"）;

printf（"%d＼n"，end-begin）;

return 0;

}

3.2  非递归算法

非递归算法执行效率更高，运行时间会随着程序循环的次数增加而增加，没有其他额外调用的开销，非递归算法比递归方法更快，因为非递归方法避免了一些列函数调用和返回中涉及的额外开销，在性能上更具有优势[9，10]。完成任务问题的非递归算法代码为：

#include

#include

#include

int main（）

{

long int begin，end;

time（&begin）;

int x1=1，x2=4;

int n，x;

printf（"请输入任务量：＼n"）;

scanf（"%d＼n"，&n）;

for（int i=3;i<=n;i++）

{

x=x1+x2;

x1=x2;

x2=x;

}

printf（"任务完成的方法一共有：＼n"）;

printf（"%d＼n"，x）;

time（&end）;

printf（"程序执行过程中的时间：＼n"）;

printf（"%d＼n"，end-begin）;

return 0;

}

對照两个实验可以发现：递归算法程序结构简单，易读性更高，程序调试也很方便，但是递归算法依靠栈来实现操作的，不断地在系统内部进出栈，占用了大量的时间和空间，消耗了更多的计算机资源，上述递归算法的时间复杂度O（2n），其中n代表问题的规模。而非递归算法程序结构较为复杂，在编写和调试程序时，会花更多的时间，但因为非递归算法依赖于调用其他函数进行进出栈操作，相对于递归算法来说，消耗了较少的时间和空间。上述非递归算法的时间复杂度O（n）。

当输入任务量为20时，递归算法程序执行时间不到1秒，非递归算法程序执行时间也不到1秒，由此看来，任务量较小的时候，递归算法和非递归算法执行的时间几乎相同。当输入的任务量为40时，递归算法程序执行时间为6秒，非递归算法程序执行时间只有2秒，当任务量较大的时候，递归算法明显比非递归算法更慢。

4  结  论

全文对递归算法进行分析，通过对递归算法的概念和特点进行阐述，然后分别介绍了递归算法在树、图中的应用，接着做了递归算法和非递归算法的对照实验，发现当数据量不够大时，递归算法和非递归算法的时间效率几乎相同，当数据量越来越大时，递归算法的执行时间相比非递归算法来说就越来越慢，递归算法的时间复杂度也要大于非递归算法的时间复杂度，所以递归算法的执行效率更低。因此在实际计算中，还是建议不要大规模使用递归算法。

参考文献：

[1] 宋卫红.数据结构中递归算法的教学研究 [J].现代信息科技，2020，4（13）：188-190+193.

[2] 张耀民.递归算法在程序设计中的应用与分析 [J].电子测试，2013（13）：1-2.

[3] 杨娇.递归思想及其算法设计的探讨 [J].数字通信世界，2018（11）：109+204.

[4] 晏素芹.递归算法的教学方法探讨——以C程序设计为例 [J].福建电脑，2018，34（8）：170-171.

[5] 周世杰.从计算思维的视角辨析算法中的递归与迭代 [J].中国信息技术教育，2020（9）：53-55.

[6] 刘晓静.“数据结构与算法”课程教学改革与实践 [J].微型电脑应用，2015，31（11）：14-17+2.

[7] 张安勤，田秀霞，张挺.数据驱动的数据结构课程案例设计研究与实践 [J].软件工程，2020，23（4）：54-56.

[8] 王爱法，杨梅梅，福春霞.二叉树及其遍历算法的应用 [J].重庆理工大学学报（自然科学），2018，32（11）：194-198.

[9] 肖红德.汉诺塔问题递归算法与非递归算法比较 [J].软件导刊，2018，17（8）：118-120.

[10] 詹泽梅.数据结构中遍历操作的非递归算法 [J].电脑知识与技术，2017，13（28）：40-42.

作者简介：倪锦园（1996—），男，汉族，重庆九龙坡人，硕士，研究方向：数字图像处理与分析;张建勋（1971—），男，汉族，四川乐山人，教授，硕士生导师，CCF专业会员，博士，研究方向：数字图像处理与分析、实时计算机图形学。