树搜索优化算法在FPGA中的应用与实现①
2020-05-18陈建国方振国柏雪婷
陈建国, 方振国,*, 柏雪婷
(1.淮北师范大学物理与电子信息学院,安徽 淮北 235000;2.上海旗升电气有限公司,上海 200000)
0 引 言
科技的发展带动了集成电路集成度的提升,组合逻辑电路是集成电路的重要组成部分,所以对组合电路优化的要求也随之增加。在人工智能技术日驱成熟的环境下,将人工智能在集成电路设计上应用具有光明的前景,而组合电路优化是集成电路优化的基础,所以用人工智能完成组合电路的优化是集成电路发展的又一次突破[1]。组合电路的传统优化算法包括公式法、卡诺图法、Q-M算法,虽然这些算法可以对组合电路进行优化,但它们都有各自的缺点,如公式法化简过程较随机,可能有多个结果,无法判定结果是否为最优解;卡诺图能够快速的化简逻辑表达式,但是当输入变量大于5之后复杂度呈指数上升,且不适合编程;Q-M算法是适用于计算机编程的化简方式并且在前两种方法的问题上有很大的优势,但是每次只能合并一项不同的逻辑表达式,增加了算法的冗余度[2]。人工智能理论应用在硬件当中可以解决很多大规模、复杂度不确定的问题。将人工智能中的树搜索算法进行优化应用在组合电路优化问题中,不仅解决了传统优化算法不易编程、计算量大、冗余度高等问题,而且在多输入变量时优化速度也会大大提升。因此本设计采用树搜索算法优化组合电路并在FPGA上实现,以最小项集合作为树搜索的起始节点,并利用启发式策略向下搜索,搜索完成后叶子节点的集合即组合逻辑电路的最简逻辑表达式[3]。
1 组合电路最小项的概念

表1 五输入一输出真值表
如表1所示,随机选择了一个五输入一输出的组合逻辑电路的真值表,由真值表可以得出输入变量与输出变量之间的逻辑关系。把Y输出为1的项称为最小项,这些最小项的集合,能组成关于Y的逻辑表达式,如下


(1)
2 树搜索优化算法
传统的蒙特卡洛树搜索是通过构造符合一定规则的随机数解决一些数学上的问题,也应用在棋盘游戏与即时电子游戏方面,树搜索过程的每个循环主要包括选择、拓展、仿真、反向传播这四个步骤,从根节点开始在启发式策略下向下搜索,选择合适节点向最优化方向拓展,若搜索到最优解搜索结束,否则向下拓展一个或多个节点,然后从拓展的节点中选择一个进行仿真,即进行随机游戏,最后是反向传播更新随机游戏的结果与路径信息。
树搜索算法在组合电路优化上的应用需要对传统的树搜索算法进行改进,每个循环包括的步骤有优化、选择、拓展、反向传播。将逻辑表达式的最小项集合作为根节点,组合电路逻辑表达式中的每一项设为节点,最简逻辑表达式为树搜索搜索完成后的叶子节点的集合。树搜索在组合电路优化过程的具体过程如下:首先是优化,利用启发式策略优化搜索过程,即搜索同级节点中是否有相同节点,若有合并相同节点,若无进行选择;选择则是按顺序的规则选择节点进行拓展;拓展将节点中的某一项取反(将最小项中的某项字母取反),然后搜索同级节点是否有相同项,若有去除取反字母并拓展为下级节点,若每个字母取反后都无则进入反向传播;反向传播即是把最后的叶子节点反馈,作为组成最简逻辑表达式的一部分。

图1 算法实现树形图
3 算法应用
如图1所示,是表1中的真值表对应组合逻辑电路智能设计的过程,按照树搜索算法实现的树形图,从图1中可以清晰的看到各级节点以及叶子节点的情况[5]。标红的部分是同级节点中已有的相同项,当该节点不是叶子节点时,这些节点往下拓展对应的叶子节点与同级中的相同节点对应的叶子节点相同,相同叶子节点组成的组合电路最简逻辑表达式也是需要合并相同项的,所以同级中的相同节点只需保留一个;同理相同项节点为叶子节点时只需保留一个组成逻辑表达式即可[6]。
以表1对应的真值表为例,逻辑表达式对应为公式(1),算法实现步骤如下:



(2)
4 算法实现
为验证该方案,使用FPGA开发平台进行验证测试,使用Quartus II中的逻辑分析Signal Tap II来观察各级节点数据以及优化结果。首先是真值表的输入,先输入Y,然后对Y进行编码就可以将Y对应的逻辑表达式用二进制数组表示[9]。

图2 编码后的输入(一级节点图)


图3 二级节点结果图
如图3所示和图1中的二级节点相同,这是一轮优化后的结果,g_2是节点数量,generation_2是用来存放二级节点的数组。从图1与图3可得一级节点中只有ABCDE(0000011111b)是叶子节点,ABCDE无法化简,直接赋给最简逻辑表达式数组中的generation[0]如图5所示。当然在这些二级节点中有很多是重复的节点,所以相同项的节点中分别只保留了一个,如图1中标红部分(不进行继续拓展的节点也不是叶子节点)[8]。

图4 三级节点结果图
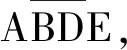

图5 叶子节点
如图5所示,是组合逻辑电路优化过程的结果,也是树搜索过程中合并后的叶子节点的集合,g为优化后逻辑表达式的项数,generation是存放叶子节点的数组,可得化简后的逻辑表达式为式(2),式(2)在功能上等价于最初的(冗长)等式(1)。
对输入进行编码后以二进制代码的形式表示逻辑表达式,在FPGA上更易实现且速度更快,功耗更低[10]。为了验证本算法的效率,分别对传统算法和本文算法进行分析,数据如表2所示。

表2 算法比较
M代表输入量数,N代表最小项个数。
5 结 语
树搜索优化算法应用在组合电路优化方面不仅克服了传统优化算法的不足,也在计算速度上体现了明显的优势,特别是在多输入变量的情况下。树搜索算法优化组合电路在FPGA上的实现与传统算法相比较,证明了该算法具有速度快、空间复杂度低等特点。
